基于抽样学习的关联挖掘算法设计
2018-03-07谢笑盈徐应涛
谢笑盈, 徐应涛, 张 莹
(1.浙江师范大学 经济与管理学院,浙江 金华 321004;2.浙江师范大学 行知学院,浙江 金华 321004;3.浙江师范大学 数理与信息工程学院,浙江 金华 321004)
0 引 言
关联规则[1]是Agarwal于1994年首次提出的、旨在分析购物篮中各商品之间关联性的数据分析方法,该方法能从数据集中找到满足最小支持度(minsup)和最小置信度(minconf)阈值的规则.按照Agarwal的原始提法,要在数据集中提取出关联规则,需要计算每个可能规则的支持度和置信度,这种方法的时空代价太高,因为一个包含d个属性的数据集中能提取的可能规则的个数为r=3d-2d+1+1,若最小支持度为20%,最小置信度为50%,则80%以上的规则将被丢弃,使得大部分的计算是无用的.为了提高挖掘效率,避免进行不必要的计算,统计学界及计算机学界的学者纷纷提出了不同的解决方法.
抽样技术是统计学中常常被用来获取有效信息的经典方法,近十几年来,抽样的方法也开始被许多学者用来提高关联挖掘的效率.这些研究主要包含两大类:一类是静态抽样的方法,即根据数理统计的方法计算出一个能代替总体进行关联分析的样本容量,再用随机抽样的方法抽得该样本;另一类是动态抽样(常分为累进抽样和自适应抽样)的方法,即容量从小到大不断地从总体中抽出样本,同时为抽样设计一个停止抽取的规则,当样本的容量达到抽样停止阈值时,停止抽样,获得的样本被称为最优样本,将作为总体的替代数据集进行关联分析.这种描述样本容量与模型准确度之间关系的曲线称为动态抽样的学习曲线[2],如图1所示.

图1 动态抽样的学习曲线
学习曲线的横轴代表一个样本序列,纵轴代表样本序列对应的准确度值.典型的学习曲线分为3个演变阶段:坡度陡峭阶段、坡度相对平缓阶段和坡度为零阶段.其中,第2和第3阶段的连接点nmin代表的样本容量通常被称为最优样本容量OSS(optimal sample size),对应的样本被称为最优样本OS(optimal sample).因为所有容量大于nmin的样本的准确度不再有显著提升,而所有容量小于nmin的样本的准确度都比它小,所以绘制学习曲线的目的就是要找到nmin,并用它对应的样本完成挖掘任务.要找到nmin并不是容易的事情,就关联挖掘而言,学者们就如何设置高效简便的抽样停止规则做了很多研究,下面就一些有代表性的抽样方法进行综述.
文献[3]设计了一种基于动态抽样的关联分析方法,这个方法的新颖之处在于设计了动态样本的关联规则相似度Sim(d1,d2),d1,d2是前后抽取的2个样本.当这2个样本的相似度值接近1时,2个样本上产生的关联规则不再有变化,进一步的抽样也不会再产生新的关联规则,此时就可以认为找到了可以代替总体进行关联规则挖掘的样本了.
文献[4]提出了一种针对关联分析的两步抽样法.第1步,随机抽取一个容量较大的初始样本,并计算出该样本中各个项的支持度;第2步,以前一步计算的支持度作为阈值去删除“孤立点”,留下具有代表性的项,构成一个能较好反映总体统计性质的容量较小的最终样本.在这个最终样本上的关联分析结果被证明能较好地反映总体上的关联规则.
文献[5]设计了一种被称为抽样错误估计(sampling error estimation(SEE))的动态抽样方法,认为:随着样本容量的不断增加,在样本上进行关联分析产生的错误将不断减少,如果将所有频繁项在样本上的支持度和它在总体上的支持度之差的均方根定义为错误度量值,那么,当这个均方根的值不再有显著变化时,就可以认为找到了代替总体进行关联分析的最优样本.
除上述的方法以外,文献[6]设计了Epsilon Approximation Sample Enabled(EASE)的抽样方法;文献[7]设计了EASIER方法,对EASE进行了改进;文献[8]利用马尔科夫链建立网络,并通过随机游走的方法抽取网络上的节点进入样本,解决了关联规则挖掘中项集提取的问题;文献[9-10]设计了一种基于序列插值的累进抽样法来提高关联挖掘的效率;文献[11]设计了一种基于新的累进抽样的方法,提高了关联挖掘的效率;文献[12]设计了从特征空间抽取随机样本序列的方法,以确定关联规则的方向性;文献[13]设计了micro-randomized方法,获得随机的关联项集,改进了Apriori方法的执行效率;文献[14]设计了Gibbs-sampling方法,减少了参加关联挖掘的项集个数,并在精简的特征空间中进行随后的关联挖掘.这些方法在寻找最优样本的过程中大多数都需要多次执行关联挖掘,可能会使抽样引起的开销大于其为挖掘带来的效率.
本文从数据挖掘中分类器性能比较的度量方法上得到启发,将这种度量方法引入到累进抽样的学习曲线构建中,在不执行关联挖掘的前提下,设计了一种新颖的累进抽样方法,利用关联规则的支持度找到一个能代替总体进行关联分析的最优样本.
1 理论与方法分析
在利用分类模型对不平衡数据进行分类挖掘时,通常需要对挖掘结果进行评价.对于二元分类,稀有类通常记为正类,而多数类记为负类.表1显示了汇总分类模型正确和不正确预测的实例数目的混淆矩阵.其中:真正数(f+,+(TP))(或简称TP)是指被分类模型正确预测的正样本数;假负数(f+,-(FN))(或简称FN)是指被分类模型错误预测为负类的正样本数;假正数(f-,+(FP))(或简称FP)是指被分类模型错误预测为正类的负样本数;真负数(f-,-(TN))(或简称TN)是指被正确预测的负样本数.
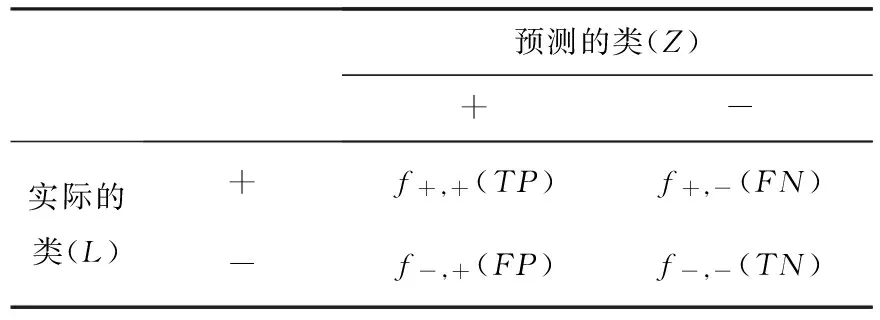
表1 二元分类问题的混淆矩阵
为了评价分类模型的分类效果,构造了准确率(P)、召回率(R)和F1度量3个指标,即
(1)
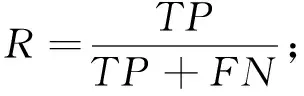
(2)

(3)
式(1)~式(3)中:P反映被分类模型预测为正类的样本中实际为正类的样本所占的比例;R反映所有的正类中能被分类模型正确预测的样本所占的比例.要使分类模型的性能良好,通常会平衡准确率和召回率的值,因为前者越大,犯假正类的错误就越小;后者越大,犯假负类的错误就越小.因此,将P和R合并成另一个度量,称为F1度量,该度量是准确率与召回率的调和平均数.
从式(1)和式(2)容易看出,P,R其实就是2个条件概率,可表示为
P=p(L=+/Z=+),R=p(Z=+/L=+).
进一步得,TP,FP,TN,FN服从参数为(λTP,λFP,λTN,λFN)的多项分布,即
P(D=(TP,FP,TN,FN))=
λTP+λFP+λTN+λFN=1.
其中:λTP,λFP,λTN,λFN分别表示分类挖掘结果中TP,FP,TN,FN实例数目占所有实例数目的比例.由多项分布的边缘分布和条件分布的性质,可写出P的似然函数为
L(p)=P(D|p)∝pTP(1-p)FP.
根据贝叶斯规则和先验分布假设可推出
其中,λ是形状参数.

1.1 基于抽样学习的关联规则算法设计
为了提高关联分析的效率,从总体中抽出一个样本,理想的,若抽到的样本中各个n-项集的频繁性与它们在总体中的频繁性相同,频繁度相似,则样本所产生的关联规则与总体产生的关联规则基本相同.但寻找和比较所有的项集是没有必要的,因为频繁项集具有向下覆盖性(若1-项集是非频繁的,则包含它的2-,3-,…项集都是非频繁的),所以只需要考察所有1-项集的频繁度即可.在总体D中设置一个最小支持度阈值minsup(D),同时为最终的样本设置一个最小支持度阈值minsup(S),总体D中的1-项集在随机抽样后以某个概率P进入样本S,相应的会产生4种情况:1)在D中频繁而在S中不频繁;2)在D中不频繁而在S中频繁;3)在D和S中都频繁;4)在D和S中都不频繁.根据表1所介绍的分类模型的混淆矩阵评估抽样的效果,抽样后对样本中的1-项集的频繁性产生了一个“预测”:第1种情况可表述为FN,第2种情况可表述为FP,第3种情况可表述为TP,第4种情况可表述为TN.由此可设计一个让抽样学习停止的规则,并由该规则计算出停止抽样的阈值.由此,产生了一个可代替总体进行关联挖掘的最优样本OS,该样本的容量即为最优样本容量OSS.本文设计的抽样停止规则表述为

(4)
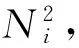
1.2 基于抽样学习的关联规则算法实现
本文所设计的基于累进抽样的关联分析算法简单,只需浏览数据总体一次,且不必重复执行关联规则挖掘,在动态的抽样学习过程中获得最优样本,且只在最终的样本上执行一次关联分析,无论在时间还是空间上都大大提高了挖掘的效率.以下给出该算法的描述:
输入:进行过简单预处理的数据总体
输出:最优样本OS
步骤1:遍历数据总体D以产生一个容量为ni=n0+200*i的随机样本序列{Si},i=1,2,3,…,同时计算所有1-项集的支持度(包括总体和各个样本中的1-项集).
步骤2:设置总体的最小支持度minsup(D),各个样本的最小支持度minsup(Si)=pi5minsup(D),其中,pi=ni/N,N表示总体的容量.
步骤3:从S1开始计算F(Si),当F(Sm)=F(Sm+1)=F(Sm+2)≈1时(为了避免随机情况的发生,对相同容量的样本进行若干次循环,以求得最大的F(Si)值,同时该等式可适当地延长至Sm+l,m+l 步骤4:用Sm+l代替D进行关联分析,得到具有较强概率保证的关联规则挖掘结果. 本算法在Windows 7系统下、8.00 G内存、i7-5600 U处理器的PC机上进行了效果测试,所用的数据来自2010年第6次全国人口普查浙江省人口普查长表,共有26 823个样本,17个属性变量,这些变量都是人口普查表中个人填报的项目,包括年龄、性别、职业、婚姻状况和受教育状况等相关内容.本文为了分析验证所设计的算法在关联挖掘中的优越性,以人口流动与就业分布的关联关系为挖掘目的,对该数据集进行了必要的预处理,最终有26 823个样本参加了关联分析. 对比Apriori算法、EASE算法和EASEIER算法,可明显看出该算法的优越性.图2是样本容量以200为步长,从200到12 600时各个样本与其对应的F(Si)值形成的学习曲线,其中,横坐标表示样本容量,纵坐标表示F(Si)值.与图1所显示的学习曲线的特性完全相同:当样本容量在[0,2 600]时,坡度陡峭,F(Si)值从0急速过度到0.902 1,这说明总体中接近90%的1-项集的频繁性被容量为2 600的这个样本准确地“预测”了,那么总体中与这些1-项集相关的关联规则都可以由这个样本来产生,换句话说,由这个样本产生的关联规则与总体产生的关联规则的一致率约为90%;当样本容量在[2 600,11 200]时,坡度相对平缓,F(Si)值从0.902 1缓慢地过度到0.973 1,说明当样本容量到达11 200时,总体中约97.31%的1-项集的频繁性被这个样本准确地“预测”了,若用这个样本代替总体进行关联挖掘,则准确率能达到97%左右;当样本容量在[11 200,12 600]时,学习曲线的坡度几乎为零,F(Si)值从0.973 1缓慢地趋于1,理论上说,总体的F(Si)值就等于1.如果以损失一部分的准确性为代价来提高挖掘效率,就可以选择OSS=12 600,或者选择更小的容量值. 样本容量图2 用F(Si)值刻画的样本学习曲线 本节将对抽样结果的有效性和可靠性进行评估:通过对抽样序列的F1度量值对比来完成有效性的评估;通过对总体、最优样本和拐点样本的关联挖掘结果对比来完成可靠性评估. 从表2可以看出:随着样本容量的增加,样本的F1度量值在逐渐增大,说明在此变化过程中,样本容量越大,样本对总体的频繁度信息保留就越多,特别是当样本容量达到由F(Si)值计算的最优样本容量时,F1度量值达到最大,此时的准确率P或者召回率R也将最大.因此,用样本的F(Si)值作为抽样停止的阈值这一抽样策略是有效的. 从表3可以看出:对学习曲线上的几个特殊点处的样本进行关联挖掘时,在相同的支持度和置信度评价前提下,随着样本容量的增加,样本产生的1-项集,2-项集,…,6-项集的个数越来越接近于对总体进行挖掘时产生的项集个数,特别是当样本的F(Si)值接近于1时,挖掘结果与总体几乎完全一致,说明在该样本容量下,抽样引起的频繁项集丢失问题可以被忽略,用该样本进行关联分析是可靠的. 表2 不同样本容量下样本的F1度量值对比 表3 学习曲线上特殊容量样本产生的频繁项集数对比 在相同的支持度阈值和置信度阈值下比较了学习曲线上各个特殊点样本产生的规则个数,结果如表4所示.从表4可以看出,容量为11 200和12 600的样本产生的规则个数与总体产生的规则个数非常接近.这一结果表明:根据F(Si)值产生的最优样本可以代替总体进行关联分析,它们之间因为抽样引起的关联分析的误差很小,用最优样本进行关联挖掘是可靠的. 表4 学习曲线上各样本在相同支持度与置信度下产生的规则数对比 根据关联挖掘的特点设计了一种新颖的累进抽样的方法,该方法将二元分类评估的混淆矩阵引入到因随机抽样引起的样本1-项集频繁性变动的问题中.因为频繁1-项集的个数是关联规则产生的基础,是所有后续关联挖掘的前提,所以本文设计的方法以此为切入点,针对抽样后1-项集频繁性变动的4种可能结果,以保证最终样本中的频繁1-项集个数与总体中的频繁1-项集的个数相同为抽样学习的目标,设计了累进抽样的停止公式. 本文设计的抽样停止公式以抽样的真正数、假正数、真负数、假负数为基础,以真正数和真负数最大化为获取阈值的临界点.根据抽样过程中F(Si)值相对于样本容量的变化关系来刻画累进抽样的学习曲线,然后根据学习曲线找到抽样停止的样本容量,并以该样本作为代替总体进行关联挖掘的最优样本. 为了验证本文设计的抽样学习公式是有效的、可靠的,用二元混淆矩阵的F1度量值进行评估.F1度量是抽样的准确率(P)与召回率(R)的调和平均值,当F1度量值接近于稳定值时,准确率或者召回率将达到最优,稳定值的选择取决于召回率或准确率.实践表明该抽样方法是有效的、可靠的. 在未来的研究中,还有以下几个方面的挑战:一是在刻画累进抽样的学习曲线时如何产生抽样序列,使得学习曲线的行为更良好;二是如何处理低支持度且高置信度规则的未入样问题. [1]Agarwal R,Srikant R.Fast algorithms for mining association rules[J].Journal of Computer Science and Technology,1994,15(6):619-624. [2]Provost F,Jensen D,Oates T.Efficient progressive sampling[C]//Proc of the 5th Conf on Knowledge Discovery and Data Mining.New York:ACM Press,1999:23-32. [3]Parthasarathy S,Zaki M J,Ogihara M,et al.Parallel data mining for association rules on shared memory system knowledge and information system[J].Knowl Inf Syst,2001,3(1):1-29. [4]Chen B,Haas P,Scheuermann P.A new two phase sampling based algorithm for discovering association rules[C]//The 8th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.Edmonton:ACM Press,2002:462-468. [5]Chuang K T,Chen M S,Yang W C.Progressive sampling for association rules based on sampling error estimation[J].Lecture Notes in Computer Science,2005,3518(1):505-515. [6]Dash M,Haas P,Haas P,et al.Efficient data reduction with EASE[C]//Proc of the 9th International Conference on KDD.Washington:ACM,2003:59-68. [7]Wang S,Dash M,Chia L T.Efficient sampling:Application to image data[C]//Advances in Knowledge Discovery and Data Mining of the 9th Pacific-Asia Conference.Hanoi:ACM,2005. [8]Fang M,Yin J,Zhu X.Supervised sampling for networked data[J].Signal Processing,2015,124(1):93-102. [9]Umarani V,Punithavalli M.Developing novel and effective approach for association rule mining using progressive sampling[C]//The 2nd International Conference on Computer and Electrical Engineering.Dubai:UAE,2009. [10]Umarani V,Punithavalli M.On developing an effectual progressive sampling based approach for association rule discovery[C]//International Conference on Information Management & Engineering.Chengdu:IEEE,2010. [11]Chakaravarthy V T,Pandit V,Sabharwal Y.Analysis of sampling techniques for association rule mining[C]//Database Theory:The 12th International Conference.Petersberg:ICDT,2009. [12]Lopez-Paz D,Muandet K,Schölkopf B,et al.Towards a learning theory of cause-effect inference[C]//The 32th International Conference on Machine Learning.Lille:JMLR,2015. [13]Rutterford C,Copas A,Eldridge S.Methods for sample size determination in cluster randomized trials[J].International Journal of Epidemiology,2015,44(3):1051-1067. [14]Qian G,Rao C R,Sun X,et al.Boosting association rule mining in large datasets via Gibbs sampling[J].Proceedings of the National Academy of Sciences,2016,13(18):4958-4963. [15]Goutte C,Gaussier E.A probabilistic interpretation of precision recall andF-score,with implication for evaluation[J].Chapman and Hall,1979,3408(2):345-359.2 实证分析

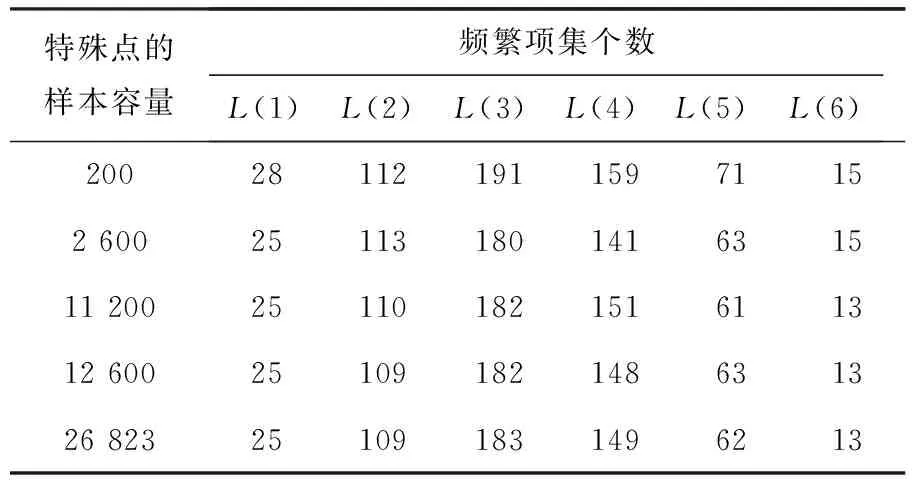
3 效果评估


4 结论与展望
