基于GRA与BP神经网络的沥青路面模量参数反演分析
2018-03-07刘锦俐陶珏强胡永举
邱 欣, 刘锦俐, 陶珏强, 杨 青, 胡永举
(浙江师范大学 工学院,浙江 金华 321004)
0 引 言
结构层模量参数是评价沥青路面性能状态的重要分析指标[1],而如何有效地利用落锤式弯沉仪(falling weight deflectometer,FWD)反演分析各结构层的模量参数,已成为道路工程领域的研究热点[2].当前,各国学者大多以静力连续层状体系为基础,开发各种结构层模量的反演分析方法,忽略了FWD测试过程的荷载动力效应,进而导致模量参数反演分析结果的准确度降低[3].事实上,沥青路面结构层模量反演问题存在变量多、耦合作用强、非线性等特点,而传统的数值回归分析、数据库搜索及迭代分析等方法,通常会产生求解精度低、稳定性差和非唯一等缺陷[4].因此,如何充分考虑FWD动力加载特性,并针对模型参数反演分析问题提出适宜的智能分析算法,已成为进一步推进FWD无损检测技术在铺面工程结构性能评价应用中的关键技术问题.为了充分反映FWD测点弯沉与结构层模量之间的高度非线性映射关系,国内外学者大都尝试利用神经网络分析方法对结构层的模型参数进行反演分析.美国陆军工程师Meier等[5]利用合成弯沉盆代替直接弯沉盆作为神经网络的输入,基于格林算法,利用BP(back-propagation,BP)神经网络对沥青路面的模量参数进行了系统反演分析;Sharma等[6]将FWD测点弯沉作为神经网络的输入,建立了沥青路面模量反演分析的BP神经网络模型,并可实现直接预测结构层的剩余寿命;Shafabakhsh等[7]在有限元模拟过程中考虑了荷载动力行为,构建了以面层厚度、基层厚度、移动荷载数量及速度为输入,结构层模量为输出的模量预测模型;查旭东等[8]在训练样本中加入噪音数据,比较了精确网络和噪音网络的反算能力;杨国良等[9]通过构建路表弯沉值与模量参数的对应数据库,在确定预测模型拓扑结构的基础上,采用BP神经网络对沥青路面的模量参数进行了反演分析.综上所述,国内外学者利用神经网络方法搭建沥青路面模量参数反演分析的拓扑结构时,通常以弯沉盆、厚度及荷载等参数作为输入变量,模量参数作为输出变量,研究主要集中在模型神经元个数及模型参数甄选等领域,未涉及各参数与模量之间的关联性分析,存在输入指标冗余、易造成学习过程噪音过多、模量参数反演精度下降等问题.
基于此,笔者充分考虑FWD测试荷载的动力效应,利用沥青路面动力有限元分析模型,构建FWD各测点弯沉与结构层模量参数的对应数据库,搭建以弯沉盆参数作为输入变量、各结构层模量作为输出变量的BP神经网络模量参数反演分析模型,并尝试利用灰色关联度分析方法(grey relational analysis,GRA)对BP神经网络的输入指标进行预处理,进而提升沥青路面模量参数反演分析的准确性与稳定度.研究成果以期为推进FWD测试技术在铺面工程结构性能评价分析中的应用提供新视角.
1 路面结构动力有限元分析模型
1.1 路面结构及材料参数
以典型半刚性基层沥青路面为例,将其简化为沥青面层(AC)、半刚性基层(BC)和路基(SG)等3层结构,通过改变各结构层模量参数取值,总计组装了124组典型路面结构.具体各结构层参数的取值范围见表1.

图1 分析模型网格划分

结构层厚度/m动态模量/MPa泊松比阻尼比AC0.182000~70000.350.05BC0.403000~140000.250.05SG∞100~4000.350.05
1.2 模型网格划分、尺寸及边界条件
采用平面4结点等参单元进行沥青路面几何模型的网格划分,径向方向上取5 cm作为网格长度单位,轴向方向上采用非均匀映射网格.为减小边界效应的影响,在不考虑下卧较浅刚性层影响的前提下,通过逐步试算确定模型径向长度为5 m、轴向路基深度为6 m作为最优模型尺寸.边界约束条件为左边界施加对称约束,右边界施加水平向约束,底部施加固定约束,结构层之间假定为完全连续[4].路面结构模型及网格划分见图1.其中,G1,G2,…,G9为9点传感器,其对应的弯沉值分别为d1,d2,…,d9.
1.3 荷载场确定
以PRI 2100型FWD测试设备为依据,采用半正弦函数表示FWD的测试荷载,荷载作用周期为0.03 s,荷载峰值为0.707 MPa,荷载作用半径为15 cm,函数表达式如式(1)所示.PRI 2100型FWD路表弯沉传感器布设情况见表2.
(1)
式(1)中:p(t)为测试荷载;pmax为荷载峰值;T为荷载周期;t为荷载作用时间.

表2 PRI 2100型FWD路表弯沉传感器布置方案
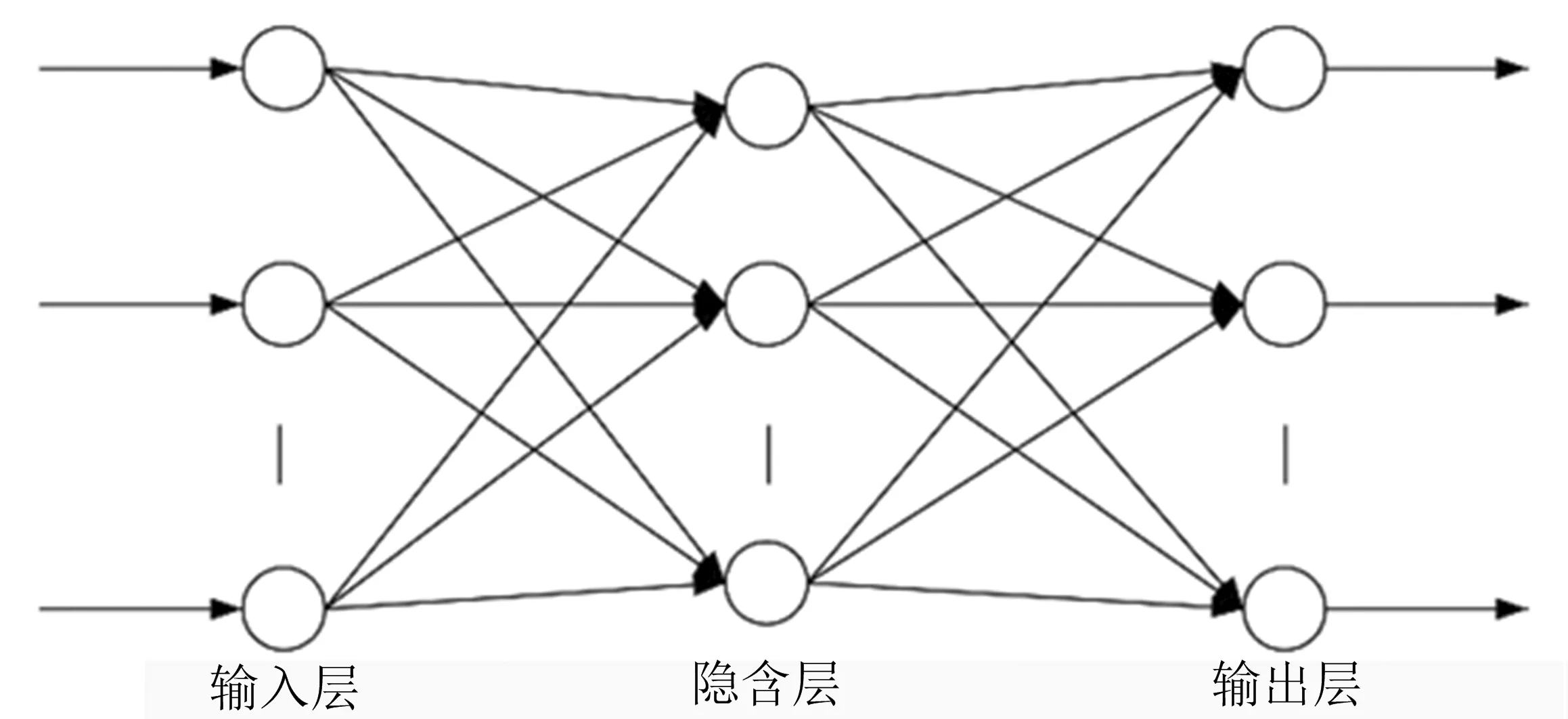
图2 三层BP神经网络模型结构
2 基于BP神经网络的模量参数反演分析
2.1 BP神经网络模型结构
BP神经网络,即误差反向传播网络.根据Kolmogorov定理,在隐含层神经元数目适合的情况下,BP神经网络可实现所有输入层与输出层间的非线性映射关系[10].分析中采用的三层模型拓扑结构如图2所示.
2.1.1 样本选取
BP神经网络模型构建过程中训练样本过少,不能包含所有状态,易导致模型预测精度的下降,而过多的样本则会导致训练过程的“麻痹”和“震荡”问题[11].因此,将124组弯沉与结构层模量参数对应数据库中的104组数据作为训练样本,用来构建模型;将剩余的20组数据作为测试样本,用来验证模型的有效性.
2.1.2 归一化处理
在构建BP神经网络模型前,需对训练数据进行变换处理,使训练数据在一定的阈值范围之内,以增加网络权值和阈值对各因子数值变化的灵敏度.本研究采用的样本归一化处理方法如式(2)所示.
(2)
式(2)中:x*为归一化后样本数据值;x为原始样本数据值;xmax为原始样本数据的最大值;xmin为原始样本数据的最小值.
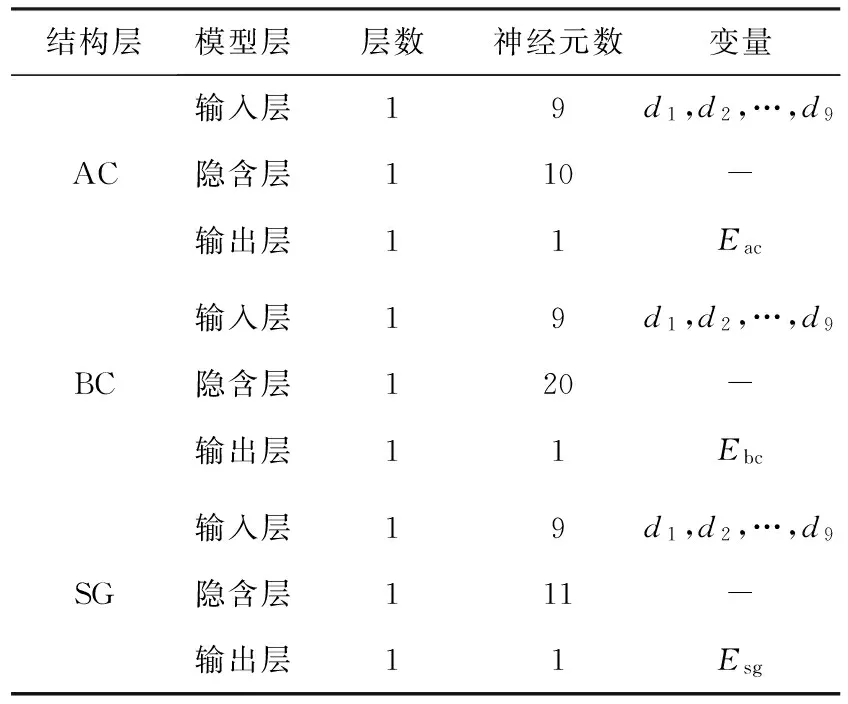
表3 BP神经网络拓朴结构设计方案
2.1.3 网络拓扑结构设计
对于BP神经网络分析模型而言,多输入单输出模型结构的精度明显高于多输入多输出的模型精度.因此,本文分别建立了3个对应于面层、基层和路基模量的多输入单输出的BP神经网络模型.其中,每个BP神经网络模型中的输入层神经元个数取9个,分别代表9点路表动态测试弯沉,输出层神经元数为1个,分别代表面层模量(Eac)、基层模量(Ebc)和路基模量(Esg).通过反复试算,隐含层神经元数目的取值范围为(10,20).具体BP神经网络的拓扑结构设计方案如表3所示.
2.1.4 网络模型控制参数设置
为形成合理的BP神经网络结构,需根据实际样本进行参数设置.由于TANSIG激活函数良好的非线性映射能力,能够将(-∞,+∞)的信号转换为(-1,1)的信号,且具有收敛速度较快、计算时间较短的特点,故选取连续可微的TANSIG双极性S函数作为输入层、隐含层和输出层的激活函数.为了提高沥青路面结构层模量反演分析的效率和准确度,训练函数采用基于LM优化规则的TRAINLM函数,进行网络权值和阈值的更新.为防止“过度拟合”引起过大的误差,设置误差达到0.001时为网络停止训练的条件.网络模型的控制参数如表4所示.

表4 BP神经网络的参数设置
2.2 网络模型有效性验证
将104组数据作归一化处理后,按照表4给出的神经网络控制参数对结构层模量(Eac,Ebc和Esg)的反演分析模型进行反复训练,在分别经过12,23和11步的训练达到预设收敛条件后,反演分析模型达到最优.训练完成后,将未参与训练的20组测试样本输入网络,以验证模型的精确度和稳定性.神经网络模型的模量输出值与目标值之间的误差分析结果如表5所示.

表5 模量输出值的误差分析表
由分析可知:1)不同结构层模量的均方根误差(RMSE)呈现差异,离散程度由小到大依次为:Esg,Ebc和Eac;2)最大相对误差(MD)出现于Eac的反演过程中,从大到小依次为Eac,Ebc和Esg;3)上述 BP神经网络模量反演模型的最大相对误差总体偏大,模量反演精度相对较低,有必要调整和改进BP神经网络模型,以提升模型的反演精度.
3 基于GRA的输入层弯沉参数调整分析
由FWD动力传播特征可知,路表弯沉是路面不同结构层力学响应行为的表达,不同测点弯沉的大小能够反映不同结构层的性能状态[3],故路表各测点弯沉与结构层模量的关联度不同.本研究尝试利用GRA方法,在确定路表弯沉与结构层模量关联度的基础上,实现对BP神经网络输入参数的寻优调整.
3.1 关联数列确定
3.2 无量纲化处理
无量纲化处理方法包括极值法、标准法及均值法等[12].为了得到反映各指标变异程度和相互影响的协方差矩阵,本研究采用均值法对数据数列进行无量纲化处理,如式3所示.本文以Eac子系统为例,其余2个子系统的处理方法与Eac相同.
(3)
3.3 关联度计算
以Eac子系统为例,对于一个参数列x0有n个比较数列x1,x2,…,xn的情况,采用式(4)表示各比较数列与参考数列在各个时刻的关联系数,其余2个子系统的处理方法与Eac相同.
(4)
式(4)中:γ(x0j,xij)是x0j与xij的关联系数;ζ是分辨系数,取0.5 ;Δmin=min{Δij,i=1,2,…,n;j=1,2,…,m};Δmax=max{Δij,i=1,2,…,n;j=1,2,…,m};Δij=|x0j-xij|.
将上述得到的测点弯沉与结构层模量的关联系数序列代入式(5),可得到两者之间的关联度,计算结果如表6所示.由此可见,各点弯沉值与结构层模量的关联度呈现不同的变化趋势.其中,d1,d4,d9分别与Eac,Ebc,Esg的关联度最大,体现了路表不同测点弯沉与路面不同结构层模量之间关联性的差异.
(5)

表6 弯沉参数与各结构层模量的关联度

3.4 调整权重分配系数
为最大程度减小反演过程的噪音干扰,区别输入层弯沉参数对于对应模量关联性的差异性,根据弯沉与结构层模量之间的关联度,采用式(6)调整BP神经网络输入层弯沉参数的权重分配系数,结果见表7.据此,在输出参数、网络拓扑结构和网络参数设置保持不变的情况下,重新进行BP神经网络的模量参数反演分析.
(6)

表7 弯沉输入指标的权重分配系数

4 基于GRA的BP神经网络模量参数反演分析
4.1 反演训练与精度分析
输入层路表弯沉参数调整后,BP神经网络模型对于结构层模量(Eac,Ebc和Esg)的反演分析训练曲线分别见图3~图5.由此可知,RMSE随着迭代次数的增加而递减,在分别经过47,42和50步的训练而达到预设收敛条件后,BP神经网络的模量预测值实现了与目标值最大程度的逼近,相关系数(R)分别为0.999 40,0.997 37和0.999 98.Eac,Ebc和Esg的反演预测值与目标值间的误差分析指标MD和RMSE分别为11.68%,1.20%;8.82%,2.51%及1.29%,0.33%.

(a)神经网络训练曲线 (b)精度分析曲线图3 面层模量反演分析训练与精度分析
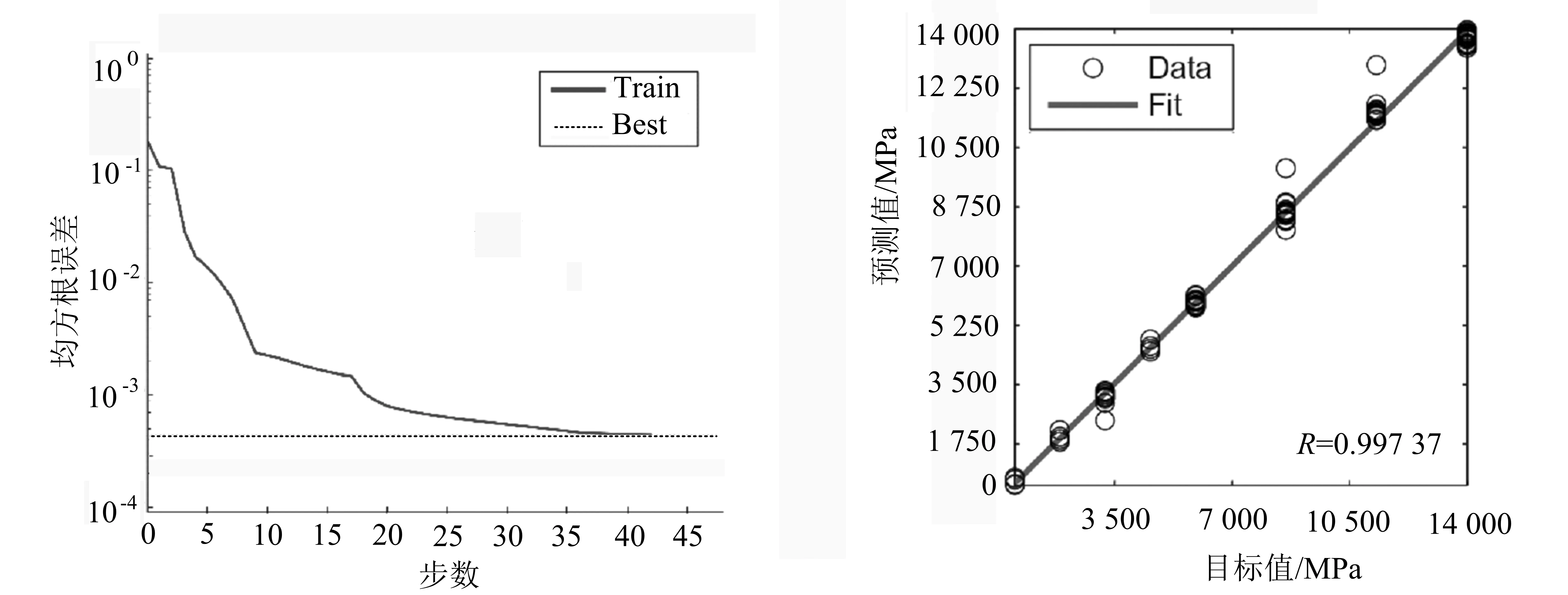
(a)神经网络训练曲线 (b) 精度分析曲线图4 基层模量反演分析训练与精度分析

(a)神经网络训练曲线 (b)精度分析曲线 图5 路基模量反演分析训练与精度分析
4.2 调整前后模量反演结果对比分析
输入层弯沉参数调整前后,BP神经网络模量反演分析的误差分析结果如图6所示.由此可知,Eac,Ebc和Esg反演分析结果的误差指标MD和RMSE均有所降低,其中MD分别降低了14.86%,2.73%和3.15%,RMSE分别降低了1.84%,0.02%和0.60%,模型精度和稳定性均有一定程度的提升;GRA改进后的BP神经网络模量反演模型对于提升Eac的准确性最为显著,其次依次为Esg和Ebc.

图6 改进前后BP神经网络模量参数反演结果的误差分析
5 结 论
基于沥青路面动力有限元分析模型,构建了路表弯沉与结构层模量的对应数据库,将灰色关联度与BP神经网络分析方法相结合,进行了沥青路面模量参数的反演分析,主要研究结论如下:
1)充分考虑FWD测试荷载的动力特征,构建沥青路面动力有限元分析模型是正确建立路表弯沉与结构层模量对应数据库的基础保障.
2)沥青路面结构层模量反演问题存在变量多、耦合作用强、非线性等特点,利用GRA方法,在确定路表弯沉与结构层模量关联度的基础上,进行BP神经网络模型输入层弯沉参数的调整分析,是提升结构层模量反演分析精确度的有效尝试.
3)相对于传统BP神经网络方法,GRA方法的引入提升了沥青路面各结构层模量反演结果的精度和稳定性,研究成果为进一步推进FWD测试技术在铺面工程结构性能评价分析中的应用提供了新的视角.
[1]谢辉,郭忠印,丛林.基于人工神经网络的沥青路面模量评估[J].同济大学学报:自然科学版,2007,35(8):1044-1047.
[2]Romanoschi S A,Metcalf J B.The errors in pavement layer moduli backcalculation due to improper modeling of layer interface condition[J].J Trans Res Board,2003,1639(2):36-42.
[3]邱欣,杨青,游庆龙.沥青路面阻尼特征参数及路表动态弯沉盆分布特征研究[J].公路交通科技,2013,30(7):1-6.
[4]邱欣,杨青,游庆龙.基于FWD动态弯沉盆参数的沥青路面模量反演分析[J].长安大学学报:自然科学版,2013,33(6):42-48.
[5]Meier R,Alexander D,Freeman R.Using artificial neural networks as a forward approach to backcalculation[J].Trans Res Rec J Trans Res Board,1997,1570(1):126-133.
[6]Sharma S S,Das A D.Backcalculation of pavement layer moduli from falling weight deflectom [J].Can J Civil Eng,2006,35(1):57-66.
[7]Shafabakhsh G A,Talebsafa M,Motamedi M,et al.Analytical evaluation of load movement on flexible pavement and selection of optimum neural network algorithm[J].KSCE J Civil Eng,2015,19(6):1-9.
[8]查旭东,王秉纲.基于人工神经网络的路面模量反算[J].交通运输工程学报,2002,2(2):12-15.
[9]杨国良,钟雯,黄晓韵.利用BP人工神经网络反算沥青路面基层弹性模量研究[J].路基工程,2016(4):78-81.
[10]张乃尧,栾天.基于模糊神经网络的模型参考自适应控制[J].自动化学报,1996,22(4):476-480.
[11]李萍,曾令可,税安泽,等.基于MATLAB的BP神经网络预测系统的设计[J].计算机应用与软件,2008,25(4):149-150.
[12]张文泉,赵凯,张贵彬,等.基于灰色关联度分析理论的底板破坏深度预测[J].煤炭学报,2015,40(s1):53-59.
