求解不可微算子方程的一类迭代法的半局部收敛分析
2018-03-07徐秀斌程春苗
徐秀斌, 程春苗
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
0 引 言
设X,Y是Banach空间,Ω⊆X是一开凸子集,H:Ω⊆X→Y为非线性算子,在Banach空间求解非线性算子方程
H(x)=0
(1)
的解是一个普遍的问题,在理论和工程技术方面都有广泛的应用.因此,有大量的文献研究该问题.最重要的方法之一就是牛顿迭代法[1-4]:若初始点为x0∈Ω,则
xn+1=xn-[H′(xn)]-1H(xn),n≥0.
(2)
显然,当H(x)不可导时,牛顿法就不可用了.在这种情况下,有一种有效的方法就是用差商去逼近牛顿法中的H′(xn).记L(X,Y)为有界线性算子空间.对x,y∈Ω,差商算子[x,y;H]∈L(X,Y)且满足
[x,y;H](x-y)=H(x)-H(y).
(3)
(4)
当H(x)不可微时,一些学者把H(x)分解成2个部分的和,即H(x)=F(x)+G(x).其中:F是可微算子;G是不可微连续算子.此时式(1)成为
F(x)+G(x)=0.
(5)
Zebrejko等[7]用修正的牛顿法
xn+1=xn-F′(xn)-1(F(xn)+G(xn)),n≥0
(6)
(7)
受文献[6,8]的启发,本文提出如下的一类新方法:
(8)
易知,当λ=2时,即得到方法(7).本文建立了迭代法(8)的半局部收敛定理,并通过数值例子说明该方法的有效性.
1 半局部收敛
这一节给出迭代法(8)的收敛分析.取初值x-1,x0∈Ω,并且假设:
(C1)‖x-1-x0‖≤α,y0=λx0+(1-λ)x-1∈Ω,λ≥1.
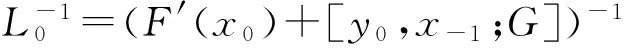
(C3)对∀x,y∈Ω,
‖F′(x)-F′(y)‖≤ω1(‖x-y‖).
(9)
式(9)中:ω1:R+→R+是连续不减的函数,ω1(0)≥0,存在一个连续不减的函数h:[0,1]→R+,使得ω1(tz)≤h(t)ω1(z),t∈[0,1],z∈[0,+∞).
(C4)对∀x,y,u,v∈Ω,有
‖[x,u;G]-[y,v;G]‖≤ω2(‖x-y‖,‖u-v‖).
(10)
式(10)中:ω2:R+×R+→R+是关于2个变量都连续不减的函数;ω2(0,0)≥0.
定理1假设条件(C1)~(C4)成立.记

再设方程
存在最小正根r.如果
β(ω1(r)+ω2((2λ-1)r+(λ-1)α,r+α))<1,
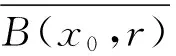
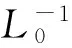
即x1∈B(x0,r).又因为
‖y1-x0‖=‖λx1+(1-λ)x0-x0‖=λ‖x1-x0‖≤λη 所以y1∈B(x0,r). 因为x1,y1∈B(x0,r),所以 β(ω1(r)+ω2((2λ-1)r+(λ-1)α,r+α))<1. (11) 即x2是有定义的. 又因为 G(x1)=G(x0)+[x1,x0;G](x1-x0), 所以 H(x1)=F(x1)+G(x1)= -(F′(x0)+[y0,x-1;G])(x1-x0)+F′(x0)(x1-x0)+ ([x1,x0;G](x1-x0)-[y0,x-1;G])(x1-x0)+ 从而 ‖H(x1)‖≤ ω2(‖x1-y0‖,‖x0-x-1‖)‖x1-x0‖+Tω1(η)‖x1-x0‖≤ (ω2((λ-1)α+η,α)+Tω1(η))‖x1-x0‖. (12) 由式(11)和式(12)可得 M‖x1-x0‖≤η. 同时, ‖y2-x0‖=‖λx2+(1-λ)x1-x0‖≤λ‖x2-x1‖+‖x1-x0‖≤(λM+1)‖x1-x0‖≤r, ‖x2-x0‖≤‖x2-x1‖+‖x1-x0‖≤(M+1)‖x1-x0‖≤r. 一般地,当xn-1,xn∈B(x0,r)时,类似上述分析可得: yn=λxn+(1-λ)xn-1∈B(x0,r); ‖xn+1-xn‖≤M‖xn-xn-1‖≤…≤Mn‖x1-x0‖≤η. 并且 ‖xn+1-x0‖≤‖xn+1-xn‖+‖xn-xn-1‖+…+‖x1-x0‖≤ 故{xn}是有定义的. 下证{xn}是柯西序列.∀p∈N,有 ‖xn+p-xn‖≤‖xn+p-xn+p-1‖+…+‖xn+1-xn‖≤ Mn(Mp-1+Mp-2+…+1)‖x1-x0‖= 因此,{xn}是柯西列,设它收敛到x*.再证x*是H(x)=0的解.因为 ‖H(xn)‖≤(Tω1(η)+ω2(λη,η))‖xn-xn-1‖, 所以,当n趋向正无穷时,‖xn-xn-1‖→0.由H(x)的连续性即知x*是H(x)=0的解. 最后证明唯一性.不妨设y*是H(x)=0的另一个解,y*∈B(x0,r).令 则 P(y*-x*)=H(y*)-H(x*)=0. 因此,如果P-1存在,那么必有y*=x*.实际上, β(ω1(r)+ω2((2λ-1)r+(λ-1)α,r+α))<1. 由Banach引理知,P-1存在,故y*=x*.定理1证毕. 考虑条件(C3)和(C4)的特殊情形: 假设方程 存在最小正根r.如果 考虑下列非线性方程组: (13) 式(13)中,(x1,x2)∈Ω:={(x1,x2)∈R2|x1,x2>0}.令 F=(f1,f2);G=(g1,g2). 易知 因此, β(ω1(r)+ω2((2λ-1)r+(λ-1)α,r+α))=0.316 81…<1,M=0.463 72…<1. 为了比较方法(7)和方法(8)的有效性,运用这2种方法计算了λ=1.1,1.2和2.0时的误差值‖x*-xn‖,计算结果如表1所示. 表1 误差结果 注:第1列为用方法(7)(λ=2)得到的结果;其余列为用方法(8)得到的结果. 从表1可以看出,方法(8)在λ=1.1和λ=1.2时的收敛速度比方法(7)更快一些. 对于取不同的λ值,半局部问题的收敛速度就会不一样.从理论上如何找到较优的λ还有待进一步的研究. [1]Ezquerro J A,Hernndez-Vern M A.Generalized differentiability conditions for Newton′s method[J].IMA J Numer Math,2002,22(2):187-205. [2]Ezquerro J A,Hernndez-Vern M A.On an application of Newton′s method to nonlinear operator withω-conditioned second derivative[J].BIT,2002,42(3):519-530. [3]Zehnder E J.A remark about Newton′s method[J].Commun Pure Appl Math,1974,27(3):361-366. [4]Li Chong,Wang Xinhua.Newton′s method on Reimannian manifolds:Smale′s point estimate theory under theγ-theory[J].IMA J Numer Anal,2006,26(2):228-251. [6]Kurchatov V A.On a method of linear interpolation for the solution of funcional equations[J].Dolk Akad Nauk SSSR,1971,198(3):524-526. [7]Zabrejko P P,Nguen D F.The majorant method in the theory of Newton-Kantorovich approximations and the Ptak error estimates[J].Numer Funct Anal Optim,1987,9(5):671-684.
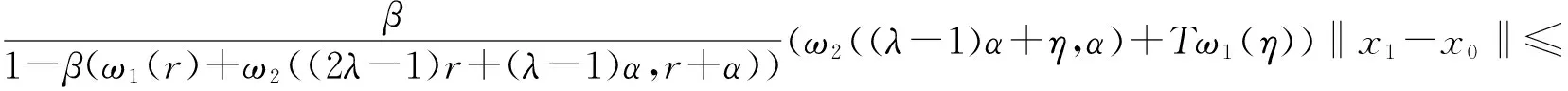
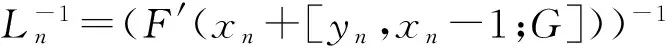

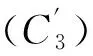
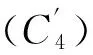
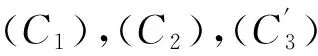

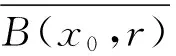
2 数值例子
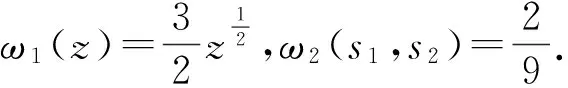

3 结 语
