探究一道中考题的解法

筅江苏省南京金陵中学河西分校 李玉荣

题目：（2018·武汉）如图1，在△ABC中，∠ABC=90°，P是边BC上一点，∠BAP=∠C，tan∠PAC=，求tan∠C的值.

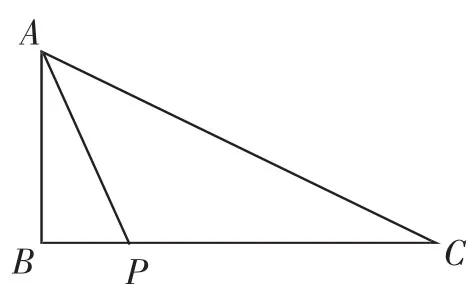
图1

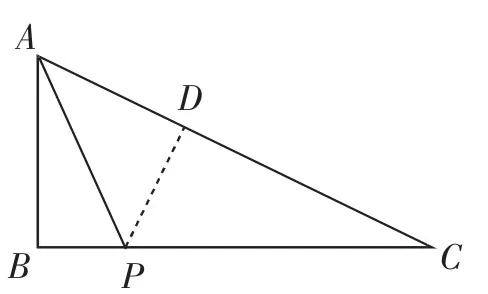
图2

尝试一：如图2，作PD⊥AC于点D.

解题陷入困境.

尝试二：如图3，作CD⊥AP交AP的延长线于点D……

与尝试一类似，陷入困境.

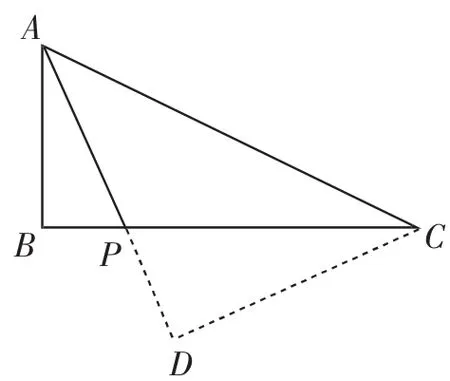
图3

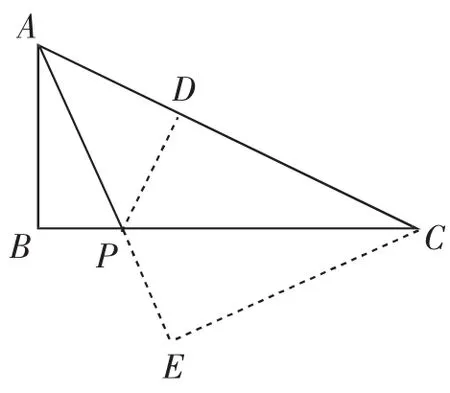
图4

尝试三：上述两次尝试是学生最容易想到的辅助线，遗憾的是未能求解，同时添加这两条辅助线如何呢？

解法1：如图4，作PD⊥AC于点D，作CE⊥AP交AP的延长线于点E.因为tan∠PAC=，所以可设PD=2k，AD=

根据勾股定理，得PA=3k.

易知∠PCE=∠BAP=∠PCD，所以PE=PD=2k.

所以AE=PA+PE=5k.

尝试四：将尝试一中的DP延长与AB的延长线相交如何？

解法2：如图5，作PD⊥AC于点D，延长DP、AB交于点E.

根据勾股定理，得PA=3k.

易知∠PEB=∠C=∠BAP，所以PE=PA=3k.

所以DE=PD+PE=5k.

尝试五：将尝试二中的CD延长与AB的延长线相交如何？

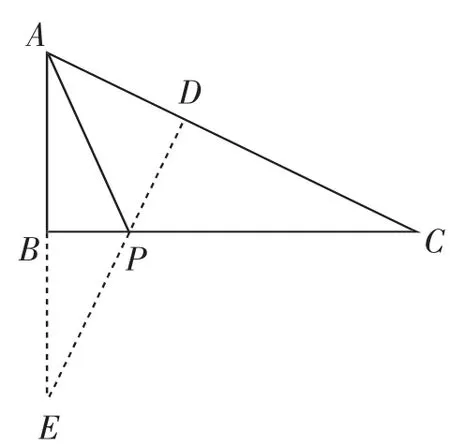
图5

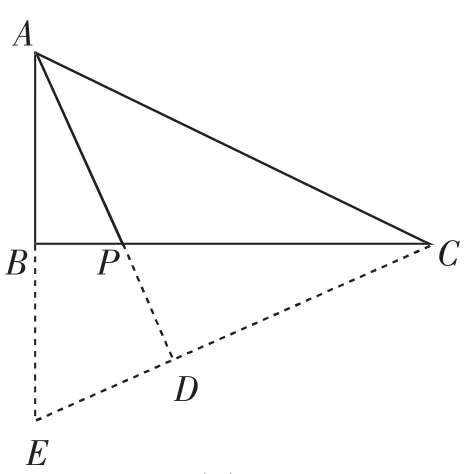
图6

解法3：如图6，作CD⊥AP交AP的延长线于点D，延长CD、AB交于点E.

根据勾股定理，得AC=3k.

易知∠BCE=∠BAP=∠ACB.又CB⊥AB，所以CE=AC=3k，所以DE=CE-CD=k.

尝试六：将尝试一中的DP⊥AC改为PD⊥AP如何？

解法4：如图7，过点P作PD⊥AP交AC于点D.

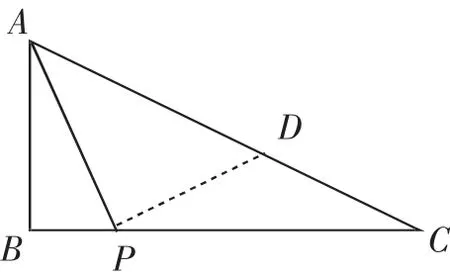
图7

根据勾股定理，得AD=3k.

易知∠DPC=90°-∠APB=∠BAP=∠C.

所以CD=PD=2k，所以AC=AD+CD=5k.

尝试七：将尝试二中的CD⊥AP改为CD⊥AC如何？

解法5：如图8，过点C作CD⊥AC交AP的延长线于点D.

根据勾股定理，得AD=3k.

易知∠DPC=∠APB=90°-∠PAB=90°-∠ACB=∠DCP.

所以PD=CD=2k，所以PA=AD-PD=k.

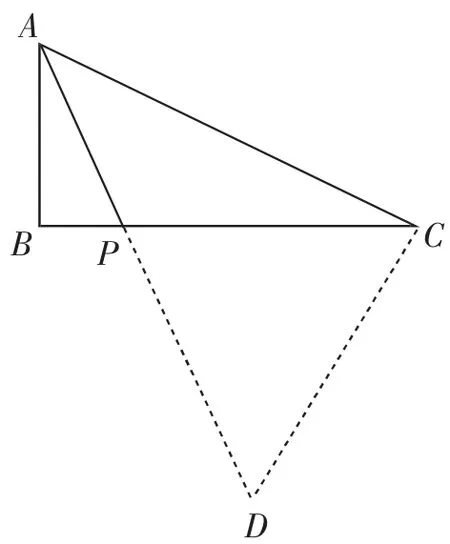
图8

尝试八：过点B作BD⊥AP于点D如何？

解法6：如图9，过点B作BD⊥AP于点D，交AC于点M.

易知∠MBC=∠BAP=∠C，所以BM=CM=AM.

根据勾股定理，得AM=3k，

所以BM=3k，BD=BM-DM=k.

尝试九：过点B作BD⊥AC于点D如何？

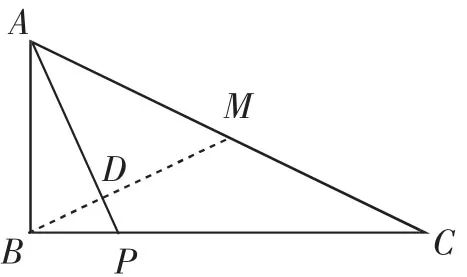
图9

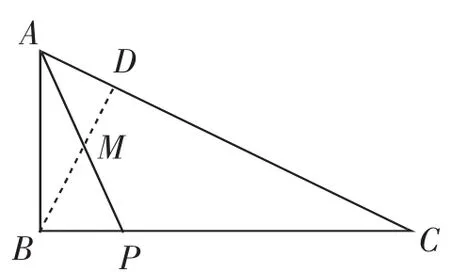
图10

解法7：如图10，过点B作BD⊥AC于点D，交AP于点M.

易知∠MBA=∠C=∠BAP，所以BM=AM=PM.

根据勾股定理，得AM=3k，BD=DM+BM=5k.

尝试十：在Rt△ABP中，以P为顶点，PB为一边构造一个角等于∠PAC如何？

解法8：如图11，以P为顶点，PB为一边作∠BPD=∠PAC，PD交AB于点D.

因为∠APB=∠BPD+∠APD=∠PAC+∠C，所以∠APD=∠C=∠BAP，所以PD=AD.

根据勾股定理，得PD=3k，AB=AD+BD=5k.

尝试十一：在Rt△ABC中，以A为顶点，AB为一边构造一个角等于∠PAC如何？

图11

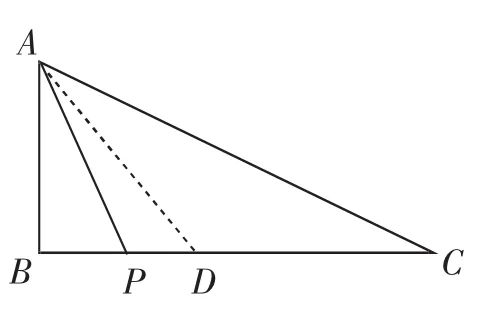
图12

解法9：如图12，以A为顶点，AB为一边作∠BAD=∠PAC，AD交BC于点D.

则∠DAC=∠BAP=∠C，所以CD=AD.

根据勾股定理，得AD=3k，BC=CD+BD=5k.

解题不可能是一帆风顺的，需要解题者在失败中重新尝试，在尝试中调整思路，逐步走向成功.挖掘中考试题的教学功能是一个重要的研讨主题，解题教学的着力点一定要落在学法指导（教会学生怎么想）和能力培养（如转化能力和迁移能力）上，“教什么”“怎样教”“教会什么”是值得每个数学教师研究的永恒话题.