精选课本题改编练习

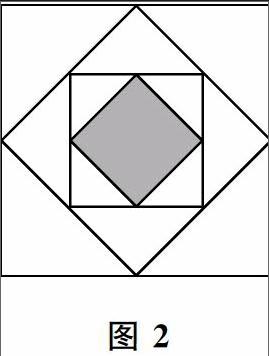
1.（课本原题）两个水平相当的选手在决赛中相遇，决赛采用五局三胜制，胜者获得全部的奖金，前三局打成2：1时比赛因故终止.有人提出按2：1分配奖金，你认为这样分配合理吗？为什么？

l-1.甲、乙两个选手在决赛中相遇，决赛采用五局三胜制，按以往的经验，每局比赛甲胜乙的概率为2/3，求比赛3局甲获胜的概率.

2.（课本原题）已知：数据x₁，x₂，…，x₁₀的均值为2，方差为3，求：数据2x₁+3，2x₂+3，…，2x₁₀+3的均值、方差.

2-1.已知：数据2x₁+3，2x₂+3，…，2x₁₀+3的均值为7，方差为12.求：数据x₁，x₂，…，x₁₀的均值、方差.

2-2.已知：数据x₁，x₂，…，x_n的均值为x，方差为σ²，

求：数据ax₁+b，ax₂+b，…，ax_n+b的均值、方差.

（命题人钱德平）

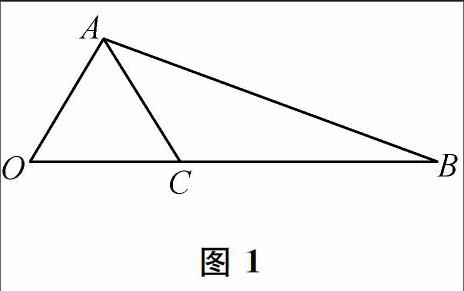
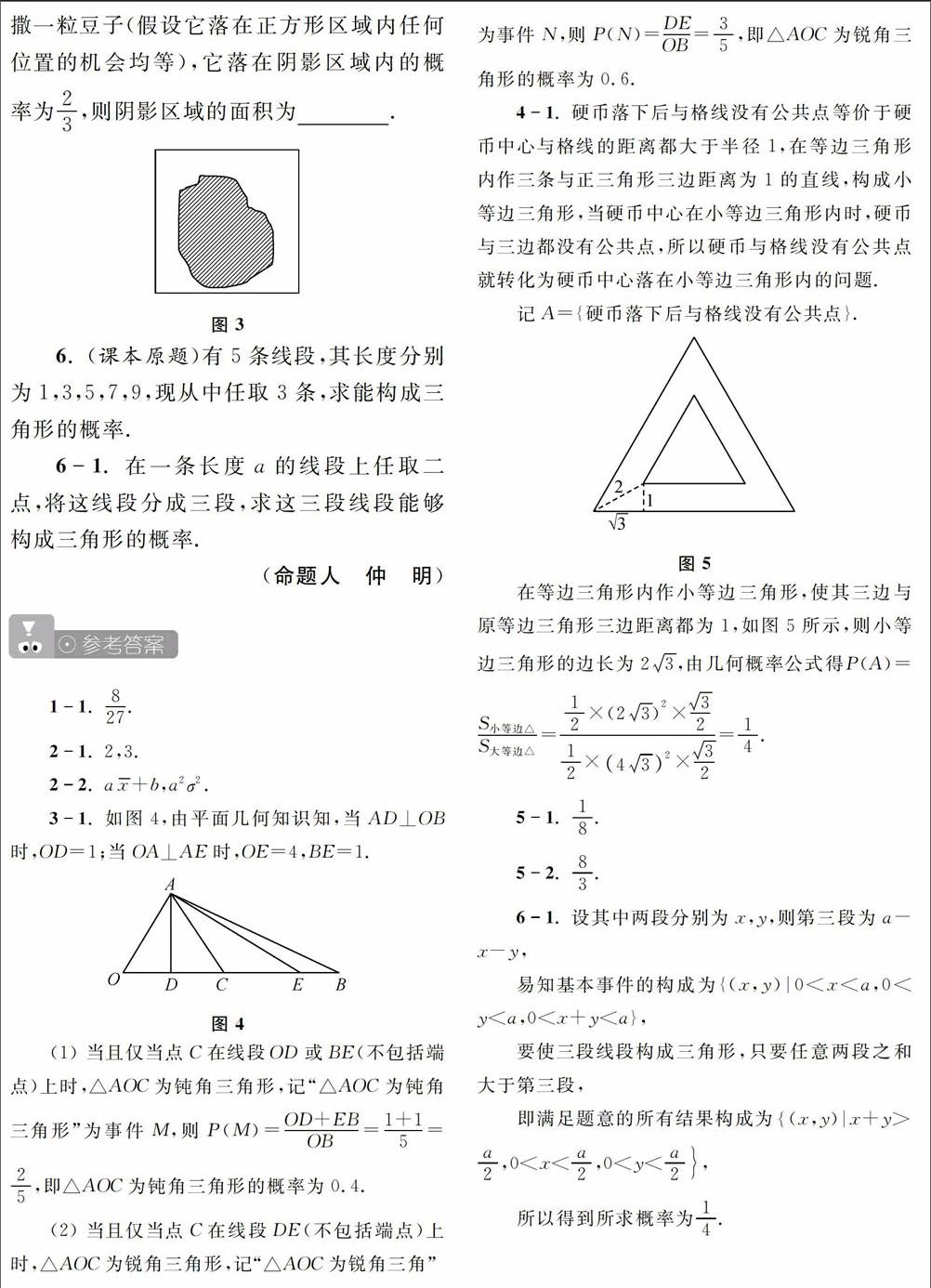
3.（课本原题）在等腰直角三角形ABC中，过直角顶点C在（x，y）/O

3-1.如图1，∠AOB=60。，OA=2，OB=5，在线段OB上任取一点C。

（1）求△AOC为钝角三角形的概率；

（2）求△AOC为锐角三角形的概率.（命题人 单建军）

4.（课本原题）设有一个正方形网格，其中每个最小正方形的边长都为6 cm，现用直径为2 cm的硬币投掷到此网格上，求硬币落下后与格线有公共点的概率.

5-2.如图3，边长为2的正方形中有一封闭曲线围成的阴影区域，在正方形中随机撒一粒豆子（假设它落在正方形区域内任何位置的机会均等），它落在阴影区域内的概率为2/3，则阴影区域的面积为

6.（课本原题）有5条线段，其长度分别为1，3，5，7，9，现从中任取3条，求能构成三角形的概率.

6 -1.在一条长度a的线段上任取二点，将这线段分成三段，求这三段线段能够构成三角形的概率.

（命题人 仲 明）

参考答件

1-1.8/27

2-1. 2，3.

2-2.ax+b，a²σ².

3-1.如图4，由平面几何知识知，当AD⊥OB时，OD=1；当OA_⊥AE时，0E=4，BE=1.

（1）当且仅当点C在线段OD或BE（不包括端点）上时，△AOC为钝角三角形，记“△AOC为钝角三角形”为事件M，则P（M）=（OD+EB）/OB=（1+1）/5=2/5，即△AOC为钝角三角形的概率为0.4.

（2）当且仅当点C在线段DE（不包括端点）上时，△A0C为锐角三角形，记“△AOC为锐角三角”为事件N，则P（N）=DE/OB=3/5，即△^0c为锐角三角形的概率为0.6.

4-1.硬币落下后与格线没有公共点等价于硬币中心与格线的距离都大于半径1，在等边三角形内作三条与正三角形三边距离为1的直线，构成小等边三角形，当硬币中心在小等边三角形内时，硬幣与三边都没有公共点，所以硬币与格线没有公共点就转化为硬币中心落在小等边三角形内的问题，

记A={硬币落下后与格线没有公共点}.

5-1，1/8.

5-2.8/3

6 -1.设其中两段分别为x，y，则第三段为a

易知基本事件的构成为{（x，y）/O

要使三段线段构成三角形，只要任意两段之和大于第三段，

即满足题意的所有结果构成为{（x，y）x+y>号，0

所以得到所求概率为1/4.