基于车轮安装惯性测量单元的车载组合导航

陈映秋，旷 俭，牛小骥，李 由，高柯夫，刘经南

（武汉大学 卫星导航定位技术研究中心，武汉 430079）

惯性导航系统（INS）具有实时性强、抗干扰、不受气象条件限制等优点。但由于惯性器件存在自身误差，会造成系统定位误差会随时间不断累积，导致其有长时间导航精度低的缺点。目前主流的做法是将误差不随时间积累的卫星导航定位系统（GNSS）作为定位精度控制手段，与INS进行组合导航定位，使用卡尔曼滤波对系统状态量进行最优估计，充分利用多系统相互之间的互补特性，既充分发挥惯导的自主推算能力又可以控制导航误差不随时间累积[1-2]。

现有的车载组合导航系统中，虽然主流的 INS/GNSS组合方式可以在很大程度上解决了误差累积的问题，但是GNSS受环境因素的影响较大，在复杂环境区域（比如城市峡谷），定位精度严重下降甚至在极端区域（比如隧道）不可用。因此，车载导航中多采用INS/里程计（ODO）组合导航作为补充，在GNSS定位受到环境影响时的短时间内仍然能够提供高精度的定位，构建一个更稳健、更高精度的车载组合导航系统[3]。

INS/ODO组合导航保留了 INS本身不需要任何外部信息的特性，同时大幅减缓了INS误差累积的速度，因此受到了广大研究工作者的关注并得到了较大程度的发展。这方面研究主要包括航位推算方法、基于航位推算过程误差模型的组合导航以及考虑部分里程计误差的惯导/里程计组合导航。然而，使用INS/ODO需要增加额外的里程观测传感器，增加了系统构建成本和系统算法复杂性，因此一定程度上限制了该方法的应用推广。

旋转调制技术是指当惯导的惯性传感器组合（ISA）做周期性的旋转时，垂直于旋转轴方向的陀螺和加速度计零偏引起的导航误差可以得到有效抑制，从而使惯性器件误差在短时间内的均值尽量接近零，以此来减小系统误差累计，提高导航精度[1-7]。但是，对转台的依赖也限制了旋转调制方案在低成本车载导航中的应用。

受旋转调制技术的启发，本文提出了一套基于低成本 MEMS-IMU的车轮安装导航方案。具体而言，将惯性测量单元（IMU）安装在车辆车轮中心，使IMU跟随车轮一起进行周期性旋转运动。相比传统 INS/ODO方案，本文方案利用了传统的INS机械编排算法，通过垂直于旋转轴的陀螺角速度输出结合车轮半径实时地获得精准的车体前向速度，取代对物理里程计传感器的依赖，从软件层面达到 INS/ODO组合导航定位的性能，从而节约成本，因此尤其适用低成本车载导航应用。此外，本方案还利用了车轮的周期性旋转特性，有效地降低陀螺零偏引起的位置误差。相对于传统安装方式的INS/ODO组合导航，具有成本更低、精度更高以及结构更简单的优势。

此外，本文方案还有如下创新点：

1）一方面发挥了传统惯性导航自主提供姿态、速度和位置的优势，另一方面利用IMU测量值结合轮式运动，挖掘出速度量测，提高自主导航性能。

2）综合多种运动信息构造卡尔曼滤波量测方程。推导了车轮安装IMU的两种测速模型，并利用前向速度，加上非完整性约束，构造三维卡尔曼滤波速度修正。此外，针对水平姿态角发散的情况，利用加速度计量测修正水平姿态角。

本文首先对车轮中心安装 IMU的机械结构以及算法流程进行了阐述说明，然后详细描述了组合导航卡尔曼滤波算法的设计和观测信息的使用，通过真实的轮式机器人载体测试对本方案的定位精度进行了较全面评测和比较，最后给出结论。

1 车轮安装IMU导航方案

本方案中利用 IMU最基本的角速度测量能力获得实时准确的里程速度，从而实现了无里程计传感器条件下的 INS/ODO组合导航。其基本设计思路为：将惯性测量单元安装在运动车辆的车轮中心并随车轮做同轴旋转运动，充分利用惯性导航能够真实反映载体运动轨迹的特性以及绝大多数情况下车轮只会向前或向后运动的特点，达到更低成本更高精度的目的。

图1给出了车轮安装IMU导航方案的详细数据处理流程：IMU输出的测量值用于惯导机械编排解算获得车轮的位置、速度和姿态；同时，垂直于车轮平面轴向（如图2中y轴）的陀螺输出值用于计算车轮的里程速度，平行于车轮平面两轴（如图2中x和z轴）的比力输出值用于计算水平角，然后使用扩展卡尔曼滤波进行数据融合，得到位置、速度和姿态的最优估计。另一方面，做周期旋转运动的 MEMS-IMU具有旋转调制效应，可以有效地抵消陀螺零偏对惯导系统误差的影响，提高数据质量[8]。下节将详细介绍上述方案中的组合导航卡尔曼滤波算法。

图1 数据处理流程Fig.1 Algorithm execution process

图2 坐标系示意图Fig.2 Axes definitions for wheel-fixed frame(b) and chassis-fixed frame(v)

2 组合导航数据融合算法

惯性导航是一种相对定位的导航方式，系统状态初始化是导航定位精度的基本条件，包括位置、速度、姿态[9]。在实际应用中，由于本方案中MEMS惯性传感器精度的限制不具备完全自主的对准能力，位置需要由 GNSS、全站仪或其他高精度手段给定。初始对准阶段一般为静态，初速一般设置为零，可由在静止条件下的加速度计输出计算横滚角、俯仰角，航向角通过GNSS的位置结果进行反正切计算确定。本方案可以作为INS/GNSS组合导航系统在GNSS受外界影响不可用情况下的一种补充方案。

2.1 卡尔曼滤波状态误差模型

本文中导航坐标系选取北-东-地的水平坐标系（n系），即原点为当前位置，x轴指向正北，y轴指向正东，z轴垂直x、y轴构成的平面垂直向下为正。其中惯性导航系统状态有三维位置误差 δrn、三维速度误差 δvn、三维姿态误差ψ、三轴陀螺零偏误差bg、三轴加表零偏误差ba，共15维，状态量如式(1)所示：

惯性导航系统的误差模型可由一个连续线性随机系统方程(2)表示[10]：

式中，X(t)为系统误差状态向量，F(t)是系统矩阵，G(t)是连续时间的系统噪声驱动矩阵，w(t)是系统噪声。对于低成本的MEMS惯性器件，精细的误差改正并不能带来明显的导航精度提升，因此离散化之后的惯导误差模型可简化为：

其中，

式中，I3和 03分别表示三阶单位矩阵和零矩阵，w是系统噪声向量，Φ为状态转移矩阵，Γ表示系统噪声系数矩阵，下标k是时刻标记，Cn表示由b系（即IMUb传感器坐标系，如图2所示）转换到n系的方向余弦矩阵，Δt表示IMU观测值相邻历元的时间间隔，τbg、τbf分别表示陀螺零偏和加速度计零偏建模为一阶高斯马尔科夫过程对应的相关时间，fn表示比力向量在n系下的投影。

在得到上述系统状态模型后，仍需要相应的观测模型利用修正信息改善系统状态的估计精度。线性化后的观测误差模型可用式(6)表示：

式中，δZk为观测向量误差，Hk是观测矩阵，vk为观测噪声。观测模型的具体设计将在2.2节中具体介绍。

2.2 卡尔曼滤波观测误差模型

本文的整体方案为惯性器件与里程计组合导航，特别之处在于惯性元件信息与里程信息均来源于同一器件，即安装在车轮中心的惯性导航模块。一方面，IMU的输出用于机械编排解算获得位置、速度、姿态；另一方面，IMU的测量中心与车轮轴心完全重合且进行同轴周期旋转（如图2所示），根据陀螺与车轮平面垂直轴的输出，结合车轮半径可得到前向速度信息。

此外，本方案进一步加入非完整性约束，与前向速度共同构成三维速度约束。非完整性约束是指载体在正常运动过程中，一般不会发生横向侧滑和垂向跳跃的现象，此时认为载体在横向和垂向的速度为零。

车辆在行进过程中通常符合此特性，因此除了沿车辆前进方向上的速度为vwheel，横向以及垂向速度为零[9]，即：

式中，里程速度由陀螺输出计算得到，ωy为陀螺y轴角速率输出，rw为车轮半径。

惯性导航推算的速度vn与车辆速度vv的关IMUwheel系如式(9)所示[9]：

式中，

式中，（Cn）表示矩阵Cn的第3行第1列对应的数值。b31b需要说明一点的是，本文只针对车辆在平坦道路的行驶环境进行测试，后续的讨论都将基于此假设展开。而对于更复杂的环境，需要对车辆进行横滚、俯仰角估计才能很好地计算安装角方向余弦矩阵，此处对该情况不做更多地描述。

另外，由里程计得到的速度观测模型如下：ev是速度的观测噪声。

综上，速度的误差观测方程可由式(13)表示：

2.3 卡尔曼滤波的更新

卡尔曼滤波分为预测和更新两个步骤，每次完成预测后，都需要对系统误差状态量进行更新：

式中，(δZk-HkδXk,k-1)为新息，代表新的量测信息与系统模型预测量的差异，增益矩阵K决定新息在更新过程中所占的比例权重。相应的误差协方差矩阵如下：

式中，P是状态量δX的协方差矩阵，Q是系统噪声方差阵。估计状态误差向量的协方差矩阵P可由式(16)(17)得到：

其中，R为观测向量的协方差矩阵。

本文中所采用的卡尔曼滤波为扩展卡尔曼滤波（EKF），EKF估计的误差是当前时刻系统状态量的估计值，即此种滤波器的工作形式是带有误差反馈的闭环修正。因此系统误差状态量在每次观测更新后，都将用于修正导航状态和参数，并将误差状态向量置零。

3 实验结果及数据分析

3.1 实验设备及环境

车载实验使用轮式机器人（PioneerP3-DX-SH）作为运动载体，IMU选用InvenSense公司的九轴运动传感器模块MPU9150，其主要性能参数见表1。

实验所用惯导模块为同一型号的IMU，具体安装情况如图3所示，固定在车轮中心为IMU1、固定在车身为 IMU2。在采集数据前，所有模块的零偏和比例因子都进行了实验室标定和补偿。

在试验场采集得到两个IMU的数据后，进行以下三种方案模式的数据处理和效果对比：

方案a：在IMU2数据做惯导解算的基础上，进行非完整性约束；

方案b：在IMU2数据做惯导解算的基础上，进行里程计速度和非完整性约束修正；

方案c：在IMU1数据做惯导解算的基础上，进行里程计速度和非完整性约束修正。

同时，利用INS/GNSS松组合解算并进行双向平滑后的结果作为参考真值。其中，GNSS接收机为天宝R9，数据处理方案为实时动态差分（RTK）后处理解算（精度可达厘米级），IMU数据为车身上的MPU9150提供，IMU和GNSS采样率分别为250 Hz和1 Hz。

表1 MPU9150性能参数Tab.1 Performance parameters of MPU9150

图3 模块安装环境及RTK实际参考轨迹Fig.3 IMU installation and the reference trajectory in Google Earth from GPS-RTK

本方案的理想工作情况是车辆置于完全水平的场地，而将实验小车置于图3所示的室外环境中，是因为可以利用GNSS定位结果作为绝对参考值来验证此方案的可行性，因此在后续分析中，仅考察该方案相比于传统方案在水平面（北向、东向）上的精度提升。实验过程中，控制小车围绕所在场地运动，动态实验持续约11 min，整个实验过程中实时采集IMU原始数据，对数据进行后处理解算和分析。

图3中右下角显示为小车运动的实际参考路径，在后续图中则会显示三种方案相对于 RTK参考结果的北向与东向位置误差图。表2则是三种方案的位置误差统计表。

图4中，由于行人对GNSS卫星信号的遮挡，解算所得的速度值会发生跳变，将GNSS速度粗差剔除后作为参考真值，考察使用轮上IMU陀螺角速度换算的速度的品质，其精度较为平稳，均方根误差约为0.075 m/s。

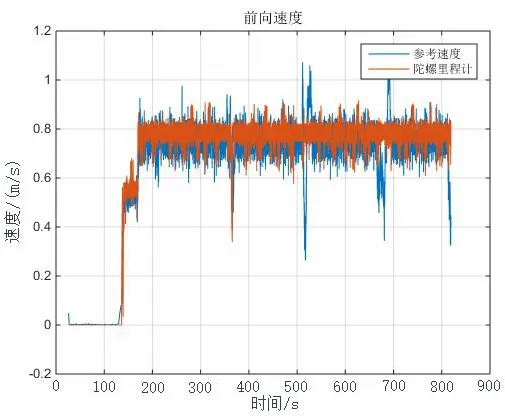
图4 由陀螺输出计算所得的前向速度Fig.4 Forward speed calculated from gyro output

由图5中各方案的轨迹可以看出：方案a只对车身上的IMU2模块进行数据处理，没有稳定的里程速度约束，位置误差发散较快；方案b采用车身IMU2与里程信息做组合，即传统车载组合导航方案，也得到了比较好的结果，但是需要额外的设备提供里程信息，成本相比单个IMU模块增加；本文方案处理结果在漂移与发散方面均有明显提升。

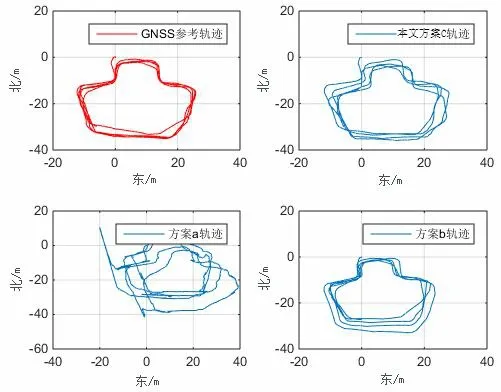
图5 各方案轨迹图Fig.5 Estimated trajectories of different methods

图6示出了三种方案相对于RTK参考结果的北向与东向位置误差图，由此可得：方案a由于没有融合里程计信息作为稳定的速度约束，误差发散较快；方案b相对于方案a来说，增加了里程计信息，北向位置误差的均方根误差（RMS）由6.50 m降低到3.64 m，东向位置误差的RMS由5.59 m变到3.15 m，垂向位置误差的均方根误差由1.70 m变到0.13 m；而本方案（方案c）相对于方案b，在北向上精度又提高了34.45%，东向上提高了 18.05%。因此，本车轮 IMU方案在北向和东向上的位置精度相较于其他两种方案均有明显提升。

图6 各方案误差图Fig.6 Estimated trajectories of different methods

表2 位置误差统计表Tab.2 Statistical table of position errors

实验结果表明，本文方案显著提高了安装在机器人车轮上的 MEMS-IMU的导航定位精度，实验小车在平均速度约为0.8 m/s的条件下运动11 min，平面位置RMS降低到3.52 m，相比于传统安装MEMS-IMU的导航方案降低了58.53%，相比于传统MEMS-IMU和里程计组合导航方案降低了29.67%。

高程方面，传统的 INS/ODO车载组合导航方案（方案b）精度最高，这是因为试验场地存在一定的坡度变化；而本方案的理想情况是在车辆在平整的水平面上行驶，因此在垂直方向的精度受到了一定影响。

4 结 论

本文采用了将MEMS-IMU模块安装在车辆车轮中心随车轮做周期旋转运动的方法。一方面，该方案类似于对MEMS惯导模块实时地进行旋转调制，能够有效地减弱了陀螺零偏对惯导定位误差的影响，在水平定位精度上取得了显著改善；另一方面，本方案由单个模块同时提供惯导原始数据和里程计信息（即车轮运动速度），在提高定位精度的前提下降低了设备成本和复杂度。

本方案仅使用一个低成本MEMS-IMU，通过软件算法取代了里程计传感器，从而提供对MEMS惯导误差的约束，达到并超越了“惯导+里程计”组合导航的效果，是一种适合于低成本车辆和轮式机器人导航定位的实用方案。

本文算法还存在一定的局限性，在平坦地面精度比较高，上下坡或者通用的路面算法局限性更加明显，因此在后续研究中会针对通用路面对算法进行改进。