利用h细化优化电阻层析成像灵敏度矩阵

肖理庆，王化祥，聂文艳



利用h细化优化电阻层析成像灵敏度矩阵

肖理庆1,2，王化祥3，聂文艳2

(1. 天津大学精密仪器与光电子工程学院，天津 300072；2. 淮南师范学院机械与电气工程学院，淮南 232038；3. 天津大学电气自动化与信息工程学院，天津 300072)

为了提高电阻层析成像图像重建质量，利用h细化优化灵敏度矩阵以改善其病态性. 以电阻层析成像有限元模型h细化区域的起始层数、终止层数以及三角形有限元内部区域所插入节点的横坐标、纵坐标为变量，以敏感场均匀分布时灵敏度矩阵条件数的倒数为适应度函数，利用h细化优化灵敏度矩阵，并将优化结果应用于改进Landweber预迭代算法图像重建. 实验结果表明，利用h细化可有效改善其病态程度，相比采取全局细化前后有限元模型对应的灵敏度矩阵，条件数分别降低了35.354,3%,、32.820,4%,，提高了重建图像分辨率.

电阻层析成像；h细化；灵敏度矩阵；病态性

电学层析成像技术包括电容层析成像[1-8]、电阻抗层析成像[9-13]、电阻层析成像[14-18]、电磁层析成 像[19-24]4种不同分支，具有非侵入、安全无辐射等优点．提高重建图像精度是加快电阻层析成像技术成功应用于实际系统的关键因素之一，而影响电阻层析成像技术重建图像分辨率的因素有很多，包括硬件系统与图像重建算法的性能、敏感场边界测量电压的有效数目(取决于敏感场阵列电极数目与数据采集模式)、敏感场边界测量电压的敏感性以及灵敏度分布的均匀性等．

目前常用的图像重建算法包括以线性反投影算法、截断奇异值分解、Calderon方法、D-bar方法为代表的非迭代类图像重建算法、以Landweber算法和Kalman滤波算法为代表的迭代类图像重建算法以及神经网络、智能算法、组合算法等其他不同图像重建算法[25-27]．在硬件系统性能、敏感场边界测量电压的有效数目等其他因素相同的实验条件下，基于灵敏度理论的图像重建算法逆问题求解精度主要取决于图像重建过程中所采用的灵敏度矩阵的病态程度．为了提高算法实时性，目前通常采取固定敏感场均匀分布时灵敏度矩阵不变的策略，因此，在其他实验条件相同的情况下，基于灵敏度理论的图像重建算法重建图像分辨率主要取决于敏感场均匀分布时灵敏度矩阵的病态程度．为了改善其病态性，提高图像重建算法求解逆问题的精度，目前通常采取正则化的方法．文献[17]通过采用全局细化有限元模型的方法，在不影响正问题计算精度的前提下，有效改善了Hessian矩阵的病态程度，但同时存在以下缺点：

(1)全局细化有限元模型并未降低敏感场均匀分布时灵敏度矩阵的条件数、改善其病态程度；

(2)全局细化有限元模型对应的结果并非最优值，且三角形有限元的形心并非所插入节点的最优位置．

为了克服上述不足之处，本文在可有效提高正问题计算精度的有限元模型基础上，以优化敏感场均匀分布时灵敏度矩阵为目标，以有限元模型h细化区域的起始层数、终止层数以及三角形有限元内部所插入节点的横坐标、纵坐标为变量，同时针对电阻层析成像技术中正问题与灵敏度矩阵计算繁琐的特点，利用计算量较小的改进粒子群算法[28]，h细化电阻层析成像有限元模型，有效降低了灵敏度矩阵的条件数．

1 基于改进粒子群算法的有限元模型h细化

本文所采用的h细化方法是在细化有限元模型的过程中，保证原有三角形有限元的边界不发生变化．为了避免在细化过程中出现需施加局部约束的悬空节点，本文采用在有限元模型确定采取细化区域的三角形有限元内部区域插入一个节点的方法实现h细化，其中采取h细化的区域(有限元模型的起始层数与终止层数)以及三角形有限元内部区域所插入节点的位置由改进粒子群算法确定．

步骤1建立提高正问题计算精度的有限元模型.

步骤2在确定适应度函数的基础上，以步骤1所得的可有效提高正问题计算精度的有限元模型h细化区域的起始层数、终止层数以及三角形有限元内部区域所插入节点的横坐标、纵坐标为变量，利用改进粒子群算法h细化步骤1所得的可有效提高正问题精度的有限元模型．根据在有限元模型不同h细化区域，分别插入三角形有限元形心与内切圆圆心对应的适应度函数的最大值，生成改进粒子群算法初始种群，并更新粒子速度与位置．

适应度函数为

   (1)

粒子速度和位置更新公式为

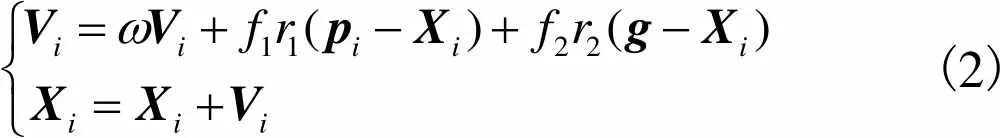
   (2)

   (3)

   (4)

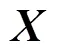
   (5)

2 仿真实验与分析

2.1 参数设置

2.2 不同有限元模型参数比较

根据步骤1所得可有效提高正问题计算精度的有限元模型如图1(a)所示；利用改进粒子群算法在文献[17]的基础上，对全局细化有限元模型时插入节点的位置进行优化所对应的有限元模型如图1(b)所示；本文提出的利用h细化优化灵敏度矩阵对应的有限元模型如图1(c)所示，优化曲线对应的模型如图2所示；计算边界电压测量值时采用图1(d)所示的 模型．

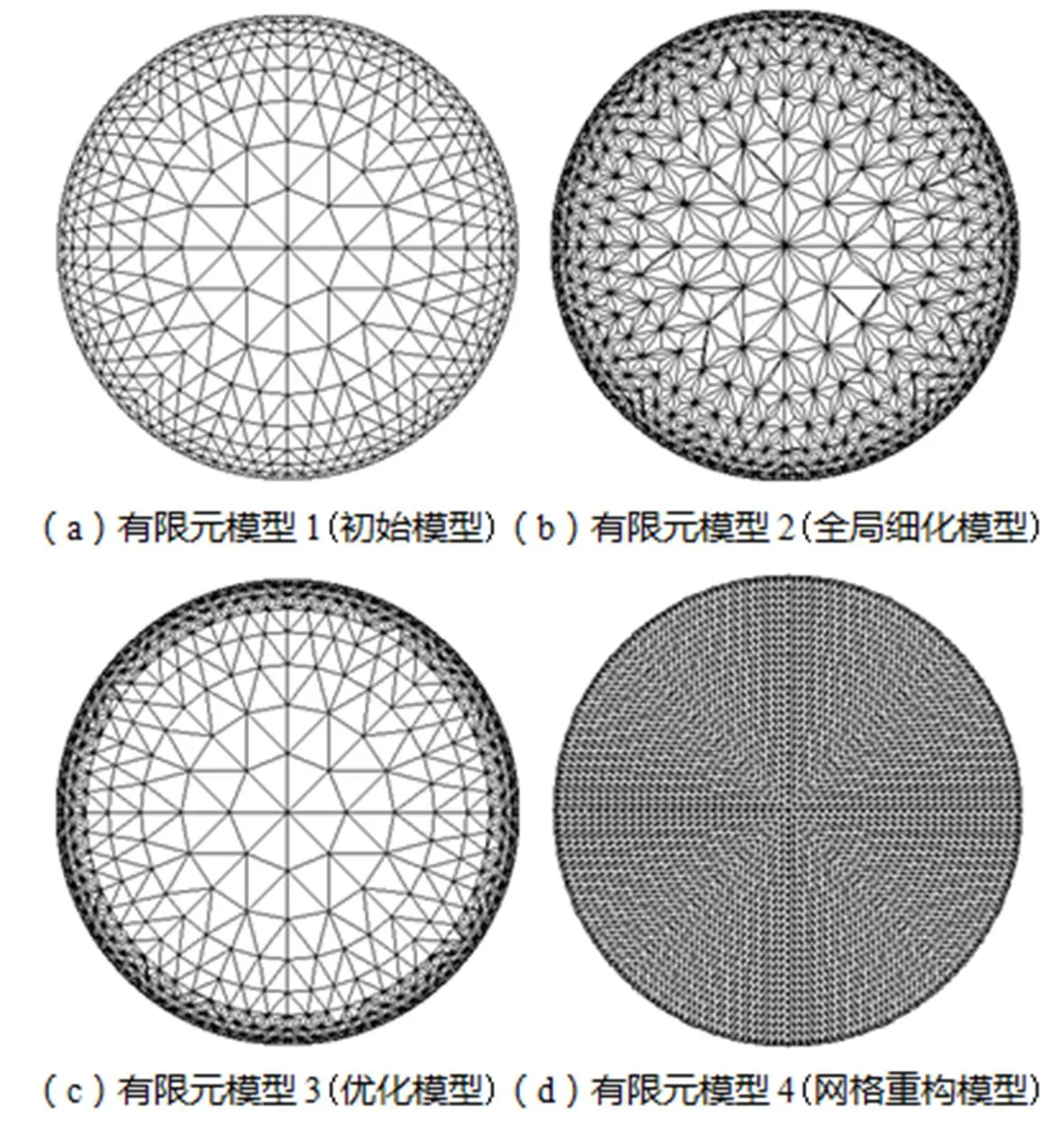
图1 不同有限元模型示意

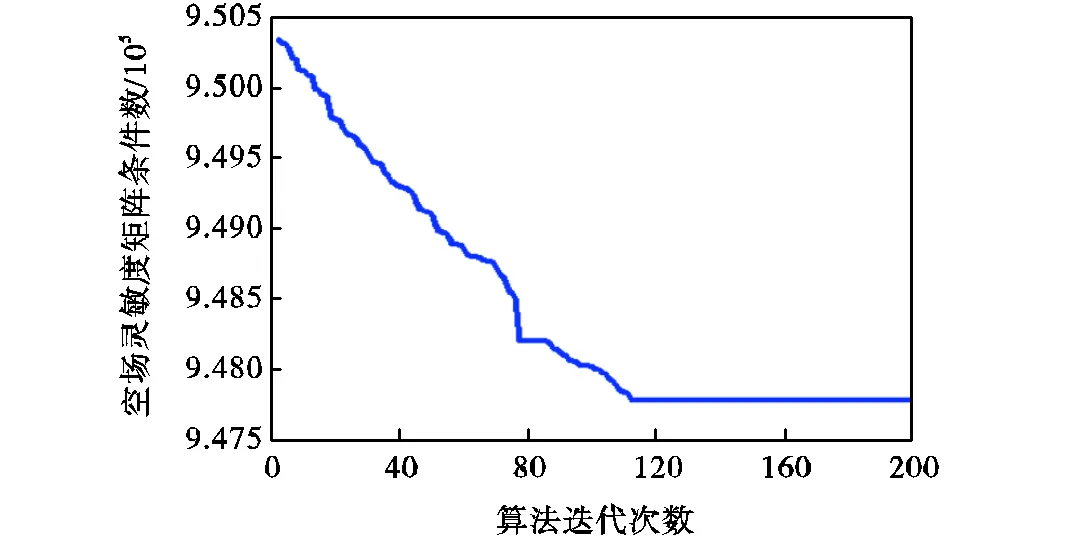
图2 算法收敛曲线

根据图2改进粒子群算法收敛曲线，结合图1改进粒子群算法最优结果对应的有限元模型3可知，如上所述，敏感场均匀分布时灵敏度矩阵的条件数不仅与有限元模型采取h细化的区域有关，而且与h细化时所插入节点的位置有关．

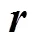
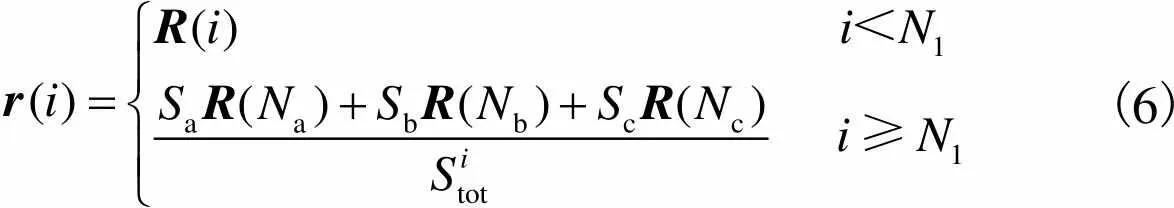
(6)

在相同实验条件下，有限元模型1～3所对应的敏感场均匀分布时的灵敏度矩阵的条件数分别为1.466,1×106、1.410,8×106、9.477,7×105．由有限元模型1、2所对应的敏感场均匀分布时灵敏度矩阵的条件数可知，全局细化有限元模型时，三角形有限元形心并非所插入节点的最优位置，利用改进粒子群算法优化全局细化时所插入节点的位置，可将敏感场均匀分布时灵敏度矩阵条件数降低3.771,9%,．而本文提出的利用h细化优化灵敏度矩阵，是通过改进粒子群算法确定采取h细化的区域以及三角形有限元内部区域所插入节点的坐标，与有限元模型1、2相比，有效改善了灵敏度矩阵的病态程度．

2.3 图像重建结果比较

为了验证本文提出的利用h细化优化灵敏度矩阵在提高图像重建质量方面的有效性，设置如图4所示6种仿真模型，图像重建算法选取基于改进粒子群算法离线优化灵敏度矩阵与离线选取算法增益因子的改进Landweber预迭代算法[29]，图像重建结果如图5～图7、表1和表2所示．

图4 仿真设置模型

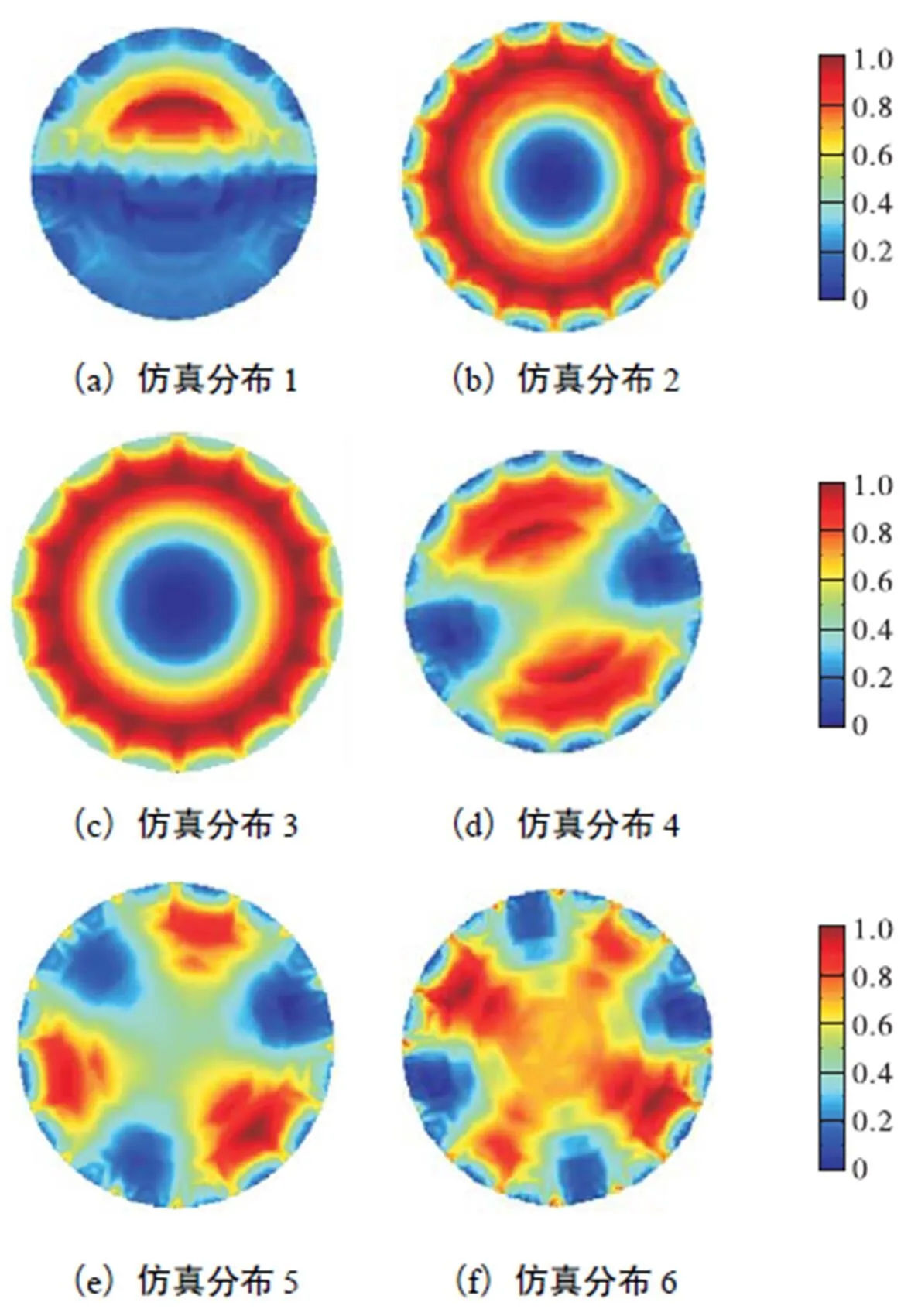
图5 有限元模型1重建图像

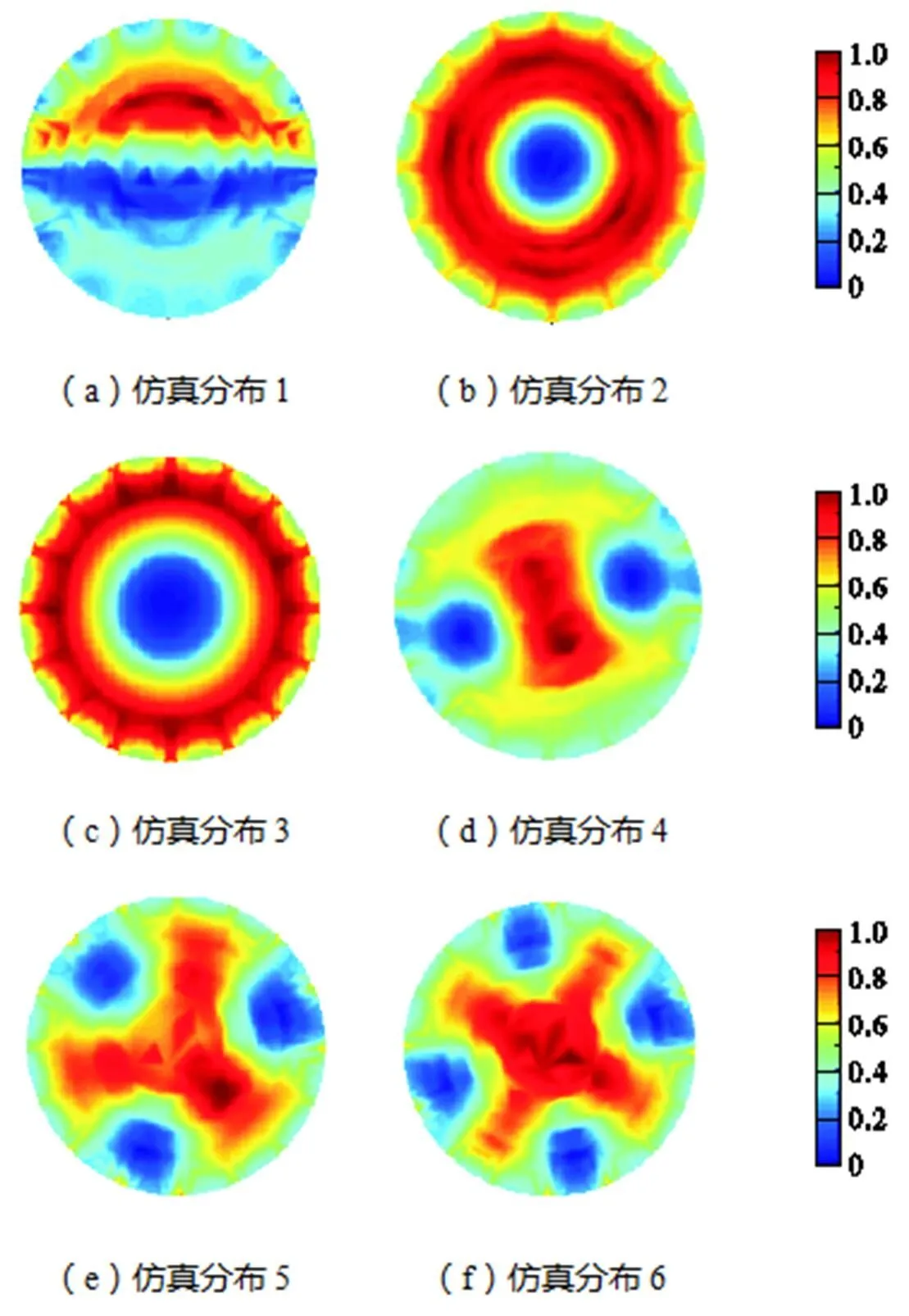
图6 有限元模型2重建图像

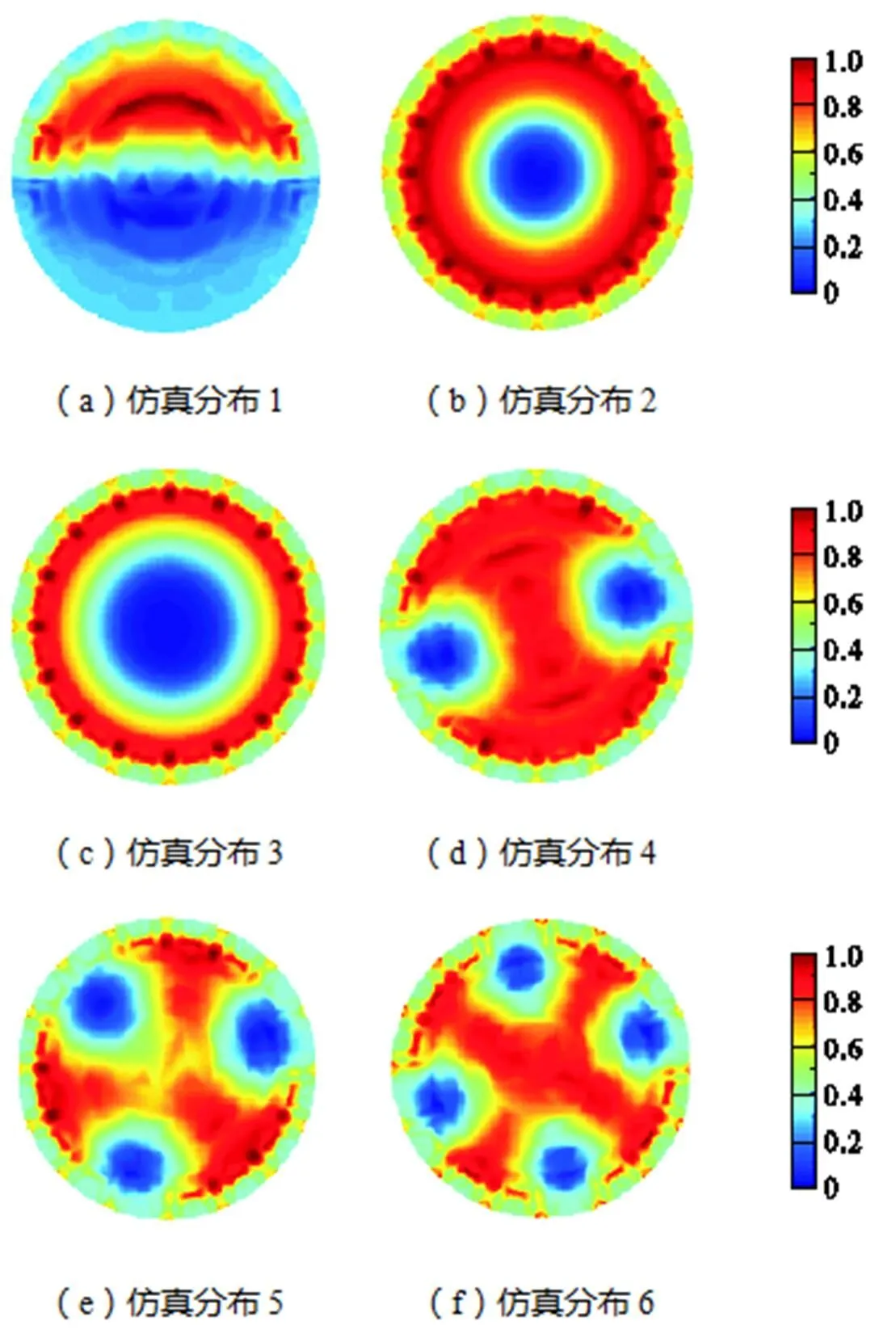
图7 有限元模型3重建图像

表1 不同模型相关系数比较

Tab.1 Comparison of correlation coefficients between different models

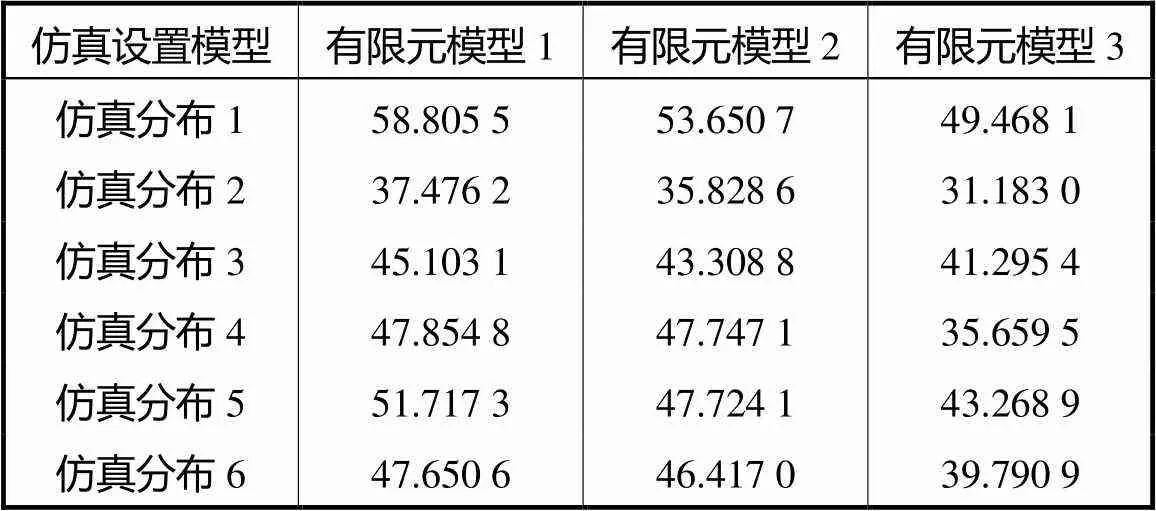
表2 不同模型图像相对误差比较

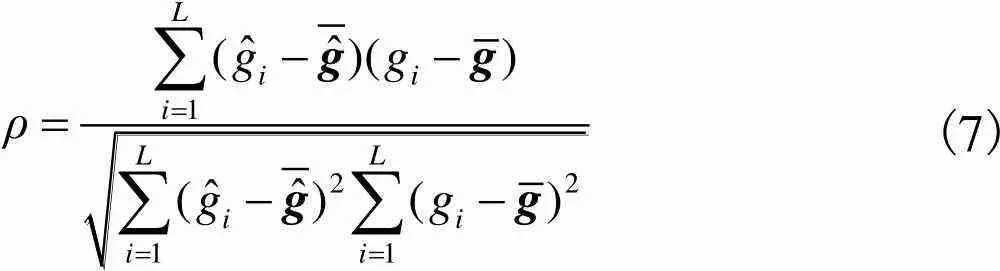
   (7)

   (8)

在相同实验条件下，3种不同有限元模型求解逆问题所消耗的时间分别为0.15～0.16,ms、0.46～0.47,ms、0.31～0.32,ms．与有限元模型1、2相比，本文提出的利用h细化优化灵敏度矩阵对应的有限元模型3基本不影响算法实时性．

由表1和表2可知，在相同实验条件下，3种不同有限元模型相关系数的平均值分别为0.643,3、0.669,0、0.746,0，图像相对误差的平均值分别为48.101,2%,、45.779,4%,、40.111,0%,．与有限元模型1、2相比，本文提出的利用h细化优化灵敏度矩阵对应的有限元模型3有效提高了图像重建精度．

为了验证噪声干扰下，本文提出的利用h细化优化灵敏度矩阵在提高电阻层析成像图像重建质量方面的有效性，将边界电压测量值加入5%,幅度随机噪声，图像重建结果如图8～图10、表3和表4所示．

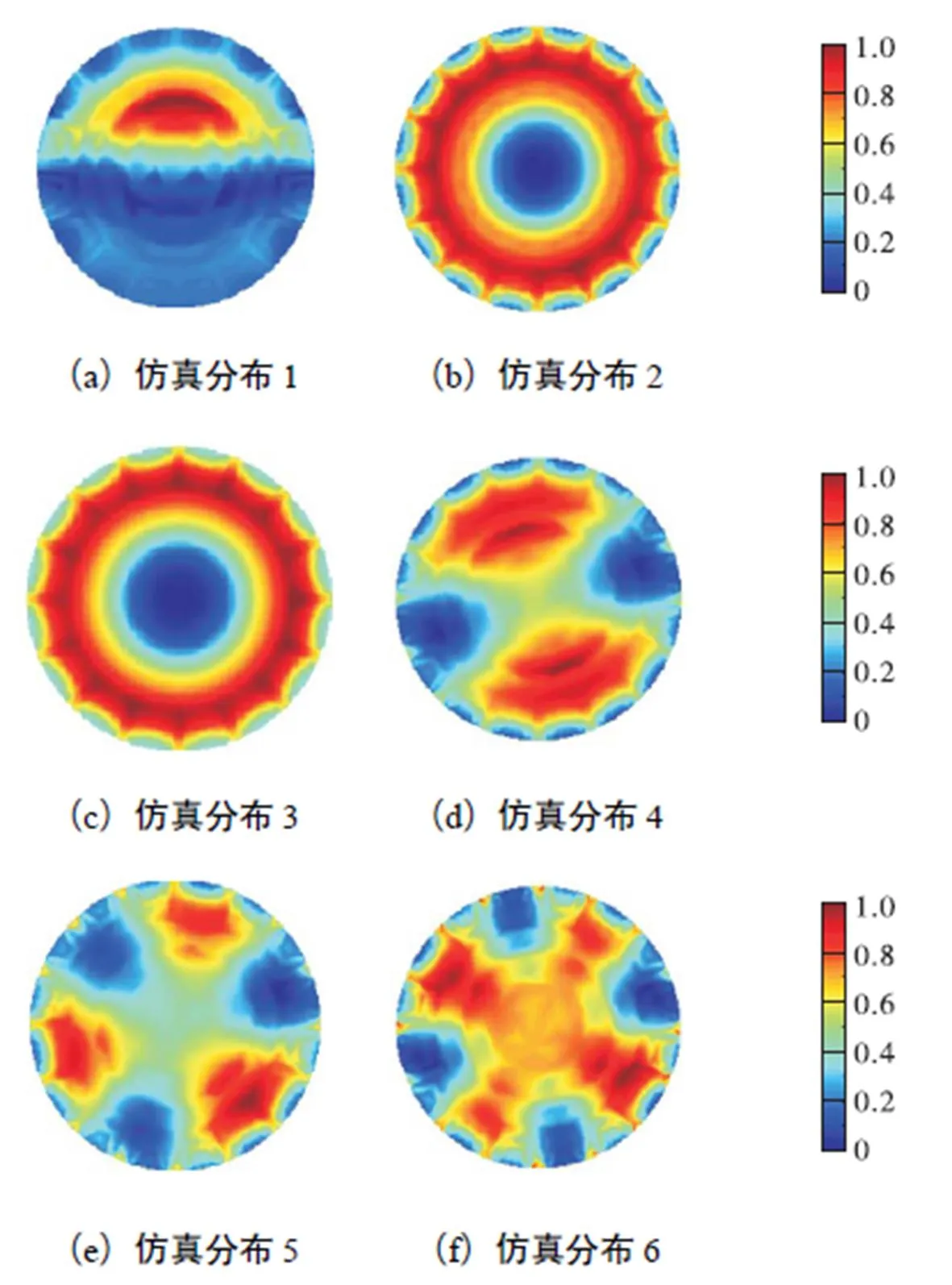
图8 噪声干扰下有限元模型1重建图像

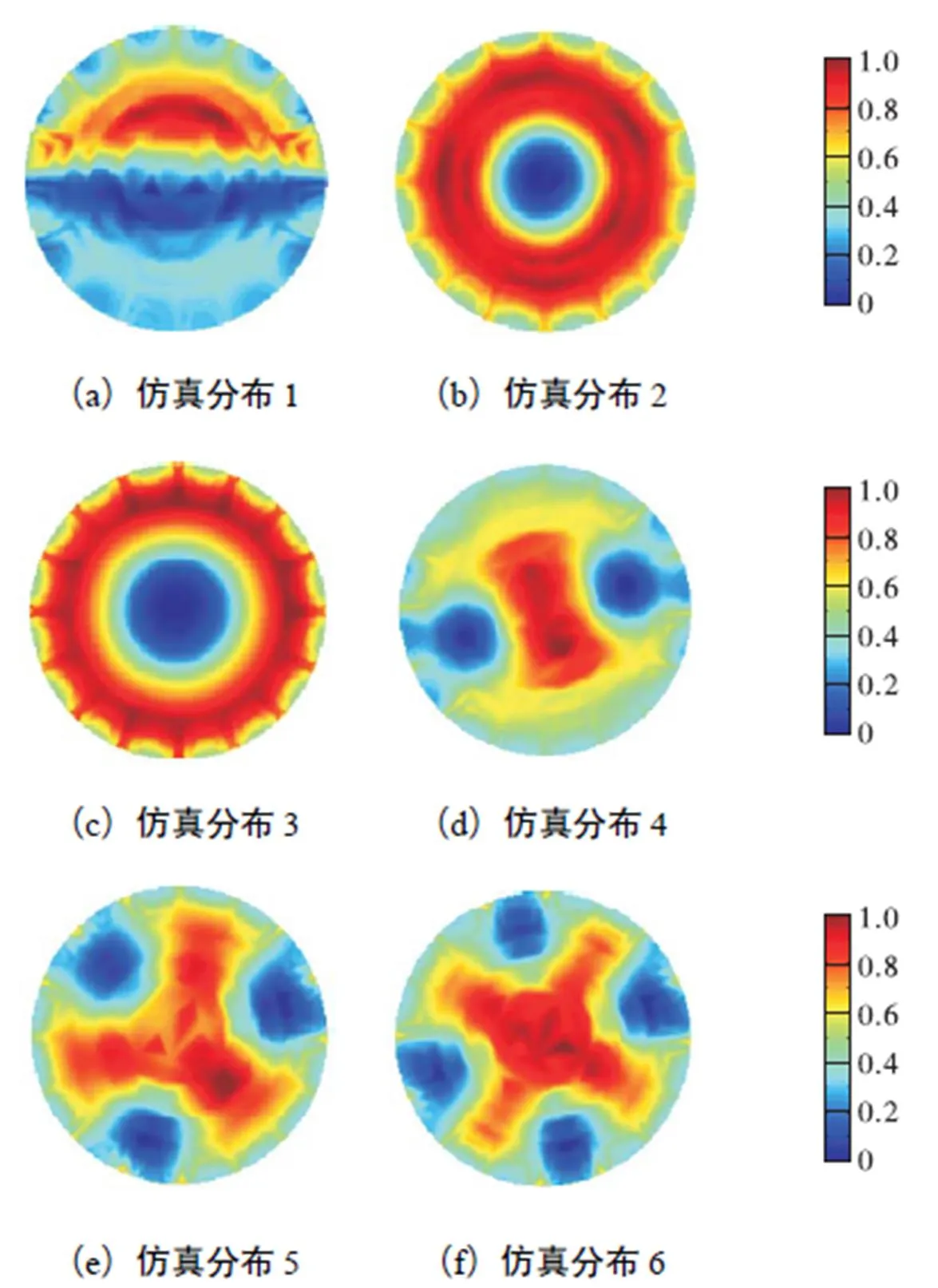
图9 噪声干扰下有限元模型2重建图像

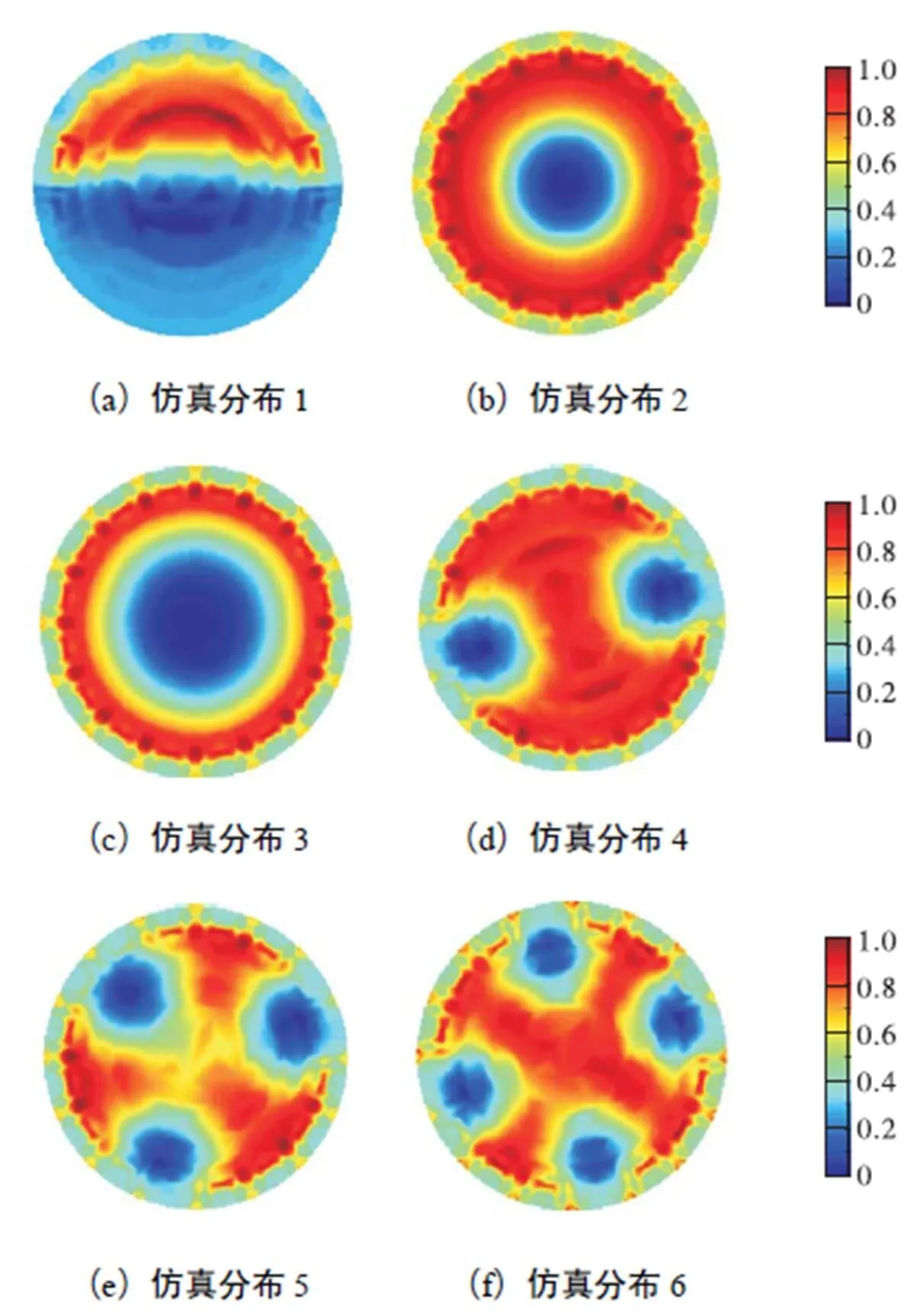
图10 噪声干扰下有限元模型3重建图像

表3 噪声干扰下不同模型相关系数比较

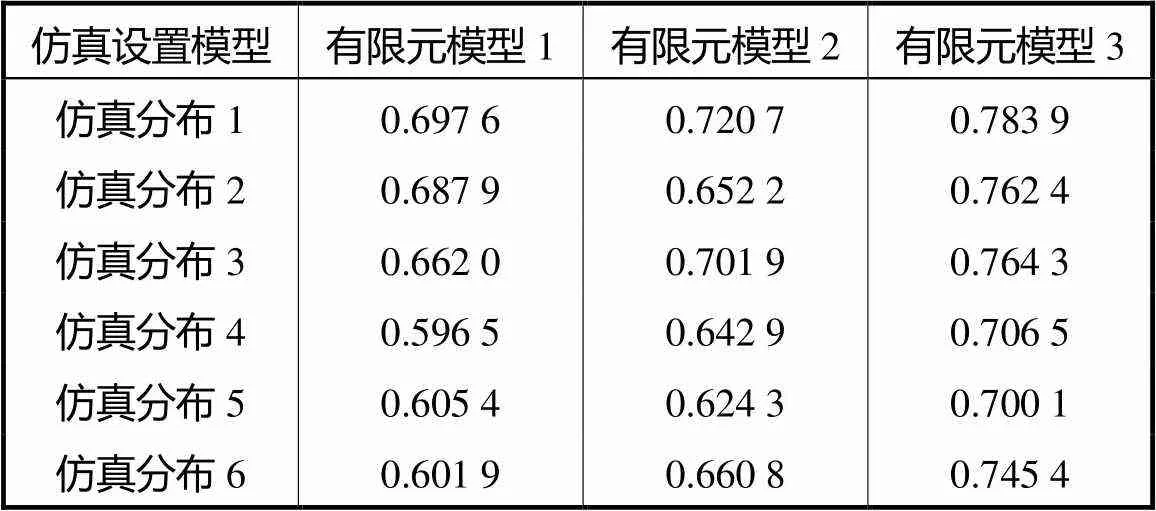
Tab.3 Comparison of correlation coefficients between different models with noise disturbance

表4 噪声干扰下不同模型图像相对误差比较

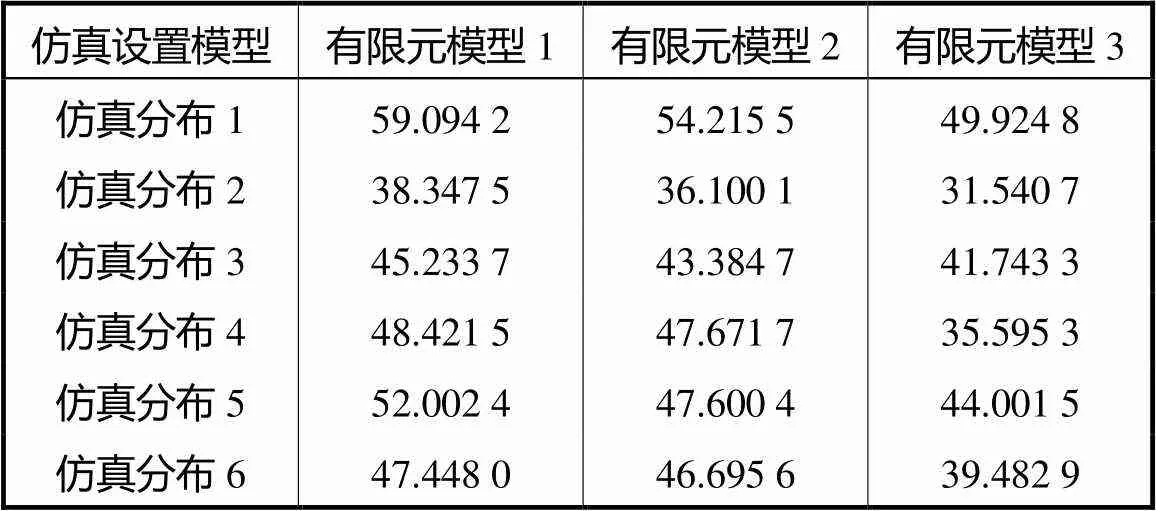
Tab.4 Comparison of image relative errors between dif-ferent models with noise disturbance %,

由表3和表4可知，在相同实验条件下，3种有限元模型相关系数的平均值分别为0.641,9、0.667,1、0.743,8，图像相对误差的平均值分别为48.424,6%,、45.944,7%,、40.381,4%,．与有限元模型1、2相比，本文提出的利用h细化优化灵敏度矩阵对应的有限元模型3相关系数有效提高了图像重建精度，与无噪声干扰时结论相同．

3 实际实验与分析

现利用电阻层析成像系统(如图11所示)，设置3种不同实际模型(如图12所示)，重建结果如图13～图15、表5和表6所示．

图11 电阻层析成像系统

图12 实际设置模型

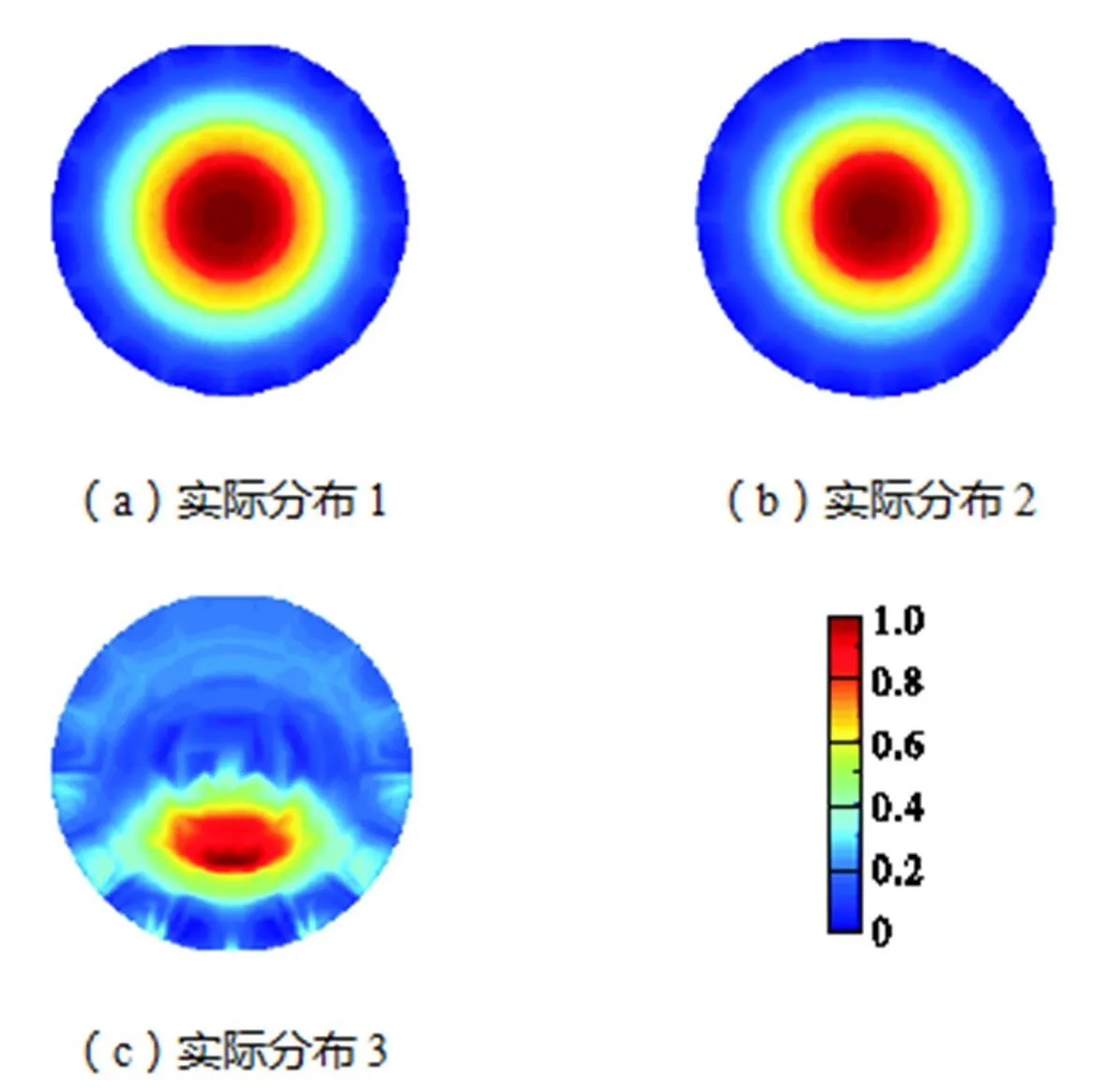
图13 实际设置模型下有限元模型1重建图像

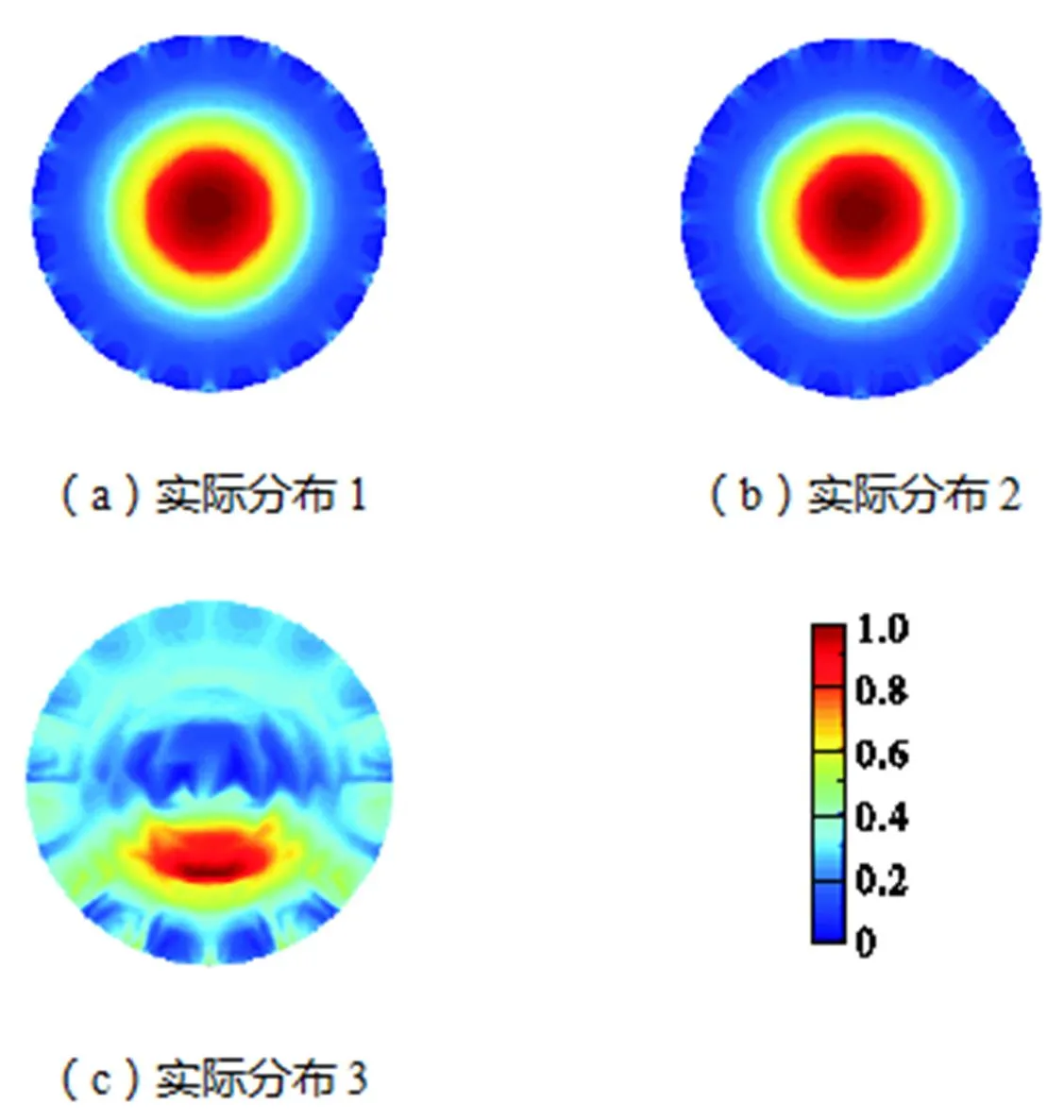
图14 实际设置模型下有限元模型2重建图像

图15 实际设置模型下有限元模型3重建图像

其中软件系统基于Windows平台，编程语言采用C＋＋，操作界面简洁方便，基于OpenGL图像显示(彩色/灰度)，软件包含目前电阻层析成像技术几种常用的图像重建算法，方便二次开发．硬件系统包括模拟信号处理板、数字信号处理板、系统背板以及机箱等．均匀分布在圆桶内壁的阵列电极数目为16，数据采集采取相邻激励模式，圆桶内径、外径分别为18.380,0,cm、19.890,0,cm.在图12实际设置模型中，实际分布1的4号有机玻璃棒与实际分布2的1号有机玻璃棒直径分别为3.525,0,cm、4.015,0,cm，实际分布3的尼龙弦长为16.550,0,cm、高度为5.770,0,cm(有机玻璃棒与尼龙均不导电)，并将加入适量食盐的自来水倒入圆桶内．

表5 实际设置模型下不同模型相关系数比较

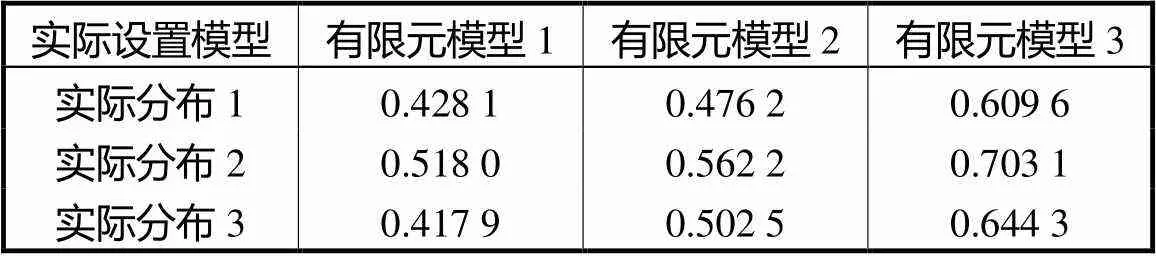
Tab.5 Comparison of correlation coefficients between different models for actual setting models

表6实际设置模型下不同模型图像相对误差比较

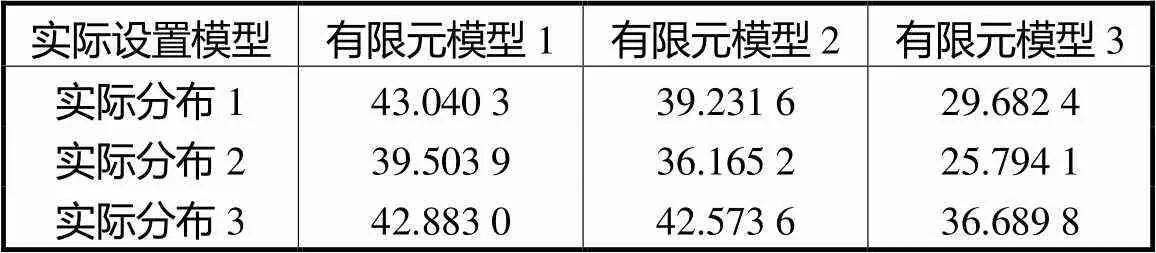
Tab.6 Comparison of image relative errors between dif-ferent models for actual setting models %,

由表5和表6可知，在相同实验条件下，3种有限元模型相关系数的平均值分别为0.454,7、0.513,6、0.652,3，图像相对误差的平均值分别为41.809,1%,、39.323,5%,、30.722,1%,．与有限元模型1、2相比，本文提出的利用h细化优化灵敏度矩阵对应的有限元模型3有效提高了图像重建质量，与仿真实验结论相同．

4 结 语

电阻层析成像逆问题病态的根源是灵敏度矩阵条件数很大．为了提高算法图像重建精度，针对其病态性，本文在可有效提高正问题计算精度的有限元模型基础上，以h细化区域的起始层数、终止层数以及三角形有限元内部所插入节点的横坐标、纵坐标为变量，利用改进粒子群算法h细化有限元模型，以优化敏感场均匀分布时灵敏度矩阵，改善其病态程度(如图1有限元模型3所示)．实验结果表明，本文提出的利用h细化优化灵敏度矩阵有效克服了全局细化有限元模型的不足之处，在不影响算法实时性与正问题计算精度的前提下，有效改善了敏感场均匀分布时灵敏度矩阵的病态程度，并通过改进Landweber预迭代算法，验证了本文提出的利用h细化优化灵敏度矩阵在提高图像重建质量方面的有效性.

［1］ 陈江涛，刘 石. 融合电容层析成像先验信息的集合卡尔曼滤波统计估计[J]. 化学工程，2012，40(4)：36-39.

Chen Jiangtao，Liu Shi. Statistical estimation of ensemble Kalman filter fusion based on priori information approach in electrical capacitance tomography[J].，2012，40(4)：36-39(in Chinese).

［2］ 郭志恒，律德才，邵富群. 基于差分灵敏度模型的电容层析成像图像重建方法[J]. 中国电机工程学报，2012，32(23)：75-82.

Guo Zhiheng，Lü Decai，Shao Fuqun. Image reconstruction method for electrical capacitance tomography based on the difference sensitivity model[J].，2012，32(23)：75-82(in Chinese).

［3］ 王丕涛，王化祥，孙犇渊. 基于内阵列电极的ECT/ERT双模态成像[J]. 天津大学学报：自然科学与工程技术版，2015，48(4)：311-317.

Wang Pitao，Wang Huaxiang，Sun Benyuan. ECT/ERT dual-modality tomography based on inner electrode array [J].：，2015，48(4)：311-317(in Chinese).

［4］ Chen Qi，Liu Shi. Flame imaging in meso-scale porous media burner using electrical capacitance tomography [J].，2012，20(2)：329-336.

［5］ 王莉莉，陈德运，于晓洋，等. 电容层析成像系统传感器优化设计[J]. 仪器仪表学报，2015，36(3)：515-522.

Wang Lili，Chen Deyun，Yu Xiaoyang，et al. Sensor optimization design in electrical capacitance tomography system[J].，2015，36(3)：515-522(in Chinese).

［6］ 刘 靖，王雪瑶，刘 石. 多相流测量用动态电容层析成像图像重建算法[J]. 仪器仪表学报，2015，36(10)：2355-2362.

Liu Jing，Wang Xueyao，Liu Shi. Dynamic image reconstruction method for electrical capacitance tomography in multiphase flow measurement[J].，2015，36(10)：2355-2362(in Chinese).

［7］ 马 敏，王伯波，薛 倩. 基于数据融合的ECT图像重建算法[J]. 仪器仪表学报，2015，36(12)：2798-2803.

Ma Min，Wang Bobo，Xue Qian. ECT image reconstruction algorithm based on data fusion[J].，2015，36(12)：2798-2803(in Chinese).

［8］ Yang W Q，Beck M S，Byars M. Electrical capacitance tomography：From design to applications[J].&，1995，28(9)：261-266.

［9］ 王化祥，黄文瑞，范文茹. 三维电阻抗成像的测量模式[J]. 天津大学学报：自然科学与工程技术版，2012，45(8)：729-734.

Wang Huaxiang，Huang Wenrui，Fan Wenru. Measurement pattern for 3D electrical impedance tomography[J].：，2012，45(8)：729-734(in Chinese).

［10］ 陈晓艳，杨永政，杜 萌. 无解调电阻抗成像方法研究[J]. 传感技术学报，2015，28(6)：870-875.

Chen Xiaoyan，Yang Yongzheng，Du Meng. Non-demodulation method study for electrical impedance tomography[J].，2015，28(6)：870-875(in Chinese).

［11］ 汪剑鸣，李文聪，张荣华，等. 基于最大期望算法的电阻抗成像系统的图像重建[J]. 传感技术学报，2015，28(11)：1652-1658.

Wang Jianming，Li Wencong，Zhang Ronghua，et al. The images reconstruction of electrical impedance tomography by EM method[J].，2015，28(11)：1652-1658(in Chinese).

［12］ Wang Yan，Sha Hong，Ren Chaoshi. Optimum design of electrode structure and parameters in electrical impedance tomography[J].，2006，27(3)：291-306.

［13］ Polydorides N，Lionheart W R B. A Matlab toolkit for three-dimensional electrical impedance tomography：A contribution to the electrical impedance and diffuse optical reconstruction software project[J].，2002，13(12)：1871-1883.

［14］ 董 峰，赵 佳，许燕斌，等. 用于电阻层析成像的快速自适应硬阈值算法[J]. 天津大学学报：自然科学与工程技术版，2015，48(4)：305-310.

Dong Feng，Zhao Jia，Xu Yanbin，et al. A fast adaptive iterative hard threshold algorithm for electrical resistance tomography[J].：，2015，48(4)：305-310(in Chinese).

［15］ Dong Feng，Xu Yanbin. Application of electrical resistance tomography in two-phase flow measurement[J].，2006，27(5)：791-794.

［16］ Daily W，Ramirez A. Electrical resistance tomography [J].，2004，23(5)：438-442.

［17］ 肖理庆，王化祥，邵晓根. 基于模型细化改进牛顿-拉夫逊图像重建算法[J]. 仪器仪表学报，2014，35(7)：1546-1554.

Xiao Liqing，Wang Huaxiang，Shao Xiaogen. Improved Newton-Raphson image reconstruction algorithm based on model refining[J].，2014，35(7)：1546-1554(in Chinese).

［18］ Dickin F，Wang Mi. Electrical resistance tomography for process applications[J].，1996，7(3)：247-260.

［19］ 赵 倩，郝建娜，尹武良. 电磁层析成像系统中标量磁势的数值解法[J]. 天津大学学报：自然科学与工程技术版，2014，47(7)：613-618.

Zhao Qian，Hao Jianna，Yin Wuliang. Numerical approach for the magnetic scalarpotential of electrom-agnetic tomography system[J].：，2014，47(7)：613-618(in Chinese).

［20］ Ma X，Peyton A J，Higson S R，et al. Hardware and software design for an electromagnetic induction tomography(EMT)system for high contrast metal process applications[J].，2006，17(1)：111-118.

［21］ Yin W，Peyton A J. A planar EMT system for the detection of faults on thin metallic plates[J].，2006，17(8)：2130-2135.

［22］ 尹武良，王 奔，王化祥. 电磁层析成像中基于半周期采样的数字解调方法[J]. 天津大学学报，2011，44(12)：1118-1123.

Yin Wuliang，Wang Ben，Wang Huaxiang. Digital demodulation based on half-period sampling in electrom-agnetic tomography[J].，2011，44(12)：1118-1123(in Chinese).

［23］ 刘 泽，薛芳其，杨国银，等. 电磁层析成像灵敏度矩阵实验测试方法[J]. 仪器仪表学报，2013，34(9)：1982-1988.

Liu Ze，Xue Fangqi，Yang Guoyin，et al. Experim-ental measurement method of sensitivity matrix for electromagnetic tomography[J].，2013，34(9)：1982-1988(in Chinese).

［24］ Griffiths H. Magnetic induction tomography[J].，2001，12：1126-1131.

［25］ 张立峰. 电学层析成像激励测量模式及图像重建算法研究[D]. 天津：天津大学电气与自动化工程学院，2010.

Zhang Lifeng. Research on Exciting-Measuring Modes and Image Reconstruction Algorithms for Electrical Tomography[D]. Tianjin：School of Electrical Engineering and Automation，Tianjin University，2010(in Chinese).

［26］ 李守晓，王化祥，范文茹，等. 基于三维模型的改进正则化ERT成像算法[J]. 天津大学学报，2012，45(3)：215-220.

Li Shouxiao，Wang Huaxiang，Fan Wenru，et al. Improved regularization reconstruction algorithm based on 3D model for ERT system[J].，2012，45(3)：215-220(in Chinese).

［27］ 魏 颖，赵进创，王 师，等. 基于RBF神经网络的电阻层析成像算法的研究[J]. 仪器仪表学报，2001，22(4)：369-371.

Wei Ying，Zhao Jinchuang，Wang Shi，et al. Research of the image reconstruction algorithm for electrical tomography based on RBF neural network[J].，2001，22(4)：369-371(in Chinese).

［28］ 陈贵敏，贾建援，韩 琪. 粒子群优化算法的惯性权值递减策略研究[J]. 西安交通大学学报，2006，40(1)：53-56.

Chen Guimin，Jia Jianyuan，Han Qi. Study on the strategy of decreasing inertia weight in particle swarm optimization algorithm[J].，2006，40(1)：53-56(in Chinese).

［29］ 肖理庆，王化祥，厉 丹. 改进Landweber预迭代ERT图像重建算法[J]. 中国电机工程学报，2013，33(23)：118-125.

Xiao Liqing，Wang Huaxiang，Li Dan. Improved Landweber pre-iteration algorithm for ERT image reconstruction[J].，2013，33(23)：118-125(in Chinese).

［30］ Xue Qian，Wang Huaxiang，Cui Ziqiang，et al. Electrical capacitance tomography using an accelerated proximal gradient algorithm[J].，2012，83(4)：1-7.

［31］ 闵 锐，杨倩倩，皮亦鸣，等. 基于正则化正交匹配跟踪的SAR层析成像[J]. 电子测量与仪器学报，2012，26(12)：1069-1073.

Min Rui，Yang Qianqian，Pi Yiming，et al. SAR tomography imaging based on regularized orthogonal matching pursuit[J].，2012，26(12)：1069-1073(in Chinese).

(责任编辑：孙立华)

Optimization of Electrical Resistance Tomography Sensitivity Matrix Using h Refinement

Xiao Liqing1,2，Wang Huaxiang3，Nie Wenyan2

(1．School of Precision Instrument and Opto-Electronics Engineering，Tianjin University，Tianjin 300072，China；2. School of Mechanical and Electrical Engineering，Huainan Normal University，Huainan 232038，China；3．School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China)

In order to enhance image reconstruction quality，the sensitivity matrix was optimized using h refinement to cope with the ill-posedness in electrical resistance tomography．The starting and termination number of layer of the h refinement region，the horizontal and vertical coordinates of the nodes were taken as variables，and the reciprocal of the condition number was designed as the fitness function，and the finite element mesh was optimized using h refinement，which was thereafter applied to image reconstruction using the improved Landweber pre-iteration algorithm．Experimental results show that the ill-posedness is improved effectively，the condition number is reduced by 35.354,3%, and 32.820,4%，comparing to the finite element mesh before and after global refinement，and the quality is improved.

electrical resistance tomography；h refinement；sensitivity matrix；ill-posedness

10.11784/tdxbz201606001

TK39

A

0493-2137(2018)02-0150-09

2016-06-01；

2016-09-01.

肖理庆（1981—  ），男，博士，副教授，lqx1981@tju.edu.cn.

王化祥，hxwang@tju.edu.cn.

国家自然科学基金青年科学基金资助项目(61302122，61401466)；江苏省高校自然科学研究面上项目(15KJB520033，16KJB470017，17KJB510053)；安徽省高校优秀青年人才支持计划项目(gxyq2017060).

the Young Scientists Fund of the National Natural Science Foundation of China(No. 61302122，No. 61401466)，Project of Natural Science Research in Universities in Jiangsu(No.,15KJB520033，No.,16KJB470017 and No.,17KJB510053)，and Outstanding Youth Talent Support Program in Anhui Universities(No.gxyq2017060).