面向组合结构刚度非线性特性的等效模型

陈宏威，向建华，左正兴，何联格



面向组合结构刚度非线性特性的等效模型

陈宏威1，向建华1，左正兴1，何联格2

(1. 北京理工大学机械与车辆学院，北京 100081；2. 重庆理工大学车辆工程学院，重庆 400054)

针对组合结构轴向载荷下呈现的刚度非线性特性难以计算的问题，提出了梁-双弹簧等效计算模型，研究了在包含不同材料垫片的组合结构中螺栓预紧力以及部分几何尺寸对轴向刚度非线性特性的影响．结果表明：采用铝合金垫片时，该连接组合结构的非线性特性主要表现为其轴向载荷-位移曲线在拉压状态改变时出现明显拐点；而该结构采用石墨垫片时，位移曲线在拉压阶段分别表现出非线性．相比于垫片厚度，螺栓预紧力、法兰厚度以及螺栓位置对轴向拉压刚度的影响更显著，且影响规律与所受载荷方向、垫片材料属性有关．

连接组合结构；等效模型；轴向刚度；非线性

作为一种高效的构件连接形式，螺栓连接广泛应用于构件间的紧固[1-2]．螺栓配合垫片使用时，则可以组成组合结构(以下称组合结构)，以满足其密封要求[3]．组合结构在拉压载荷下呈现轴向刚度非线性特性，这将会影响组合结构力学响应特性，进而改变其密封性能．

外力作用下的组合结构的力学响应是一种典型的接触问题，其动力学分析主要分为两个方面：一方面，深入分析接触面之间的接触原理，在此基础上进行定量计算；另一方面，对组合结构(特别是连接部分)中的接触、垫片材料等非线性特性进行简化建模，配合有限元数值解析．在接触面微观接触原理方面，Lima等[4]认为，由于组合结构的几何突变和结构不连续，其动力学响应类似半刚体(semi-rigid)，产生过大的局部变形以及不均匀分布的应力等接触应力不足的情况．张红艳等[5]建立了非线性接触模型和线性固联模型，分析了计及微观接触时螺栓预紧力对减小模型的计算误差作用．Liu等[6]认为应引入横向载荷对轴向接触刚度的影响，并探讨了分形维数对轴向接触刚度的非线性影响．温淑花等[7-8]利用分形接触理论和微接触面积分布函数得到了结合面的法向刚度以及切向刚度的仿真解．在构建简化模型方面，Tinker[9]证明了螺栓-垫片-法兰组合结构的螺栓连接部位是组合结构轴向刚度非线性特性的一个主要来源．张琪昌等[10]等利用ICMCM法修正了初始有限元模型的刚度、质量矩阵．栾宇[11]提出等效弯曲梁-轴向弹簧简化模型，较好地模拟了接触非线性以及法兰材料的非线性特征．黄开放[12]基于虚拟材料法，构建虚拟材料结合面以模拟机匣振动特性．以上研究探讨了螺栓-垫片-法兰组合结构在拉压载荷下存在轴向非线性位移变形，但对其轴向拉压刚度非线性的产生机理及垫片和垫片材料对影响规律的研究开展不够．

本文在文献[11]的基础上，深入考虑垫片材料，将组合结构连接部位等效为梁-弹簧，通过精细FEM模型仿真计算对比，验证了该数学模型，并阐述了组合结构轴向拉压刚度非线性的产生机理及相关因素的影响，为力学响应特性及密封性的工程研究提供了理论支撑．

1 弯曲梁-双弹簧等效模型

1.1 等效模型的建立

根据在轴向载荷下组合结构连接部位的变形特点，给出以下假设和推论[13]：法兰、螺栓和垫片均符合小变形假设；忽略法兰的厚度变化；将法兰沿径向简化为弹性梁，只产生弯曲变形；法兰与垫片之间近似为点接触．本文忽略螺栓弯曲变形以及螺栓与法兰、垫片螺栓孔的接触．

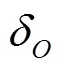
1.2 系统轴向位移及扭转角度分析

轴向拉力作用下，力平衡方程和点弯矩平衡方程分别为

   (1)

   (2)

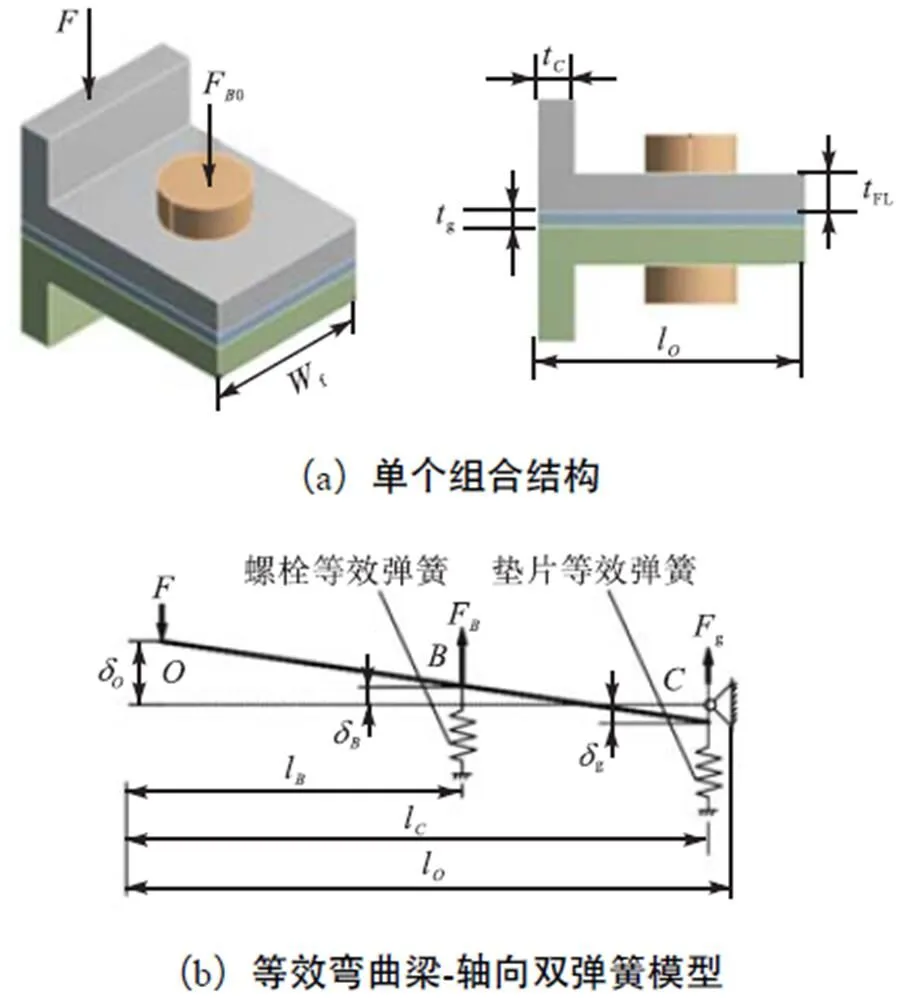
图1 组合结构及其等效模型

位移变形协调条件为

   (3)

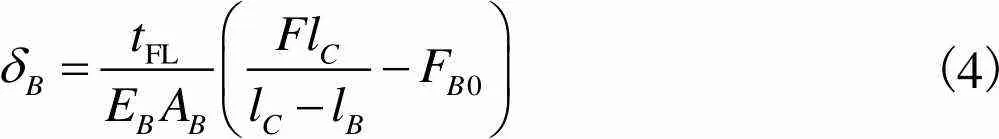
   (4)

     (5)

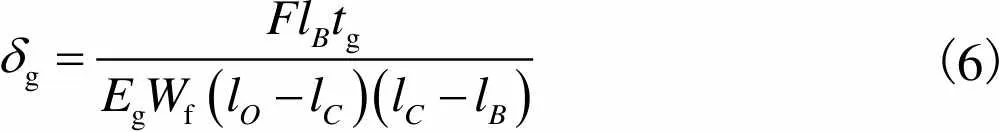
   (6)

基于线弹性小变形的假设，受拉状态下梁自由端的横向位移(即螺栓连接部位法兰的轴向变形)可通过将轴向外力与螺栓力引起的自由端横向变形叠加求得[14]，即

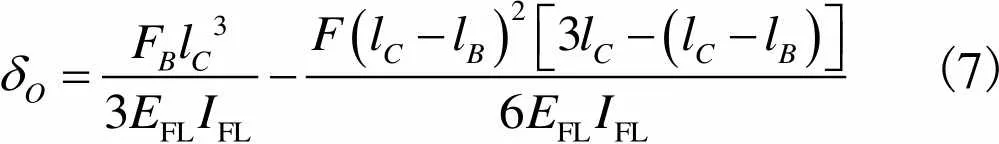
   (7)

受轴向拉载荷时，轴向变形表述为

   (8)

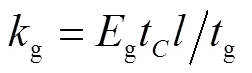
综上，组合结构螺栓连接部位的轴向非线性静力位移响应式可表示为

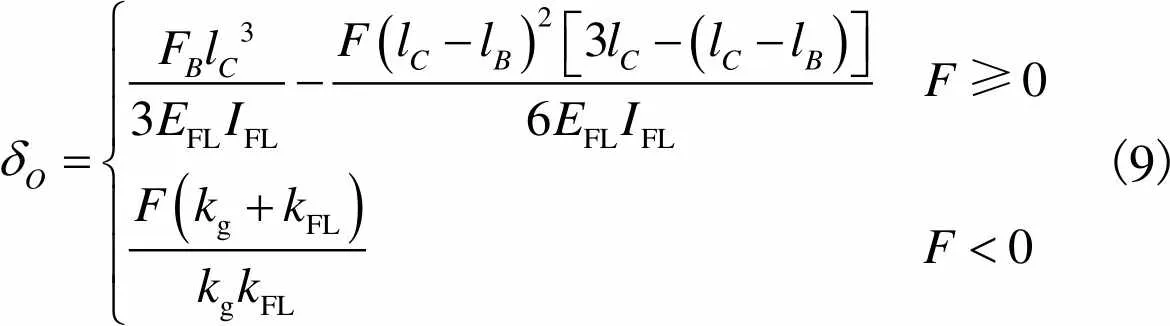
(9)

2 精细有限元模型仿真计算

2.1 垫片材料属性测定

分别考虑铝合金垫片(线弹性材料)及石墨垫片(非线性材料)对组合结构轴向刚度的影响．组合结构各部件及铝合金垫片的部分材料特性见表1．

表1 部件材料特性

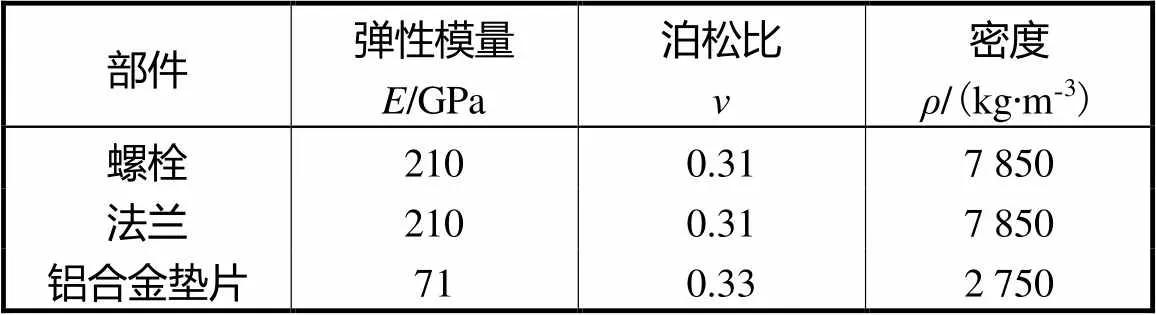
Tab.1 Components material parameter

石墨垫片的压缩回弹特性受材料、加工条件的影响较大，需单独测试(图2)．采用Zwick-5kN静态材料试验机对本文所研究的石墨垫片试样进行弹性测试．拟合垫片压缩/回弹阶段的试验数据，得到不同载荷(30,MPa、60,MPa、90,MPa)作用下垫片材料的压缩和回弹曲线(图3)．

图2 气缸垫材料压缩回弹特性试验

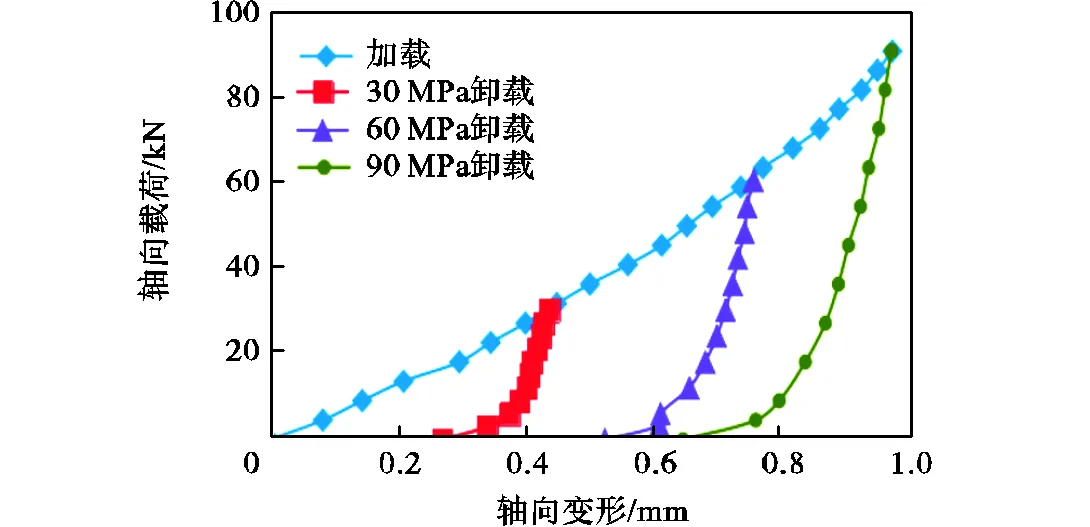
图3 石墨材料垫片压缩回弹特性曲线

2.2 有限元计算及对比计算

计及对称性，提取组合结构中的上侧法兰、螺栓和垫片，建立如图4(a)所示的连接部分精细有限元模型验证结构．模型中各部件之间采用库伦摩擦接触，螺栓螺杆圆柱面上设置预紧单元以施加预紧力．

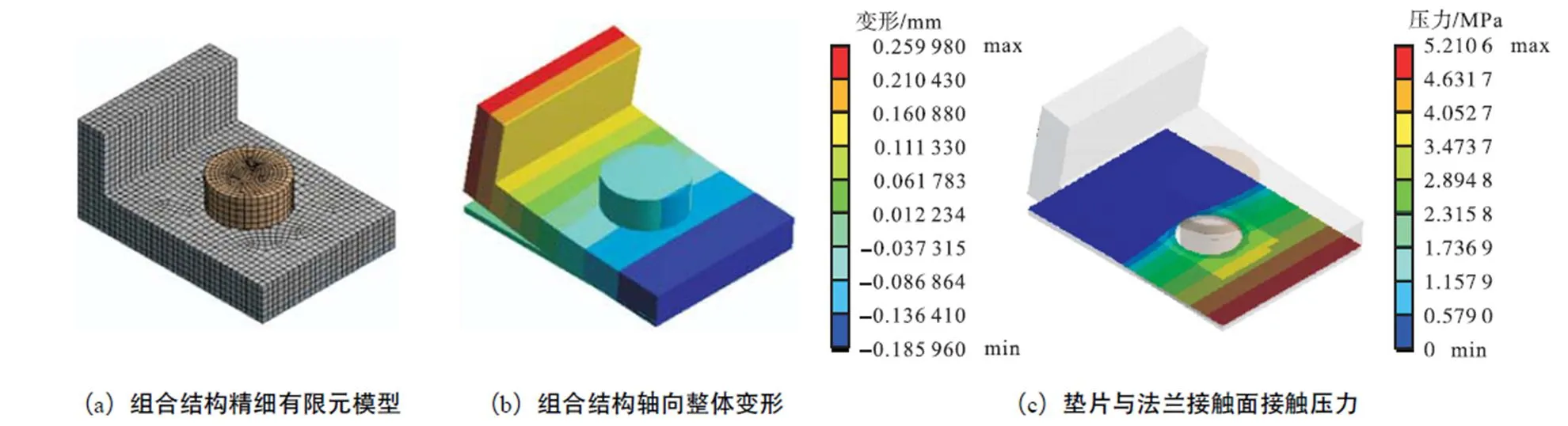
图4 组合结构静力学FEM计算

图5为包含不同垫片材料的组合结构轴向载荷位移曲线．曲线斜率即为轴向刚度．由图5可见，采用不同材料垫片的组合结构表现出不完全相同的轴向刚度非线性特性：①轴向载荷-位移曲线在承受压载荷时的刚度较受拉时明显增大；石墨垫片的组合结构在轴向载荷方向改变时刚度变化较小．这是由于轴向载荷方向改变时组合结构受力面不同，进而导致接触应力的改变，且组合结构中线弹性材料垫片较非线性材料垫片对应力变化更为敏感[15]；②组合结构分别受轴向拉压载荷时，采用线弹性材料垫片的结构轴向刚度均为恒定值，而对于采用非线性石墨材料垫片的组合结构，轴向刚度随载荷变化，这也是组合结构轴向非线性刚度的重要表现．

对比等效模型计算值与精细有限元仿真值还可以看出，等效模型计算值与精密模型解析结果符合较好，故在本文后续分析中采用该等效模型进行研究．

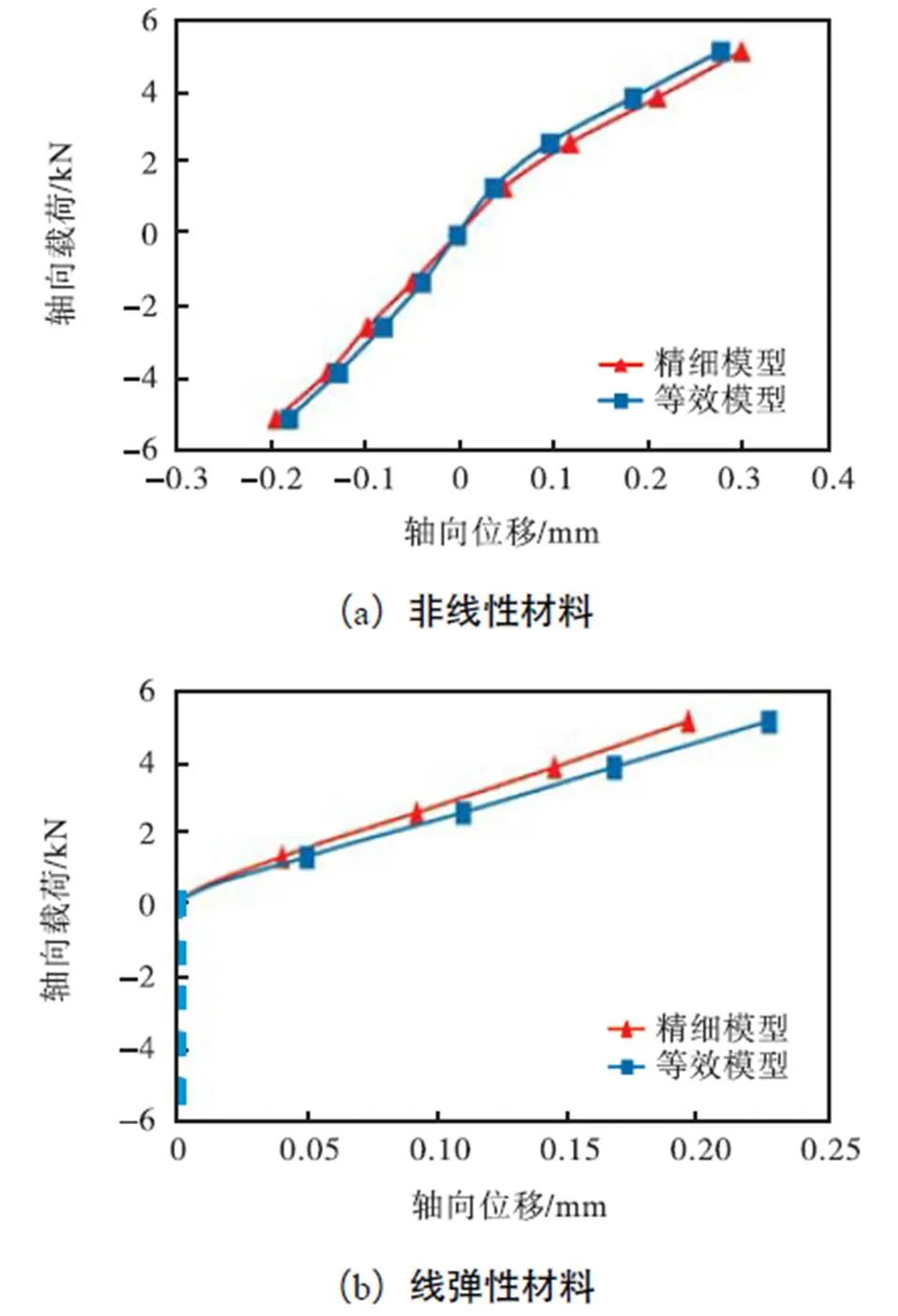
图5 组合结构轴向载荷-位移曲线

3 轴向刚度非线性影响因素分析

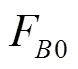
3.1 螺栓预紧力对组合结构轴向刚度的影响

分别取螺栓预紧力5,kN、10,kN和20,kN，计算相应的轴向位移响应，得到不同螺栓预紧力作用下采用不同垫片材料的两种组合结构连接部位轴向载荷-位移曲线(图6)．

由图6可见，在受压载荷阶段，预紧力大小对轴向位移几乎没有影响；在受拉载荷阶段，预紧力对采用不同垫片材料的组合结构轴向拉伸刚度都有较大影响：预紧力越大，组合结构轴向拉伸刚度越大．对比铝合金垫片，在采用石墨垫片的组合结构中，预紧力对轴向拉伸刚度的影响更为明显．

3.2 螺栓位置对组合结构轴向刚度的影响

改变组合结构等效模型的螺栓位置，计算相应的轴向位移响应，得到采用不同垫片材料的两种组合结构螺栓连接部位的轴向载荷-位移曲线(图7)．

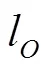
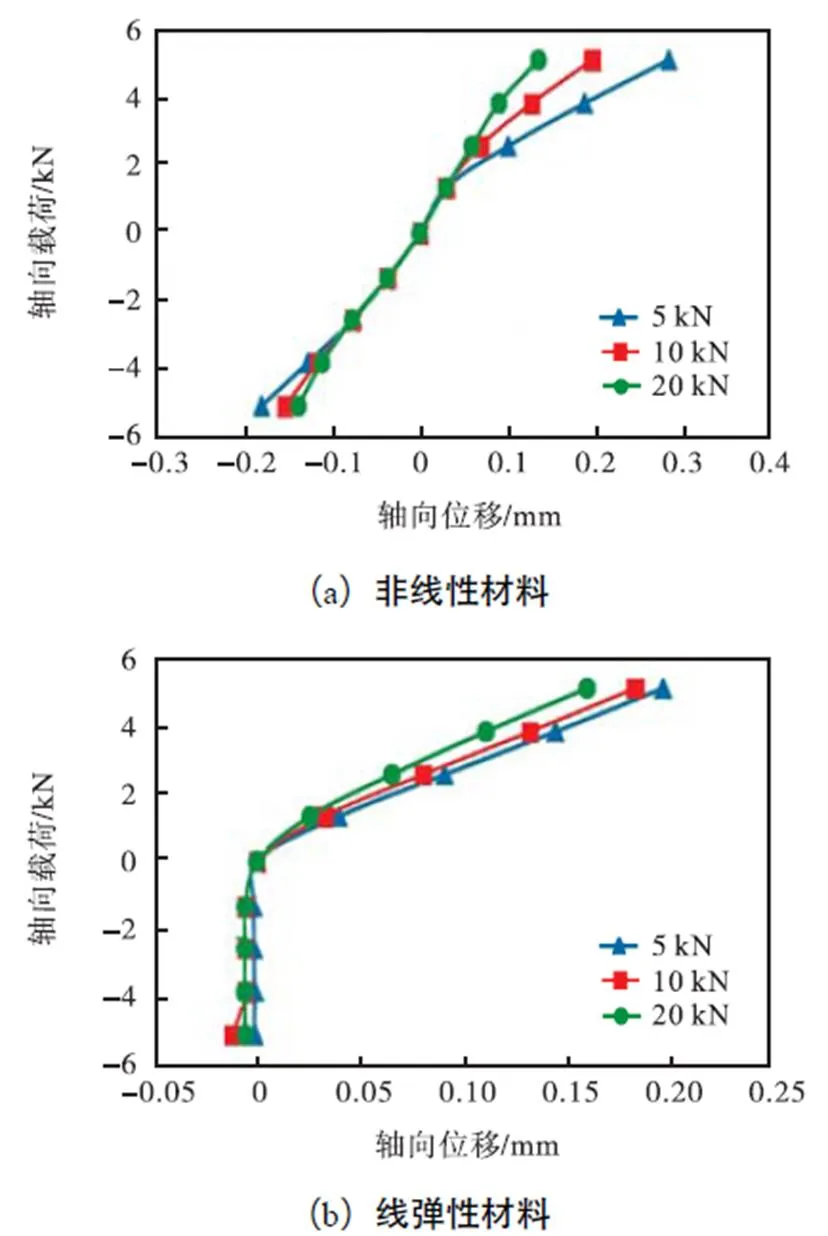
图6 不同螺栓预紧力下的轴向载荷-位移曲线

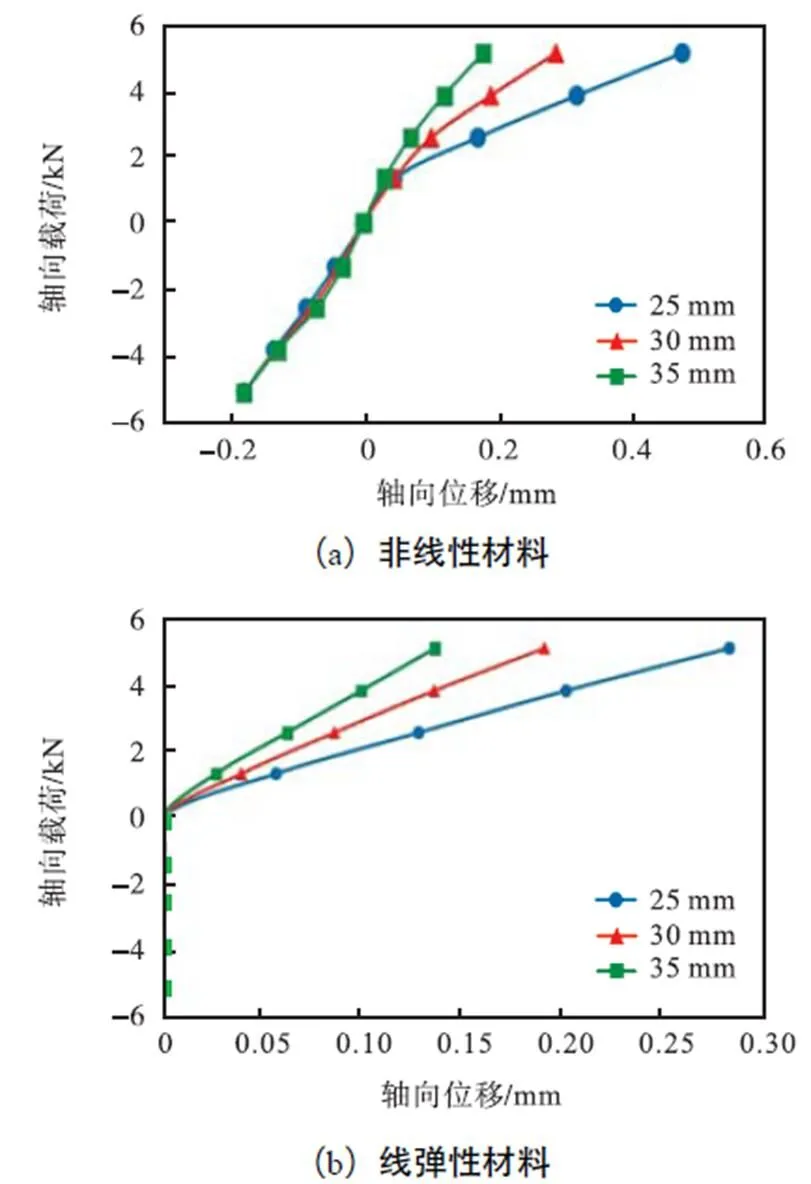
图7 不同螺栓位置下的轴向载荷-位移曲线

3.3 法兰厚度对组合结构轴向刚度的影响

分别取法兰厚度5,mm、10,mm和15,mm，计算相应的轴向位移响应，得到不同法兰厚度对应的采用不同垫片材料组合结构连接部位的轴向载荷-位移曲线(图8)．由图8可见，对于采用铝合金垫片的组合结构，在受拉载荷阶段，法兰厚度与组合结构拉伸刚度均呈正相关．对于采用石墨垫片的组合结构，法兰厚度与组合结构的拉、压刚度均呈正相关，且拉伸刚度受法兰厚度影响更敏感．

图8 不同法兰厚度下的轴向载荷-位移曲线

3.4 垫片厚度对组合结构轴向刚度的影响

由式(6)～(9)可知，垫片厚度将影响组合结构轴向刚度．改变组合结构的垫片厚度，计算相应的轴向位移响应，得到不同垫片厚度对应的采用不同垫片材料组合结构连接部位的轴向载荷-位移曲线(图9)．

由图9可见，在受拉载荷阶段，垫片厚度对轴向位移影响较小．对于采用石墨垫片的组合结构，垫片厚度与组合结构的拉、压刚度均呈负相关，且拉伸刚度受法兰厚度影响更敏感．而采用铝合金垫片时，组合结构拉、压刚度对垫片厚度变化均不敏感．

综上所述，除对石墨垫片组合结构的受压刚度有一定影响外，垫片厚度对铝合金/石墨垫片组合结构刚度影响较小．对于采用铝合金垫片的组合结构，各因素对受压刚度影响也较小；采用铝合金垫片时，组合结构的拉伸刚度受法兰厚度影响较大，而受螺栓位置和螺栓预紧力影响较小．采用石墨垫片时，组合结构的拉压刚度受法兰厚度影响较大，受螺栓位置影响次之，受螺栓预紧力的影响最小．

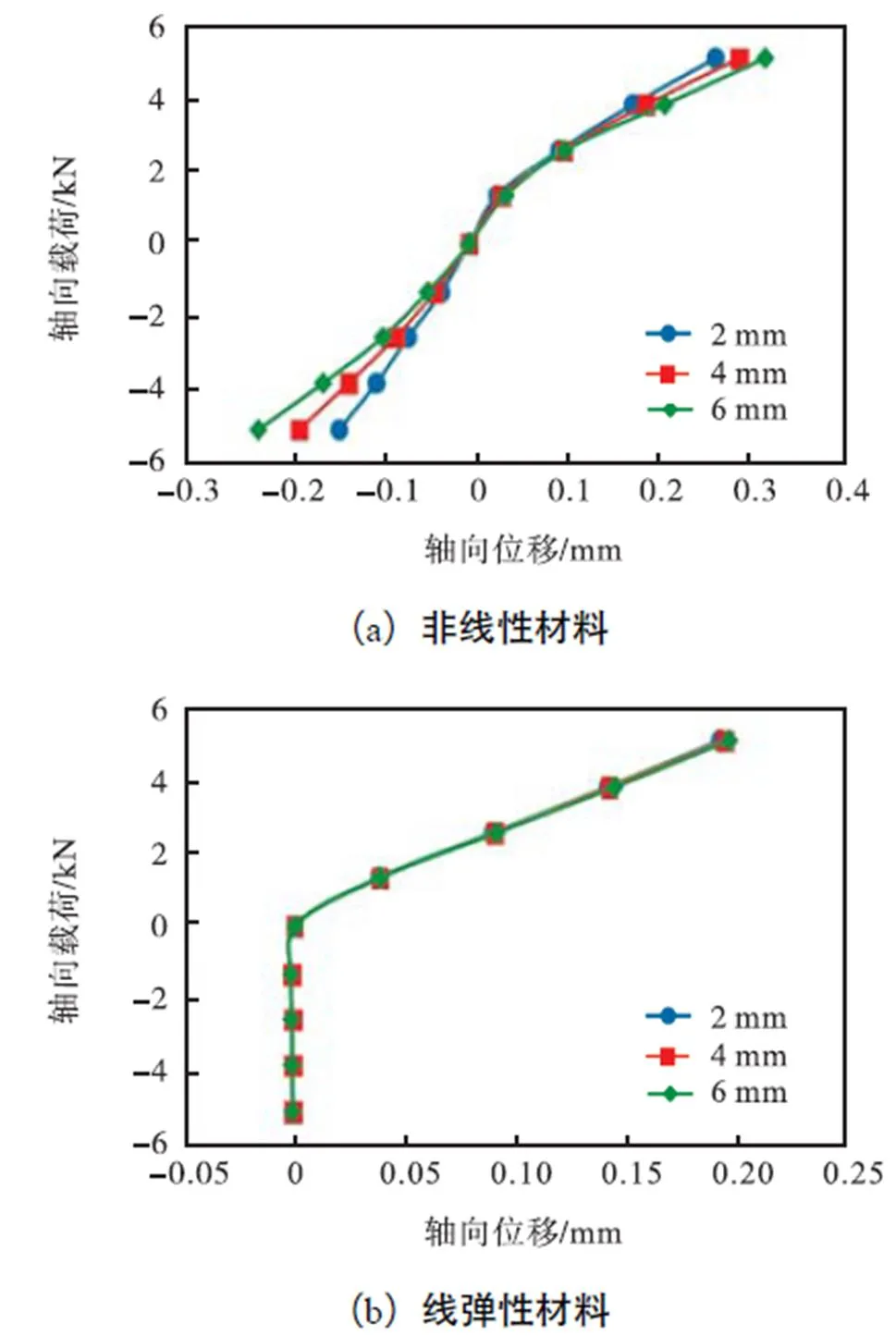
图9 不同垫片厚度下的轴向载荷-位移曲线

4 结 论

(1) 根据垫片-法兰接触面的压力分布以及垫片材料刚度属性，提出了等效弯曲梁-轴向双弹簧模型，并基于组合结构精细模型及等效模型的数值仿真结果进行验证．结果表明，这种等效替代的精确性较好.

(2) 不论垫片采用何种材料，组合结构的轴向载荷-位移曲线在载荷方向改变时均存在拐点．采用线弹性材料时，组合结构的轴向刚度在拐点两侧均为恒定值且数值差别较大；采用非线性材料时，轴向刚度在拐点两侧随载荷变化而变化．

(3) 相比于垫片厚度，法兰厚度、螺栓位置以及螺栓预紧力对组合结构轴向刚度的影响更显著，且其影响规律与载荷方向、垫片材料属性有关．

［1］ 罗永峰，王熹宇，强旭红，等. 高强钢在工程结构中的应用进展[J]. 天津大学学报：自然科学与工程技版，2015，48(增1)：134-141.

Luo Yongfeng，Wang Xiyu，Qiang Xuhong，et al. Progress in application of high strength steel to engineering structures[J].：，2015，48(Suppl 1)：134-141(in Chinese).

［2］ 王元清，罗睿奇，肖建春，等. 负载下焊接加固钢结构端板连接节点承载性能试验[J]. 天津大学学报：自然科学与工程技术版，2015，48(增1)：25-31.

Wang Yuanqing，Luo Ruiqi，Xiao Jianchun，et al. Experiment of welding reinforcement of end-plate connection nodes in steel-structure under loads[J].：，2015，48(Suppl 1)：25-31(in Chinese).

［3］ 祖炳锋，徐玉梁，刘 捷，等. 车用柴油机缸孔变形整体接触多场分步耦合模拟[J]. 天津大学学报，2009，42(11)：1011-1016.

Zu Bingfeng，Xu Yuliang，Liu Jie，et al. Simulation on cylinder bore deformation of automotive disel engines using integral contact multi-field indirect coupling method[J].，2009，42(11)：1011-1016(in Chinese).

［4］ Lima L R O D，Freire J L D F，Vellasco P C G D S，et al. Structural assessment of minoraxis steel joints using photoelasticity and finite elements[J].，2009，65(2)：466-478.

［5］ 张红艳，白长青，林 旭，等. 螺栓连接接触非线性对钢结构动力学特性的影响[J]. 应用力学学报，2015，32(4)：570-574.

Zhang Hongyan，Bai Changqing，Lin Xu，et al. Influence of non-linearity of bolted connection on dynamic characteristics of steel structure[J].，2015，32(4)：570-574(in Chinese).

［6］ Liu P，Zhao H，Huang K，et al. Research on normal contact stiffness of rough surface considering friction based on fractal theory[J].，2015，349：43-48.

［7］ 温淑花，张学良，武美先，等. 结合面法向接触刚度分形模型建立与仿真[J]. 农业机械学报，2009，40(11)：197-202.

Wen Shuhua，Zhang Xueliang，Wu Meixian，et al. Fractal model of normal contact stiffness of joint interfaces and its simulation[J].，2009，40(11)：197-202(in Chinese).

［8］ 温淑花，张学良，文晓光，等. 结合面切向接触刚度分形模型建立与仿真[J]. 农业机械学报，2009，40(12)：223-227.

Wen Shuhua，Zhang Xueliang，Wen Xiaoguang，et al. Fractal model of tangential contact stiffness of jointinterfaces and its simulation[J].，2009，40(12)：223-227(in Chinese).

［9］ Tinker M L. Nonlinearities due to joint friction and clearance in a structural dynamic test figure[C]//USA，1996，90：35-46.

［10］ 张琪昌，耿 岩，王 辰，等. 模型修正技术在螺栓连接结构中的应用探讨[J]. 天津大学学报：自然科学与工程技术版，2014，47(12)：1095-1100.

Zhang Qichang，Geng Yan，Wang Chen，et al. Application of model updating to bolted joint structures[J].：，2014，47(12)：1095-1100(in Chinese).

［11］ 栾 宇. 航天器结构中螺栓-法兰连接的动力学建模方法研究[D]. 大连：大连理工大学机械工程学院，2012.

Luan Yu. Study on Dynamic Modeling of Bolted Flange Connections in Aerospace Structures[D]. Dalian：School of Mechanical Engineering，Dalian University of Technology，2012(in Chinese).

［12］ 黄开放. 螺栓固定结合面动力学建模与影响因素研究[D]. 武汉：华中科技大学机械科学与工程学院，2012.

Huang Kaifang. A Thesis Submitted in Partial Fulfillment of the Requirements for the Degree of Master of Engineering[D]. Wuhan：School of Mechanical Science & Engineering，Huazhong University of Science and Technology，2012(in Chinese).

［13］ Loureiro A，Gutierrez R，Reinosa J M，et al. Axial stiffness prediction of non-preloaded T-stubs：An analytical frame approach[J].，2010，66(12)：1516-1522.

［14］ 侯世远. 螺纹联接松动机理研究[D]. 北京：北京理工大学机械与车辆学院，2015.

Hou Shiyuan. Study on Mechanism of Loosening of Threaded[D]. Beijing：School of Mechanical Engineering，Beijing Institute of Technology，2015(in Chinese).

［15］ Grosse I R，Mitchell L D. Nonlinear axial stiffness characteristics of bolted joints[J].，1990，122：442-449.

(责任编辑：金顺爱)

Non-Linear Characters of Stiffness of Combination Structure Based on Equivalent Model

Chen Hongwei1，Xiang Jianhua1，Zuo Zhengxing1，He Liange2

(1．School of Mechanical Engineering，Beijing Institute of Technology，Beijing 100081，China；2．Vehicle Engineering Institute，Chongqing University of Technology，Chongqing 400054，China)

In the case of different axial loads，a combination structure shows its non-linear axial stiffness，which is hard to calculate．To solve this problem，an equivalent model，bending beam-double springs，was proposed．The influence of bolt pre-tightening force and geometric parameters on the non-linearity of joint axial stiffness of combination structure with different material properties of gaskets was discussed．Results indicate that when aluminum alloy gasket is used，inflection point occurs in axial load-displacement curve between the stages of stress and tension．When graphite gasket is used，displacement curve demonstrates apparent non-linear stiffness in the stages of both stress and tension．Compared with the thickness of the gasket，bolt pre-tightening force，flange thickness and position of the bolt play a more significant role on axial stiffness，and the influence law is related to loading direction and material properties of gasket.

combination structure；equivalent model；axial stiffness；non-linear

10.11784/tdxbz201705022

TH131.3

A

0493-2137(2018)02-0190-06

2017-05-09；

2017-06-29.

陈宏威（1991—  ），男，博士研究生，colin_chenhw@foxmail.com.

向建华，xiangjh@bit.edu.cn.

2017-09-19.

http://kns.cnki.net/kcms/detail/12.1127.N.20170919.0915.002.html.

国家自然科学基金资助项目(51275043).

the National Natural Science Foundation of China(No. 51275043).