计入基础运动的环状周期结构振动特性分析
2018-03-06王世宇赵小雪
王世宇,赵小雪
计入基础运动的环状周期结构振动特性分析
王世宇1, 2,赵小雪1
(1. 天津大学机械工程学院,天津 300350;2. 天津市非线性动力学与控制重点实验室,天津 300350)
研究了一类工程领域广泛应用的环状周期结构的弹性振动特性,重点分析了基础运动对弹性振动稳定性和固有频率分裂的影响.首先在随动坐标系下采用Hamilton原理建立了计入基础运动和面内切向及径向弹性振动的偏微分形式的动力学模型.然后,应用伽辽金方法将其离散得到一组常微分动力学方程.根据经典振动理论,得到了系统特征值的数学表达.最后采用数值方法计算了系统的特征值.根据特征值的实虚部取值预测了不稳定域和固有频率分裂规律,并用Runge-Kutta法给出稳定性的数值验证.该研究为陀螺仪等呈现平面或空间基础运动的环状周期结构的动态性能的改善提供了理论借鉴.
环状周期结构;弹性振动;稳定性;特征值
工程领域广泛应用环状周期结构,例如旋转电机的定转子、行星传动的齿圈以及轴承的内外圈等.在电磁力、啮合力及其他激振力的作用下,构件呈现复杂的振动行为.在基础运动的作用下,动力学响应将变得更为复杂[1].随着现代机械向高速化、轻量化及精密化方向发展,振动问题日益突出.本文拟研究基础运动对环状周期结构的动力稳定性及固有频率分裂的影响.
美国学者Canchi等[2-4]采用多尺度法分别研究了非旋转和旋转圆环的动力稳定性,揭示了基本参数与稳定性之间的映射关系.Zhang等[5]采用摄动法分析了环状周期结构的特征参数与固有频率分裂的关系,并提出一种频率分裂抑制方法.Wang等[6]探讨了分组对称构型周期结构的固有频率分裂规律及其抑制方法,并给出有限元验证.徐进友等[7]采用直接摄动法研究了环状周期结构的动力学特性,给出了由附加子结构个数及振动波数决定的固有频率分裂条件. Zhang等[8]研究了分裂模态处的共振响应规律.应当指出的是,上述研究均未计入基础运动的影响.
在航空航天等呈现空间运动的场合,构件的微幅弹性振动与基础运动耦合,呈现高度复杂的动力学行为.Esmaeili等[9]以陀螺仪为研究对象,建立了复杂的动力学模型,研究了基础运动对动力学行为的影响机理.但是,该文献忽略了基础运动对稳定性的影响.事实上,动力稳定性及模态特性与系统的动态性能密切相关.Yoon等[10]采用拉格朗日方法建立了计入面内弯曲振动和刚体振动的多维动力学模型,分析了振动对输出特性的影响,还探讨了制造误差和对称性与振动模态的关系及其对陀螺仪误差的影响.但是,该文献仅研究了基础的定轴转动情形.考虑实际运动形式的复杂性,应该计入更多因素以精确预测动力学行为.张薇薇等[11]计入基础运动的影响,建立了磁悬浮轴承-转子-基础系统的机电耦联动力学模型,分析了动力学性能.但是该文献仅考虑了平面基础运动.文献[1]运用有限元和拉格朗日方法建立了舰船汽轮机转子系统的动力学模型,研究了基础绕横轴定速旋转和绕纵轴的简谐运动对临界转速和轴心轨迹的影响.受应用场合限制,该文献将涡轮和压气机简化为圆盘结构.文献[12]以陀螺仪为背景建立了圆环模型,分析了振动稳定性,结果表明固有频率分裂、激励力和阻尼系数均影响零点偏移.应当指出的是,该研究仅针对驻波响应.
本文拟研究基础运动对环状周期结构动力稳定性及固有频率分裂的影响.首先在随动坐标系下建立含空间旋转运动的偏微分动力学模型.然后采用Galerkin离散[13]得到常微分模型,应用解析和数值方法计算特征值,并根据特征值预测基本参数对动力稳定性及固有频率分裂的影响规律.最后采用数值计算验证结论的正确性.
1 数学建模
1.1 模型描述
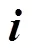

图1 环状周期结构及坐标系
1.2 数学建模
前人通常采用能量法建立弹性结构动力学模 型[3, 4, 14-16],该方法规范、高效,易于保证正确性.为此,本节采用能量法在图1(a)和(b)所示惯性坐标系和随动坐标系下建模.将中性线上的任意点0的位置矢量表示为

(1)
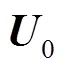
在随动坐标系下,有

(2)

(3)
式中:x和y分别为点0的横、纵坐标;0x和0y分别为随动坐标系中和轴的振动位移分量.
将随动坐标系的角速度表示为

(4)
随动坐标系原点的速度可表示为

(5)
0点的速度可表示为
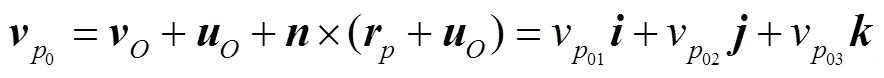

取速度点积

(7)
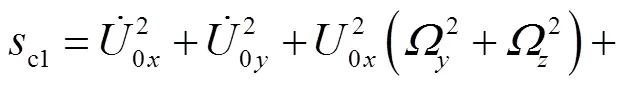
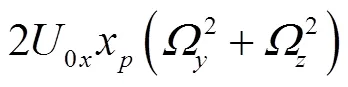
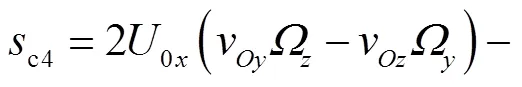
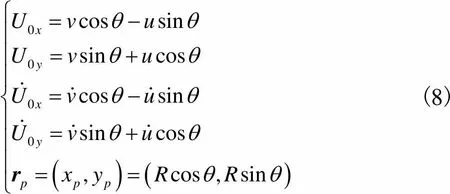
(8)
式中、和分别为0点在极坐标系下的切向位移、径向位移和位置角.
将式(8)代入式(7),可得
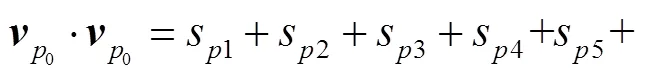
(9)
式中

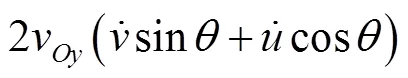
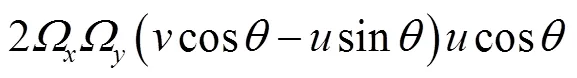
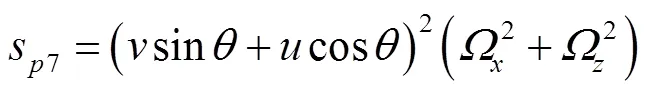
系统的动能可表示为

(10)
根据薄环假设,切向应变可表示为[17]

(11)
其中
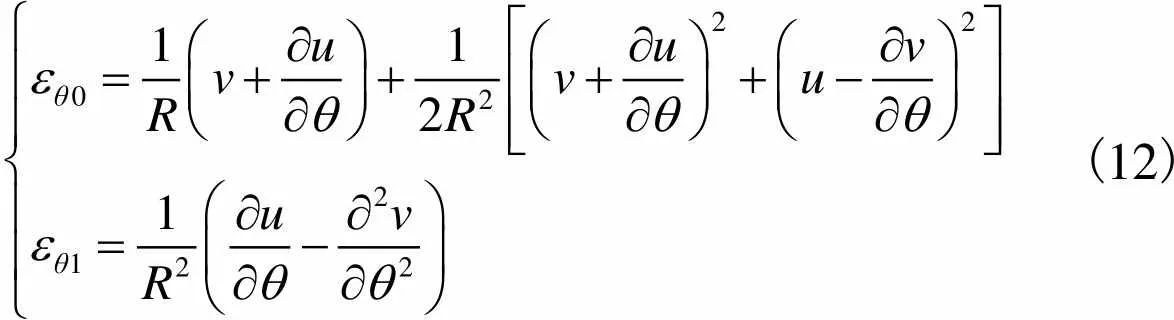
(12)
面内弯曲产生的弹性势能为
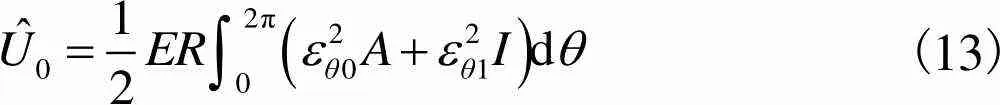
(13)
式中:为截面积,=;为截面惯性矩,=3/12.离散支撑的弹性势能为
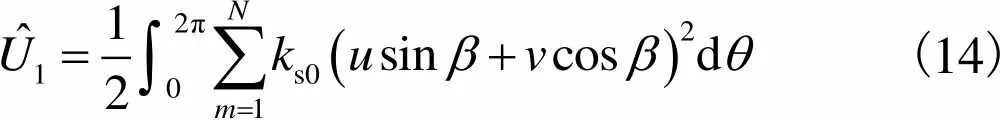
(14)
均布支撑的弹性势能为
总势能为

(16)
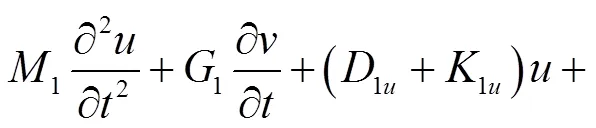

(17)

(18)
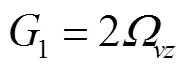
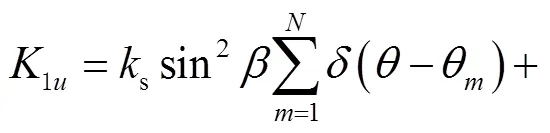

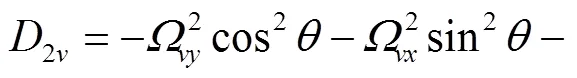

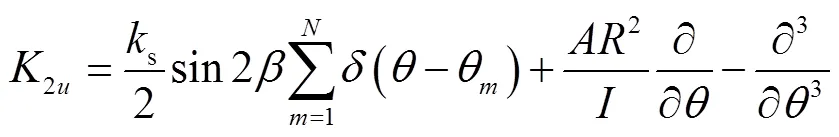
2 模型求解
采用Galerkin方法[13]离散式(17)和(18),假设
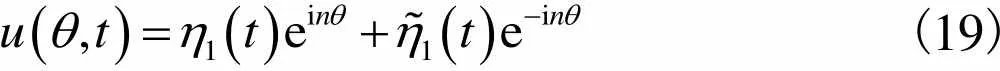
(19)
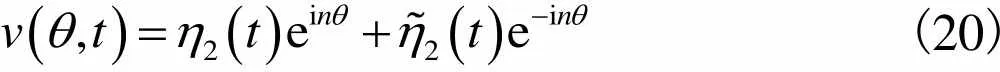
(20)

定义内积

(21)
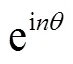

(22)
其中



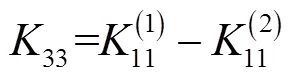

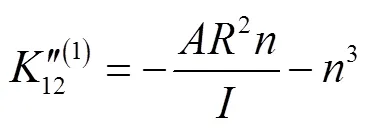


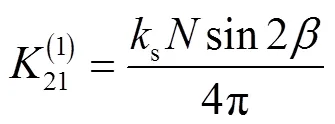

为了确定式(22)的特征值,引入变换

(23)
则式(22)可写为

(24)

(25)

(26)
可采用经典振动理论求解式(26)的特征值,然后预测动力稳定性.根据三角函数的运算特性,有
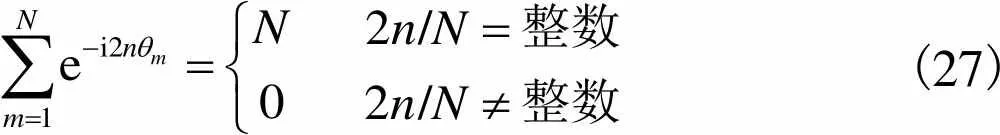
(27)
根据式(26)和(27)可分析波数和离散支撑个数等基本参数对特征值的影响规律,进而揭示基本参数与稳定性及固有频率分裂的映射关系.本文仅研究式(27)中的第1种情形.
3 仿真计算
图3描述了不同基础运动条件下不稳定域随径向和切向刚度的变化规律,图中阴影区域表示不稳定.图3表明绕轴的转动比绕轴的转动更易引起不稳定,而且基础运动形式越复杂,不稳定域越大.图4(a)和(b)给出了不稳定域随径向刚度和绕轴转速的变化规律,图4(c)和(d)给出了不稳定域随径向刚度和绕轴转速的变化规律.图4表明基础旋转速度越大,则不稳定域越大,而且绕不同轴的转动对不稳定区域的影响具有叠加性.
表1 环状周期结构的基本参数

Tab.1 Specifications of a ring-shaped periodic structure
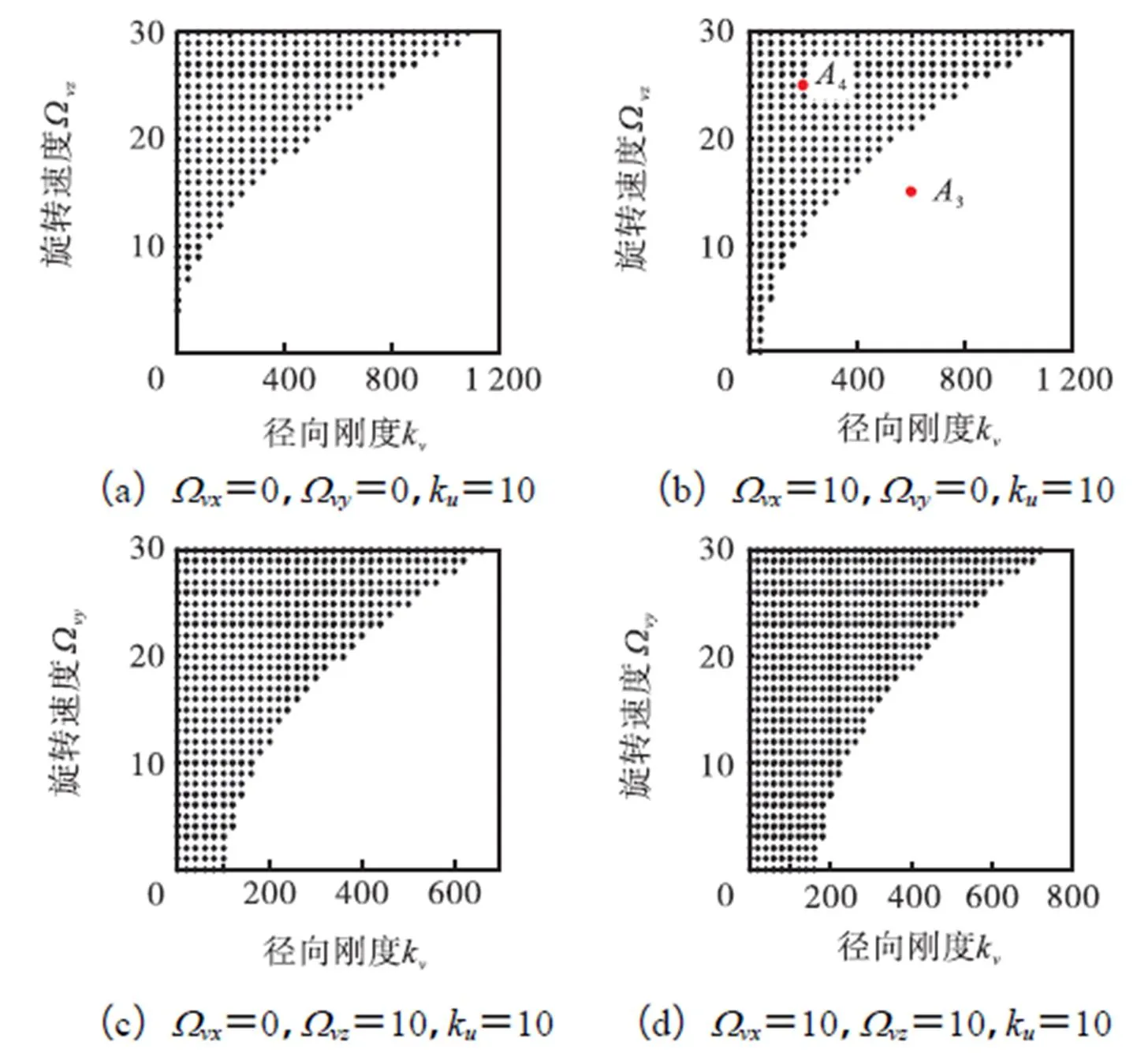
图4 不稳定域随径向刚度和旋转速度的变化规律
图5(a)描述了不稳定域随和轴转速的变化规律.图5(b)描述了不稳定域随和轴转速的变化规律.图5(c)和(d)给出了转速不变时支撑刚度对稳定性的影响.从图5可以看出,绕和轴的转动对不稳定域的影响呈现对称性,该结论与文献[1]一致.与之相反,绕和轴的转动对系统不稳定域的影响没有对称性,而且若转速恒定,则增大径向和切向刚度可增加系统的稳定性.该结论在图3和图4中也有所体现.事实上,在工程实际中刚度不可能无限增大,因此必须合理匹配参数,以期获得良好的综合性能.

图5 不稳定域随旋转速度的变化规律
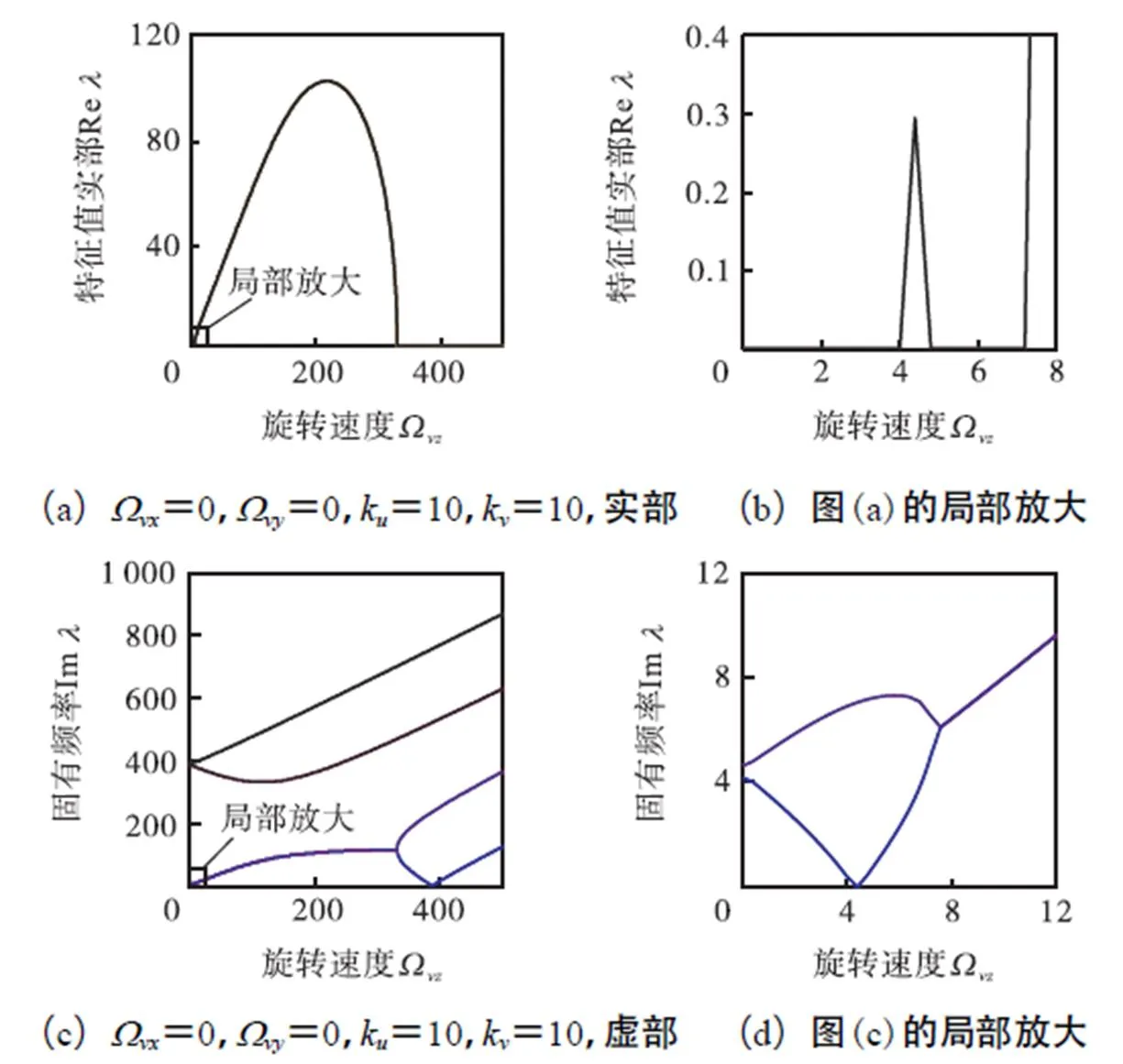
在图6中,(a)、(c)、(e)和(g)给出了特征值随转速的变化规律,其余各图为局部放大.其中,图6(a)描述了实部随轴转速的变化趋势,反映了当前参数下的不稳定域分布.图6(c)为固有频率随轴转速的变化规律.在图6(c)中,上面2支为高阶固有频率,其他为低阶固有频率.图6(c)和(d)表明,对于低阶固有频率,若仅存在轴转动且速度逐渐增加,将出现固有频率先分裂,然后退化,最后再分裂现象,这与非旋转结构和受参激作用的旋转周期结构的固有频率分裂规律有所不同.由于绕或轴转动对动力学特性影响呈现对称特征,本节仅研究前者对固有频率的影响.图6(e)描述了特征值实部随轴转速的变化规律.图6(g)和(h)描述了固有频率随轴转速的变化规律,表明当仅存在绕轴的旋转时,低阶固有频率随转速增加出现退化现象.该结果对合理选择环状构件的最优工作区间有参考价值.对比图6(c)、(d)与(g)、(h)可知,旋转轴不同,则频率分裂规律也有所不同.


4 数值验证
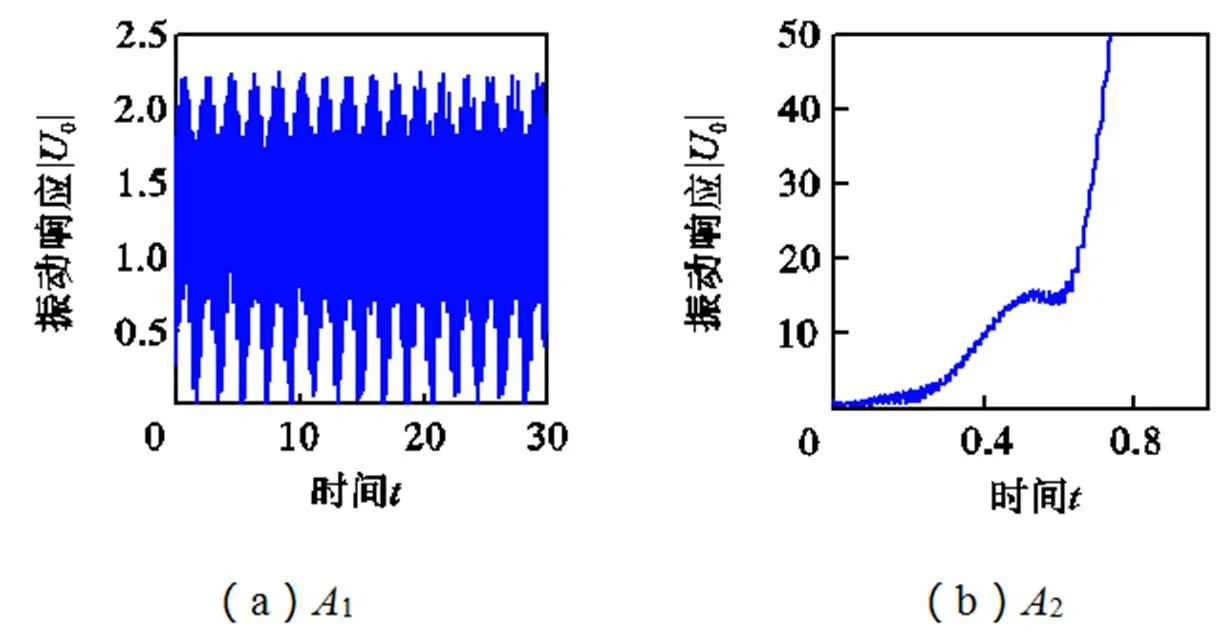
以图3(d)、4(b)和5(a)为例,分别在稳定和不稳定域内选取参数,采用Runge-Kutta方法计算响应,可得图8所示结果.不失一般性,图中取环状结构中性线上位置角为π/6的点给出响应.图8(a)和(b)分别为图3(d)中稳定点(1)和非稳定点(2)的响应;图8(c)和(d)分别为图4(b)中稳定点(3)和非稳定点(4)的响应;而图8(e)和(f)分别对应图5(a)中稳定点(5)和非稳定点(6)的响应.图8(a)和(b)的三轴转速均取为10.图8(a)的切向刚度为300,径向刚度为200.图8(b)的切向和径向刚度均为100.可以看出,图8(a)为周期响应,表明1确实为稳定点,而图8(b)为非周期响应,表明2确实为不稳定点,该结论与图3(d)一致.图8(c)和(d)中的和轴转速及切向刚度分别为10、0和10.其中,图8(c)的径向刚度为600,轴转速为15,而图8(d)的相应参数值分别为200和25.其中,图8(c)为周期响应,表明3点稳定,图8(d)为非周期响应,表明4点非稳定,该结论与图4(b)一致.图8(e)和(f)中的切向刚度、径向刚度和轴转速分别为10、10和0.图8(e)的和轴转速均为2,图8(f)的和轴转速分别为9和8.显然,图8(e)为周期响应,幅值较小,表明5点稳定,而图8(f)为非周期响应,其幅值随时间无限增大,呈现显著的不稳定特征,表明6点非稳定.上述结果验证了图5(a)的正确性.同理可验证图3~图5中其他结果的正确性.篇幅所限,本文不再给出.
5 结 论
(1)采用能量法在随动坐标系下建立了弹性动力学模型.该模型计入了绕3个坐标轴的旋转运动和面内径向及切向弹性振动.
(2) 采用经典振动理论计算了系统的特征值,并据此预测了动力稳定性及固有频率的分裂规律.
(3) 基础运动可导致动力不稳定,而且与定轴旋转结构相似,仍然存在固有频率分裂现象.
(4) 采用数值方法计算了振动响应,验证了基于特征值方法的动力稳定预测结果的正确性.
[1] 张 欢. 考虑基础运动的转子系统动力学特性分析[D]. 哈尔滨:哈尔滨工业大学航天学院,2014.
Zhang Huan. Dynamics Characteristics Analysis of a Rotor System Subject to Base Excitations[D]. Harbin:School of Astronautics,Harbin University of Technology,2014(in Chinese).
[2] Canchi S V,Parker R G. Effect of ring-planet mesh phasing and contact ratio on the parametric instabilities of a planetary gear ring[J].,2008,130:014501-1-014501-6.
[3] Canchi S V,Parker R G. Parametric instability of a circular ring subjected to moving springs[J].,2006,293(1/2):360-379.
[4] Canchi S V,Parker R G. Parametric instability of a rotating circular ring with moving,time-varying springs [J].,2006,128(1/2):231-243.
[5] Zhang D S,Wang S Y,Liu J P. Analytical prediction for free response of rotationally ring-shaped periodic structures[J].,2014,136:041016-1-041016-12.
[6] Wang Y Y,Wang S Y,Zhu D H. Dual-mode frequency splitting elimination of ring periodic structures via feature shifting[J].,2016,230(18):3347-3357.
[7] 徐进友,刘建平,王世宇,等. 环状旋转周期结构模态摄动分析[J]. 天津大学学报,2010,43(11):1015-1019.
Xu Jinyou,Liu Jianping,Wang Shiyu,et al. Modal perturbation analysis for annular rotationally periodic structures[J].,2010,43(11):1015-1019(in Chinese).
[8] Zhang D S,Wang S Y. Spatial-dependent resonance mode and frequency of rotationally periodic structures subjected to standing wave excitation[J].,2017,94:482-498.
[9] Esmaeili M,Durali M,Jalili N. Ring microgyroscope modeling and performance evaluation[J].,2006,12(5):537-553.
[10] Yoon S W,Lee S W,Najafi K. Vibration sensitivity analysis of MEMS vibratory ring gyroscopes[J].:,2011,171:163-177.
[11] 张薇薇,胡业发. 磁力轴承-转子-基础系统的耦合动力学分析[J]. 机械制造,2009,47(534):4-6.
Zhang Weiwei,Hu Yefa. Coupling dynamics analysis of magnetic bearing-rotor-foundation system[J].,2009,47(534):4-6(in Chinese).
[12] Xi X,Wu Y L,Wu X M,et al. Investigation on standing wave vibration of the imperfect resonant shell for cylindrical gyro[J].:,2012,179:70-77.
[13] 胡海岩. 应用非线性动力学[M]. 北京:航空工业出版社,2000.
Hu Haiyan.[M]. Beijing:Aviation Industry Press,2000(in Chinese).
[14] Wu X H,Parker R G. Vibration of rings on a general elastic foundation[J].,2006,295(1/2):194-213.
[15] Wang S Y,Sun W J,Wang Y Y. Instantaneous mode contamination and parametric combination instability of spinning cyclic symmetric ring structures with expanding application to planetary gear ring[J].,2016,375:366-385.
[16] Xia Y,Wang S Y,Sun W J,et al. Analytical estimation on divergence and flutter vibrations of symmetrical three-phase induction stator via field-synchronous coordinates[J].,2016,386:407-420.
[17] Huang S C,Soedel W. Effects of Coriolis acceleration on the free and forced in-plane vibration of rotating rings on elastic foundation[J].,1987,115(2):253-274.
(责任编辑:金顺爱)
Vibration Characteristic Analysis of Ring-Shaped Periodic Structure Incorporating Basic Movement
Wang Shiyu1, 2,Zhao Xiaoxue1
(1.School of Mechanical Engineering,Tianjin University,Tianjin 300350,China;2.Tianjin Key Laboratory of Nonlinear Dynamics and Control,Tianjin 300350,China)
The elastic vibration characteristic of a ring-shaped periodic structure intensively used in engineering practice was examined,where the focus was on the effect of basic movement on elastic vibration stability and natural frequency splitting.Firstly,a partial differential dynamic model incorporating basic movement and in-plane tangential as well as radial elastic vibrations was established in moving frame using Hamilton's principle.Then,a set of ordinary differential dynamic equations were formulated using Galerkin method.The mathematical expressions of eigenvalues of the system were derived according to the classical vibration theory.Finally,the eigenvalues were calculated by use of numerical method.Unstable areas and the rules of natural frequency splitting were predicted by means of real and imaginary parts of eigenvalues.The stability was verified by numerical calculation with Runge-Kutta method.This research provides theoretical reference for the dynamic performance improvement of microgyroscope or other ring-shaped periodic structures undergoing two- or three-dimensional basic movement.
ring-shaped periodic structure;elastic vibration;stability;eigenvalue
10.11784/tdxbz201704045
TH113.1
A
0493-2137(2018)02-0167-08
2017-04-14;
2017-06-03.
王世宇(1974— ),男,博士,副教授.
王世宇,wangshiyu@tju.edu.cn.
国家重点基础研究发展计划(973计划)资助项目(2013CB035403);国家自然科学基金资助项目(51175370,51675368);天津市应用基础与前沿技术研究计划重点资助项目(13JCZDJC34300);天津市应用基础与前沿技术研究计划资助项目(14JCYBJC18800).
the National Basic Research Program of China(No.,2013CB035403),the National Natural Science Foundation of China (No.,51175370 and No.,51675368),the Tianjin Key Research Program of Application Foundation and Advanced Technology (No.,13JCZDJC34300)and the Tianjin Research Program of Application Foundation and Advanced Technology (No.,14JCYBJC18800).
