联合TOA和DOA的浅海多径定位算法

刘开华，魏冲冲，于洁潇



联合TOA和DOA的浅海多径定位算法

刘开华1，魏冲冲1，于洁潇2

(1. 天津大学微电子学院，天津 300072；2. 天津大学电气自动化与信息工程学院，天津 300072)

针对海水媒质分布不均匀的特性，本文提出了一种在非均匀媒质中联合到达时间(TOA)和到达角度(DOA)浅海多径环境下的定位算法．该算法不仅能够克服声速变化引起的路径弯曲问题，还可以减少海水流动对节点拓扑结构产生的影响．首先分别以海面和海底为反射面建立锚节点的虚拟节点(VN)，把多径环境下的非视距(NLOS)问题转化为视距(LOS)问题，然后根据声速剖面(SSP)利用费马原理获得声波曲线路径的表达式．又由于海面、海底形状的不规则性，信号在反射点发生散射现象，因此将反射点当作分布式信源，利用散射信号中心波达方向作为DOA，平均波达时间作为TOA．最后利用到达时间和到达角度估计目标的位置参数．仿真结果表明，本方法在定位精度和鲁棒性等方面优于传统的直线传输模型．

非均匀媒质；多径；声音速度剖面；费马原理；虚拟节点

近年来，水声传感器网络(underwater acoustic sensor network，UASN)在海洋环境监测、海底资源探索、灾难预警监测等方面应用越来越广泛[1-2]．在UASN中，通常把传感器节点布置在一定区域内来获取温度、压力等相关数据，传感器的位置信息将有助于这些数据的分析．因此，节点的位置获取起到了至关重要的作用．

在浅海定位过程中，信号传输经海面和海底反射，产生多径现象，对通信质量造成影响，由此水下多径问题一直是研究的热点方向．室内环境的多径问题已经得到了广泛的研究，但由于水下环境中声速传播慢、节点的移动性以及传播媒质的不均匀性等特点[3-5]，使得原有的室内定位算法在水下不再适用．文献[6]利用自相关和互相关器对TDOA进行估计，之后根据线性最小二乘估计目标的深度和距离．文献[7]用矢量传感器接收多径环境下不同信道传输的信号，获取因水下信道参数不同而带来的矢量传感器阵列的相关性等级差异．文献[8]用同态解卷恢复水下信道的链路信息，根据链路的不同特征对视距和非视距路径做分类，利用闭合形式的最小二乘方法定位目标节点．然而，以上文献使用多锚节点定位，均未考虑海水的流动性对拓扑结构以及定位效果产生的影响[9]，且在UASN中为了降低能量损耗，传感器的布置密度较低，因此仅用一个锚节点定位在真实的UASN中更加合理．

海水的非均匀性还会导致声音速度在不同水深发生变化，从而使得信号传播路径发生弯曲[10-11]，因此在变声速的海洋环境中传统的直线传播模型会加大目标的定位误差．文献[12]分析了同一时间延时和同一速度模型下直线模型和曲线模型的定位表现．文献[13]分析了等梯度速度刨面(sound speed profile，SSP)下的定位情况．之后，文献[14]分析了在多个梯度层下的定位误差．文献[15]根据海水深度信息和声速剖面图估计出水下声波传播时间和传播距离关系，建立了查询表．文献[16]在非均匀的水下媒质中分析了声波传输损失，并且利用接收信号强度RSS估计两点之间曲线距离．文献[17]利用分层补偿的方法处理海水分层效应，之后通过牛顿-拉普森迭代算法求解曲线路径下目标源的位置．

本文将曲线传输模型应用到水下多径环境中，提出了一种在非均匀媒质中联合TOA和DOA的水下多径环境下的定位算法，且该算法仅用一个锚节点即可完成定位．首先利用几何学的方法建立锚节点的虚拟节点(virtual node，VN)，构建虚拟直射路径，然后根据声速模型利用费马原理求出曲线传输路径，最后利用锚节点测到的多条路径到达时间和到达角度估计目标的位置坐标．仿真结果表明，该定位算法在定位精度上优于传统的直线模型算法，并且这种优势随着目标距离的增大而更加明显．

1 数据模型

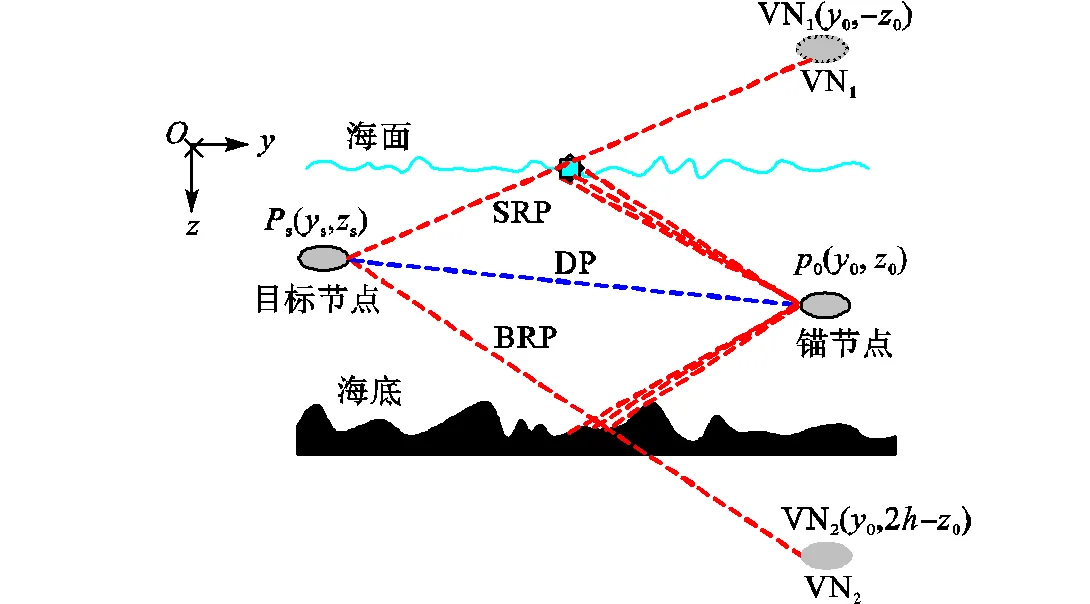
图1 水下节点分布示意

信号在反射面反射时，由于海底和海面的不规则性，反射后的信号会出现一簇散射多径，因此可把海面和海底的反射点等效为分布式信源．鉴于信号的分布对称特性，取中心波达方向作为到达角[18]；又因同一簇的不同散射信号具有近似相同的波达时间，故取一簇散射信号波达时间的均值为信号到达时间[19]，估计参数表示为

   (1)

   (2)

海洋环境声音速度剖面对于定位精度起到了至关重要的作用．本文使用文献[20]中的速度模型进行分析，如图2(a)所示，虚拟节点所处空间的速度模型关于对称面对称，如图2(b)所示．

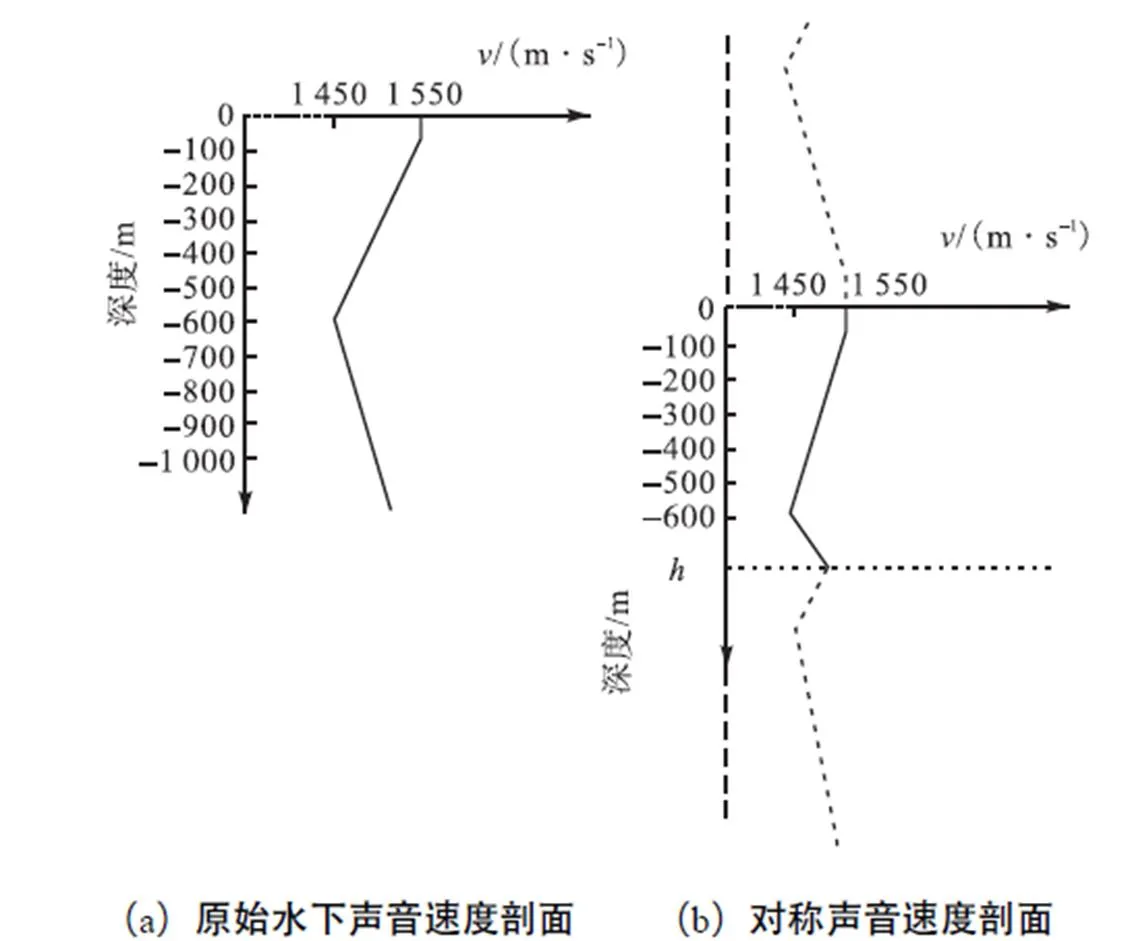
图2 水下声音速度随深度变化剖面

2 基于曲线路径传输的定位算法

2.1 算法流程

本文目标节点定位算法流程如算法如下．

for＝1 to 3 do

end

步骤2 根据锚节点及建立的虚拟节点位置分别获取目标节点的位置坐标．

for＝1 to 3 do

end

步骤3 赋予不同坐标信息不同的权重，并进行融合．

2.2 基于TOA/DOA的联合定位算法

在建立虚拟节点，引入虚拟直射路径之后，对于每条路径分析过程相同，故以DP为例进行分析．定位示意如图3所示．

信号沿曲线传输的真实时间可由曲线积分得到

   (3)

   (5)

   (6)

   (7)

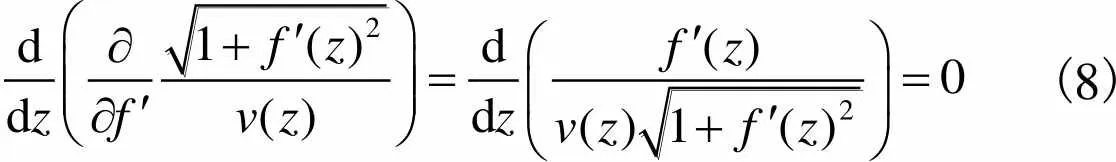
 (8)

即上式的原函数是一个常数，用公式表示为

   (9)

转换形式为

   (10)

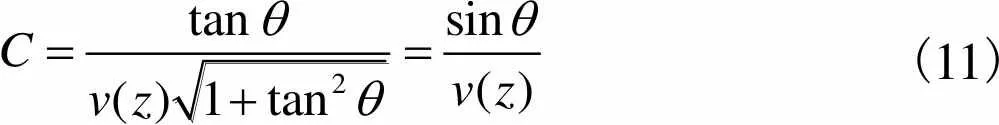
   (11)

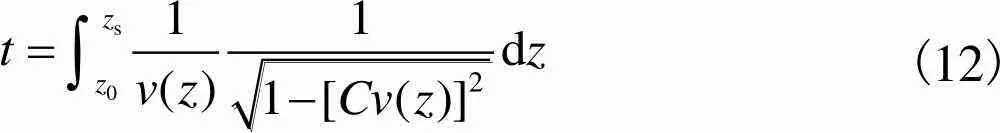
   (12)

   (13)

   (14)

2.3 位置信息融合

经过3条路径估计出的3个坐标用加权平均法进行信息融合，最后得到的坐标即为目标位置．由于信号传输可信度与传输路径长度有关，可用传输时间的长短来判断权值的大小，即

   (15)

则最终目标估计位置坐标表示为

   (16)

2.4 算法复杂度分析

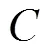
3 定位误差分析

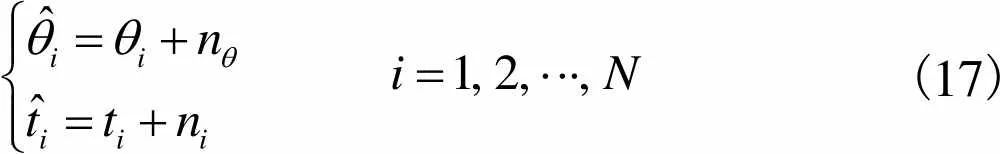
   (17)

似然函数为

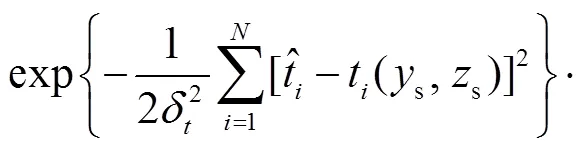
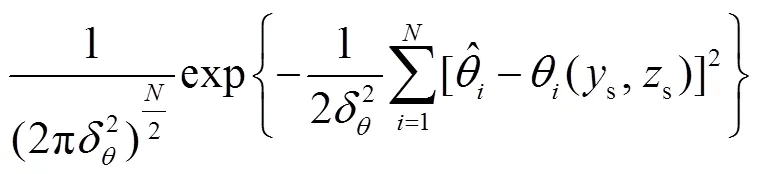
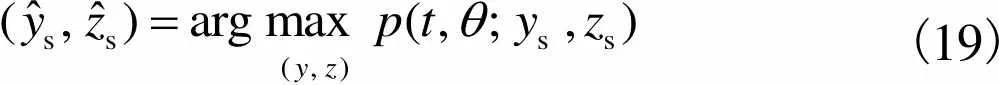
   (19)

     (20)

   (21)

   (22)

   (23)

根据式(11)和式(12)，能得到

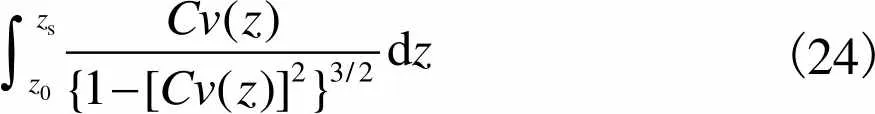
     (24)

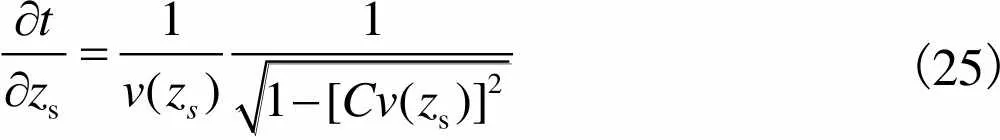
   (25)

   (26)

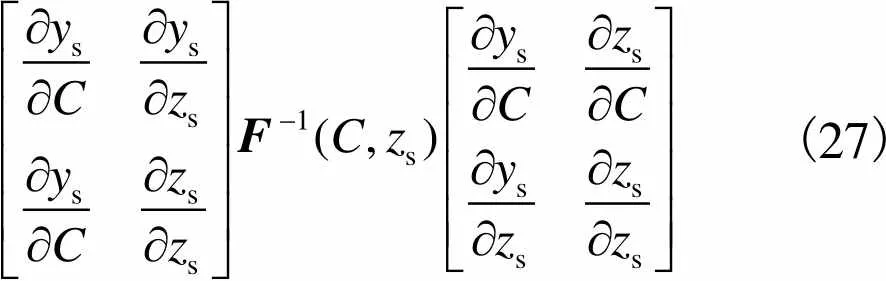
     (27)

式中：

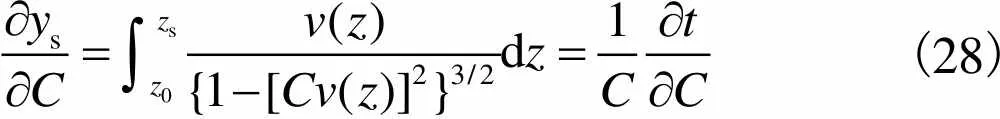
   (28)

   (29)

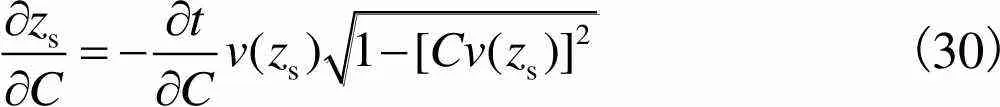
   (30)

对目标位置估计的均方根误差(root mean square error，RMSE)定义为

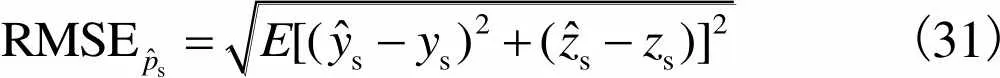
   (31)

所以其理论下界，即克拉美罗界可以表示为

   (32)

4 仿真实验

4.1 不同噪声下的定位误差对比

图4 不同角度方差下的定位误差

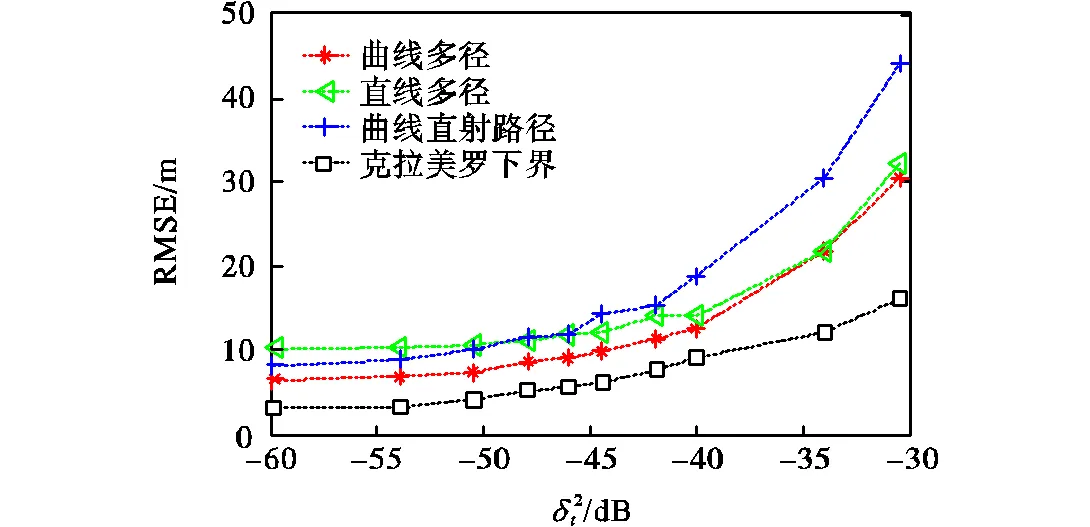
图5 不同时间方差下的定位误差

4.2 不同距离下的定位误差对比

图6 不同距离下定位误差

4.3 累积分布函数与定位误差的关系

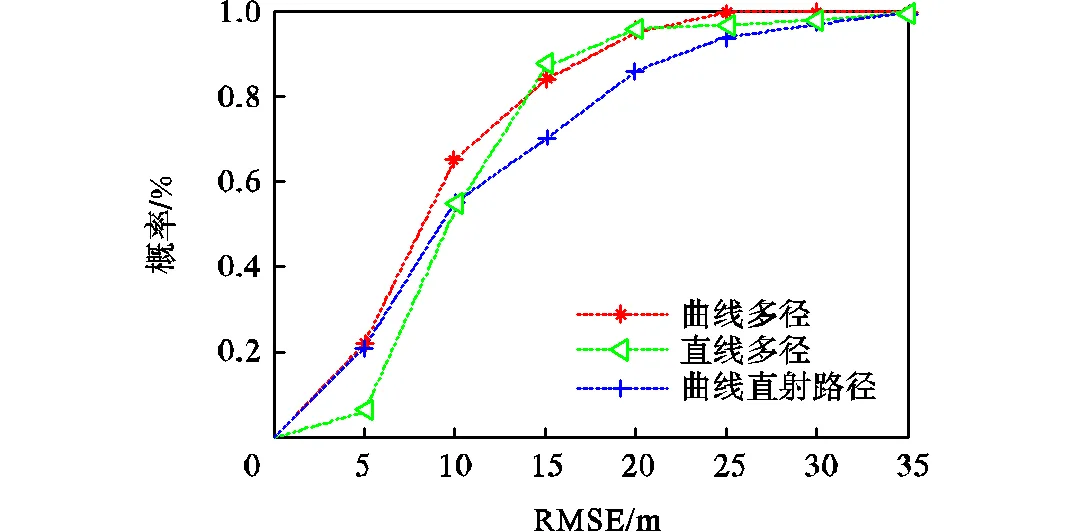
图7 CDF曲线

5 结 语

针对浅海多径环境中海水媒质分布不均匀的特性，本文提出了一种非均匀媒质中联合TOA和DOA的定位算法．该算法只用单独锚节点即可完成定位，并能有效地减少移动的拓扑结构对定位产生的影响．首先对锚节点关于反射面建立虚拟节点，之后获得到达时间和到达角度，并利用费马原理求出不同路径的曲线模型，最后根据测得数据估计目标节点的位置．仿真结果表明，该算法在定位精度中优于传统的直线传输模型，并且具有较好的鲁棒性．

［1］ 黎作鹏，蔡绍滨，张 菁，等. 水声传感器网络节点定位技术综述[J]. 小型微型计算机系统，2012，33(3)：12-17.

Li Zuopeng，Cai Shaobin，Zhang Jing，et al. Survey on node localization technology of underwater acoustic sensor networks[J].，2012，33(3)：12-17(in Chinese).

［2］ Tan H P，Diamant R，Seah W K G，et al. A survey of techniques and challenges in underwater localization[J].，2011，38(14/15)：1663-1676.

［3］ Akyildiz I F，Pompili D，Melodia T. Underwater acoustic sensor networks: Research challenges[J].，2005，3(3)：257-279.

［4］ Stojanovic M，Preisig J. Underwater acoustic communication channels：Propagation models and statistical characterization[J].，2009，47(1)：84-89.

［5］ Cheng W，Teymorian A Y，Ma L，et al. Underwater localization in sparse 3D acoustic sensor networks [C]//27. Arizona，USA，2008：236-240.

［6］ Yuan Y X，Carter C，Salt J E. Near-optimal range and depth estimation using a vertical array in a correlated multipath environment[J].，2000，48(2)：317-330.

［7］ Abdi A，Guo H. Signal correlation modeling in acoustic vector sensor arrays[J].，2009，57(3)：892-903.

［8］ Emokpae L E，Dibenedetto S，Potteiger B，et al. UREAL：Underwater reflection-enabled acoustic-based localization[J].，2014，14(11)：3915-3925.

［9］ Han G，Zhang C，Shu L，et al. Impacts of deployment strategies on localization performance in underwater acoustic sensor networks[J].，2015，62(3)：1725-1733.

［10］ Berger C R，Zhou S，Willett P，et al. Stratification effect compensation for improved underwater acoustic ranging[J].，2008，56(8)：3779-3783.

［11］ Liu J，Wang Z，Cui J H，et al. A joint time synchronization and localization design for mobile underwater sensor networks[J].，2016，15(3)：530-543.

［12］ Ameer P M，Jacob L. Localization using ray tracing for underwater acoustic sensor networks[J].，2010，14(10)：930-932.

［13］ Ramezani H，Jamali-Rad H，Leus G. Target localization and tracking for an isogradient sound speed profile [J].，2013，61(6)：1434-1446.

［14］ Ramezani H，Leus G. Accurate ranging in a stratified underwater medium with multiple isogradient sound speed profile layers[J].，2012，45(5)：146-151.

［15］ Casalino G，Turetta A，Simetti E，et al. RT 2：A real-time ray-tracing method for acoustic distance evaluations among cooperating AUVs[C]//. Sydney，Austra-lia，2010：1-8.

［16］ Poursheikhali S，Zamiri-Jafarian H. Ranging in underwater wireless sensor network：Received signal strength approach[C]//. Doha，Qatar，2016：1-6.

［17］ Zhang B，Wang H，Xu T，et al. Received signal strength-based underwater acoustic localization considering stratification effect [C]//. Shanghai，China. 2016：1-8.

［18］ Yu J，Zhang L，Liu K. Coherently distributed wideband LFM source localization[J].，2015，22(4)：504-508.

［19］ 王永良，陈 辉，彭应宁，等. 空间谱估计理论与算法[M]. 北京：清华大学出版社，2004.

Wang Yongliang，Chen Hui，Peng Yingning，et al.[M]. Beijing：Tsinghua University Press，2004(in Chinese).

［20］ Kim E，Lee S，Kim C，et al. Floating beacon-assisted 3-D localization for variable sound speed in underwater sensor networks[C]//. Basel，Switzerland，2010：682-685.

(责任编辑：王晓燕)

Joint TOA and DOA Localization Algorithm in Shallow Ocean Multipath Environment

Liu Kaihua1，Wei Chongchong1，Yu Jiexiao2

(1．School of Microelectronics，Tianjin University，Tianjin 300072，China；2．School ofElectrical and Information Engineering，Tianjin University，Tianjin 300072，China)

To overcome the problem caused by the inhomogeneous water medium，a joint time-of-arrival(TOA) and direction-of-arrival (DOA) localization algorithm considering the inhomogeneous water medium in shallow ocean multipath environment is proposed. This algorithm can not only avoid the slanted path induced by the various sound speeds，but also reduce the influence of dynamic underwater network topology. Firstly，the virtual node (VN) of the anchor node was set up based on the surface and the bottom of the sea to convert the non-line-of-sight (NLOS) problem into a line-of-sight (LOS) problem. Then，according to the known sound speed profile (SSP)，the numerical path of signal was derived by using Fermat’s principle. Furthermore，due to the irregularity of sea surface and seabed，the signal was scattered at the reflection point. So the reflection point was regarded as a distributed source，and the central angle and the average arrival time was regarded as DOA and TOA，respectively. Finally，the location parameter of target was estimated by TOA and DOA. The simulation results indicate that the proposed method is superior to conventional straight line propagation model in location accuracy and robustness.

inhomogeneous medium；multipath；sound speed profile；Fermat’s principle；virtual node

10.11784/tdxbz201703045

TP391.9

A

0493-2137(2018)02-0129-06

2017-03-19；

2017-07-07.

刘开华（1956—  ），男，博士，教授，liukaihua@tju.edu.cn.

于洁潇，yjx@tju.edu.cn.

国家自然科学基金资助项目(61501322).

the National Natural Science Foundation of China(No.,61501322).