多档位行星变速传动系统动力学参数优化修改
2018-03-05窦作成李以农杜明刚赵腊月
窦作成, 李以农, 杜明刚, 杨 阳, 赵腊月
(1. 重庆大学 机械传动国家重点实验室,重庆 400044; 2. 中国北方车辆研究所,北京 100072)
行星变速传动系统因结构紧凑、容易实现多个档位的传动速比,在车辆传动系统中被广泛采用。近年来行星变速传动系统档位数逐渐增加(6档甚至更多),在增强其传动平顺性等优点的同时也使得系统结构越来越复杂[1],在设计中很容易出现参数选取不合理导致系统多个档位在外界激励下都会发生扭转共振。为避免这种恶劣情况的发生,需要对参数进行动力学优化修改[3-4]。由于行星变速传动系统中不同参数对同一档位固有频率有不同的影响,而同一参数对不同档位的固有频率影响也存在差别。因此,仅依靠人工对参数进行修改来获得满足行星传动变速系统所有档位固有频率都避开工作转速的要求需要耗费大量的人力和时间,而且很难得到一个最优的调节效果。那么建立一种高效的针对多档位行星变速传动系统的参数优化修改方法,以获得系统所有档位在工作转速范围内都不出现扭转共振的设计参数具有重要意义。
为避免传动系统出现共振的参数优化修改首先需要进行灵敏度分析,以使参数修改更具针对性。国内外很多学者都进行了行星传动系统固有频率对参数灵敏度的研究, Guo和Lin等[2-5]研究了行星齿轮啮合刚度、转动惯量对行星排固有特性和振动模态应变能的影响。齐寅明等[6]分析了由三级简单行星排构成的盾构机减速器固有特性及对参数灵敏度。黄毅、刘辉等[7-8]针对车辆传动系统动力学响应进行了灵敏度分析。在计算出传动系统固有频率对系统参数的灵敏度后,需要通过动力学参数修改才能达到避免系统出现共振、减小系统振动的目的。项昌乐等[9]采用多步灵敏度法对车辆传动系统某一档参数进行了动力学修改,得到了某个参数调整后系统固有频率的变化情况。张代胜等[10]通过建立扭转刚度和转动惯量对固有频率的影响曲线来寻找较优的参数,以达到减小传动系统振动的目的。现有的文献只对变速传动系统一个档位或定传动比系统出现共振时进行系统参数优化修改,还没有针对多个档位同时出现扭转共振的行星变速传动系统进行动力学参数优化修改的研究。
本文建立了多档位行星变速传动系统集中参数模型,分析了系统扭转振动固有频率对齿轮间啮合刚度、轴段扭转刚度和各构件转动惯量的相对灵敏度,并以此作为参数优化约束条件。为获得更好的参数优化结果,采用基于遗传算法的多步优化方法,每步优化中均采取相对初始参数变化率最小的动态优化目标和动态约束条件。对比分析了该优化方法和单步独立最优得到的优化结果,并研究了优化步长对优化结果的影响。对行星传动系统固有频率对参数灵敏度用于传动系统多个档位和单个档位参数优化修改的特点进行了分析。并分析了系统参数不确定性引起的共振档位固有频率稳定性。
1 系统动力学模型
根据某多级行星变速传动系统结构,建立图1所示扭转振动集中参数模型。该系统共有三个行星排,行星排1、行星排2为含有4个行星轮的简单行星排,行星排3为含有两类各3个行星轮的复合行星排。各行星排中行星轮均沿圆周等距分布,相同类型的行星轮质量、转动惯量以及轮齿啮合刚度取相同值。Ci(i=1,2,3,L,H,R)为行星变速传动系统中离合器,通过改变各离合器结合分离组合方式,该行星变速传动系统可以实现8个档位的传动。系统包含29个构件,但是由于每个档位都有两个离合器结合,因此系统每个档位含有27个旋转方向自由度。Ji(i=1,2,3,H1,H2)为各惯性元件转动惯量:其中,J1为发动机至变速传动系统动力输入端传动构件等效到动力输入端的等效转动惯量;J2、J3为动力输出端至车轮各传动构件转动惯量和车体平动质量的等效惯量转换到动力输出端的等效转动惯量。ki(i=1~8)为各惯性元件间连接件扭转刚度。
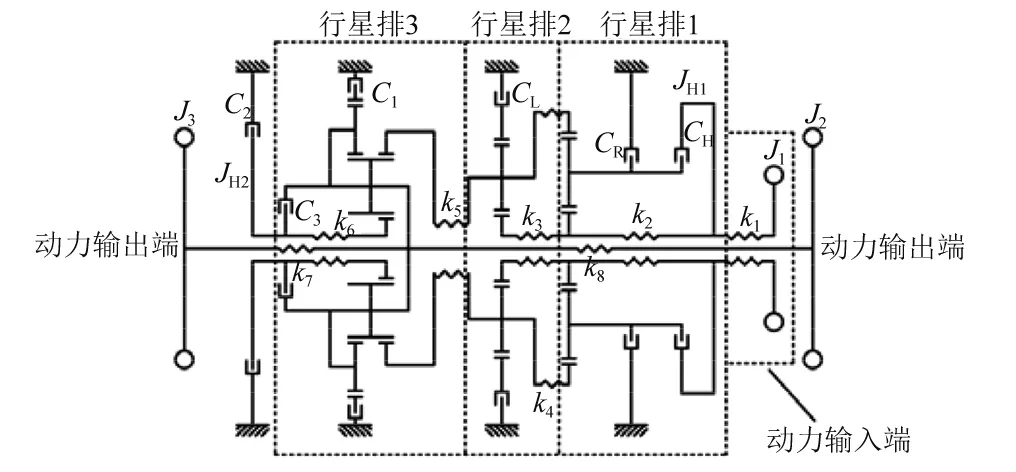
图1 多档位行星变速传动系统扭转振动模型Fig.1 Torsional vibration model of multi-speed planetary transmission
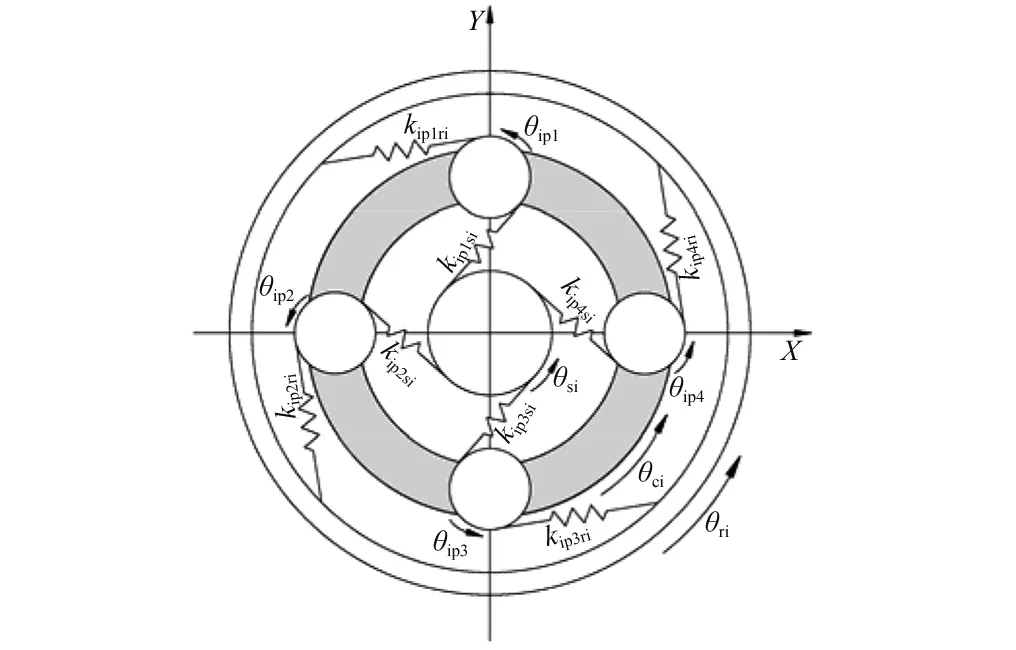
图2 简单行星排1、2集中参数模型Fig.2 Lumped parameter model of simple planetary set 1 and 2
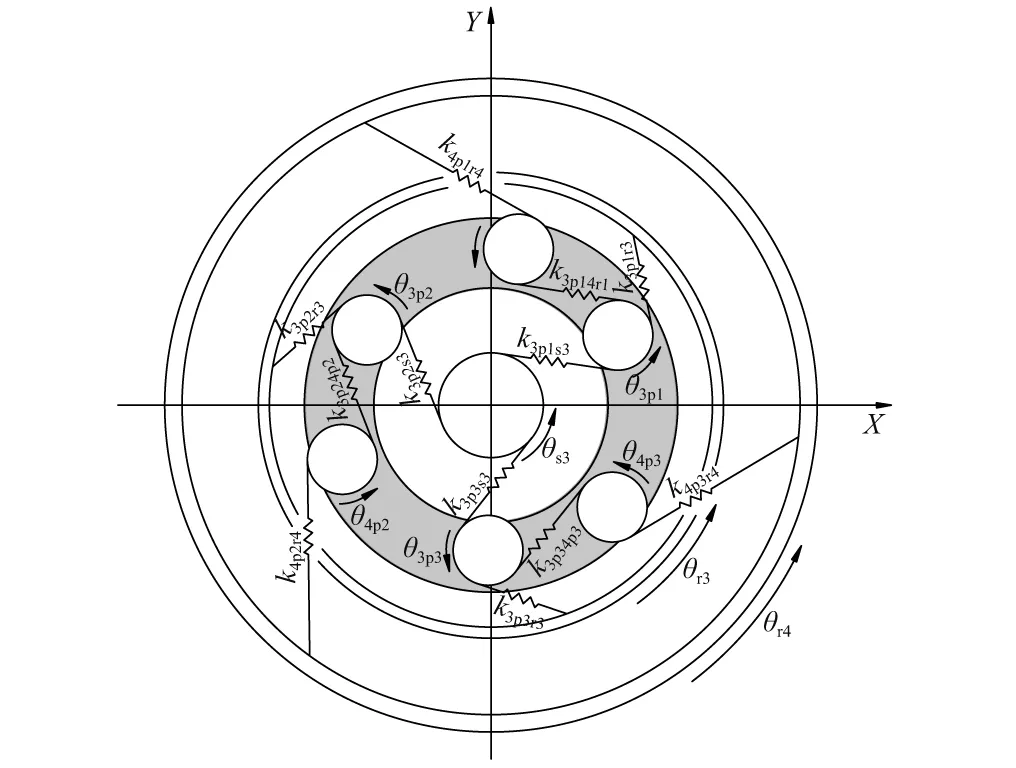
图3 复合行星排3集中参数模型Fig.3 Lumped parameter model of compound planetary set 3
行星变速传动系统中行星排坐标系设定为:太阳轮、行星架和齿圈取绝对坐标系,行星轮的坐标系取为随行星架同步旋转的转动坐标系。分析中设定所有构件沿逆时针旋转方向为正方向,轮齿的相互压缩方向为变形的正方向,图2、图3给出了简单行星排1、2和复合行星排3各构件的正向旋转方向及相互啮合关系。图2中,kipjsi为简单行星排i中第j个行星轮与其太阳轮si间的啮合刚度,kipjri为简单行星排i中第j个行星轮与其齿圈ri间的轮齿啮合刚度,(i=1,2;j=1,2,3,4);图3中,k3pjsi为复合行星排3第j个内圈行星轮与其太阳轮s3间的啮合刚度,k3pjri为复合行星轮3第j个内圈行星轮与其齿圈r3间的啮合刚度,k4pjri为复合行星排3第j个外圈行星轮与其齿圈r4间的啮合刚度,k3pj4pj为复合行星排3第j个内圈行星轮与第j个外圈行星轮间的啮合刚度,(j=1,2,3)。
运用拉格朗日方程建立系统扭转振动微分方程,方程中含有27个旋转方向自由度,由于各档位离合器的结合方式不同使得不同档位下的运动构件不同,每一档位的运动微分方程需要单独列写。为了文章精简此处仅给出通用方程式。
L=T-U
(1)
(2)
式中:T为行星变速传动系统动能;U为行星变速传动系统扭转弹性势能;L为拉格朗日泛函。
由拉格朗日方程得到系统矩阵形式的无阻尼扭转振动微分方程:
(3)
根据系统各构件自由振动响应函数q=θiejwit,由式(3)得到计算系统固有频率和振型的特征方程
(4)
式中:ωi为系统第i阶固有频率,Θi为系统第i阶固有频率对应振型,J为系统惯性矩阵,K为系统刚度矩阵。
根据式(4)可以计算得到行星变速传动系统各档位的固有频率。表1为行星变速传动系统参数,其中齿轮平均啮合刚度值通过文献[11]计算得出;当离合器将两个构件结合时,其转动惯量进行相加处理。表2为行星变速传动系统8个档位固有频率,由式(22)可知系统的工作转速范围为26.67~81.67 Hz,因此只需对系统前5阶固有频率进行分析研究即可。

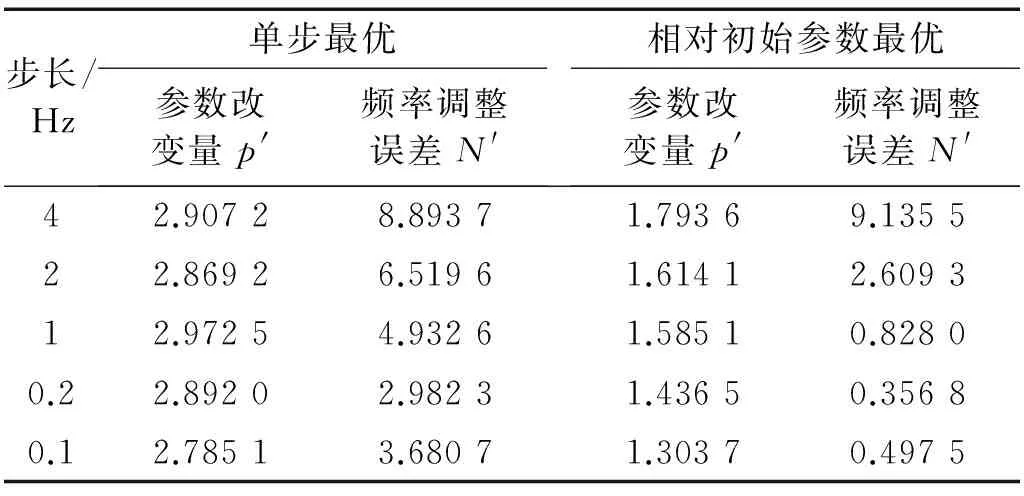
表1 行星变速传动系统参数
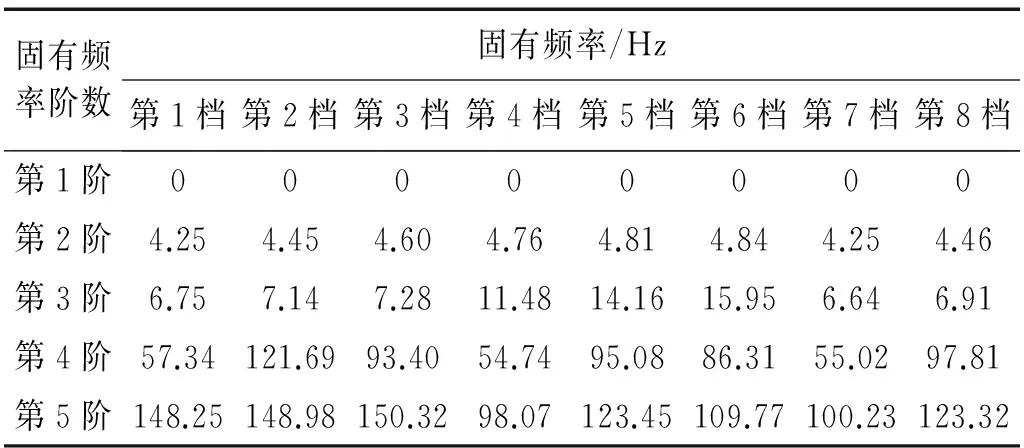
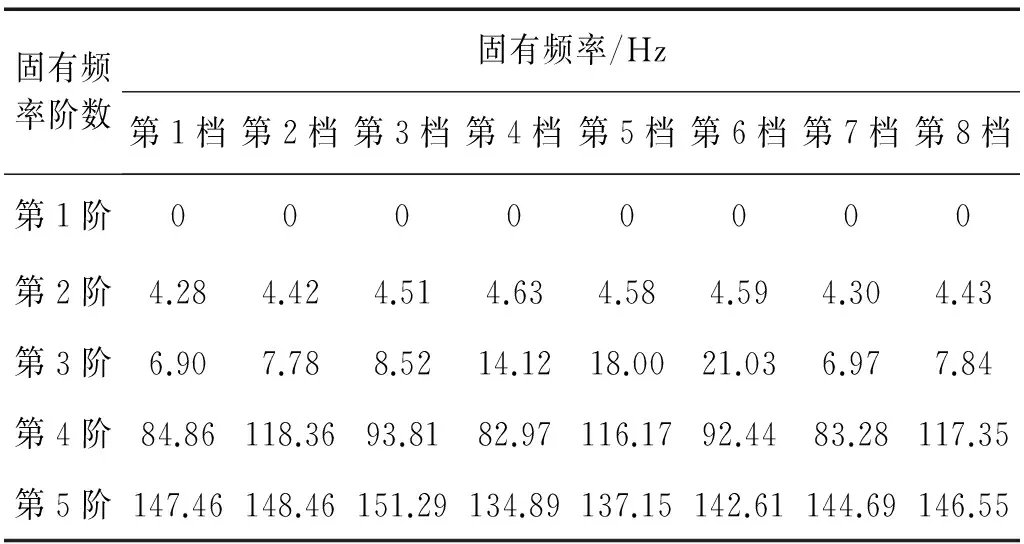
表2 行星变速传动系统各档位前5阶固有频率
2 固有频率对参数相对灵敏度
在计算传动系统固有特性对参数灵敏度时通常是采用式(4)直接对参数求偏导,以获得参数改变一绝对数值后固有特性改变量[12-13],称为绝对灵敏度。这种方式得到的灵敏度值不能直接进行不同参数间灵敏度大小的比较,当参数间存在数量级差别时,利用灵敏度进行动力学修改时需要进行无量纲化处理以减小计算误差[14]。为此,本文用式(4)对参数的变化率求偏导来避免前面两个问题,称为相对灵敏度。为了简便,后面提到的灵敏度都是指相对灵敏度。
由式(4)对参数变化率xm求导,得

(5)
(6)
根据特征方程中无重根部分矩阵正交条件:
(7)
由式(6)、式(7)可得系统固有频率对构件参数变化率灵敏度计算公式
(8)
系统参数变化率为xm=Δx/x,x为系统参数值,那么式(8)最终可化为
(9)
由式(9)可以得到固有频率对转动惯量变化率的灵敏度
(10)
固有频率对刚度变化率的灵敏度
(11)
3 基于遗传算法的多档位参数优化修改模型
通过固有频率对参数的灵敏度计算可以知道各参数对每一阶固有频率影响的大小,但是当多个参数都对固有频率有影响时就很难获得一个最优的调整结果,因此需要采取优化算法来帮助获得一个最优解。遗传算法根据适者生存、优胜劣汰等自然进化规则搜索和计算问题的解,相比于线性规划等传统优化算法,遗传算法不容易陷入局部最优,可以更好地获得最优解。
当知道固有频率的调整量,以及通过式(10)、式(11)获得固有频率对各参数的灵敏度后可以确定遗传优化算法的等式约束条件[15]:
[S]{Δp}={ΔN}
(12)
式中:ΔN为系统需要调整的n个固有频率调整向量, {ΔN}=[ΔN1,ΔN2,ΔN3,…,ΔNn]T;Δp为q个需要调整的参数调整率向量, {Δp}=[Δp1,Δp2,Δp3,…,Δpq]T; [S]为需要调整的n个固有频率对需要调整的q个参数的灵敏度, 为n×q阶Jacobi矩阵
(13)
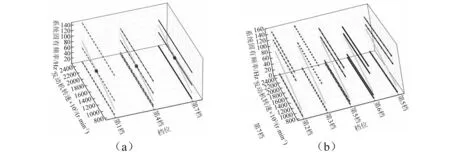
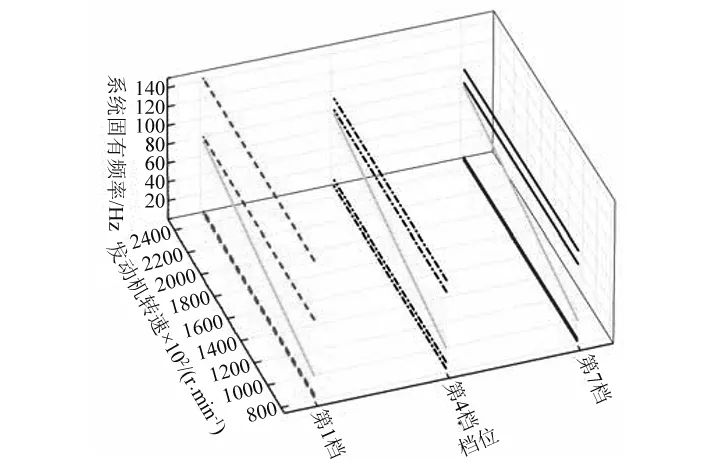
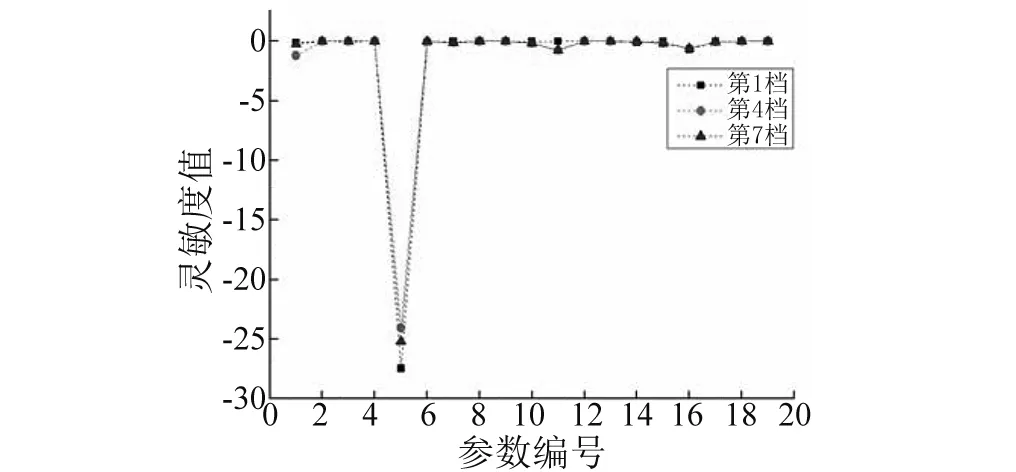
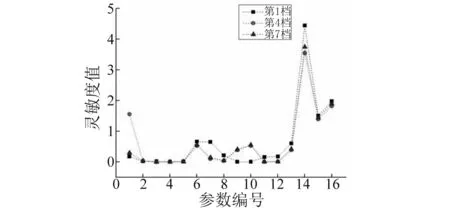
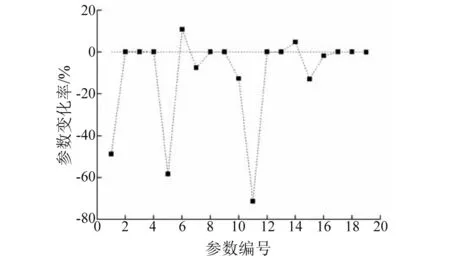
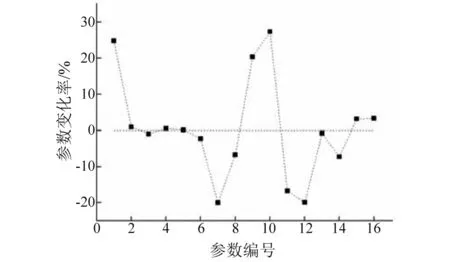
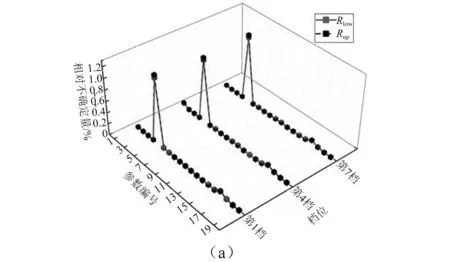
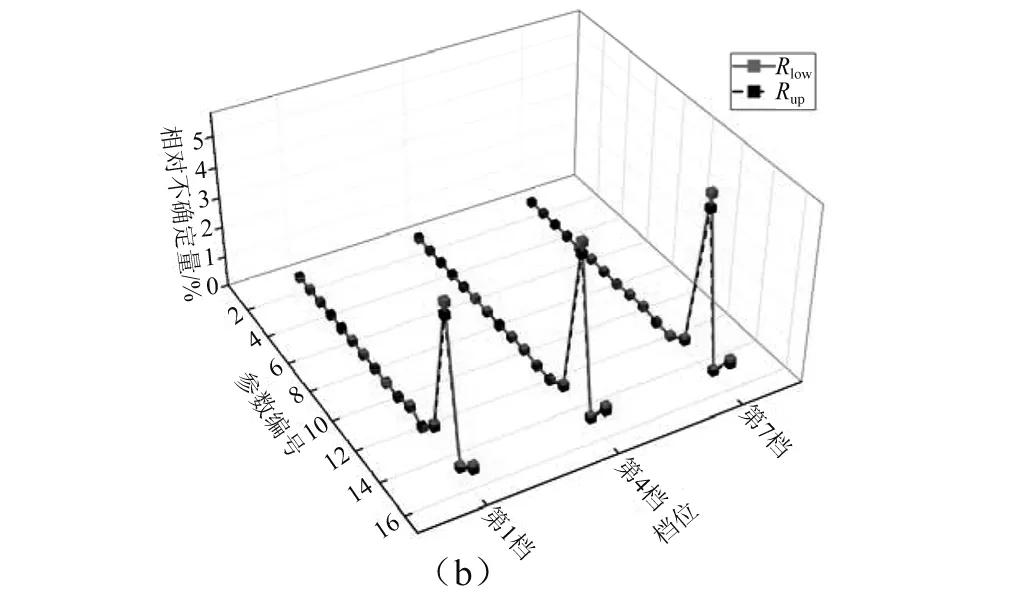
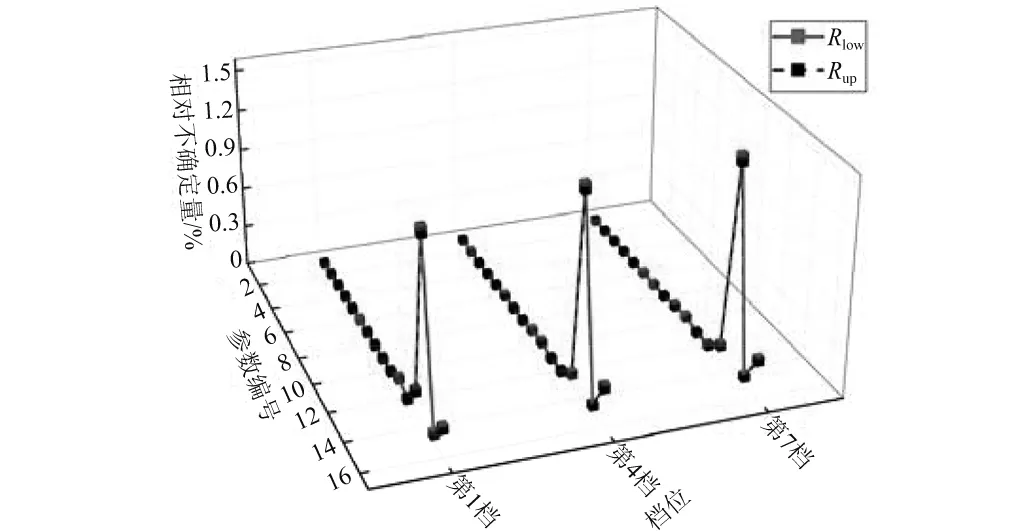
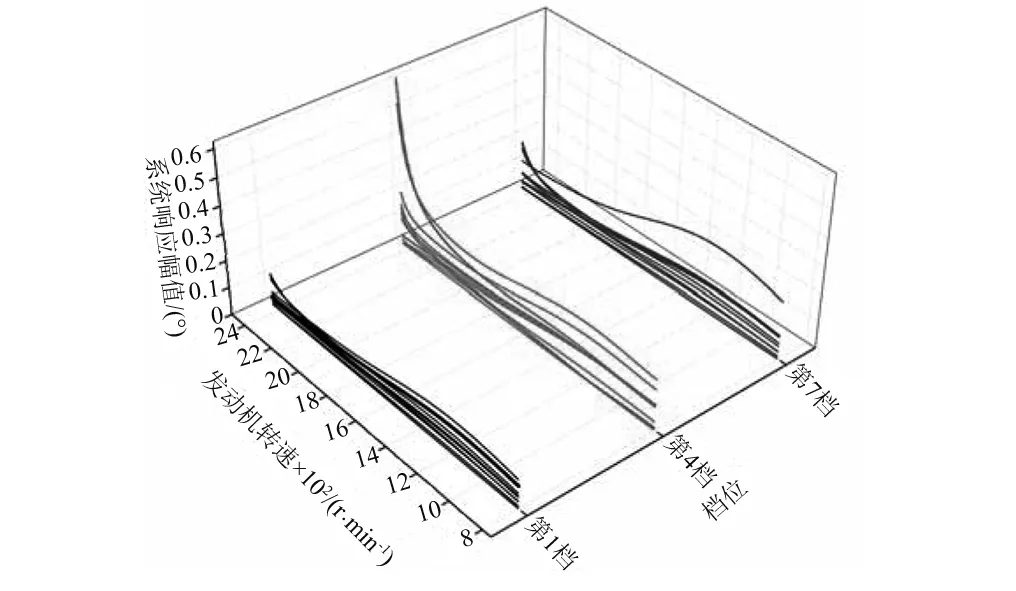
一般实际应用中,需要调整的固有频率数少于需要调整的参数数目,即n minf(Δp)={Δp}T{Δp} (14) (15) 式中:Ulow、Uhigh分别为参数调整的下界和上界。 调整后的参数为: (16) 式(14)~(16)的参数优化调整方法只能运用于小幅度的调整,当需要调整的固有频率和参数较大时需要采取多步调整。如果直接采用式(14)作为优化函数,Δp为相对前一步调整得到的参数改变率,最后调整完成后得到的相对最初参数调整率平方和不一定最小。为了使相对初始参数调整率平方和最小,第i步参数调整的目标优化函数变为式(17)所示 (17) 式中:Pi-1为第i-1步调整后得到的参数向量;P0为系统初始参数向量;Δpi为第i步优化调整得到的参数相对第i-1步调整后得到的参数改变率向量。 那么约束方程中第i步调整时参数的最大改变率应该变为式(18)所示 (18) 将式(18)进行移项化简处理后有 (19) 综合式(14)~(19)得到优化算法的每一步优化调整的最优函数和约束条件为 (20) 优化调整后得到系统的最终参数为 (21) 该行星变速传动系统由V型8缸柴油发动机驱动,工作转速为800 ~2 450 r/min,其输出扭矩的主谐次激励为2谐次(第4谐次)。通过发动机固有频率和转速间转化式(22)可以得出系统固有频率位于26.67~81.67 Hz范围内时将会有扭转共振发生。 (22) 式中:N为系统固有频率(Hz);v为谐次;n为发动机转速(r/min)。 再根据表2中计算得到的系统各档位固有频率,可以知道发动机主谐次激励与各档位固有频率关系如图4所示,第1、4、7档的第4阶固有频率(横线)与发动机工作转速激励(斜线)存在交点(如图4(a)所示),在系统工作中会产生共振,而其它档位不会产生共振(如图4(b)所示)。为了使系统所用档位在发动机工作转速范围内都不会发生共振,需要调整参数使第1、4、7档第4阶固有频率增大使其固有频率分布如图5所示,同时其余各档的固有频率分布保持图4(b)所示的关系。 针对存在共振的第1、4、7档第4阶固有频率,根据式(10),(11)计算得到行星变速传动系统扭转振动固有频率对转动惯量参数的灵敏度(图6)和对刚度参数的灵敏度(图7)。从图6可以看出,转动惯量5(JH2)对第1、4、7档固有频率都有很大的影响,转动惯量1(J1)只对第4档固有频率有较大影响,转动惯量11(Jr2)对第4、7档固有频率有较大影响而对第1档固有频率几乎没有影响,转动惯量参数16(Js3)对三个档位固有频率都有较大影响且大小相近。从图7可以看出,系统固有频率对不同刚度参数的灵敏度值差别较对不同转动惯量参数的灵敏度更小,但不同档位间的固有频率对刚度参数的灵敏度差别较大。第4档固有频率对刚度参数1(k1)的灵敏度明显大于其它两个档位,第4、7档固有频率对除刚度参数1(k1)外的灵敏度值区别较小,而第1档与其它两档有较大的区别。系统同一构件的刚度和转动惯量是存在相互影响的,但是在实际设计中可以通过改变构件的结构分别获得满足要求的刚度值和转动惯量值,因此在研究中认为这两个参数是相互独立的。 图4 系统各档位固有频率-发动机激励关系Fig.4 The relation of natural frequencies of system and engine excitation 图5 系统期望固有频率-发动机激励关系Fig.5 The relation of natural frequencies of system and engine excitation of expectation 图6 系统固有频率对转动惯量灵敏度Fig.6 The sensitivity of natural frequencies to rotational inertias 图7 系统固有频率对刚度灵敏度Fig.7 The sensitivity of natural frequencies to stiffnesses 由式(22)得到的发动机主谐次扭转振动激励在工作转速范围内对应的最高频率为81.67 Hz,那么可设定调整的目标固有频率大于等于82 Hz。系统三个需要调整档位取相同的调整量,再根据表2中三个档位的第4阶固有频率设定固有频率目标调整量ΔN=28 Hz。由于固有频率调整量较大,需采用多步参数优化以获得更为精确的调整目标,每步调整量为nHz。表3为设定参数最大可调整范围为±100%,固有频率取不同调整步长时,分别以式(14)为优化函数的单步最优和以式(17)为优化函数的相对初始参数最优进行优化计算,得到的不同优化结果。参数优化修改的结果好坏通过式(23)所示参数调整率平方和p′与式(24)所示三个档位固有频率调整误差的平方和N′来体现,p′和N′的值越小说明优化的结果越好。 (23) (24) 表3 取不同调整步长得到的参数改变量和频率调整误差 图8 系统优化前后转动惯量变化率Fig.8 The change ratio of the rotational inertia after optimization 图9 系统优化前后刚度变化率Fig.9 The change ratio of the stiffness after optimization 从表3可以看出,不管是采用单步最优还是采用相对初始参数最优,固有频率误差都随步长减小而逐渐减小。但是当步长取0.1时两种优化方式得到的固有频率误差都比步长取0.2时更大,这是由于步长取得过小后计算的累积误差开始大于精度提高后获得的灵敏度误差减小量。采取单步最优时步长对参数改变量影响较小,p′大约都为2.9左右。而采取相对初始参数最优时,参数改变量随步长减小而逐渐减小,同时在任意步长下采取相对初始参数最优得到的参数改变量都远小于采取单步最优获得的参数改变量,同时固有频率调整误差也更小,说明采用相对初始参数最优可以获得相比采用单步最优更好的参数优化修改结果。 根据表3中的结果,以固有频率调整步长取0.2 Hz时得到的参数优化修改结果作为最终优化修改参数。图8、9分别为行星变速传动系统参数优化修改后转动惯量参数和刚度参数变化率。 从图8中可以看出转动惯量1(J1)、5(JH2)、11(Jr2)的变化率比较大,其中转动惯量11(Jr2)减小了近70%,转动惯量1(J1)和转动惯量5(JH2)分别减小了约50%和60%。从图9中可以看出,刚度7(k7)、12(k2pjs2)减小了20%,刚度11(k2pjr2)减小了17%,刚度1(k1)、10(k1pjs1)增大了约25%,刚度9(k1pjr1)增大了20%。总体来说刚度参数相对于转动惯量参数来说调整幅度更小,同时刚度参数调整更加均匀。对比图8和图9,除刚度9(k1pjr1)和转动惯量7(Jr1)的变化涉及到同一构件r1外,其它各参数都只受到不同的构件影响,即参数的调整不会出现相互矛盾的情况。可以直接通过改变构件厚度或增轮缘厚度和辐板厚度的方式来改变构件的转动惯量和齿轮啮合刚度,通过改变轴段半径的方式来轴段刚度,这样可以不用改变传动系统的结构和传动比,以实现较小的改变即可达到参数修改的目的。刚度9(k1pjr1)和转动惯量7(Jr1)调整量都不大,减小行星齿轮和齿圈的轮缘厚度的同时增大其辐板厚度,或将齿圈用质量更轻强度更高的材料代替可获得同时满足调整要求的参数值。 从图6、7中系统扭振固有频率对转动惯量和刚度的灵敏度计算结果以及相关文献[4,6]的研究都可以得出:行星传动系统扭振固有频率对转动惯量的灵敏度都≤0,对刚度的灵敏度都≥0,即要使系统固有频率增大需要减小构件的转动惯量或者增大构件刚度。当对某一确定系统或行星变速传动系统某一个档位进行动力学修改时可以根据这一原则进行参数调节。但从系统优化前后参数变化率(图8、9)可以看出,当设定所有档位的调整目标都是增大其固有频率时,却出现某些构件的转动惯量增大以及刚度减小的情况。因为仅根据灵敏度正负值进行参数调节时可能会出现其中某一档固有频率满足目标调整量而另外某档固有频率调节量过大,为了使所有档位同时满足目标调整量就需要对参数进行反向调节。因此对多档位行星传动系统进行基于固有频率对参数灵敏计算的动力学参数修改时,仅依靠计算得到的固有频率对各类参数灵敏度值(或者固有频率随参数改变的变化规律)就很难得到满足要求的参数值。 表4 行星变速器优化后各档位前5阶固有频率 表4为行星变速器优化后各档位前5阶固有频率,由表4可以看出,对参数进行动力学优化修改后的行星变速传动系统各档位固有频率都不再位于发动机工作转速范围内,即所有档位固有频率都小于26.67 Hz或大于81.67 Hz。对比表2中参数优化修改前行星变速传动系统各档位固有频率,系统8个档位的前3阶固有频率变化都不大,这保证了系统不会在发动机低转速激励下出现扭转共振。除第1、4、7档的第4阶固有频率有较大幅度的增大外,第5、8档有20 Hz左右的增大,但这种增大是设计中所期望的,其它档位仅有微小的变化。 图10 固有频率相对不确定量(5%)Fig.10 Relativity uncertainty of natural frequencies(5%) 因系统构件制造、装配误差等会引起参数不确定导致固有频率变化。从表4可以看出,系统参数优化后第1、4、7档第4阶固有频率离系统最高工作转速81.67 Hz较近,因此需要对这三个档位第4阶固有频率因参数波动引起的固有频率稳定性问题进行研究。为避免因固有频率波动致使系统再次出现共振的最大允许波动量为1.5%。根据文献[16]中求解区间特征值问题的非迭代方法求得系统一个参数波动范围为5%,而其它参数没有波动时固有频率的相对不确定量,如图10所示。图10(a)、(b)分别为转动惯量和刚度参数波动引起的系统第1、4、7档第4阶固有频率相对不确定量,图中Rlow和Rup分别表示相对不确定量的下界和上界。从图10中可以看出,转动惯量波动引起的固有频率相对不确定量较小,最大值由J5(JH2)引起,仅为1.2%,不会导致系统出现共振;刚度参数引起的固有频率相对不确定量较大,由k14(k3pjs3)引起的相对不确定量已达5%,会导致系统出现共振。当k14(k3pjs3)波动量低于1.5%时可使系统固有频率相对不确定量低于1.5%,以确保不会发生扭转共振,图11为刚度波动1.5%时引起的固有频率相对不确定量。 图11 固有频率相对不确定量(1.5%)Fig.11 Relativity uncertainty of natural frequencies(1.5%) 图12、13分别为行星变速传动系统参数优化前、后发动机主谐次激励下系统第1、4、7档位各构件扭转振动响应幅值随发动机转速的变化图。从图12中可以看出,参数优化前第1、4、7档有明显的共振峰值,其中第4档振动最大值超过了1.5°,第4、7档最大幅值也超过0.5°。比对图13中参数优化后的响应结果,三个档位在发动机工作转速内都没有出现共振峰值,第1档最大扭振幅值小于0.2°,第7档最大扭振幅值为0.25°。扭振幅值最大值出现在第4档的最高转速处,但在实际使用中第4档为中间档位,驱动转速一般不会到达最高,实际工作中参数优化后第4档的扭转振动最大幅值仅为0.2°左右。达到了避免行星变速传动系统各档位在发动机工作转速范围内不发生扭转共振,减小系统扭转振动响应的目的。 图12 参数优化前系统各构件扭转振动响应幅值Fig.12 Torsional response amplitude of elements of the system before optimization 图13 参数优化后系统各构件扭转振动响应幅值Fig.13 Torsional response amplitude of elements of the system after optimization 本文针对行星变速传动系统多个档位同时存在扭转共振的问题,通过共振固有频率对参数的相对灵敏度计算,结合基于遗传算法的多步优化方法对系统参数进行了优化修改,最终使得行星变速传动系统所有档位在工作转速范围内都不出现共振,其主要结论如下: (1) 采用多步参数优化修改方法时,每步都以相对初始参数变化率的平方和最小为优化目标可以获得相比以单步参数变化率的平方和最小为优化目标更好的优化结果,而选取过小的固有频率调整步长反而会使得最终的优化结果变差。 (2) 行星变速传动系统不同档位固有频率对同一参数灵敏度不同,不同档位固有频率对刚度参数的灵敏度较对转动惯量的灵敏度差别更大。 (3) 单个档位固有频率对构件转动惯量灵敏度为负,对轴段扭转刚度和齿轮啮合刚度灵敏度为正,但对多个档位进行参数优化修改时,仅通过某个参数灵敏度值来修改参数的调节方式不再有效。 (4) 根据参数优化目标对多档位行星变速系统参数进行优化修改,优化后系统所有档位在工作转速范围内都不会发生扭转共振,系统构件扭转振动响应幅值明显减小。 [ 1 ] INALPOLAT M, KAHRAMAN A. Dynamic modelling of planetary gears of automatic transmissions [J]. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics, 2008, 222(3): 229-242. [ 2 ] GUO Y, PARKER R G. Sensitivity of general compound planetary gear natural frequencies and vibration modes to model parameters [J]. Journal of Vibration and Acoustics, 2010, 132(1): 011006. [ 3 ] 刘辉, 项昌乐, 郑慕侨. 车辆动力传动系固有特性灵敏度分析及动力学修改[J]. 汽车工程, 2003, 25(6): 591-594. LIU Hui, XIANG Changle, ZHENG Muqiao. Sensitivity analysis and dynamic modification of natural characteristic in vehicle powertrain [J]. Automotive Engineering, 2003, 25(6): 591-594. [ 4 ] XIANG C L, HUANG Y, LIU H. Response sensitivity and the assessment of nonlinear vibration using a nonlinear lateral-torsional coupling model of vehicle transmission system [J]. Journal of Vibration & Acoustics, 2015, 137(3): 031013-11. [ 5 ] LIN J, PARKER R G. Sensitivity of planetary gear natural frequencies and vibration modes to model parameters [J]. Journal of Sound and Vibration, 1999, 228(1): 109-128. [ 6 ] 齐寅明, 龚宪生, 张干清, 等. 盾构刀盘驱动三级行星齿轮系统固有特性及灵敏度分析[J]. 振动与冲击, 2013, 32(15): 14-19. QI Yinming, GONG Xiansheng, ZHANG Ganqing, et al. Natural characteristics and sensitivity analysis of a 3-stageplanetary gears train used in shield machine cutter driver[J]. Journal of Vibration and Shock, 2013, 32(15): 14-19. [ 7 ] 黄毅, 刘辉, 项昌乐, 等. 车辆传动系统非线性平移扭转耦合振动响应灵敏度研究[J]. 振动与冲击, 2014, 33(23): 92-99. HUANG Yi, LIU Hui, XIANG Changle, et al. Response sensitivity of nonlinear translation-torsional vibration coupled model of a vehicle transmission system [J]. Journal of Vibration and Shock, 2014, 33(23): 92-99. [ 8 ] 刘辉, 蔡仲昌, 曹华夏, 等. 车辆动力传动系统扭转强迫振动响应灵敏度研究[J]. 兵工学报, 2011, 32(8): 939-944. LIU Hui, CAI Zhongchang, CAO Huaxia, et al. Sensitivity analysis of forced torsional vibration on vehicle powertrain [J]. Acta Armamentarii, 2011, 32(8): 939-944. [ 9 ] 项昌乐, 廉晓辉, 周连景. 针对实际传动系统的灵敏度分析与动力学修改[J]. 中国机械工程, 2006, 17(3): 325-328. XIANG Changle, LIAN Xiaohui, ZHOU Lianjing. Sensitivity analysis and dynamic modification based on the physics model of vehicular powertrain [J]. China Mechanical Engineering, 2006, 17(3): 325-328. [10] 张代胜, 王浩. 基于灵敏度分析的汽车动力传动系扭振特性优化 [J]. 中国机械工程, 2013, 24(5): 685-689. ZHANG Daisheng, WANG Hao. Optimization of vehicle drivetrain torsional vibration characteristics based on sensitivity analysis [J]. China Mechanical Engineering, 2013, 24(5): 685-689. [11] 渐开线圆柱齿轮承载能力计算方法:GB/T 3480—1997 [S]. 北京:国家技术监督局, 1997. [12] QU Z Q. Hybrid expansion method for frequency responses and their sensitivities, Part I: undamped systems [J]. Journal of Sound and Vibration, 2000, 231(1): 175-193. [13] QU Z Q, SELVAM R. Hybrid expansion method for frequency responses and their sensitivities, Part II: viscously damped systems [J]. Journal of Sound and Vibration, 2000, 238(3): 369-388. [14] 王东华, 刘占生, 窦唯. 基于混合遗传算法的转子系统优化设计[J]. 振动与冲击, 2009, 28(5): 87-91. WANG Donghua, LIU Zhansheng, DOU Wei. Rotor dynamics optimization based on a hybrid genetic algorithm[J]. Journal of Vibration and Shock, 2009, 28(5): 87-91. [15] 钟一谔,何衍宗,王正,等. 转子动力学[M]. 北京:清华大学出版社,1987: 95-97. [16] CHEN S, QIU Z, SONG D. A new method for computing the upper and lower bounds on frequecies of structures with interval parameters[J]. Mechanics Research Communications, 1995, 21(6): 583-592.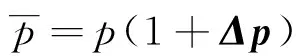
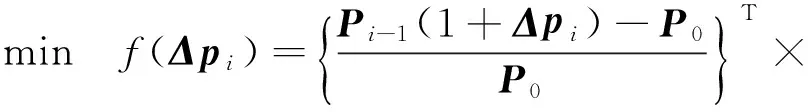
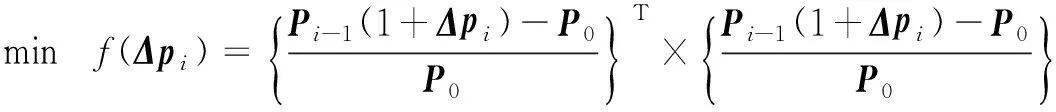
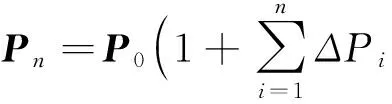
4 优化仿真分析
4.1 系统固有频率对参数灵敏度计算
4.2 参数优化修改
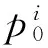

5 结 论
