“微课导学”在课堂教学中的实践与反思*

☉江苏泰州市海陵学校 韩新正

“微课导学”是在现代教学理论引领和信息技术支持下，按照课程标准要求，由教师设计好学生学习的导学稿（任务单），制作好课前学习的“微课”，在课堂上指导学生内化知识、构建知识结构的教学过程.在教学实践中，教师恰当地把微课用在课堂教学中也取得了不错的教学效果.本文拟对“微课导学”在课中的应用做分析，反思课中微课使用的误区，提出解决方案，供参考.

一、课中实践

1.创设情境，引入新课.

好的教学情境能促使学生产生疑问，激发求知欲望，形成强烈的学习动机.传统的教学情境一般都是用PPT来实现，通过图片和文字展示需要创设的情境，如果想制作好的视频，PPT则难以实现，而把视频制作成微课，用于创设情境、引入新课，则能产生良好的效果.比如，设计“勾股定理”起始课的教学情境，如何引入勾股定理，并激起学生的好奇心呢？可以先从一段BBC纪录片《数学的故事》（第1集）中的一段微视频：古埃及人结绳绷成直角三角形（一张截图如图1所示）导入新课.学生在观看时知道埃及人发现了边长为3、4、5的三角形有一个内角是直角，但埃及人没有探索其他的直角三角形三边间的关系，直到两千多年后的希腊数学家毕达哥拉斯才发现毕达哥拉斯定理，并给出证明.这时学生一定会非常好奇，为什么埃及人发现了那些特殊的数，而没有发现一般规律呢？毕达哥拉斯又是怎样发现一般规律的呢？在这样的追问下自然进入勾股定理

的探索过程.

图1

2.辅助讲解，生动有趣.

丰富课堂教学的形式，让学生在“尝鲜”中愉快学习.即使最优秀的教师，学生每天面对同样的风格也会有审美疲劳.偶尔，我们可以选择一些优秀的微课视频给学生观看，一方面满足学生“尝鲜”的好奇心，另一方面，一些讲解深刻、归纳全面、语言优美的名师微课，比教师本人在现场讲解要生动、形象，可以直接借用，能收到良好的教学效果.笔者在讲授“分式概念”起始课时，在抽象出分式的概念、对概念进行辨析之后，如何理解分式？笔者发现有一段微课视频的讲解非常到位，并且主讲人的音质优美，语言流畅，对初步理解分式归纳了四点.所以，现场播放这段3分钟的视频（一张截图如图2所示），然后给学生3分钟时间交流、练习，产生的课堂效果比教师自己讲10分钟的效果还好.另外，笔者在第二轮中考复习讲解中考压轴题时，就直接借用了邵新虎老师的许多微课，邵新虎老师借助几何画板，制作了很多中考压轴题，多数都是精品，可以直接借用.限于篇幅，不详细介绍.理解分式

图2

3.操作演示，直观形象.

课堂教学中，一些操作实验类的问题以学生动手实验、操作为主，以积累活动经验，形成数学直观，但大量的数学实验会占用太多的时间，数学终归是一门思维的科学，它的主要功能是培养人的良好的思维习惯，如何处理两者之间的关系呢？我们认为，在学生动手操作的基础上，对于一些取材困难、实验时间较长的实验，可以观看视频，从别人的实验中感受直观，积累经验.比如，观察正方体被一平面所截的图形，该实验的取材比较困难（有的用白萝卜削成正方体），且观察不同的截面需要很多这样的正方体材料，学生携带不便，课堂实验耗时太长.这时观察视频是个不错的选择，用几何画板制作的动画演示直观形象，不仅能让学生直观看到截面的变化，而且能感受到各种截面之间的过渡关系，这比学生动手操作的效果要好（一张截图如图3所示）.同样，正方体的平面展开图通过观看视频学习的效果也很好.

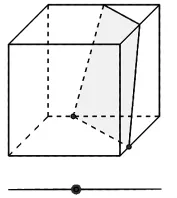
图3

图4

另外，对于一些优美的图案展示，各种精美的几何证明，仅靠教师在课堂上的讲解很难取得良好的效果.借助微课视频可以化抽象为形象，化隐晦为直观.如勾股定理的证明方法多达400多种，教材上一般安排“赵爽弦图”和“邹元治证法”，课上要证完所有的方法是行不通的，但可以把其中的经典证法制作成微视频让学生欣赏，如“美国总统证法”“梅文鼎证法”“欧几里得证法”“毕达哥拉斯证法”等，这样既能保证课堂详略得当，又能让学生尽可能多地了解勾股定理的证法.对于勾股定理文化价值的挖掘，借助微视频能欣赏到各种勾股树（毕达哥拉斯树）的美丽，图4就是利用几何画板的动画效果制作的勾股树的一种.

4.借助微课，互动交流.

翻转课堂最大的好处就是全面提升了课堂的互动性.由于学习的内容安排在课前，课堂上我们就有时间与学生交谈，回答学生的问题，参与到小组的学习，对每个学生进行个别指导.所以，翻转课堂背景下的课堂必须让互动成为主流，师生互动、生生互动成为常态.笔者认为，创新微课视域下的课堂教学，主要就是形成互动的课堂模式.所以，课中使用的微视频就要衔接起课前的微课，一方面通过问题链的形式引领学生合作交流、深入讨论、深度思考、内化知识，另一方面引领学生归纳知识要点，构建知识结构，解决知识运用.

如“分式”第一节课，课前微课呈现的内容主要包括三个方面：分式概念，分式辨析，分式理解.因为受微课时间限制，只能安排这三个内容，但如果学生的学习仅仅就是这三个内容，那么学生首先对为什么要学习分式，分式这一章包含哪些内容，用什么方法来学习分式产生疑问；其次，学习了分式的概念后，对于如何理解分式，没有教师的指点，学生的理解是肤浅的；再次，围绕分式概念构建分式结构，仅靠学生是难以完成的.所以，我们在安排学生课前学习的同时，就要谋划好课内如何解决上述问题，也就是说，要把课前、课中看成一个整体，各有侧重，分别解决不同的问题.课中要解决如下问题：（1）课前学习的分式和小学学习的分数有什么关系？（2）我们学习了分数的概念、分数的基本性质、分数通分、分数约分、分数化简、分数运算等，分式的学习可以按照这一顺序进行吗？大家对照课本看看分式这一章是这样安排的吗？（3）怎样理解分式有无意义？怎样理解分式的值为零？为什么可表示为（5-x）÷（3+x）？提醒大家这为后面的分式运算作了准备.（4）你能画出本章知识的结构图吗？（类比分数，参考本章课时安排）（5）相互交流.

二、反思

翻转课堂中的微课本来是教师为学生课前学习而制作的视频，目的是把学习移到课前，内化知识移到课内，后来在教学实践中，广大教师在课堂上巧妙使用微课，也取得了不错的教学效果，但也出现了一些错误的做法，应引起重视.

1.使用微课必须适时、适当.

课堂上，适当使用微课会取得良好的效果，但一味滥用微课，则适得其反.有种现象值得警惕，教师在课堂上不讲解知识，而是通过播放视频让学生自学.我们知道教学不仅要讲授知识点，更要讲知识结构；不仅要讲数学思想，更要培养学生的情感态度价值观，教师在教学现场，除了传道受业，还有情感交流.显然，这样的做法是把微课的缺点当优点使用，是为微课而微课.某地教育局为推行微课，除了规定教师职称评定需要微课的等级达标，对于公开课也是规定必须使用微课，这和当初推广PPT一样，公开课凡不使用PPT者，一律不得评为优秀.过度使用、滥用微课就如烧菜不关注菜的品质，而只关注调味品一样，须知微课只是信息技术手段与教学相遇的产物，教学才是核心，教师才是根本，学生才是中心，切不可以偏概全，课堂使用微课必须适时、适中、适当，前面所举的几个例子都是在适当的时候使用微课，恰到好处，取得实效.

2.要正确理解微课的要义.

微课的定义很多，不同的人站在不同的角度给出不同的定义，但微课的要义应该是不变的.微课的“短小精悍”很好地解决了学习者的问题，把教材内容进行碎片化、情景化、重组整合（统称为“微课化”），把复杂的教材内容制作成可融合于课堂、移动地服务于开放教育和终生教育的视频单元［1］.显然，微课是围绕某个知识点（重点、难点、疑点）或教学环节而开展的教与学的过程，这就要求微课必须包含与教学主题相关的教学设计、素材、课件、教学反思、练习测试及学生反馈、教师点评等辅导性教学资源，以一定的组织关系和呈现方式共同“营造”一个半结构化、主题式的资源单元运用“小环境”［2］.但在实际应用中，有时不顾微课的系统性、整体性，把别人经典的赛课录像剪辑成若干个片段播放，称其为微课教学，他们认为那些在大赛中获奖的课就是好课，一段一段播放就是微课.还有一种情况是微课代替PPT，微视频上仅仅出现若干题目，教师把题目读一遍，就认为是一节微课，其实这样的微课和PPT、小黑板的作用相同，但花费的时间多，实在是一种浪费.前面所举的几例都是基于一个知识点来设计的，比如勾股定理的导入，情境设计巧妙；正方体的截面，几何画板演示形象、生动；勾股定理文化体现在勾股树美观大方，不设计这样的微课就很难达到如此效果，因为直达微课要义，所以微课教学事半功倍.

3.要提升课堂的互动性.

当学习知识移到了课前，课堂就成了内化知识的阵地，传统的课堂模式就必须做出变化.一方面，课堂不再是学生学习知识的主要场所，课堂的时间多了起来，另一方面，微课的碎片化必须利用课堂进行整合、系统化，以便于学生建构，所以课堂教学的互动成为可能，并成为课堂创新的追求.否则，微课不解决其交互性，就变成了信息技术下的灌输教育.在现实的课堂中，不少教师使用微课，仅仅是把学生的学习提前到课前，相当于让学生提前预习了一遍，课上教师仍然按照原来的模式讲课，学生按照教师的安排再学一遍，灌输教育一如既往，只是多了个形式而已.还有一种情况，微课安排在课前学习，课堂就变成了课堂练习，反复进行题目操练，美其名曰知识内化，这是一种典型的题海战术，短时间可能会提高学生的成绩，但长此以往，学科素养荡然无存.本文“分式”第一节课的课前和课中的衔接处理比较恰当，课前的学习为课中内化提供了基础和保证，课中以微课的内容为根据，通过师生互动、生生互动层层深入，逐步构建起完整的知识结构.

翻转课堂早已成为学习的潮流，但微课导学尚处在探索阶段，我们只有深刻理解微课产生的背景和意义，在实践中不断总结微课的使用规律，避免穿新鞋走老路，创新课堂教学形式，唯如此，微课导学才能焕发出勃勃生机.

1.胡铁生，等.我国微课发展的三个阶段以及其启示［J］.远程教育杂志，2013（4）.

2.李新运.中学微课教学导论［M］.长春：吉林出版集团有限责任公司，2015.