悬挂系统易损件跌落破损评价

李 辉，陈安军,2

(1.江南大学 包装工程系，江苏 无锡 214122；2.国家轻工业包装制品质量监督检测中心，江苏 无锡 214122)

Mindlin首次提出产品易损度概念，奠定了包装动力学的基础，但产品的易损度难以准确地确定[1]。在产品防护中，为更好地描述产品的损伤规律，Newton提出单自由度线性系统的破损边界理论[2]，Schell、Goff和 Pierce 尝试使用后锋锯齿加速度脉冲和半正弦脉冲测定产品破损边界[3–4]。Burgess发现产品受到的损害可以累加，提出疲劳破损边界概念[5–6]，为将破损理论进一步运用到实际工程，王振林提出位移易损度概念，建立位移破损边界曲线[7–8]。实际缓冲材料多为非线性，王志伟使用统一的方法研究线性和非线性系统在典型脉冲激励下的冲击响应谱和破损边界曲线[9–10]。由于跌落冲击是产品破损的主要原因之一，王志伟提出跌落破损边界概念，研究了线性和典型非线性系统的跌落破损边界曲线[11]。考虑到产品破损最先出现在易损件，文献[12–15]将包装系统的跌落破损边界扩展到考虑易损件的两自由度非线性系统，丰富了产品跌落破损边界理论。

缓冲包装研究中，人们注意到悬挂系统的几何非线性表现出良好的缓冲性能，徐筱分析了弹簧吊装系统跌落冲击响应特性[16]，吴晓研究了悬挂弹簧非线性减振系统的自振特性及基础位移激励下系统固有振动特性[17–18]，王蕾等研究了悬挂系统在典型脉冲激励下的冲击特性和破损评价[19–23]，在跌落工况下，宋爽等应用变分迭代法获得系统一阶近似解，探讨系统参数对跌落破损影响[24–27]；以上研究模型均未考虑易损件，因而悬挂系统的跌落破损评价需在考虑易损件的基础上进一步研究。

本文基于单自由度悬挂系统模型，建立考虑易损件悬挂系统动力学模型，引入无量纲参数，获得系统无量纲动力学方程，以系统参数和无量纲冲击速度为基本评价量，取频率比、阻尼比或悬挂角为第三评价量，构建易损件跌落破损边界曲面，探讨系统频率比，系统阻尼比以及悬挂角等参数对易损件跌落破损边界曲面的影响。

1 动力学模型

考虑易损件悬挂缓冲系统模型如图1（a）所示，其中m1为系统易损件质量，m2为产品主体质量，c1为易损件与产品连接处阻尼，c2为产品与基础连接处阻尼，k、k1分别为产品与基础连接和易损件与产品之间的弹性系数，φ0为悬挂角，l0为悬挂弹簧原长。

考虑系统跌落冲击动力学评价，假设系统从高度为H跌落，以易损件和主体静平衡位置为原点，垂直向下为正，易损件、主体受力分析如图1(b)所示，则易损件的动力学方程为

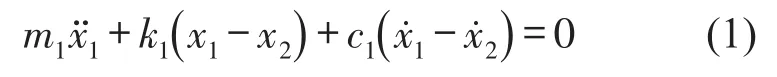
由文献[17–27]知，小变形条件下运用泰勒级数简化处理后，悬挂弹簧在垂直方向对主体的作用力

结合主体的受力分析，产品主体的动力学方程为

其中a0=sin2φ0，b0=(1-6sin2φ0+5sin4φ0)/2 。联立方程（1）和（3）可得考虑易损件悬挂系统动力学方程为

跌落冲击初始条件为

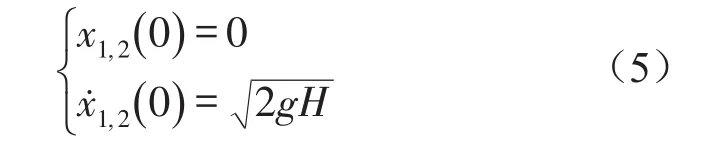
其中x1、x2为易损件及产品位移 ；为易损件及主体速度 ；为易损件及主体加速度；t为时间参数；H为系统跌落高度。

引入无量纲参数：易损件及主体的无量纲位移y1=x1/l0和y2=x2/l0，无量纲时间τ=t/T,易损件及主体的频率参数，主体周期参数T=1/ω2，系统无量纲动力学方程为

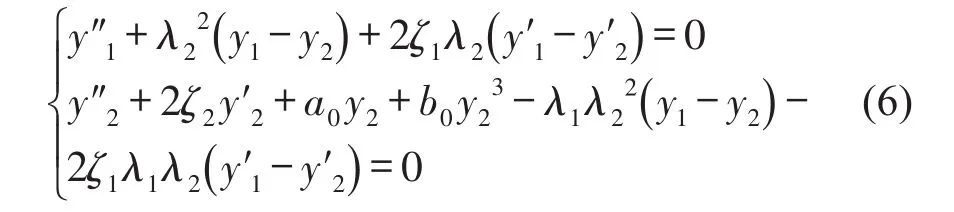
初始条件变为

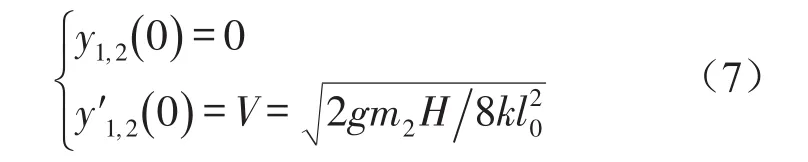
其中y′1=dy1/dτ、y″1=d2y1/dτ2分别为易损件的无量纲速度和加速度，y′2=dy2/dτ、y″2=d2y2/dτ2分别为产品无量纲速度和加速度，分别为易损件与产品间和产品与基础连接处的阻尼比，λ1=m1/m2为系统质量比，λ2=ω1/ω2为频率比。

图1 考虑易损件悬挂系统模型及受力分析图

2 易损件跌落破损评价

引入产品脆值Ac和系统参数β=l0/T2=8kl0/m2，由 d2x1/dt2=β(d2y1/dτ2)注意到当易损件加速度响应峰值达到其脆值时，即(d2x1/dt2)m=Acg，可获得易损件跌落破损评价方程

应用4阶龙格库塔法求解无量纲动力学方程（6），获得易损件无量纲最大加速度y′1m，当产品脆值Ac确定后，通过方程（8）转化为系统参数，构建易损件跌落破损评价。由于影响系统跌落冲击响应因素较多，构建跌落破损三维边界曲面可更直观反映相关参数对系统跌落冲击性能的影响。取系统参数作为第一评价参数；考虑到无量纲跌落冲击速度V与跌落高度H有关系，而H非常直观且易把握，因此将无量纲跌落冲击速度作为破损曲面的第二评价参数；频率比、阻尼比或系统悬挂角（几何参数）均为系统敏感参数，可作为破损边界曲面的第三评价参数。

2.1 频率比对易损件跌落破损的影响

取λ1=0.01，ζ1=0，φ0=60°，Ac=30，以系统参数β、无量纲冲击速度V和频率比λ2为评价量，不同阻尼比ζ2下，易损件跌落破损边界曲面如图3所示。

由图2知，小阻尼条件下（ζ2=0,0.05,0.07,0.1），较低频率比时，不仅安全区域小且存在波动现象；当系统频率比λ2＞5时，易损件跌落破损边界较为稳定，且安全区域较大。

2.2 阻尼比ζ2对易损件跌落破损的影响

取λ1=0.01，ζ1=0，φ0=60°,Ac=30；以系统参数β，无量纲冲击速度V和阻尼比ζ2为评价量，不同频率比λ2=5,6,7,9时,易损件跌落破损边界曲面如图3所示。

由图3分析知，一定质量比、频率比和系统悬挂角条件下，系统具有最佳阻尼比，但最佳阻尼比随其他参数的变化（本例为频率比参数）又表现出不同值。当系统阻尼比小于最佳阻尼比时，随阻尼比增加系统安全区域增大，当系统阻尼比大于最佳阻尼比时，随阻尼比增加，系统安全区域减小。

2.3 悬挂角对易损件跌落破损的影响

取λ1=0.01，ζ1=0，ζ2=0.05，Ac=30；以系统参数β，无量纲跌落冲击速度V和频率比λ2为评价量，φ0=60°,70°,80°,90°时，系统跌落破损边界曲面如图4所示。由图4知，相对线性系统（悬挂角为90°）降低悬挂角，破损边界曲面上移，产品安全区域增大，较低的悬挂角对提高产品的抗冲击性能有利。

为进一步研究悬挂角的影响，取λ1=0.01，λ2=5，ζ1=0，ζ2=0.05，Ac=30；以悬挂角为第三评价量，构建跌落破损评价曲面如图5，由图5可知，减少悬挂角，易损件安全区域增加。

3 结语

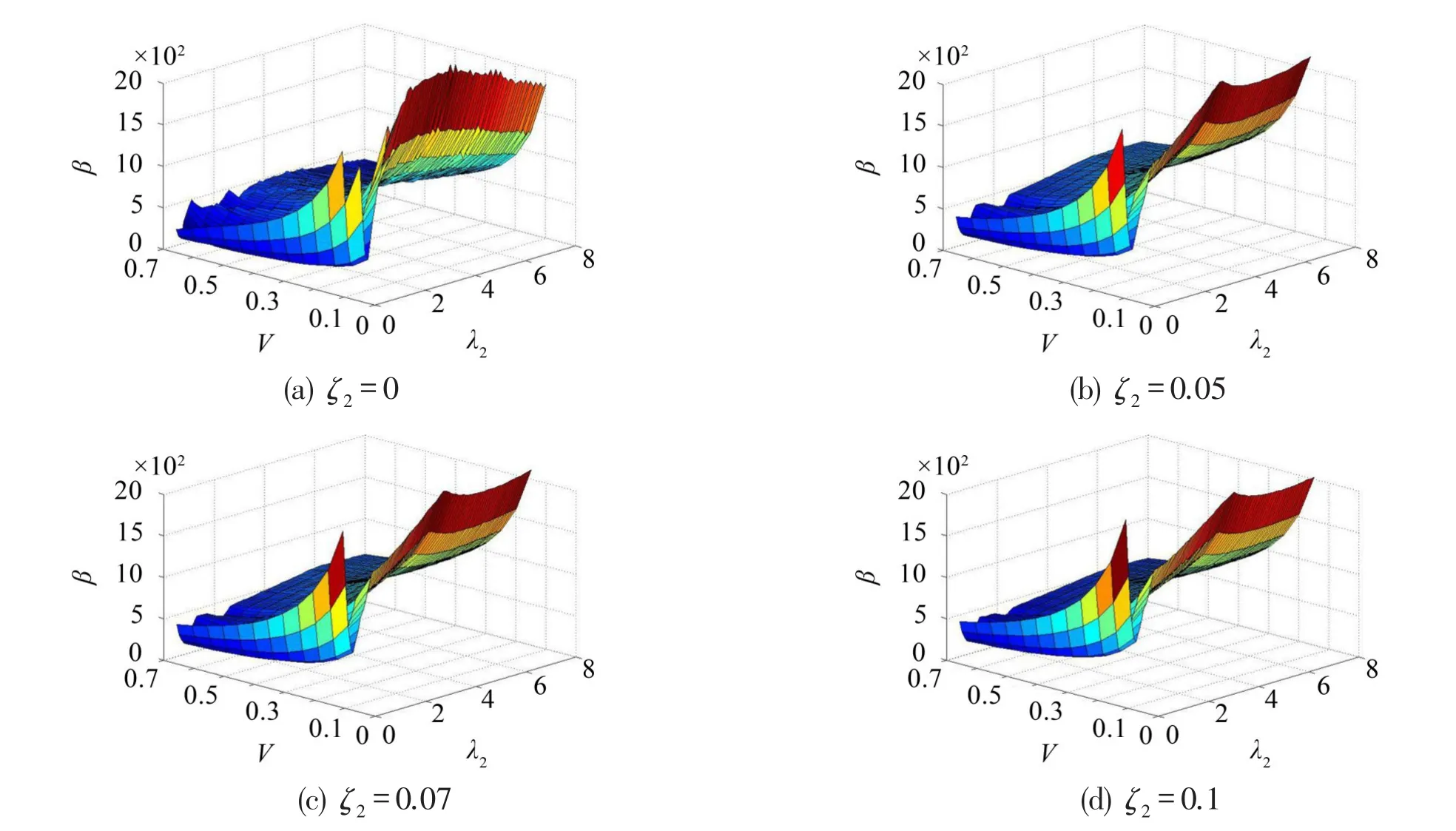
图2 考虑频率比λ2时易损件跌落破损边界曲面

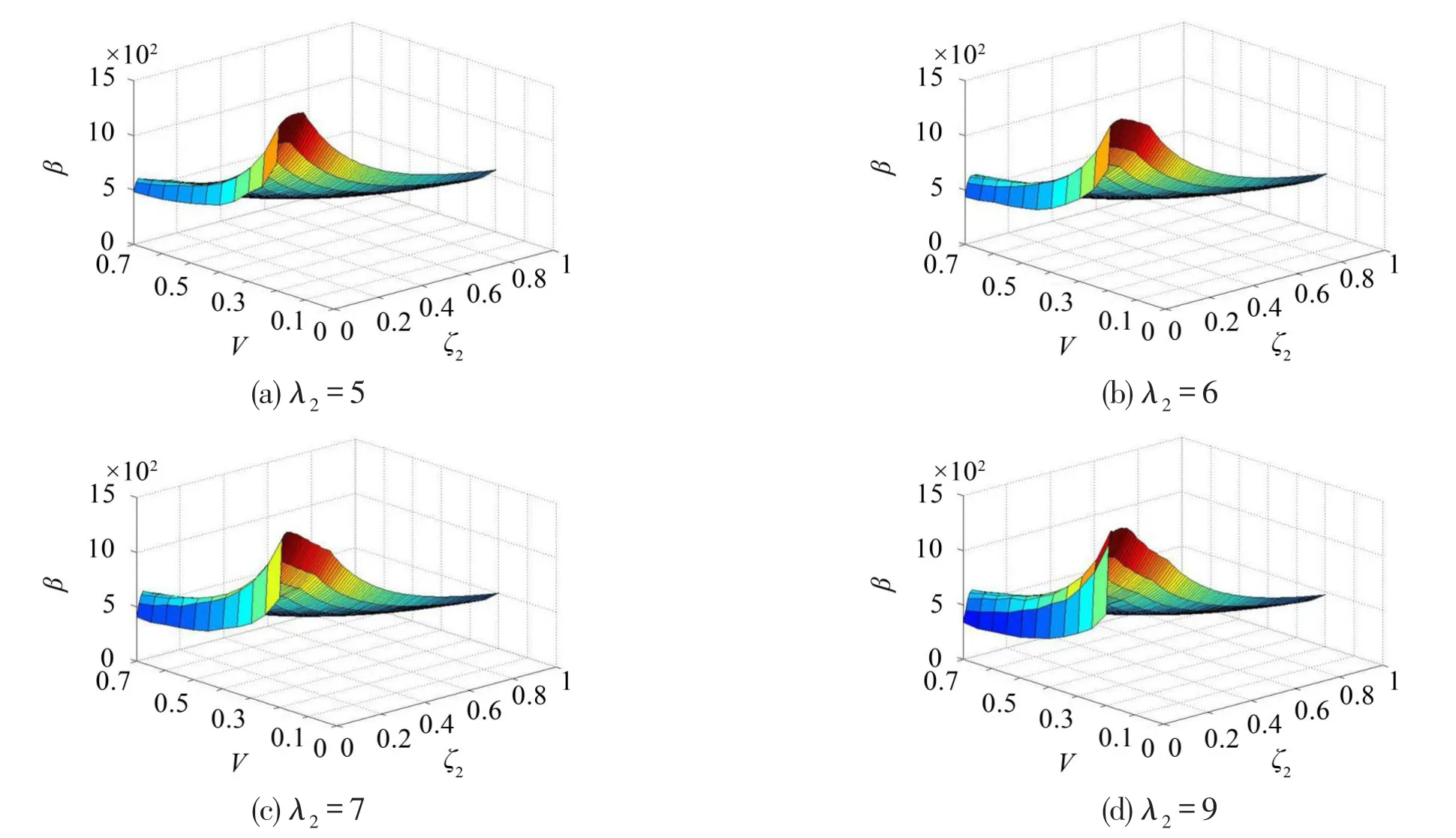
图3 考虑阻尼比ζ2时易损件跌落破损边界曲面

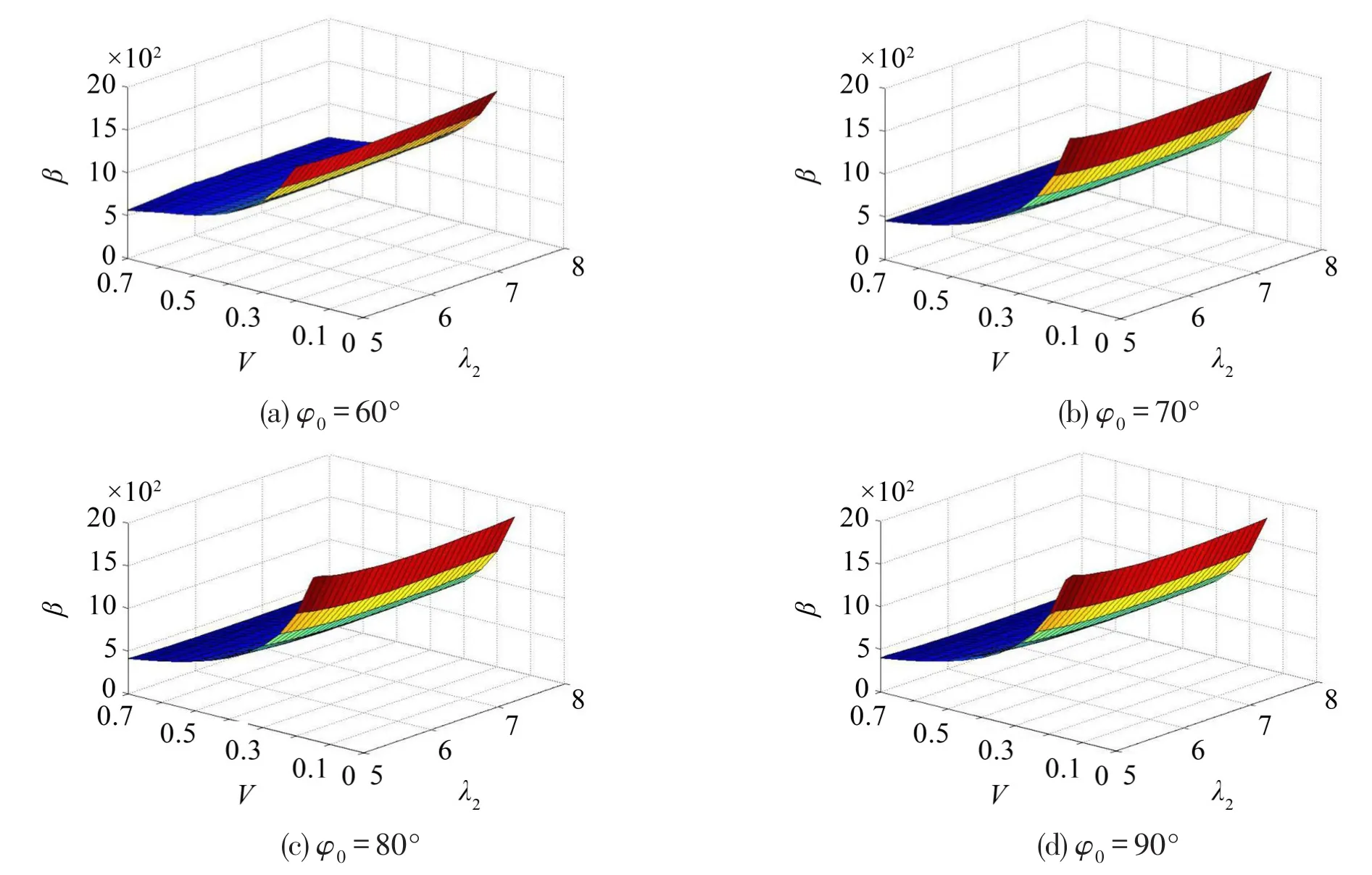
图4 悬挂角φ0对易损件跌落破损边界曲面的影响

基于单自由度悬挂系统模型，构建考虑易损件的两自由度系统力学模型，采用4阶龙格库塔数值分析方法求得易损件响应，并构建易损件跌落破损边界曲面。在跌落冲击条件下，影响易损件跌落破损边界面的重要参数包括系统的悬挂角、系统的频率比及阻尼比等，分析各参数对跌落破损边界曲面的影响。数值分析表明：

(1)易损件跌落破损边界曲面对系统的频率比敏感，相对于较低频率比条件下（λ2＜5）的系统安全区域，较高频率比（λ2＞5）条件下，系统的安全区域较大且较为稳定。因此，系统设计应远离低频率比区，选择较高的频率比值。

(2)易损件跌落破损边界曲面对系统的阻尼比同样敏感，系统存在最佳阻尼匹配，进一步分析表明，阻尼比在一定范围内，可对产品具有较好的保护作用。该范围在小阻尼条件下成立，同时注意到，阻尼比并非越大越好。

图5 考虑悬挂角φ0时易损件跌落破损边界曲面

(3)与线性系统相比，较小的悬挂角条件下，易损件更安全，但同时也应关注当悬挂角较小时，系统的位移响应增加，可能出现触底问题。

(4)系统的特征参数和无量纲跌落冲击速度对产品的保护具有重要的意义。较低的系统参数可使系统承受较大的无量纲冲击速度，由系统参数β=8kl0/m2知,较低的系统参数可以选择较小的弹性系数和悬挂弹簧的长度，但同时注意无量纲冲击速度增加，且可能产生较大的位移，出现触底问题。因此，悬挂系统的设计为更好地保护产品，需综合系统相关参数的选择。

[1]MINDLIN R D.Dynamics of package cushioning[J].Bell System Technical Journal,1945,24(3,4):353-461.

[2]NEWTON R E.Fragility assessment theory and practice[R].Monterey Research Laboratory,Inc.Monterey,California,1968.

[3]SCHELL E H.Evaluation of a fragility test method and some proposals for simplified methods[J].Shock Vibration Bull,1969,40(6):133-152.

[4]GOFF J W,PIERCE S R.A procedure for determining damage boundary[J].Shock Vibration Bull,1969,40(6):127-131

[5]BURGESS G J.Product fragility and damage boundary theory[J]．Packaging Technology and Science,1988,15(10):5-10.

[6]BURGESS G J.Effects of fatigue on fragility testing and the damage boundary curve[J].Journal of Testing and Evaluation,1996,24:419-424.

[7]WANG Z L,WU C F,XI D C.Damage boundary of a packaging system under rectangular pulse excitation[J].Packaging Technology and Science,1998,11:189-202.

[8]王振林，吴长富，奚德昌.物品包装系统位移损坏边界[J].振动工程学报，1998，11(4)：434-442.

[9]WANG Z W,HU C Y.Shock spectra and damage boundary curves for nonlinear Package cushioning system[J].Packaging Technology and Science,1999,12(5):207-217.

[10]WANG Z W.Shock spectra and damage boundary curves for hyperbolic tangent cushioning systems and their important features[J].PackagingTechnologyand Science,2001,14:149-157.

[11]WANG Z W.On evaluation of product dropping damage[J].Packaging Technology and Science,2002,15(3):115-120.

[12]WANG J,JIANG J H,LU L X,et al.Dropping damage evaluation for a tangent nonlinear system with a critical component[J].ComputersandMathematicswith Applications,2011,54:1979-1982.

[13]WANG Z W,JIANG J H.Evaluation of product dropping damage based on key component[J].Packaging Technology and Science,2010,23:227-238.

[14]JIANG J H,WANG Z W.Dropping damage boundary curvesforcubic and hyperbolictangentpackaging systems based on key component[J].Packaging Technology and Science,2012,25:397-411.

[15]WANG J,DUAN F,JIANG J H.Dropping damage evaluation for a hyperbolic tangent cushioning system with a critical component[J].Journal of Vibration and Control,2012,18(10):1417-1421.

[16]徐筱.悬浮式缓冲包装系统分析与研究[D].西安：西安理工大学，2005．

[17]吴晓，杨立军.悬挂弹簧几何非线性减振系统的固有振动特性[J].振动与冲击，2008，27(11)：71-72.

[18]吴晓，罗佑新，杨立军.基础位移作用下悬挂弹簧的非线性固有振动[J].北京理工大学学报，2009，29(12)：1041-1043.

[19]WANG L,CHEN A J.The damage boundary curve of the suspension packaging system under rectangular pulse[J].Applied Mechanics and Materials,2012,5(107):70-73．

[20]WANG L,CHEN A J.The shock response spectra of the suspension packaging system under rectangular pulse[J].Journal of Applied Packaging Research,2012,5(4):237-246.

[21]王蕾，陈安军.悬挂式弹簧包装系统的冲击特性研究[J].包装工程，2011，32(9)：33-36.

[22]王蕾，陈安军.矩形脉冲激励下悬挂式弹簧系统冲击特性的研究[J].振动与冲击，2012，31(11)：142-144.

[23]王蕾.悬挂式缓冲包装系统动力学性能的研究[D].无锡：江南大学，2012.

[24]宋爽，陈安军.基于变分迭代法的悬挂式弹簧系统的跌落破损评价[J].包装工程，2013，34（13）：36-39.

[25]宋爽，王蕾，陈安军.悬挂式弹簧系统跌落冲击问题的变分迭代法[J].噪声和振动控制，2013，33（6）：36-39.

[26]SONG S,CHEN A J.Variational iteration method of dropping shock response forthe suspension spring packaging system[J].ShockandVibration,2015,408674(6).

[27]SONG S,DUAN N N,CHEN A J.Application of variational iteration method for dropping damage evaluation of the suspension spring packaging system[J].Abstract andAppliedAnalysis,2014,385404(7).