多孔流体阻尼式动力吸振器的动力学建模及实验研究
2018-03-03谢溪凌刁建超张志谊
卢 琦,谢溪凌,刁建超,张志谊
(1.上海交通大学 振动、冲击、噪声研究所,上海 200240;2.上海交通大学 机械系统与振动国家重点实验室,上海 200240)
长期以来,低频扰动(如地震)给人们带来很大的困扰。通信设备在生产生活中发挥着不可替代的作用,然而通信设备中敏感器件在外界扰动(如地震)下可能无法正常工作,抑制敏感器件振动因此受到关注[1–2]。
由于被动式动力吸振器具有成本低,可靠性高,且不需外界能量等优点而被广泛应用于工程减振中,采用动力吸振技术对通信敏感器件低频振动进行抑制也是优先选择之一。传统的动力吸振器阻尼一般采用橡胶材料,由于橡胶存在易老化、有效温域较窄等问题,其应用受到一定局限[3]。新型的阻尼形式有电涡流、磁流变等。但电涡流阻尼效率低、体积尺寸较大,磁流变阻尼难调控、稳定性差,并且此类阻尼应用于通信敏感器件会产生一定的干扰[4–5]。而黏滞流体阻尼具有安全有效、成本低等特点,被广泛应用于各类阻尼器。
常见黏滞流体阻尼结构可分为间隙式和孔隙式。在镗杆的减振中,一般在质量块与镗杆之间充满间隙式黏滞流体作为阻尼实现形式应用于动力吸振器[6–7]。韦联对镗杆内藏的间隙式阻尼结构动力吸振器参数进行了优化,并提出通过旋转螺塞的方法来调节阻尼液的等效阻尼比[8];张维等对应用于船舶轴系的流体动力吸振器设计参数进行了优化分析,并通过仿真计算验证其优化效果[9]。这些研究都是针对间隙或单孔阻尼结构,阻尼调节不便。
本文提出一种多孔流体阻尼式动力吸振器,建立吸振器阻尼模型,分析阻尼孔参数对沿程阻尼与局部阻尼力的影响规律,给出吸振器刚度和阻尼的设计方法,并对吸振器的减振效果进行仿真和实验。
1 动力吸振器设计
1.1 动力吸振器工作原理
考虑如图1所示的带有动力吸振器的系统,其运动方程为

式中M、m分别为主振动系统和吸振子质量,KM、Km分别为主振动系统和吸振子的刚度,xM、xm分别为主振动系统和吸振子的位移,C为吸振子的阻尼,u为激励位移。

图1 吸振器系统动力学模型
求解简谐基础激励下的系统稳态响应,可以得到系统的振幅比如下[6]

式中XM、Xm的分别为主结构系统和吸振器振子的位移实数振幅。U为激励位移振幅;为主振动结构的固有角频率为动力吸振器的固有角频率为吸振器质量/主结构质量;rω=ω/ωn为激励频率比;f=ωa/ωn为固有频率比;cc=2mωn为临界阻尼系数;ξ=c/cc为阻尼比。
1.2 动力吸振器的最优参数
(1)最优同调频率
根据定点理论[10],为达到最优同调,两定点响应相等,可以得到

(2)最优阻尼比
为使主结构振动幅值最小,不仅需要满足两定点等高,还需要使定点处为振幅倍率曲线上的最高点,则

取二者平均值可得到最优阻尼比,即

2 吸振器刚度与阻尼设计
2.1 刚度与阻尼的计算
本文中吸振器刚度由弹簧产生,对于直线圆柱弹簧,弹簧刚度的计算公式[11]
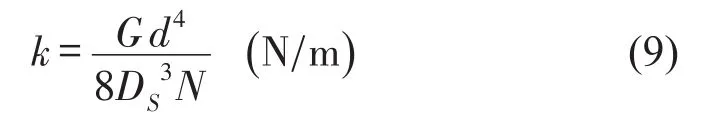
式中G为材料的切变模量;d为弹簧线径;N为工作有效圈数;DS为弹簧中径。
阻尼由吸振子上的开孔产生,为多孔流体阻尼。多孔流体阻尼中的沿程阻尼力可由下式计算获得[12]

式中CH为沿程阻尼系数,uH为流体动力粘度;L为振子宽度;R为振子半径;振子上开有S组孔径不同的小孔,第i组圆孔的圆孔半径ri,数量为ni,V为活塞运动速度。
流体阻尼中的局部阻尼由一组扩张和收缩孔产生,根据扩张和收缩孔的阻尼计算公式[13],可以得到局部阻尼力为
式中B为局部阻尼系数,ρ为流体密度;D为振子直径,第i组圆孔的圆孔直径di,数量为ni,振子有效截面积为A1,V为活塞运动速度。
为探究阻尼孔面积比对阻尼力的影响,在保证其它参数一致的条件下,讨论阻尼力随阻尼孔面积比的变化情况。相关参数如表1所示。
图2、图3分别为阻尼孔径d=0.004 m、d=0.01 m时,沿程阻尼力FC与局部阻尼力FB随阻尼孔面积比的变化曲线。

图2 阻尼力与面积比的关系(d=0.004 m)

图3 阻尼力与面积比的关系(d=0.01 m)
从图2、图3可以看出随阻尼孔面积比增大,阻尼力减小,其中沿程阻尼力衰减速度小于局部阻尼力;对比图2、3可知,在其它参数相同的条件下,阻尼孔直径越小,振子上能够生成的阻尼孔数量越多,阻尼孔能够达到的面积比越大,沿程阻尼力占总阻尼力比重就越大。
由于沿程阻尼力是速度的线性函数,而局部阻尼力是速度的非线性函数,根据一个周期内能量耗散等效的原则线性化[14],可得局部等效线性阻尼系数为
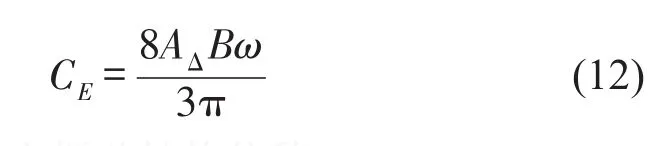
式中AΔ为振子与主振动结构位移差的振幅值,B为局部阻尼系数。因此,系统的阻尼系数C可以表示为

2.2 吸振器结构及参数
动力吸振器采用往复活塞式结构,吸振器模型和实物如图4所示,包括缸体、多孔吸振子(活塞)、振子弹簧和流体(水或硅油)。吸振器与被保护的主振系统(含主振质量和复位弹簧)固定连接,主振系统通过滑轨置于基础之上。活塞上有蜂窝阻尼孔,活塞与缸体通过圆柱弹簧连接,当吸振器受外激励振动时,活塞运动使流体流经阻尼孔,产生阻尼力,并与振子弹簧的恢复力共同作用,抑制主振质量的振动。
吸振目标频率为2 Hz,主振动系统质量M=6.88 kg,包括敏感器件质量m1=2.5 kg、吸振缸体及硅油质量m2=4.38 kg,取质量比u=0.36,根据最优参数设计公式(5)、式(8),可以确定吸振器的刚度和最优阻尼系数。根据阻尼结构设计式(10)-式(13),确定阻尼孔相关参数。吸振系统的参数如表2所示。
根据表2所示的吸振系统参数,系统加速度传递率和激励频率的关系曲线如图5所示。
从图中可以看出,当阻尼比在最优阻尼比附近时(ξ=0.23),位移传递率与频率的关系曲线表现出明显的吸振特性,在2 Hz左右出现了波谷。随阻尼系数的继续增大,曲线趋势由两个波峰逐渐变成一个波峰,且阻尼系数越大,峰值越高。

表1 阻尼孔设计相关参数

图4 吸振器模型和实物图

表2 吸振系统参数

图5 不同阻尼系数下的位移传递率
3 实验测试
3.1 实验方案
测试系统如图6所示,系统包括振动台、加速度传感器、信号调理器和动态信号分析系统等。

图6 实验原理图
将振动加速度传感器A放置于与振动台固连的板上,用来采集主振系统所受的外界激励,将加速度传感器B放置于吸振器缸体上,采集主振系统振动信号。
实验时分别以水和不同黏度的硅油(20 cs、50 cs、80 cs)作为流体介质,测试单频激励(1.5 Hz~2.8 Hz)下主振质量有、无动力吸振的时域响应。单频激励时间32 s,分析带宽16 Hz,频率分辨率0.062 5 Hz。取稳态响应的RMS值作为输入、输出加速度值,计算出对应各单频的主振系统的加速度传递率,通过描点法绘出传递率曲线,用以衡量吸振器的减振性能。
3.2 实验结果与分析
图7所示为不同介质下有、无动力吸振的加速度传递率曲线。
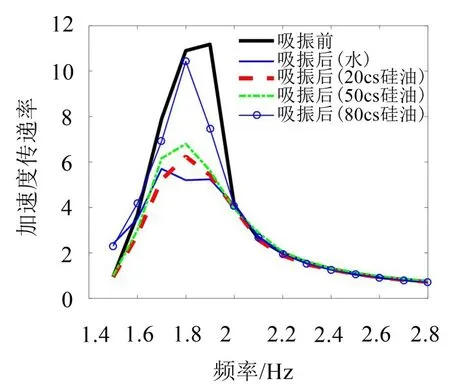
图7 不同介质中有、无动力吸振的加速度传递率曲线
从图中可以看出,在水介质中,激励频率1.6 Hz~2 Hz内,吸振器有明显减振效果,吸振前的加速度传递率最大值为11.2,对应的吸振后的加速度传递率为5.2,传递率下降53%左右,表明多孔流体阻尼式动力吸振器在1.8 Hz附近具有较好的吸振效果。在20 cs、50 cs硅油介质下吸振器也有明显的减振效果,最大加速度传递率分别下降44.6%和42.9%。此时加速度传递率曲线表现为单峰,说明阻尼系数偏大。在80 cs硅油介质下,吸振器无明显减振效果,最大传递率下降6.7%。各介质对应的吸振前后的加速度传递率如表3所示。

表3 吸振前、后时域最大加速度传递率对比
实验中实际阻尼偏大,这是由于活塞与缸体内壁之间存在摩擦。摩擦对应的等效黏性阻尼系数可表示为[15]

式中uf为振子与缸壁的摩擦系数,m为振子质量,ρ为流体密度,V为排水量,AΔ为振子与主振动结构相对位移幅值。若考虑摩擦效应,以20 cs硅油介质为例,摩擦力在2 Hz左右的等效阻尼是56 N·s/m,阻尼比为0.72,实测与仿真传递率曲线如图8所示。
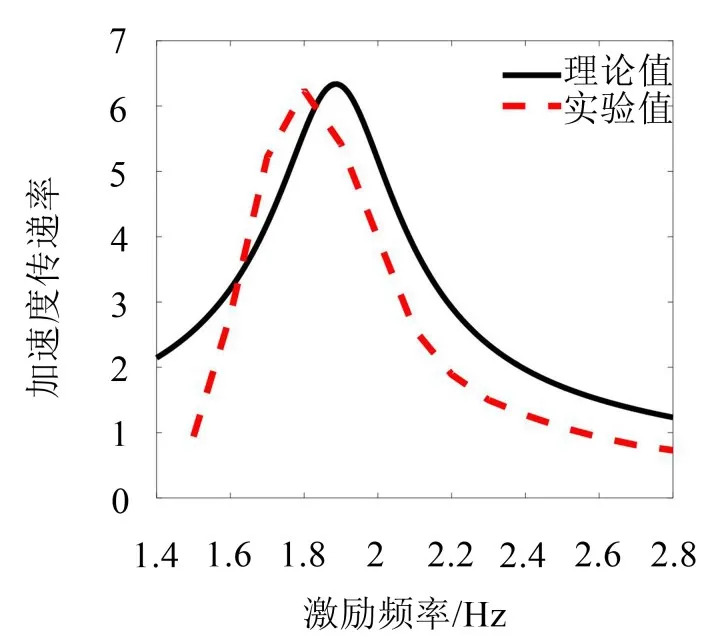
图8 20 cs硅油介质传递率实验-仿真结果对比
4 结语
本文研究一种多孔流体阻尼式动力吸振器,基于能量等效原则,对多孔流体阻尼进行计算,进而对吸振器结构进行优化设计,最后对多孔流体阻尼式动力吸振器的性能进行实验验证。测试结果表明,吸振器的吸振频率在1.6 Hz~2 Hz之间,吸振后的加速度传递率最大可下降53%左右。
(1)在流体黏性很小时,仍具有很好减振效果,说明局部阻尼起了非常重要的作用。
(2)随着流体黏度的增加,减振效果呈下降趋势,在黏度为80 cs时,吸振器基本没有减振效果。
阻尼孔数量的影响以及两种类型阻尼的作用仍需进一步研究。
[1]夷红志,关旭东,郑懿,等.基础环境振动对精密仪器的影响[J].机械工程师,2015,11:34-35.
[2]方重,俞洁勤.网络、通讯设备的办公室、运输和地震环境振动试验及标准[J].振动与冲击,2005,24(1):124-125.
[3]刘高君.橡胶阻尼材料的老化行为与寿命预测研究[D].青岛:青岛科技大学,2013.
[4]杨毅青,裴行政,刘强.被动阻尼减振技术及数控加工应用[J].航空制造技术,2016,513(18):16-23.
[5]陈忠海,杨全,宁响亮,等.磁流变阻尼器的设计、试验及其减振性能研究[J].地震工程与工程振动,2014,34(1):204-210.
[6]胡李波,王民,李刚.动力减振镗杆的减振性能研究[J].机械设计与制造,2009(1):131-133.
[7]秦柏.阻尼动力减振镗杆动态特性仿真与优化设计研究[D].哈尔滨:哈尔滨理工大学,2009.
[8]韦联.减振镗杆的动力学仿真及其参数优化[D].成都:西华大学,2011.
[9]张维,李天匀,朱翔.船舶轴系纵振的流体动力吸振优化分析[R].促进中部崛起专家论坛暨湖北科技论坛,武汉,2009.
[10]背户一登.动力吸振器及其应用[M].北京:机械工业出版社,2013:26-27.
[11]闻邦椿.机械设计手册[M].北京:机械工业出版社,2015:16-17.
[12]周云.黏滞阻尼减震结构设计[M].武汉:武汉理工大学出版社,2006:98-100.
[13]黄卫星,李建明,肖泽仪.工程流体力学[M].2版.北京:化学工业出版社,2009:98-100.
[14]何玲.流体阻尼器特性及其对整星隔振性能影响的研究[D].哈尔滨:哈尔滨工业大学,2007.
[15]屈振德.机械振动手册[M].北京:机械工业出版社,1992:44-46.
