时变负载转矩伺服电机驱动的连铸结晶器振动位移系统补偿控制

马 壮 方一鸣 李建雄 刘 乐

1.燕山大学工业计算机控制工程河北省重点实验室，秦皇岛，0660042.国家冷轧板带装备及工艺工程技术研究中心，秦皇岛，0660043唐山学院智能与信息工程学院，唐山，063000

0 引言

连铸结晶器是钢铁连铸自动化生产过程中的关键设备之一，其振动波形、振动频率、拉坯速度等参数直接影响着铸坯质量。目前，连铸结晶器按照振动控制方式主要分为采用正弦振动与非正弦振动[1-4]两大类；按照驱动方式主要分为是伺服驱动和非伺服驱动两大类。本文以伺服电机驱动的连铸结晶器非正弦振动装置[5]为研究对象，该装置采用单方向连续转动控制方式，不仅有效避免了电机频繁的正反转启停，且具备节能降耗、结构简单、可维护性好等优点[6]，但其系统的负载具有时变等不确定性，这在某种程度上制约了系统控制精度的进一步提高。

近年来，国内外关于伺服电机驱动系统的研究，主要针对控制精度、跟踪精度和抑制扰动等方面。文献[7]针对伺服系统存在外部扰动和参数不确定性等特点，采用预测控制方法设计了控制器，保证了闭环系统对转速的精确跟踪和对电机电流的输出控制。文献[8]提出在伺服系统位置前馈控制的基础上，引入位置环微分负反馈控制策略，这样既能保证系统无超调快速响应，又不影响位置前馈跟踪性能。文献[9]采用模糊控制与神经网络相结合，实现连铸结晶器非正弦振动系统的跟踪控制，仿真结果验证了所设计的方案能提高非正弦振动系统跟踪控制性能和鲁棒性。文献[10]应用无源性控制理论和方法，研究了在负载转矩和期望转矩任意时变的情形下异步电动机期望转矩的渐近跟踪控制问题。文献[11]提出以转速、负载转矩为观测对象的扩展滑模观测器，对观测的负载转矩进行前馈补偿，克服了负载时变对控制性能的影响。文献[12]采用非奇异终端滑模的负载观测器，将观测值补偿到系统的控制器中，从而增强了系统的鲁棒性，并提高了跟踪精度。文献[13-14]引用自抗扰控制技术在线估计转矩扰动，进一步提高了伺服控制精度。然而，针对仅具有位移传感器的连铸结晶器振动控制系统来说，因其单方向、变角速度旋转产生的伺服电机位置转角的控制问题，前述方法并不能直接采用。

本文分析并建立伺服电机驱动的连铸结晶器非正弦振动控制系统数学模型，对结晶器振动位移与伺服电机角位移之间的逆解非唯一问题将采用分段函数映射的方法；针对结晶器控制系统的时变负载转矩特性，采用扩张状态观测器对时变负载转矩和伺服电机转速进行观测，并将其输出的观测值引入到Backstepping控制器中进行补偿，以抑制时变扰动与负载突变引起的系统性能的降低。

1 伺服电机驱动的连铸结晶器系统数学模型

1.1 伺服电机驱动的连铸结晶控制系统描述

(a)系统振动装置样机原型

(b)系统振动装置示意图图1 伺服电机驱动的连铸结晶器振动装置样机及示意图Fig.1 Vibration device prototype and schematic diagram of continuous casting mold driven by servo motor

本文研究的伺服电机驱动的连铸结晶器振动装置示意图如图1所示。伺服电机通过联轴器、减速器、偏心轴以及连杆等机械传动机构，实现对结晶器振动台的驱动控制。

伺服电机驱动的连铸结晶器位移控制系统振动装置原理为：首先，结晶器位移振动控制系统根据连铸拉坯速度与给定位移振动波形计算出伺服电机的转速；其次，将转速传送给伺服电机控制器，通过伺服电机控制器与伺服电机形成转速与电流的双闭环系统，跟随系统转速的给定；最后,通过机械传动机构完成结晶器位移振动控制系统输出。其系统输入输出规律为：当伺服电机恒速运转时，结晶器为正弦振动；当伺服电机变速运转时，结晶器为非正弦振动。

本文主要分析负载的时变特性对系统位移控制精度的影响，并进行补偿控制研究。其振动装置的负载主要包括钢水、结晶器本体、振动台的质量等。同时，结晶器非正弦(含正弦)振动过程中负载存在加速度，也会产生力矩；结晶器中铁水的多少也将会引起负载的波动。

1.2 系统模型描述

1.2.1 伺服电机双闭环系统部分模型

伺服电机驱动的连铸结晶器模拟振动系统采用的是永磁同步电动机(PMSM)；控制器为西门子S120驱动控制器，构成伺服电机转速和电流环双闭环控制系统，如图2所示。

图2 伺服电机驱动器控制的电流与 转速双闭环控制原理图Fig.2 Principle diagram of current and speed double close-loop for servo motor driver

本文的伺服电机模型采用的是d-q坐标系下状态方程的形式[12]：

(1)

式中，n为伺服电机输出转速；ud、id分别为d轴电压和电流；uq、iq分别为q轴电压和电流；J为转动惯量；B为黏性摩擦系数；TL为负载转矩；p为磁极对数；L、Rs、ψf分别为伺服电机等效的电感、磁阻和磁链。

1.2.2 机械传动机构部分模型建立

连铸结晶器振动装置机械传动机构部分(图1b)主要由减速器、偏心轴及连杆等组成。假设联轴器、偏心轴以及连杆机构为刚性连接，并忽略其非线性因素，这里仅考虑减速器的测量误差以及齿轮间隙磨损造成的减速比变化的影响，本文采用减速器的理想减速比i=5.113 5。结晶器连杆机构振动位移模型为

xp=hsinθm

(2)

式中,h为连铸结晶器振动位移,h=3 mm；θm为偏心轴的位置转角。

θm与伺服电机输出的角速度ω的关系表达式如下：

ω=2πnm/60=2πn/(60i)

(3)

(4)

式中，ω为伺服电机输出的角速度；nm为伺服电机经减速器后输出的转速。

由式(2)～式(4)可知，振动位移模型为

(5)

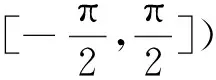
(6)

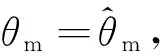
1.2.3f(·)函数关系的确立

结晶器位移振动范围在[-h,h]，其逆解与角位移并不是一一对应的。为使其相对应，本文提出了一种分段映射函数法f(·)，建立区间内偏心轴角位移与结晶器位移的一一对应关系，其原理如图3所示。图3a中结晶器振动位移h=3 mm，在一个周期范围内划分了4个时间段，即为t1、t2、t3、t4。

(a)振动位移及其绝对值曲线

(b)期望角位移和|xp|/h反正弦曲线图3 结晶器振动位移与角位移变换原理图Fig.3 Conversion principle diagram between mold vibration displacement and angular displacement

在结晶器控制系统的偏心轴零位确定为初始值为0的情况下，其振动波形如图3a所示；本系统的伺服电机单方向旋转的角位移与量纲一振动位移|xp|/h的反正弦函数关系如图3b所示。其变换推导过程如下。

(1)根据结晶器第一个周期的振动位移及其绝对值推导角位移与|xp|/h之间的关系，如下式所示:

(7)

其中，ti与ω的关系为

(8)

(2)引入变量k，在0≤ωt≤ωt0区间，其值为1；在ωt0≤ωt≤ωt1区间，k=2；其中j=i+1,以此类推，通过式(7)可归纳出：

f(xp)=

(9)

ωti<ωt<ωtj

(3)变量k的初始值为1，其k←k+1的更新条件为

(|xp(t)|-|xp(t-1)|)·(|xp(t+1)|- |xp(t)|)<0

(10)

(4)更新k后，返回步骤(2)即可。

定义1θ(t)是伺服电机驱动的连铸结晶器非正弦控制装置的角位移输出，A为关于振动波形偏斜率α的表达式。θ(t)为自变量时间t的连续函数，t∈[0,∞)，其表达式如下：

θ(t)=ωt+Asinωt

(11)

定理1 对于结晶器振动位移xp=hsinθ(t)，其中h>0。在t∈[0,∞)的任意时刻，关于f(xp)的表达式，式(9)是连续函数，且θ(t)与xp一一对应。

证明：

(12)

在计算映射函数的右极限时，k更新为k+1，此时极限为

(13)

故可得

(14)

由式(14)可知，即f(xp)在此点为连续函数。同理，当k为偶数时，f(xp)也为连续函数。因此f(xp)为映射函数。证毕。

(2)唯一性证明。由定义1可知：θ′(t)=ω+Aωcos(ωt)≥ω-Aω=ω(1-A)>0,因此，θ(t)为单调增函数。现仅须证明f(xp)为单调增函数，即可证明f(xp)与θ(t)是一一对应的。当k为奇数时，f(xp)的导数为

(15)

同理，当k为偶数时，f(xp)的导数为

f′(xp)=ω(1-A)>0

(16)

证毕。

由式(13)可知，在ω=13.61 rad/s，A=0.4的情况下。图4所示为角位移映射函数与实际位移实时跟踪曲线。由图4可以看出，实际角位移经映射函数转换后得到的曲线，具有很高的转换精度，同时表明了本方法的可行性。

图4 映射函数f(·)和实际角位移跟踪曲线Fig.4 Curve of mapping function f(·) and the actual angular displacement

因电流环均考虑在伺服电机驱动器之内，经整定采用PI调节器，故此部分不再赘述。

(17)

式中，D(t)为含有负载扰动Δd和参数摄动ΔB的复合扰动。

负载转矩(TL+Δd)具有时变特性，Δd为时变负载扰动的不确定项，Δd满足下式：

sup‖Δd(t)‖=δ<+∞t∈[0,+∞)

(18)

式中,δ为已知常数。

2 控制器设计与稳定性分析

首先，针对负载时变扰动，采用扩张状态观测器进行观测；然后，采用Backstepping控制方法进行位置环控制器设计，并进行稳定性分析。系统控制结构图如图5所示。

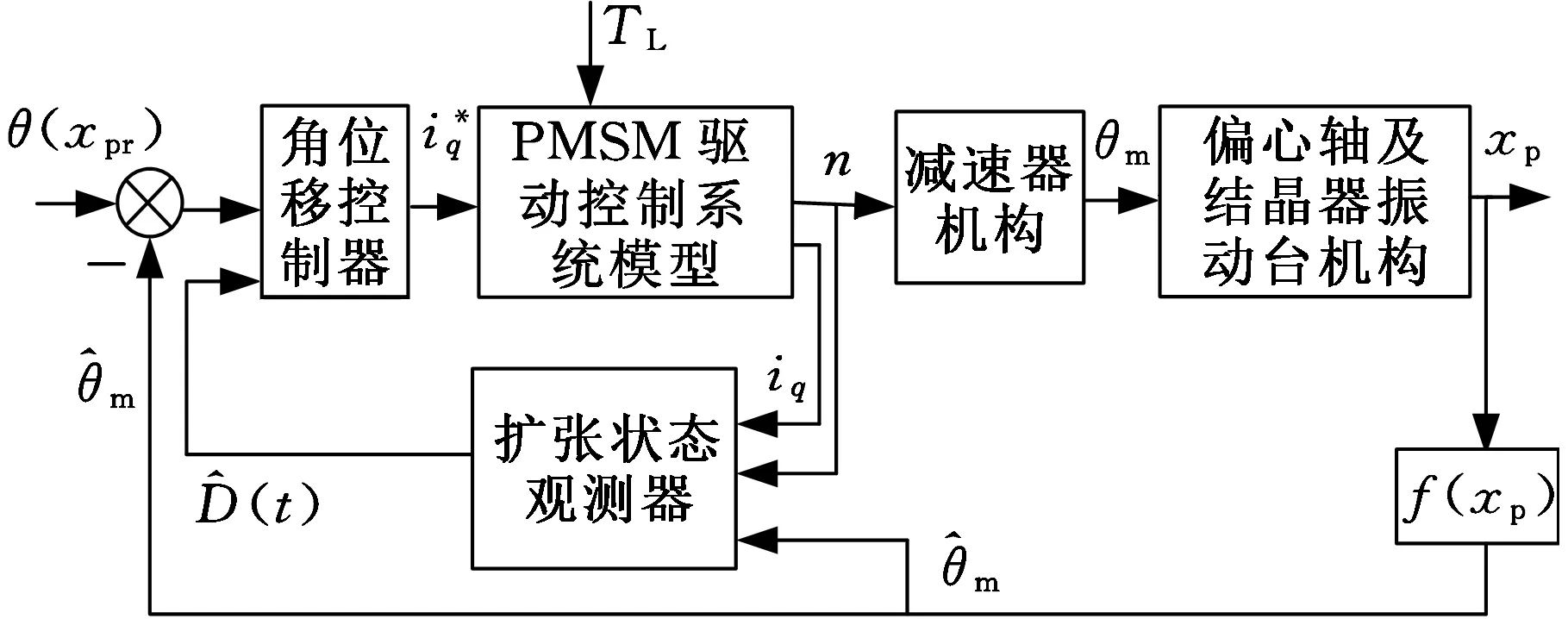
图5 伺服电机驱动的连铸结晶器位移控制系统原理图Fig.5 Control system principle diagram of continuous casting mold driven by servo motor for displacement

2.1 时变负载状态观测器的设计

在结晶器控制系统中，针对式(18)中的负载转矩不确定项，拟采用带有动态补偿律的非线性扩张状态观测器[15]，表达式如下:

(19)

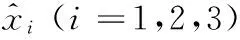
g(·)的表达式如下：

(20)

式中，exp为自然对数。

参数矩阵K=[k1k2…kn+1]可由下式中的期望极点来确定：

(21)

式中，pi为预设极点;K为状态观测器参数矩阵；I为单位矩阵;s为拉普拉斯算子。

2.2 控制器设计

由式(19)，定义系统状态误差向量E=(e1,e2)=x-xd，xd=(x1d，x2d)，x、xd分别为系统状态向量、期望状态向量，则系统误差模型为

(22)

采用Backstepping控制方法完成式(22)控制器设计，步骤如下：

根据式(22)的第1式构造Lyapunov函数V1为

(23)

令虚拟控制量σ=K1e1+e2(K1>0为可调参数)，则式(23)的微分为

(24)

针对子系统式(22)的第2式，选取实际控制量u为

(25)

式中，K2为可调参数，K2>0。

构造正定Lyapunov函数V2为

(26)

对V2求一阶导数：

(27)

根据李雅普诺夫稳定性理论，伺服电机驱动的连铸结晶器振动控制系统在所设计控制器(式(25))的作用下是全局渐近稳定的。

3 仿真研究

为了验证所设计算法的有效性，针对前文中设计的控制器及非线性处理方法进行时变负载转矩的结晶器振动控制系统仿真研究。图1中的减速器的减速比i=5.114 5。伺服电机采用的是德国Siemens的1FT6134-6，其具体参数见表1。

表1 永磁同步电机参数

电流d、q轴的PI调节器结构为

(28)

式中,Kp为比例调节系数;τ为积分调节时间。

经系统参数整定，式(28)中的参数分别为KP=12.982，τ=0.002 s。

本文采用的扩张状态观测器，预设极点为三重根p1,2,3=-5，根据式(21)计算可得：k1=75，k2=75，k3=125。

结晶器的给定角位移信号为

θ*=ωt-Asin(ωt)

(29)

式中，f为连铸结晶器非正弦振动频率,f=130 Hz。

文献[4]中负载扰动表达式如下：

TL=5.133 5+6.498 5sin(ω0t-Asinω0t)

(30)

针对结晶器振动过程中负载转矩的时变特点，仿真研究中在t=2 s时刻突加负载扰动Δd1=10 N·m,且在t=3.5 s时刻突减负载扰动Δd2=10 N·m,用以验证系统的可靠性。

图6～图9所示分别为时变扰动与突加负载变化时，系统在反步控制与PID控制结晶器振动位移跟踪曲线与跟踪误差曲线。由图7可以看出，本文提出方法的误差范围为-0.1～0.1mm，而PID控制方法的误差为0.5mm，故本文采用的方法控制精度较高。由图9可以看出，本文提出的方法与图6相比基本未变化，而PID控制方法的控制精度则有显著较低。由此可知，Backstepping控制较PID控制能够更好地抑制由于负载时变与突变引起的扰动。而经典PID控制方法具有算法简单、控制效果较好等优势，但它在抑制时变与突加负载扰动时，系统的跟踪性能较Backstepping控制方法差，PID控制方法的跟踪误差在负载突变时影响更加明显。

图6 时变无扰动振动位移跟踪曲线Fig.6 Tracking curve of vibration displacement without time-varying load torque disturbances

图7 时变无扰动误差跟踪曲线Fig.7 Tracking error curve of vibration displacement without time-varying load torque disturbances

图8 时变突加扰动振动位移跟踪曲线Fig.8 Tracking curve of vibration displacement with time-varying disturbance

图9 时变突加扰动误差跟踪曲线Fig.9 Tracking error curve of vibration displacement with time-varying disturbance

4 结论

(1)本文研究了结晶器非正弦控制系统中振动位移与伺服电机角位移逆解不唯一问题，提出了一种利用函数映射的方法。

(2)在考虑系统时变负载扰动的情况下，采用了以角位移与伺服电机电流为输入的扩张状态观测器来估计电机转速与负载扰动，并将其补偿到控制器中。

(3)采用Lyapunov定理证明了闭环系统的稳定性，所提出的方法能够实现对时变负载与时变突加负载的自适应控制。

(4)仿真研究表明，映射函数与反步控制相结合的方法符合结晶器非正弦控制系统的性能要求，具备较好的收敛性与鲁棒性。相比于经典PID控制方法，本文所提出的方法不仅实现了对振动位移的精确跟踪控制，而且在突加负载扰动情况下也具有较好的瞬态性能。

[1]ARAKIT,IKEDAM.OptimizationofMoldOscillationforHighSpeedCasting—NewCriteriaforMoldOscillation[J].CanadianMetallurgicalQuarterly,1999,38(5):295-300.

[2]ZHANGXZ,ZHENGXR,LIUQG,etal.InvestigationandApplicationofNon-sinusoidalOscillationTechniqueofMold[J].JournalofIronandSteelResearch,International,2013,20(12):19-24.

[3]MAY,WANGXD,ZANGXY,etal.ExperimentalResearchonEffectofControlModelonLubricationforSlabContinuousCastingMould[J].Iron&SteelMaking,2008,35(3):164-168.

[4]LIXiankui,ZHANGLiping,YANGLadao,etal.DynamicsStudyonNewNon-sinusoidalOscillationSystemofMold[J].JournalofIronandSteelResearchInternational,2008,15(S1):517-522.

[5] 李宪奎. 机械驱动的非正弦振动发生装置: 中国, 专利号CN2395826 [P]. 2000.9.LIXiankui.Non-sinusoidalOscillatingGeneratorDrivenbyMechanism:China,CN2395826 [P].2000.9.

[6] 方一鸣,李宫胤,李建雄,等. 伺服电机驱动连铸结晶器振动系统建模与分析[J]. 仪器仪表学报,2014,35(11):2615-2623.FANGYiming,LIGongyin,LIJianxiong,etal.ModelingandAnalysingforOscillationSystemofContinuousCastingMoldDrivenbyServoMotor[J].ChineseJournalofScientificInstrument,2014,35(11):2615-2623.

[7]ERROUISSIR,OUHROUCHEM,CHENWH,etal.RobustNonlinearPredictiveControllerforPermanent-magnetSynchronousMotorswithanOptimizedCostFunction[J].IEEETransactionsonIndustrialElectronics,2012,59(7):2849-2858.

[8] 黄科元, 周滔滔, 黄守道,等. 含前馈补偿和微分反馈的数控位置伺服系统 [J]. 中国机械工程,2014,25(15):2017-2023.HUANGKeyuan,ZHOUTaotao,HUANGShoudao,etal.CNCPositionServoSystemwithFeedforwardCompensationandDifferentialFeedback[J].ChinaMechanicalEngineering,2014,25(15):2017-2023.

[9] 张兴中, 李宪奎. 连铸结晶器非正弦振动系统模糊神经网络跟踪控制[J]. 中国机械工程,2005,16(2):112-114.ZHANGXingzhong,LIXiankui.FuzzyNeuralNetworkTrackingControlofNon-sinusoidalOscillatioinSystemforContinuousCastingMould[J].ChinaMechanicalEngineering,2005,16(2):112-114.

[10] 马良河,姜建国. 负载转矩未知时变情形下异步电动机的无源性跟踪控制[J]. 电工技术学报,2004,19(1):12-15, 25.MALianghe,JIANGJianguo.InductionMotorTrackingControlBasedonPassivityPrinciplewithUnknownTime-varyingLoadTorque[J].TransactionsofChinaElectrotechnicalSociety,2004,19(1):12-15, 25.

[11] 张晓光,孙力,赵克. 基于负载转矩滑模观测的永磁同步电机滑模控制[J]. 中国电机工程学报,2012,32(3):111-116.ZHANGXiaoguang,SUNLi,ZHAOKe.SlidingModeControlofPMSMBasedonaNovelLoadTorqueSlidingModeObserver[J].JournalofChineseElectricalEngineeringScience,2012,32(3):111-116.

[12] 方一鸣,李智,吴洋羊,等. 基于终端滑模负载观测器的永磁同步电机位置系统反步控制[J]. 电机与控制学报,2014,18(9):105-111.FANGYiming,LIZhi,WUYangyang,etal.BacksteppingControlofPMSMPositionSystemsBasedonTerminal-slidingModeLoadObserver[J].ElectricMachinesandControl,2014,18(9):105-111.

[13] 龙满林, 付永领, 李光华,等. 自抗扰算法在直流力矩电机伺服系统中的应用[J]. 中国机械工程,2012,23(9):1047-1050.LONGManlin,FUYongling,LIGuanghua,etal.ADRAlgorithmAppliedinServoSystemDrivenbyDCTorqueMotor[J].ChinaMechanicalEngineering,2012,23(9):1047-1050.

[14]LIUH,LIS.SpeedControlforPMSMServoSystemUsingPredictiveFunctionalControlandExtendedStateObserver[J].IEEETransactionsonIndustrialElectronics,2012,59(2):1171-1183.

[15] 陈松林,赵海香. 三阶扩张状态观测器的优化参数配置方法[J]. 控制与决策,2014,29(10):1851-1855.CHENSonglin,ZHAOHaixiang.ParameterOptimizationofThird-orderExtendedStateObserver[J].ControlandDecision,2014,29(10):1851-1855.