基于改进人工蜂群算法的机车车辆关键零部件可靠性研究
2018-03-03沈国强贺德强谭文举
沈国强 贺德强 谭文举 苗 剑
1.广西大学机械工程学院,南宁,5300042.南宁轨道交通集团有限责任公司,南宁,530025
0 引言
机车车辆是一个复杂的机电系统,目前我国机车车辆绝大部分采用基于磨损理论的定期检修制度。由于我国对机车车辆可靠性研究工作起步较晚,对车辆零部件寿命分析不足,故有些零部件还处于可靠性较高时期或偶然故障期的较佳状态时便对其进行检修、拆检甚至更换,会造成零部件寿命没能充分得到利用,进而给铁路运营带来较大的经济损失。由此,充分利用机车车辆的历史故障数据对机车车辆的关键零部件进行可靠性分析,有利于提高车辆运行可靠性及运营经济性。
以可靠性为中心的维修(reliability-centered maintenance,RCM)因其先进性和实用性逐渐被认可。王华胜[1]利用相关系数优化法和最小二乘法对机车车辆进行了可靠性分析;王灵芝等[2]对铁路设备关键零部件进行了可靠性分析建模,并用于确定各部件合理的维修时间;刘建强等[3]根据高压系统各部件的可靠性,结合可靠度框图对CRH3动车组的高压系统进行了可靠性研究;周培筠等[4]利用关键零部件可靠性确定客车零部件维修周期;秦金磊等[5]提出了利用单个设备对电站进行以可靠性为中心的检修的研究;刘涛等[6]以民用飞机电动液压泵某部件为例进行了可靠性分析建模,用于确定民机系统部件的维修间隔。以可靠性为中心的维修技术将是机车车辆检修的发展趋势[7]。目前,针对机车车辆可靠性方面的研究较少,对机车关键零部件的研究也相对缺乏,因此,本文提出了一种基于图解法和改进人工蜂群(artificial bee colony,ABC)算法相结合的机车车辆关键零部件可靠性模型拟合方法。首先根据极大似然估计原理建立关于3个参数的似然函数,将求解似然函数的问题转化为求解目标函数的极大值问题。然后利用图解法对参数进行初步估计以获得初始值和ABC算法的搜索空间。再使用ABC算法进行寻优求出3个参数的更优解,从而确定三参数威布尔模型。最后用该模型对机车车辆关键零部件进行可靠性评估,确定机车车辆关键零部件检修间隔,为改进检修策略提供科学的依据。
1 可靠性模型分析
在常见的故障分布中,三参数威布尔分布可称为“万能分布”[8],其他分布如正态分布、指数分布、瑞利分布都可看成是三参数威布尔分布的特例[9],且三参数分布函数的拟合能力较强,因此广泛应用于各种设备的可靠性分析。由于三参数威尔分布模型的具有非线性特征,要确定3个参数极其繁琐,故国内外学者使用基于Gibbs抽样算法、线性回归法、概率加权矩法等不同方法对其进行了研究[9-11],且取得了一定的研究成果。三参数威布尔分布的概率密度函数f(t)、分布函数F(t)及可靠度函数R(t)分别表述为
(1)
(2)
(3)
β,η>0
式中,β为形状参数,决定分布曲线的形状;γ为位置参数(t<γ时表示无故障);η为尺度参数。
由式(1)可得样本的似然函数L为

(4)
对式(4)取自然对数后可得
(5)
根据lnx的单调性可知,L与lnL同时达到最大值,所以当存在L(β′,η′,γ′)使得式(4)成立时,则认为β′、η′、γ′分别为β、η、γ的极大似然函数值。要求(β′,η′,γ′)的解,一般通过求解非线性的超越方程组[12],常规方法求解则极其繁琐,故本文综合图解法和改进ABC算法进行求解。
2 参数求解模型
2.1 图解法
图解法[12]是威布尔三参数估计常用的方法,具有方便、直观、易懂等优点。作图法的缺点是依赖于人的视觉检查,主观意识较强,所得结果比较粗糙。本文利用图解法方便操作的优点,为ABC算法提供解的初值以及搜索空间。
对式(3)进行两次自然对数变换可得
ln(-lnR(t))=βln(t-γ)-βlnη
(6)
令y=ln(-lnR(t)),x=lnt,当t-γ=0,即x=lnγ时,y→-∞;而当t→∞时,y=βx-βlnη。即式(6)经上述变换后可得到x=lnγ和y=βx-βlnη两条渐近线。
三参数威布尔分布利用图解法估计参数的步骤如下:
(1)对于容量为n的样本故障数据,按照从小到大的顺序排列t1 (2)拟合故障数据散点图上的两条渐近线:其中一条与横坐标垂直,位于所有散点的左侧,表达式为x=x0;另一条渐近线表达式为y=kx-b,是x→∞时的渐近线。由式(6)以及两条渐近线的性质可得方程组如下: (7) 求式(7)可得基于图估计的威布尔分布三个参数的估计值分别为γ0=exp(x0),β0=k,η0=exp(b/k)。 2.2.1 算法流程 人工蜂群(ABC)算法是KARABOGA[13]于2005年提出的用于优化多变量函数的函数值算法,该算法已在数值优化、产品拆卸序列规划、工业设计等领域得到了实质应用[14-16]。在ABC算法中,蜂群分为三种:雇佣蜂、跟随蜂、侦查蜂。该算法初始化阶段,将蜂群数量的一半设置为雇佣蜂,且对于每一个蜜源有且仅有一个雇佣蜂,即雇佣蜂的数量等同于蜜源的数量。蜜蜂采蜜的过程就是函数优化过程,获得最优蜜源的过程就是寻找目标函数最优解的过程,ABC算法基本流程可以描述如下: (1)初始化阶段。初始化算法各参数,设置蜂群数量一半为雇佣蜂,雇佣蜂根据下式初始化蜜源并记录最优蜜源: Xij=lb(j)+r(ub(j)-lb(j)) (8) 式中,i的取值范围为1到蜂群数量的50%;j为蜜源位置的第j个参数;lb(j)和ub(j)分别为参数Xij的最小值和最大值;r为(0,1)的随机数。 (2)雇佣蜂更新蜜源阶段。雇佣蜂在蜜源附近利用下式进行邻域搜索: Vkj=Xij+Rij(Xij-Xkj) -1≤Rij≤1 (9) 式中,Vkj为新蜜源;Xkj为随机的不同于Xij的临近蜜源;Rij为一个随机参数。 并计算相应的函数目标值,然后通过贪婪选择来选择新旧蜜源中更优的蜜源。 (3)跟随蜂选择蜜源阶段。跟随蜂根据雇佣蜂分享的蜜源信息进行蜜源选择,通过下式计算蜜源被选择的概率Pi,概率越大则被选择的可能性越大: (10) 式中,f(θi)为第i个蜜源的适应值。 在最小化问题中,f(θi)可由下式求得: (11) 式中,fi为根据蜜源计算的目标函数值。 (4)侦查蜂阶段。判断当前试验次数Nt是否超过设定数值极限Nlim,如果超过,则放弃当前蜜源,相应的雇佣蜂转为侦查蜂,通过式(8)重新搜索新的蜜源。最后判断算法循环次数,若小于设定的最大值cmax,则算法循环;反之,则输出最优蜜源,算法结束,以获得目标函数最优解。 2.2.2 改进的人工蜂群算法 标准ABC算法中雇佣蜂更新蜜源阶段采用的是式(9)搜索新蜜源,通过随机参数Rij控制邻域搜索区间,但易使算法陷入局部最优且算法速度较慢的局面,故本文采用合适的比例因子δij确定搜索区间[16],比例因子及新的搜索公式如下: (12) 式中,μ1,μ2为两个随机因子。 Vkj=Xij+δij(Xij-Xkj) (13) 在改进算法中,根据式(9)进行蜜源位置更新,比例因子随着试验次数Nt的变化而进行改变。 (1)更新蜜源初始阶段。比例因子δij和搜索邻域足够大,故算法对新蜜源的选择性更好,从而使算法跳出局部最优;但试验次数达到一定程度后,δij较小,缩小了搜索邻域,进而提高了后期搜索效率。 (2)跟随蜂选择蜜源阶段。标准ABC算法中,蜜源被选择的概率根据式(10)计算得到,且Pi越大,相对应的蜜源被跟随蜂选择的概率越大,在选择过程中,可能会出现一些竞争力太突出的超常个体,这些个体会掌控选择过程会影响算法全局搜索能力,导致算法陷入局部最优;反之,如果各蜜源的适应度相差不大,则容易忽略优秀个体,对算法的收敛速度会有一定程度的影响,进而增加运算时间。本文算法中,跟随蜂依照下式选择蜜源: (14) 式中,fi为第i个蜜源的适应度值;mf为全部蜜源中的最大适应度值;c为循环次数。 在算法前期,增大蜜源被选择的概率,防止出现因个别超常个体而陷入局部最优的局面;在算法后期,倾向于选择更优的蜜源,从而能更快的获得最优蜜源。 改进ABC算法是全局寻优算法,并且有算法简单、易于实现、鲁棒性强、全局寻优能力明显等优点,因此适用于三参数威布尔函数的优化,其算法流程如图1所示。 图1 改进人工蜂群算法流程图Fig.1 Flow chart of improved ABC algorithm 2.2.3 ABC算法搜索空间 蜜蜂在蜂巢附近搜索蜜源必须有一定的搜索空间,对于三参数威布尔函数,蜜源位置由威布尔的3个参数所确定,故其搜索空间也是由3个参数组成的空间所确定。本文中搜索空间由图解法所解得的初始值(β0,η0,γ0)和宽松系数θ(0<θ<1)所确定,参数的搜索空间为 (15) 2.2.4 分布拟合优度评估 根据故障数据初步选定的分布类型需要进行检验,拟合优度检验是一种常用的分布检验方法。拟合优度是衡量选定的分布与故障数据实际分布之间的符合程度的度量。本文使用S-K检验对三参数威布尔分布进行检验。S-K检验是一种常见的拟合优度检验,S-K检验首先将n个故障数据按从小到大进行排列,然后分别计算每个故障数据的三参数威布尔分布函数R0(ti),并将其与经验分布函数Rn(ti)(本文采用秩法)进行比较,通过下式计算获得两者差值的绝对值即S-K检验统计量Dn: Dn=sup|Rn(ti)-R0(ti)|=max(δi) (16) Rn(ti)=(i-3)/(n+4) 下面以文献[2]某型减振器的12个样本故障数据进行计算,其寿命数据为20.0,23.5,24.0,27.5,30.5,35.5,38.0,41.0,50.5,52.0,68.0,77.0。现分别采用最小二乘法[2]和文中提出的改进ABC算法对上述样本进行三参数威布尔函数参数估计,计算结果见表1。 表1 参数估计值比较(与最小二乘法比较)Tab.1 Comparison of parameter estimation values (compared with the least squares method) 由表1可以看出,运用改进ABC算法进行计算的似然函数值大于最小二乘法所得的似然函数值,说明改进ABC算法的计算精度高于最小二乘法的相关系数法和相结合的计算方法。 以文献[11]中利用蒙特卡罗模拟产生的数据为例进行分析,其故障数据见表2。 表2 蒙特卡罗模拟样本数据Tab.2 Data of Monte Carlo simulation sample 图2 蒙特卡罗模拟样本数据威布尔概率图及渐近线图Fig.2 Weibull probability plots and asymptote graph of data of Monte Carlo simulation sample 图2为使用图解法求得的故障样本的散点图。由图2可以看出,各散点存在明显的拐点,并不是全在同一直线上,样本符合三参数威布尔分布特征,所以可以假设样本分布服从三参数威布尔分布。在图上作散点图的渐近线,其表达式分别为 (17) 从而可解得图解法解三参数威布尔分布的参数初始解为β=3.93,η=47.8,γ=32.46。 为了得到更优解,可以扩大ABC算法的搜索空间,令宽松系数θ=0.7,可以得到参数搜索范围为 运用人工蜂群算法进行计算,得到的参数估计目标函数的最大似然估计值见表3。由表3可以看出,相对于文献[11]的概率加权矩法,改进ABC算法估计的参数具有更好的最大似然估计值,所得的估计参数更加精准。图3所示为优化迭代结果。 表3 参数估计值比较(与概率加权矩法比较) 图3 优化迭代结果Fig.3 The iterative result of optimization 某车辆制动系统闸片的寿命样本数据见表4。根据图解法计算步骤,闸片寿命时间散点图见图4。由图4可知,选定此车辆闸片的寿命时间服从三参数威布尔分布。求出渐近线表达式如下: (18) 即图解法的初始解为β=3.55,η=89 321.72,γ=36 315.5。 令θ=0.7,可得到ABC算法参数搜索范围为 运用改进ABC算法进行优化求解,得:β=3.059,η=74 880.3,γ=18 952.6,极大似然函数为-334.228,S-K检验统计量为 Dn=0.057 所以闸片的寿命时间符合三参数威布尔分布。 根据式(3)可得该闸片的寿命时间可靠度函数为 表4 某机车闸片寿命数据 R(t)=e-[(t-18 952.6)/74 880.3]3.059 (19) 图4 某机车制定闸片寿命数据威布尔概率图及渐近线图Fig.4 Weibull probability plots and asymptotic graph of brake pad life data of locomotive 根据函数利用MATLAB仿真,得到闸片的可靠度曲线如图5所示。由图5可以看出,均匀分布在可靠度曲线两侧的散点是闸片寿命时间点的经验分布函数值,且三参数威布尔分布与文中所给的参数估计方法都适用于闸片的寿命分析。因此决策人员可根据机车实际运营中具体的可靠度要求,利用可靠度计算公式得到制动系统闸片合理的检修周期。 图5 机车车辆制定闸片寿命数据可靠度函数图Fig.5 Reliability graph of brake pad life of locomotive (1)采用三参数威布尔模型分析机车车辆关键零部件以可靠性为中心的检修时,针对其参数估计的复杂性,将参数估计转化为求似然函数极大值问题。然后,根据图解法给出参数的初值以及ABC算法的搜索空间,再利用改进ABC算法进行迭代求解,得出威布尔分布参数的参数估计值。本方法具有计算简单、参数估计精度高的优点。 (2)以制动系统闸片为例,通过计算其可靠性指标,确定系统维修的最佳维修周期。可将本模型应用到机车车辆其他关键零部件,如转向架、轮对等的可靠性评估,从而确定零件检修的最佳维修周期,为机车车辆检修规程的改进提供科学依据。 [1] 王华胜. 基于加权最小二乘法的机车车辆零部件可靠性分析[J]. 铁道学报,2001,23(6):21-25.WANGHuasheng.ReliabilityAnalysisofLocomotiveandCarPartsBasedonWeightedLeastSquareMethod[J].JournaloftheChinaRailwaySociety,2001,23(6):21-25. [2] 王灵芝, 徐宇工, 张家栋. 铁路设备关键零部件的可靠性分析模型及其应用研究[J]. 铁道学报,2008,30(4):93-97.WANGLingzhi,XUYugong,ZHANGJiadong.ResearchonReliabilityAnalysisModelforKeyComponentsandPartsofRailwayEquipmentandItsApplication[J].JournaloftheChinaRailwaySociety,2008,30(4):93-97. [3] 刘建强, 崔秀国, 孙帮成, 等.CRH3型动车组高压电器系统可靠性研究[J]. 铁道学报,2013,35(6):22-27.LIUJianqiang,CUIXiuguo,SUNBangcheng,etal.ResearchonReliabilityofHighVoltageApparatusSystemofCHR3ElectricMultipleUnits[J].JournaloftheChinaRailwaySociety,2013,35(6):22-27. [4] 周培筠, 宋永增, 曾德锋. 用可靠性方法计算客车关键零部件维修周期[J]. 铁道机车车辆,2006,26(3):42-44.ZHOUPeiyun,SONGYongzeng,ZHENGDefeng.DeterminingOptimumMaintenancePeriodforTrain`sKey-partswiththeReliabilityTheory[J].RailwayLocomotive&Car,2006,26(3):42-44. [5] 秦金磊, 牛玉广, 李整. 电站设备可靠性问题的威布尔模型求解优化方法[J]. 中国电机工程学报,2012,32(增刊1):35-40.QINJinlei,NIUYuguang,LIZheng.OptimizationApproachofWeibullModelSolutionforPowerStationEquipmentReliability[J].ProceedingsofCSEE,2012,32(S1):35-40. [6] 刘涛, 苏茂根. 民机系统部件维修间隔的确定方法研究[J]. 机械工程与自动化,2015(3):139-140,144.LIUTao,SUMaogen.DeterminingMaintenanceTaskIntervalofCivilAircraftSystemComponent[J].MechanicalEngineering&Automation,2015(3):139-140,144. [7] 狄威. 简论机车车辆的可靠性与维修性及维修信息管理[J]. 北京交通大学学报,2007,31(6):15-17,21.DIWei.ReliabilityMaintainabilityandMaintenanceInformationManagementofLocomotiveandCar[J].JournalofBeijingJiaotongUniversity,2007,31(6):15-17,21. [8]MURTHYDNP,BULMERM,ECCLESTONJA.WeibullModelSelectionforReliabilityModelling[J].ReliabilityEngineering&SystemSafety,2004,86(3):257-267. [9] 刘飞, 王祖尧, 窦毅芳, 等. 基于Gibbs抽样算法的三参数威布尔分布Bayes估计[J]. 机械强度,2007,29(3):429-432.LIUFei,WANGZuyao,DOUYifang,etal.BayesianAnalysisofThree-parameterWeibullDistributionBasedonGibbsSamplingAlgorithm[J].JournalofMechanicalStrength,2007,29(3):429-432. [10]HUDAKD,TIRYAKIOGLUM.OnEstimatingPrcentilesoftheWeibullDistributionbytheLinearRegressionMethod[J].JournalofMaterialsScience,2009,44(8):1959-1964. [11] 邓建, 古德生, 李夕兵. 确定可靠性分析Weibull分布参数的概率加权矩法[J]. 计算力学学报,2004,21(5):609-613.DENGJian,GUDesheng,LIXibing.ParametersandQuantileEstimationforFatigueLifeDistributionUsingProbabilityWeightedMoments[J].ChineseJournalofComputationalMechanics,2004,21(5):609-613. [12] 杨谋存, 聂宏. 三参数Weibull分布参数的极大似然估计数值解法[J]. 南京航空航天大学学报,2007,39(1):22-25.YANGMoucun,NIEHong.AdvancedAlgorithmforMaximumLikelihoodEstimationofThreeParameterWeibullDistribution[J].JournalofNanjingUniversityofAeronautics&Astronautics,2007,39(1):22-25. [13]KARABOGAD.AnIdeaBasedonHoneyBeeSwarmforNumericalOptimization[R].Kayseri:ErciyesUniversity,2005. [14]KARABOGAD,BASTURKB.APowerfulandEfficientAlgorithmforNumericalFunctionOptimization:ArtificialBeeColony(ABC)Algorithm[J].JournalofGlobalOptimization,2007,39(3):459-471. [15] 宋守许, 张文胜, 张雷. 基于改进人工蜂群算法的产品拆卸序列规划[J]. 中国机械工程,2016,27(17):2384-2390.SONGShouxu,ZHANGWensheng,ZHANGLei.ProductDisassemblySequencePlanningBasedonImprovedArtificialBeeColonyAlgorithm[J].ChinaMechanicalEngineering,2016,27(17):2384-2390. [16] 何鹏, 阎兴頔, 侍洪波. 一种快速自适应蜂群算法及其应用[J]. 华东理工大学学报(自然科学版),2013,39(5):588-595.HEPeng,YANXingdi,SHIHongbo.AQuickSelf-AdaptiveArtificialBeeColonyAlgorithmandItsApplication[J].JournalofEastChinaUniversityofScienceandTechnology(NaturalScienceEdition), 2013,39(5):588-595.2.2 人工蜂群算法模型


3 实例分析
3.1 机车车辆某型减振器可靠性分析

3.2 蒙特卡罗模拟分析比较
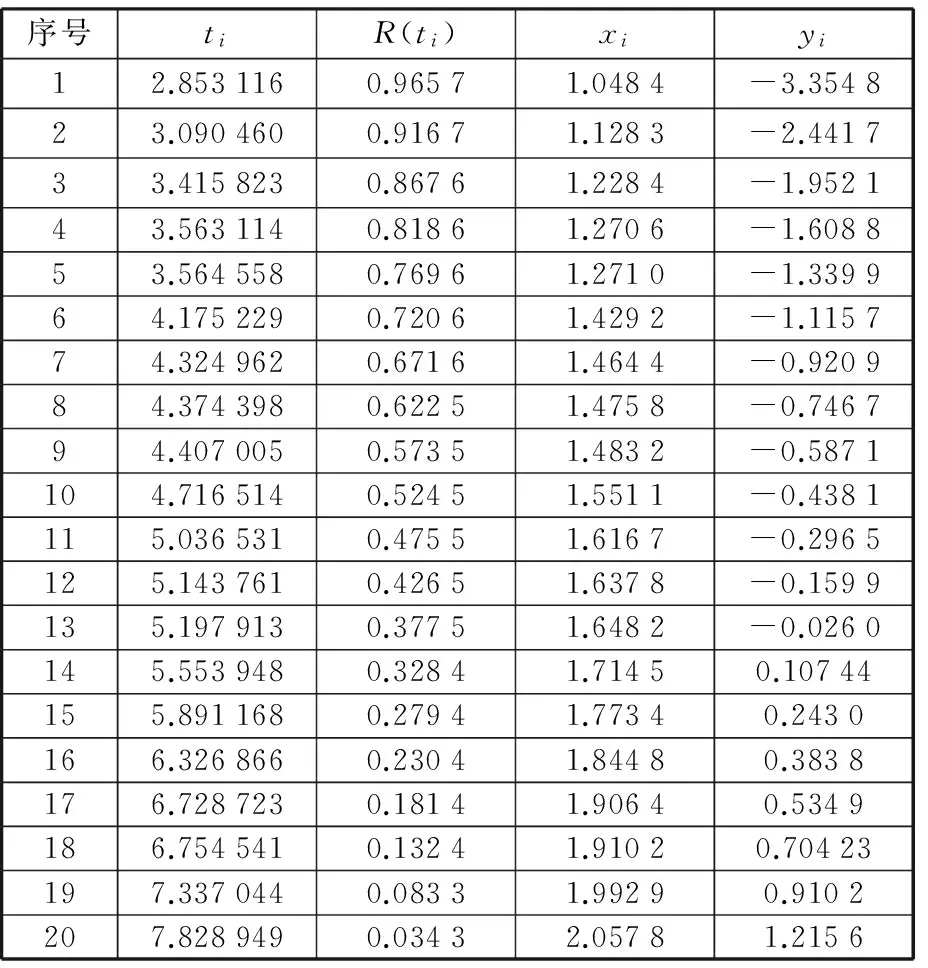




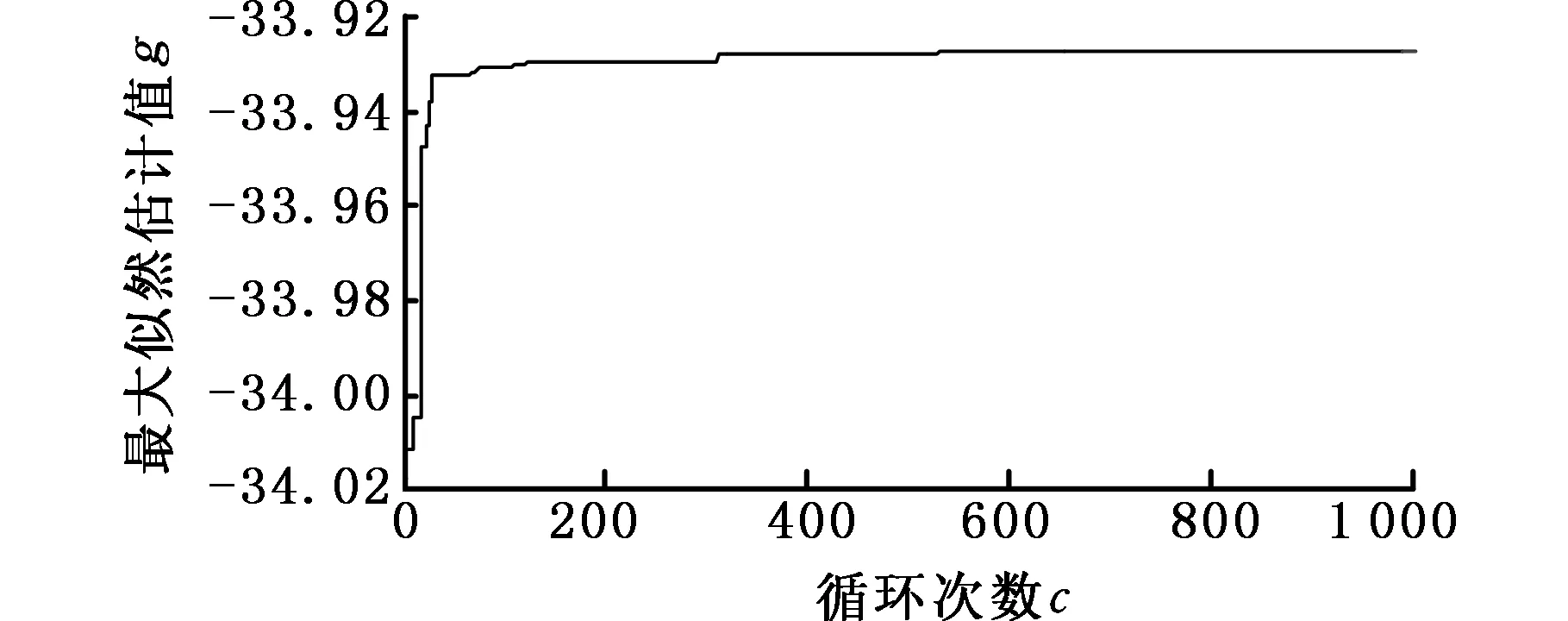
4 可靠性模型应用





5 结论
