谱极值图论的最新进展和相关问题
2018-03-01陈明珠张晓东
陈明珠,张晓东
(上海交通大学 数学科学学院,教育部科学工程计算重点实验室,上海 200240)
论文系统介绍谱极值图论的最新研究成果、进展以及相关问题.主要内容含有各种Turán类型,包括完全子图、线性森林、圈、二部图以及图子式等邻接谱和无符号拉普拉斯谱的最新研究成果,同时介绍该领域的尚未解决的猜想和相关问题.
Turán类型问题;禁用子图;谱半径;无符号拉普拉斯谱半径
论文考虑的图都是有限无向简单图.令G=(V(G),E(G))是一个简单图,其中V(G)为顶点集,E(G)为边集.用e(G)表示图G的边数.给定两个点无交的简单图G和H,G∪H表示G和H的不交并.kG表示k个同构图G的不交并,G∨H表示由G∪H通过添加所有的连接G中的点和H中的点的边而得到的图.线性森林指的是几条不交路的并.如果一个图H能从图G中通过删边、收缩边或者删点得到,那么称H是图G的H-子式,反之,称图G不含H-子式.
图G的邻接矩阵A(G)是n×n矩阵(aij), 如果vi和vj邻接,则aij=1, 否则为0.图G的无符号拉普拉斯矩阵Q(G)是n×n矩阵(qij), 其中对角元素qii为顶点i的度,对于非对角元素,如果vi和vj邻接,则qij=1, 否则为0.易知,图G的邻接矩阵A(G)和无符号拉普拉斯矩阵Q(G)的特征值都是实数.图G的谱半径就是它的邻接矩阵A(G)的最大特征值,记为ρ(G).图G的无符号拉普拉斯谱半径就是它的无符号拉普拉斯矩阵Q(G)的最大特征值,记为q(G).
1 Turán类型极值图论问题
谱极值图论问题主要研究与图相伴随的各种矩阵,包括邻接矩阵、拉普拉斯矩阵或无符号拉普拉斯矩阵等的谱性质,特别是关于不含有特殊子结构的图类中谱半径或者其他特征值和特征向量,例如Stanley界[4]和Wilf定理[5].其中最典型的就是Nikiforov[6]在2010年提出的谱Turán类型极值问题:求不包含给定的图H作为子图的所有n个顶点的图的最大谱半径.稍作变形,可得另外一个典型的谱Turán类型极值问题:求不包含给定的图H作为子图的所有n个顶点的图的最大无符号拉普拉斯谱半径.很多典型的Turán类型极值问题的谱版本也成立.
论文主要介绍的是谱Turán类型极值问题的一些主要最新研究结果、最新进展以及相关问题和猜想.全文安排如下:第二部分介绍谱Turán定理(禁用完全子图);第三部分介绍禁用线性森林的谱Turán类型极值问题;第四部分介绍禁用圈的谱Turán类型极值问题;第五部分介绍禁用完全二部图的谱Turán类型极值问题,也就是Zarankiewicz谱Turán类型极值问题;第六部分介绍禁用图子式的谱Turán类型极值问题.
2 谱Turán定理
2.1 邻接谱Turán定理
Wilf[5]在1986年利用图的顶点数和团数,给出了图的谱半径的上界.
定理1[5]令G是一个顶点数为n的简单图.若G的团数为ω(G)=ω, 则
ρ(G)≤(1-1/w)n.
令函数f(x)=(1-1/x)n(其中n为正常数).当x>0时,f是增函数,则定理1等价于定理2.
定理2 令G是一个顶点数为n的简单图.若G不含Kr+1作为子图,则
ρ(G)≤(1-1/r)n.
然而,只有r整除n的时候,定理2中不等式的等号才能成立.因此定理2中的界不是最优的.实际上,Nikiforv[7]在2007年改进了定理2,得到了谱Turán定理.Guiduli[8]也证明了相同的结果.
定理3[7-8]令G是一个顶点数为n的简单图.若G不含Kr+1作为子图,则
ρ(G)≤ρ(Tn,r),
等号成立当且仅当G=Tn,r.
实际上,定理3也改进了定理1,它等价于定理4.
定理4 令G是一个顶点数为n的简单图.若G的团数为ω(G)=ω, 则
ρ(G)≤ρ(Tn,ω),
等号成立当且仅当G=Tn,ω.
利用不等式ρ(G)≥2e(G)/n, 定理3可以推出经典的Turán定理.
推论1[3]令G是一个顶点数为n的简单图.若G不含Kr+1作为子图,则
e(G)≤e(Tn,r),
等号成立当且仅当G=Tn,r.
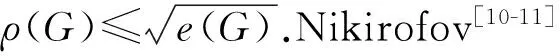
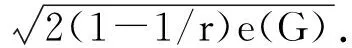
若G没有孤立点,则等号成立当且仅当下列两种情况之一成立:
(i) r=2而且G是完全二部图;
(ii) r≥3而且G是正则完全r-部图.
实际上,Nikiforov[10-11]还得到了下列推论,证明Edward等[13]在1983年提出的猜想即推论2.
推论2[10]令G是一个顶点数为n的简单图.若G的团数为ω(G)=ω, 则
若G没有孤立点,则等号成立当且仅当下列两种情况之一成立:
(i)ω=2而且G是完全二部图;
(ii)ω≥3而且G是正则完全ω-部图.
定理6[11]令G是一个顶点数为n的简单图.若G的团数为ω(G)=ω, 则
若G没有孤立点,k≥1, 则等号成立,则
(i) 若k=1,则G是正则完全ω-部图;
(ii) 若k≥2和ω>2, 则G是正则完全ω-部图;
(iii) 若k≥2和ω=2, 则G是完全二部图.若k是奇数,则G是正则完全二部图.
2.2 谱半径和独立数
ρ(G)≥n/α-1.
实际上,谱半径和独立数满足下列更精确的结果如下:
定理7[14]令G是一个顶点数为n的简单图.若G的独立数为α, 则
从资金规模来看,2017年,全国创投管理资本总量达到8 872.5亿元,较2016年增加595.4亿元,增幅为7.2%,较前两年明显放缓(见图2)。此外,基金两极分化的“杠铃”现象进一步显现② 两极分化现象是各国发展的共同特征,如2017年美国创投统计数据显示,管理资金超过10亿美元的机构数量,从2016年的68家增加到83家,占比8.6%;管理资金小于2 500万美元的机构数量,从2016年的241家增加到2017年的427家,占当年比重的44%。,管理资本规模超过5亿元的机构虽然仅占10.2%,但掌握了72.1%的管理资本总量。


定理8[16]令G是一个独立数为α的顶点数为n=kα的简单连通图.若α=3,4, 则
ρ(G)≥ρ(Pn,α),
其中:图Pn,α是把一条长为α-1的路中每个顶点被k的团取代并且有2α-2个割点所得到的简单图.
最近Jin等[17]进一步考虑一般情形,并且推广他们的结果.
定理9[17]令G是一个独立数为α的顶点数为n=kα的简单连通图.若k>(17α+15)/8, 则
ρ(G)≥ρ(Pn,α),
其中:图Pn,α是把一条长为α-1的路中每个顶点被k的团取代并且有2α-2个割点所得到的简单图,等号成立当且仅当G是Pn,α.
显然上面定理并没有完全刻画独立数为α的n个顶点的简单连通图中具有最小谱半径的所有极图,这是一个非常有趣的问题.
2.3 无符号拉普拉斯谱Turán定理
Abreu等[18]在2013年研究给定顶点数和团数的简单图的无符号拉普拉斯谱半径,证明了Hansen等[19]在2009年提出的猜想.
定理10[18]令G是一个顶点数为n的简单图.若G的团数为ω(G)=ω, 则
q(G)≤2(1-1/w)n.
类似于定理1等价于定理2,定理10也等价于以下定理:
定理11 令G是一个顶点数为n的简单图.若G不含Kr+1作为子图,则
q(G)≤2(1-1/r)n.
He等[20]在2013年也研究给定顶点数和团数的简单图,给出了这类图的无符号拉普拉斯谱半径的紧的上界,并刻画了极图.
定理12[20]令G是一个顶点数为n的简单图.若G的团数为ω(G)=ω≥2, 则
其中:n=kω+s, 0≤s<ω.
另外,等号成立当且仅当下面情况之一成立:
(i)ω=2且G是完全二部图;
(ii)ω≥3,G=Tn,ω.
定理12等价于定理13.
定理13[20]令r≥2和G是一个顶点数为n的简单图.若G不含Kr+1作为子图,则
其中:n=kr+s, 0≤s 另外,等号成立当且仅当下面情况之一成立: (i)r=2且G是完全二部图; (ii)r≥3且G=Tn,r. 利用不等式q(G)≥4e(G)/n, 定理13可以推出经典的Turán定理. 推论3[3]令r≥3和G是一个顶点数为n的简单图.若G不含Kr+1作为子图,则 e(G)≤e(Tn,r), 等号成立当且仅当G=Tn,r. 若r≥3, 定理3、13的极图是一致的.但是当r=2, 定理3的极图是唯一的,而定理13的极图却不是唯一的.这是因为完全二部图的无符号拉普拉斯谱半径就是它的顶点数.这说明邻接谱极图和无符号拉普拉斯谱极图并不定是完全一致的. Erdös等[21]在1959年给出了不含给定长度的路作为子图的简单图的最大边数. 定理14[21]令h≥2和G是一个顶点数为n的简单图.若G不含Ph作为子图,则 e(G)≤(h-2)n/2, 等号成立当且仅当G是顶点数为h-1的完全图的不交并. 注意到若Erdös-Gallai定理[21]中的等号成立,则h-1整除n, 也就是说若h-1不能整除n, Erdös-Gallai定理还不是最优的.他们的结果已陆续得到改进,如定理15. 定理15[22]令h≥1和G是一个顶点数为n>(5h+4)/2的简单连通图,则 (1) 若G不含P2h+2作为子图,则e(G)≤e(Sn,h),等号成立当且仅当G=Sn,h; Erdös-Gallai[21]定理,即如果简单图G的平均度超过h-2, 则G包含Ph作为子图.下列著名的Erdös-Sós猜想[23]是Erdös-Gallai定理[21]的推广. 猜想1[23]令h≥2.如果简单图G的平均度超过h-2, 则G包含所有顶点数为h的树作为子图. Erdös-Sós猜想自提出以来一直受到很大的关注.对于很多给定的特殊的树类,特别是直径最多为4的树[24],其对应的Erdös-Sós猜想已经被证明是正确的.关于该方面的进展可以参考文[25-26]以及后面的参考文献.近年,Ajtai等利用正则引理给出了对于k充分大的Erdös-Sós猜想的证明. 线性森林是几条路的不交并.对于l≥3和顶点数n充分大,Bushaw等[27]给出了不含kPl作为子图的简单图的最大边数,并刻画了极图.Lidick等[28]把 Bushaw-Kettle结果拓展到了任意的顶点数充分大的线性森林. (i) 若k≥1, 则e(G)≤e(Sn,h), 等号成立当且仅当G=Sn,h; 关于F=lP3, Yuan等[29]刻画了对应所有极图. 定理17[29]令F=lP3和G是一个顶点数为n的简单图.若G不含F作为子图,则 (i) 当n<3k时,e(G)≤n(n-1)/2; 并且刻画了所有的极图. 类似于谱Turán定理,自然会问如果定理15的边数换为谱半径,结论是否成立? 实际上,Nikiforov[6]在2010年给出了肯定的答案. 定理18[6]令h≥1和G是一个顶点数为n≥24h的简单图,则 (i) 若G不含P2h+2作为子图,则ρ(G)≤ρ(Sn,h),等号成立当且仅当G=Sn,h; 另外, Zhai等[30]研究不含给定长度的路作为子图的二部图,并给出了最大谱半径和刻画了极图. 根据著名的Erdös-Sós猜想[23],Nikiforov[6]提出了比定理18更为一般化猜想,即猜想2. 猜想2[6]令h≥2和G是一个顶点数为n充分大的简单图,则 (1) 若G不含某顶点数为2h+2的树作为子图,则ρ(G)≤ρ(Sn,h),等号成立当且仅当G=Sn,h; 定理18实际上证明了猜想2中的树为路的情况. 回到线性森林的问题上,指出定理16对应的谱半径版本也成立,而它的证明几乎可以把定理18的证明移植过来. (i) 若k≥1, 则ρ(G)≤ρ(Sn,h), 等号成立当且仅当G=Sn,h; 在前一小节,定理15的边数换为谱半径,结论仍然成立,那么定理15的边数换为无符号拉普拉斯谱半径,结论是否仍然成立? Yuan等[31]在2014年也给出了肯定的回答. 定理20[31]令h≥1和G是一个顶点数为n≥7h2的简单图,则 (i) 若G不含P2h+2作为子图,则q(G)≤q(Sn,h),等号成立当且仅当G=Sn,h; 记Mh是一个h-匹配,即Mh是由h条匹配边组成的.易知Mh是最简单的线性森林.Yu[32]证明了禁用(h+1)-匹配的结果,即定理21. 定理21[32]令h≥1和G是一个顶点数为n的简单图.若G不包含Mh+1作为子图,则 (iii) 若n>(5h+3)/2, 则q(G)≤4h,等号成立当且仅当G=Sn,h. (i) 若h=1且n≥8 则q(G)≤q(F2,2(n)), 并且等号成立当且仅当G=F2,2(n); 4.1.1 禁用奇圈 定理24中的常数n/320毫无疑问不是最优的,但是最优值还是个未知数. 结合定理24,易见不含奇圈作为子图的简单图的紧的谱上界. 推论4[33]令h≥1且n>320(2h+1).若G是一个顶点数为n且不含C2h+1作为子图的简单图,则 4.1.2 禁用C4 Nikiforov[7]在2007年给出不含C4作为子图的简单图的谱半径上界,并刻画了极图. 定理25[7]令G是一个顶点数为n的简单图,谱半径为ρ.若G不含C4作为子图,则ρ2-ρ-(n-1)≤0, 等号成立当且仅当G中的任意两个顶点有且只有一个公共邻点,也就是说G是友谊图(G=K1∨(n-1/2)K2). 易知,使得定理25等号成立的n必然是奇数,即如果n是偶数,定理25还可以被改进. 注意到Fs,t(n)=Ks-1∨(pKt∪Kl), 其中n-s+1=pt+l, 0≤l 定理26[39]令G是一个顶点数为n的简单图,谱半径为ρ.若G不含C4作为子图,则ρ3-ρ2-(n-1)ρ+1≤0, 等号成立当且仅当G=F2,2(n). 极值图论中很多经典结果[34]在谱极值图论中都有相对应的谱结果,除了前面几节介绍的,还有Matel定理在谱极值图论对应: (定理2)若ρ(G)>ρ(T2(n)), 则G包含三角形作为子图; Bollabás结果在谱极值图论对应:(定理24)若ρ(G)>ρ(T2(n)), 则对每个t≤n/320,G都包含了一个长度为t的圈. Nikiforov[42]还刻画了定理27等号成立的条件,但是由于证明比较复杂,省去了证明. 4.1.3 禁用长度至少为6的偶圈 定理25能够对任意的偶圈一般化为:若h≥1且G不含C2h+2作为子图,则 实际上,Nikiforov[6]证明了更强的结果,即定理29. 定理29[6]令h≥1,1≤l≤h, 和G是一个顶点数为n的简单图.若G不含某个C2l+2作为子图,则 Nikiforov[6]定义f2h+2(n):=max{ρ(G):G是一个顶点数为n且不含C2h+2作为子图的简单图}. 定理29意味着 Nikiforov[6]提出了猜想3. 定理30[43]令h≥2和G是一个顶点数为n充分大的简单图.若G不含任意一个长度至少为2h+2的圈作为子图,则 注意到若n≥2h+3, G不含P2h+3作为子图,则G必不含任意一个长度至少为2h+2的圈作为子图.定理30蕴含了定理18(ii). 4.1.4 禁用圈对{Cl,Cl+1} Nikiforov[6]定义gl(n):=max{ρ(G):G是一个顶点数为n且不含Cl和Cl+1作为子图的简单图}. 对于l≥3,gl(n)的具体值应该多少呢? Nikiforov[6]证明了渐进定理,即定理31. 定理31[6]令h≥1和G是一个顶点数为n的简单图.若G既不含C2h+1也不含C2h+2作为子图,则 同时,Nikiforov[6]给出了既不含C2h+1也不含C2h+2作为子图的简单图的谱极图猜想,即猜想4. 猜想4[6]令h≥2和G是一个顶点数为n的简单图.若G既不含C2h+1也不含C2h+2作为子图,则 ρ(G)≤ρ(Sn,h), 等号成立当且仅当G=Sn,h. Yuan等[45]首先证明h=2时猜想4是正确的.最近,Gao等[43]证明了比猜想4弱的结论,即定理32. 定理32[43]令h≥2和G是一个顶点数为n≥13h2的简单图.若G不含任意一个长度至少为2h+1的圈作为子图,则 ρ(G)≤ρ(Sn,h), 等号成立当且仅当G=Sn,h. 注意到若n≥2h+2,G不含P2h+2作为子图,则G必不含任意一个长度至少为2h+1的圈作为子图.定理32蕴含了定理18(i). 对于偶圈,q(G)和ρ(G)有类似的结果.de Freitas等[46]首先证明关于C4的相关结果. 定理33[46]令G是一个顶点数为n≥4的简单图.若G不含C4作为子图,则 q(G)≤q(F2,2(n)), 等号成立当且仅当G=F2,2(n). 同时,他们也提出了关于偶圈的更一般猜想,而这猜想最后在2015年被Nikiforov等[47]解决了. 定理34[47]令h≥2和G是一个顶点数为n≥400h2的简单图.若G不含C2h+2作为子图,则 对于奇圈,q(G)和ρ(G)结果是不一致的.当n充分大,不含C2h+1作为子图的简单图满足ρ(G)≤ρ(T2(n)), 但是对于q(G), de Freitas等[46]首先证明C5的相关结果. 定理35[46]令G是一个顶点数为n≥6的简单图.若G不含C5作为子图,则 ρ(G)≤ρ(Sn,2), 等号成立当且仅当G=Sn,2. 同时,他们也提出了关于奇圈的更一般猜想,即猜想5. 猜想5[46]令h≥2和G是一个顶点数为n充分大的简单图.若G不含C2h+1作为子图,则 q(G)≤q(Sn.h), 等号成立当且仅当G=Sn,h. Nikiforov[48]在2014年渐进解决了猜想5. 定理36[48]令h≥2和G是一个顶点数为n>5h2的简单图.若q(G)≥n+2h-2,则G包含C2h+1和C2h+2作为子图. 后来,猜想5在2015年被Yuan[49]解决了. 定理37[49]令h≥3和G是一个顶点数为n≥110h2的简单图.若G不含C2h+1作为子图,则 q(G)≤q(Sn.h), 等号成立当且仅当G=Sn,h. 在极值图论中著名的Zarankiewicz问题[50]为:不含Ks,t作为子图的简单图的最大边数是多少? Zarankiewicz问题的谱版本: 不含Ks,t作为子图的简单图的最大谱半径或者最大无符号拉普拉斯谱半径是多少?除了一些特殊情况,这类问题并没有得到完全解决. Babai等[51]证明了不含Ks,t作为子图的简单图的谱半径的上界. ρ(G)≤((s-1)1/t+o(1))n1-1/t. Nikiforov[52]使用不同方法改进了他们的结果,即定理38. 定理38[52]令s≥t≥2和G是一个顶点数为n的简单图.若G不含Ks,t作为子图,则 (ii) 若t≥3 则ρ(G)≤(s-t+1)1/tn1-1/t+(t-1)n1-2/t+t-2. 由于ρ(G)≥2e(G)/n, 定理38蕴含推论5. 推论5[52]令s≥t≥2和G是一个顶点数为n的简单图.若G不含Ks,t作为子图,则 (ii) 若t≥3 则ρ(G)≤(1/2)(s-t+1)1/tn2-1/t+(1/2)(t-1)n2-2/t+(t-2)n/2. 这个结果改进了Füredi[53]的结果. 对于s=t=2, G不含K2,2作为子图,有 定理25意味着定理38(i)的界是紧的,而且等号成立当且仅当G是友谊图. 另外,Erdös等[41]证明:如果q是素数幂,极性图(polaritygraph)ERq不含K2,2作为子图,易见ERq的顶点数为n=q2+q+1和e(ERq)=q(q+1)2/2.因此 这个界非常接近定理38(i)的上界.但是这个界并不是对所有的n都是紧的,所以它还不是最优的. 对于s≥3, t=2, 定理38(i)是紧的,此时G可以是任意两个顶点都有且只有s-1个公共邻点的强正则图. 对于s=t=3, 定理38(i)意味着:若G不含K3,3作为子图,顶点数为n, 则 ρ(G)≤n2/3+2n1/3+1. ρ(G)≥n2/3+(2/3)n1/3+C, 其中:C>0是某个常数.因此,定理38(ii)的界是渐进紧的. 若加入最大度参数,Shi等[55]得到了定理39. 定理39[55]令t≥2和G是一个顶点数为n的简单连通图.若G不含K2,t作为子图且最大度为Δ, 则 等号成立当且仅当G是(n,Δ,t-1,t-1)-强连通图. 不像一般的Turán类型极值问题(禁用非二部子图),Zarankiewicz无符号拉普拉斯谱极值问题和Zarankiewicz问题以及Zarankiewicz邻接谱谱极值问题会有很大的差异.de Freitas等[56]提出了猜想6. 猜想6[56]令s≥t-1≥1和G是一个顶点数为n充分大的简单图.若G不含Kt,s+1作为子图,则 等号成立当且仅当G=Kt-1∨H, 其中H是一个顶点数为n-t+1的简单s正则图. 对于特殊的s=1,t=2, 这个猜想已被证明[46].对于所有的s,t, 他们并不能证明这个猜想或给出反例.但是对于s≥1,t=2,他们证明了猜想成立. 定理40[56]令s≥1和G是一个顶点数为n≥s2+6s+6的简单图.若G不含K2,s+1作为子图,则 等号成立当且仅当G=K1∨H, 其中H是一个顶点数为n-1的简单s正则图. 对于s+1≥t≥3, Kong等[57]给出了不含Kt,s+1作为子图的简单连通图的无符号拉普拉斯谱半径的上界,即定理41. 定理41[57]令s≥t≥3和G是一个顶点数为n≥s+t的简单连通图.若G不含Kt,s作为子图,则 q(G)≤n+(s-t+1)1/tn1-1/t+(t-1)(n-1)n1-3/t+t-3. 当H是一个完全图或完全二部图,简单图G不含H-子式谱极值问题得到了较多的研究[58-60]. Shi等[58]给出了不含K4-子式的简单图的最大谱半径,并刻画了极图. 定理42[58]令G是一个顶点数为n的简单图.若G不含K4-子式,则 Hong[59]给出了不含K5-子式的简单图的谱半径上界,并刻画了极图. 定理43[59]令G是一个顶点数为n的简单图.若G不含K5-子式,则 Tait[60]把定理42、43拓展到不含Kr-子式的图上,其中r≥3. 定理44[60]令r≥3和G是一个顶点数为n充分大的简单图.若G不含Kr-子式,则 下面考虑不含Ks,t-子式问题: 若s=t=2, 则简单图G不含K2,2-子式,且G不含K2,2作为子图,定理26意味着ρ(G)≤ρ(F2,2(n)).由于F2,2(n)不含K2,2-子式,则等号成立当且仅当G=F2,2(n). 对于s=2,t=3, Yu等[61]给出了不含K2,3-子式的简单图的谱半径上界. 定理45[61]令G是一个顶点数为n≥2的简单图.若G不含K2,3-子式,则 定理45的界不是紧的.类似地,Benediktovich[62]研究不含K2,4-子式的简单2-连通图的谱半径上界,并给出了类似定理45的结果. 注意到Fs,t(n)=Ks-1∨(pKt∪Kl), 其中n-s+1=pt+l, 0≤l 等号成立当且仅当n≡s-1 (modt)且G=Fs,t(n). Nikiforov[63]给出了不含K2,3-子式的简单图的谱半径的紧的上界,并刻画了极图. 定理46[63]令G是一个顶点数为n>40 000的简单图.若G不含K2,3-子式,则 ρ(G)≤ρ(F2,3(n)), 等号成立当且仅当G=F2,3(n). 另外,对于t≥4, Nikiforov[63]还给出了不含K2,t-子式的简单图的谱半径的紧的上界,并刻画了极图. 定理47[63]令t≥4和G是一个顶点数为n≥400t6的简单图.若G不含K2,t-子式,则 等号成立当且仅当n≡1 (modt)且G=F2,t(n). 最近,Tait[60]把定理47拓展到更一般的结果,即定理48. 定理48[60]令t≥s≥2和G是一个顶点数为n充分大的简单图.若G不含Ks,t-子式,则 等号成当且仅当n≡s-1 (modt)且G=Fs,t(n). 注意到如果t不能整除n-s+1, 定理48的界不是紧的.Tait[60]给出了对所有充分大的n都紧的猜想,即猜想7. 猜想7 令t≥s≥2和G是一个顶点数为n充分大的简单图.若G不含Ks,t-子式,则 ρ(G)≤ρ(Fs,t(n)), 等号成立当且仅当G=Fs,t(n). 如果一个图能同构于一个平面图,那么称这个图为可平面图.如果一个可平面图的所有顶点都落在外面的边界上,则这个可平面图被称为外可平面图. Wagner[64]用禁用子式给出了可平面图的充要条件:一个图是可平面图当且仅当它不包含K5-子式也不包含K3,3-子式.类似地,一个图是外可平面图当且仅当它不包含K4-子式也不包含K2,3-子式. 可平面图谱半径的研究已经有很长的历史,至少可以追溯到Schwenk等[65]的工作.Boots等[66]、Cao等[67]分别独立提出了关于可平面图得到最大谱半径的极图只有K2∨Pn-2的猜想.20多年后,这个猜想被Tait等[68]用特征向量的方法证明. 定理49[68]令G是一个顶点数为n充分大的可平面图,则 ρ(G)≤ρ(K2∨Pn-2), 等号成立当且仅当G=K2∨Pn-2. 除此之外,Tait等[68]还用特征向量的方法证明了Cvetkovic等[69]提出的外可平面图得到最大谱半径的极图的猜想,即定理50. 定理50[68]令G是一个顶点数为n充分大的外可平面图,则 ρ(G)≤ρ(K1∨Pn-1), 等号成立当且仅当G=K1∨Pn-1. Yu等[70]以及Yu等[71]分别用不同的方法证明了定理49、50对无符号拉普拉斯谱半径也成立. 定理51[70]令G是一个顶点数为n≥456的可平面图,则 q(G)≤q(K2∨Pn-2), 等号成立当且仅当G=K2∨Pn-2. 定理52[71]令G是一个顶点数为n的外可平面图,则 q(G)≤q(K1∨Pn-1), 等号成立当且仅当G=K1∨Pn-1. [1] BONDY J A, MURTY U S R. Graph theory[M]. New York: Springer, 2007. [2] MANTEL W. Problem 28[J]. Wiskundige Opgaven, 1907, 10: 60-61. [4] STANLEY R P. A bound on the spectral radius of graphs witheedges[J]. Linear Algebra Appl, 1987, 87: 267-269. [5] WILF H S. Spectral bounds for the clique and independence numbers of graphs[J]. J Combin Theory, 1986, 40 (1): 113-117. [6] NIKIFOROV V. The spectral radius of graphs without paths and cycles of specified length[J]. Linear Algebra Appl, 2010, 432 (9): 2243-2256. [7] NIKIFOROV V. Bounds on graph eigenvalues II[J]. Linear Algebra Appl, 2007, 427 (2/3): 183-189. [8] GUIDULI B. Spectral extrema for graphs[D]. Chicago: Department of Mathematics of University of Chicago, 1998. [9] NOSAL E. Eigenvalues of graphs[D]. Calgary: Department of Mathematics of University of Calgary, 1970. [10] NIKIFOROV V. Some inequalities for the largest eigenvalue of a graph[J]. Combin Probab Comput, 2002, 11 (2): 179-189. [11] NIKIFOROV V. Walks and the spectral radius of graphs[J]. Linear Algebra Appl, 2006, 418 (1): 257-268. [12] MOTZKIN T, STRAUS E. Maxima for graphs and a new proof of a theorem of Turán[J]. Canad J Math, 1965, 17: 533-540. [13] EDWARDS C S, ELPHICK C H. Lower bounds for the clique and the chromatic number of a graph[J]. Discrete Appl Math, 1983, 5 (1): 51-64. [14] NIKIFOROV V. Surveys in combinatorics[M]. London: Cambridge Univ Press, 2011: 141-181. [15] XU M M, HONG Y,SHU J L, et al. The minimum spectral radius of graphs with a given independence number[J]. Linear Algebra Appl, 2009, 431 (5): 937-945. [16] DU X, SHI L S. Graphs with small independence number minimizing the spectral radius[J]. Discrete Math Algorithm and Appl, 2013, 5 (3): 1350017. [17] JIN Y L, ZHANG X D. The sharp lower bound for the spectral radins of connected graphs with the indep endence number[J]. Taiwanse Math, 2015, 19: 419-431. [18] DE ABREU N M M, NIKIFOROV V. Maxima of theQ-index: graphs with bounded clique number[J]. Electron J Linear Algebra, 2013, 26: 121-130. [19] HANSEN P, LUCAS C. An inequality for the signless Laplacian index of a graph using the chromatic number[J]. Graph Theory Notes N Y, 2009, 57: 39-42. [20] HE B, JIN Y L, ZHANG X D. Sharp bounds for the signless Laplacian spectral radius in terms of clique number[J]. Linear Algebra Appl, 2013, 438 (10): 3851-3861. [21] ERDÖS P, GALLAI T. On maximal paths and circuits of graph[J]. Acta Math Acad Sci Hungar, 1959, 10 (3/4): 337-356. [22] BALISTER P N, GYÖRI E, LEHEL J, et al. Connected graphs without long paths[J]. Discrete Math, 2008, 308 (19): 4487-4494. [23] ERDÖS P. Hypergraph Seminar[M]. Berlin: Springer, 1974: 187-190. [24] MCLENNAN A. The Erdös-Sós conjecture for trees of diameter four[J]. J Graph Theory, 2005, 49 (4): 291-301. [25] FAN G H,SUN L L. The Erdös-Sós conjecture for spiders[J]. Discrete Math, 2007, 307 (23): 3055-3062. [26] YUAN L T, ZHANG X D. On the Erdös-Sós conjecture for graphs onn=k+4 vertices[J]. Ars Math Contemp, 2017, 13 (1): 49-61. [27] BUSHAW N, KETTLE N. Turán numbers of multiple paths and equibipartite forests[J]. Combin Probab Comput, 2011, 20 (6): 837-853. [29] YUAN L T, ZHANG X D. The Turán number of disjoint copies of paths[J]. Discrete Math, 2017, 340 (2): 132-139. [30] ZHAI M Q, LIN H Q, GONG S C. Spectral conditions for the existence of specified paths and cycles in graphs[J]. Linear Algebra Appl, 2015, 471: 21-27. [31] NIKIFOROV V, YUAN X Y. Maxima of theQ-index: graphs without long paths[J]. Electron J Linear Algebra, 2014, 27: 504-514. [32] YU G H. On the maximal signless Laplacian spectral radius of graphs with given matching number[J]. Proc Japan Acad, 2008, 84 (8): 163-166. [33] NIKIFOROV V. A spectral condition for odd cycles in graphs[J]. Linear Algebra Appl, 2008, 428 (7):1492-1498. [35] KÖVARI T, SS V, TURN P. On a problem of K. Zarankiewicz[J]. Colloq Math, 1954, 3: 50-57. [36] Reiman I. Über ein problem von K. Zarankiewicz[J]. Acta Math Hungar,1958, 9 (3/4): 269-273. [37] ERDÖS P, RÉNYI A, SS V T. On a problem of graph theory[J]. Stud Sci Math Hungar, 1966, 1 (4): 215-235. [38] FÜREDI Z. Graphs without quadrilaterals[J]. J Combin Theory, 1983, 34 (2): 187-190. [39] ZHAI M Q, WANG B. Proof of a conjecture on the spectral radius ofC4-free graphs[J]. Linear Algebra Appl, 2012, 437 (7): 1641-1647. [40] FÜREDI Z. Quadrilateral-free graphs with maximum number of edges [DB/OL]. [2017-10-07]. http: //www. math. uiuc. edu/-z-furedi/PUBS/furediC4 from 1988. [41] ERDÖS P, RÉNYI A. On a problem in the theory of graphs[J]. Magy Tud Akad Mat Kut Intéz Közl, 1962, 7: 623-641. [42] NIKIFOROV V. The maximum spectral radius ofC4-free graphs of given order and size[J]. Linear Algebra Appl, 2009, 430 (11): 2898-2905. [43] GAO J, HOU X M. The spectral radius of graphs without long cycles[DB/OL]. [2017-11-01]. https://arxiv. org/abs/1707. 04810. [44] FAVARON O, MAHÉO M, SACLÉ J F. Some eigenvalue properties in graphs (conjectures of Graffiti. II)[J]. Discrete Math, 1993, 111 (1/2/3): 197-220. [45] YUAN W L, WANG B, ZHAI M Q. On the spectral radii of graphs without given cycles[J]. Electron J Linear Algebra, 2012, 23: 599-606. [46] DE FREITAS M A A, NIKIFOROV V, PATUZZI L. Maxima of theQ-index: forbidden 4-cycle and 5-cycle[J]. Electron J Linear Algebra, 2013 (26): 905-916. [47] NIKIFOROV V, YUAN X Y. Maxima of theQ-index: Forbidden even cycles[J]. Linear Algebra Appl, 2015, 471 (10): 636-653. [48] NIKIFOROV V. An asymptotically tight bound on theQ-index of graphs with forbidden cycles[J]. Publ Inst Math (Beograd) (N S), 2014, 95 (109): 189-199. [49] YUAN X Y. Maxima of theQ-index: forbidden odd cycles[J]. Linear Algebra Appl, 2014, 458 (10): 207-216. [50] ZARANKIEWICZ K. Problem 101[J]. Colloq Math, 1951, 2: 301. [51] BABAI L, GUIDULI B. Spectral extrema for graphs: the Zarankiewicz problem[J]. Electron J Combin, 2009, 16 (1): R123. [52] NIKIFOROV V. A contribution to the Zarankiewicz problem[J]. Linear Algebra Appl, 2010, 432 (6): 1405-1411. [53] FÜREDI Z. An upper bound on Zarankiewicz’s problem[J]. Comb Probab Comput, 1996, 5 (1): 29-33. [55] SHI L S, SONG Z P. Upper bounds on the spectral radius of book-free and/orK2,l-free graphs[J]. Linear Algebra Appl, 2007, 420 (2/3): 526-529. [56] DE FREITAS M A A, NIKIFOROV V, PATUZZI L. Maxima of theQ-index: graphs with noKs,t[J]. Linear Algebra Appl, 2016, 496: 381-391. [57] KONG Q, WANG L. Upper bounds on theQ-spectral radius of book-free and/orKs, t-free graphs[DB/OL]. [2017-04-03]. https://arxiv. org/abs/1612. 03514. [58] SHI J S, HONG Y. The spectral radius ofK4-minor free graph[J]. Acta Math Appl Sinica, 2001, 5: 167-175. [59] HONG Y. Tree-width, clique-minors, andeigenvalues[J]. Discrete Math, 2004, 274 (1/2/3): 281-287. [60] TAIT M. The Colin de Verdière parameter, excluded minors, and the spectral radius[DB/OL]. [2017-05-04]. https://arxiv. org/abs/1703. 09732. [61] YU G L, SHU J L, HONG Y. Bounds of spectral radii ofK2,3-minor free graphs[J]. Electron J Linear Algebra, 2012, 23: 171-179. [62] BENEDIKTOVICH V I. Spectral radius ofK2,4-minor free graph[J]. Dokl Nats Akad Nauk Belarusi, 2015, 59: 5-12 (in Russian). [63] NIKIFOROV V. The spectral radius of graphs with noK2,t-minor[J]. Linear Algebra Appl, 2017, 531: 510-515. [64] WAGNER K. Über eine Eigenschaft der ebenen Komplexe[J]. Math Ann, 1937, 114 (1): 570-590. [65] SCHWENK A J, WILSON R J. On the eigenvalues of a graph[J]. Selected Topics in Graph Theory, 1978, 11: 307-336. [66] BOOTS B N, ROYLE G F. A conjecture on the maximum value of the principal eigenvalue of a planar graph[J]. Geogr Anal, 1991, 23 (3): 276-282. [67] CAO D S, VINCE A. The spectral radius of a planar graph[J]. Linear Algebra Appl, 1993, 187 (93): 251-257. [68] TAIT M, TOBIN J. Three conjectures in extremal spectral graph theory[J]. J Combin Theory Ser B, 2017, 126: 137-161. [69] CVETKOVIC D, ROWLINSON P. The largest eigenvalue of a graph: a survey[J]. Linear and Multilinear Algebra, 1990, 28 (1/2): 3-33. [70] YU G L, WANG J Y, GUO S G. Maxima of the signless Laplacian spectral radius for planar graphs[J]. Electron J Linear Algebra, 2015, 30: 795-811. [71] YU G L, GUO S G, WU Y R. Maxima of theQ-index for outer-planar graphs[J]. Linear and Multilinear Algebra, 2015, 63 (9): 1837-1848.3 禁用线性森林的谱Turán类型极值问题
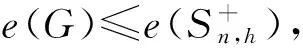
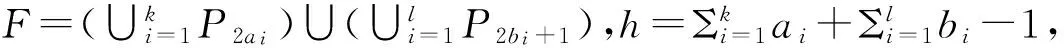
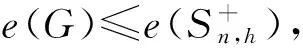


3.1 禁用线性森林的邻接谱Turán类型极值问题
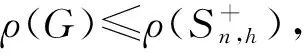
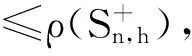
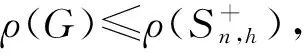
3.2 禁用线性森林的无符号拉普拉斯谱Turán类型极值问题
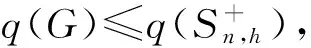
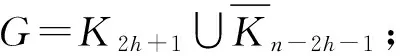
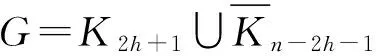
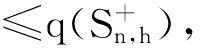
4 禁用圈的谱Turán类型极值问题
4.1 禁用圈的邻接谱Turán类型极值问题
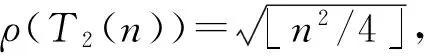
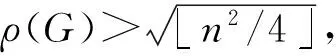

4.2 禁用圈的无符号拉普拉斯谱Turán类型极值问题
5 Zarankiewicz谱极值问题
5.1 邻接谱的Zarankiewicz谱极值问题
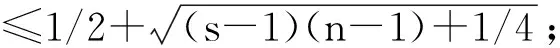
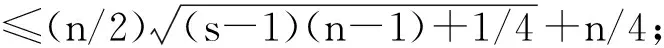
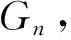
5.2 无符号拉普拉斯谱的Zarankiewicz谱极值问题
6 禁用H-子式的谱Turán类型极值问题
6.1 禁用Kr-子式或者Ks,t-子式
6.2 可平面图和外可平面图
