固体颗粒对油气井管柱的冲蚀损伤研究

刘寒月，魏 宁

(1.辽宁工程技术大学安全科学与工程学院，辽宁 葫芦岛 125105；2.矿山热动力灾害与防治教育部重点实验室，辽宁 葫芦岛 125105)

在石油、天然气以及煤层气开采过程中，钻井液中夹杂的岩屑和支撑剂等固体颗粒在流体的携带作用下以一定速度和角度冲击管柱，对管材进行冲蚀，导致管柱壁面材料损耗、壁厚变薄，降低了管材的抗挤强度和抗内压强度，极易发生管柱变形和损毁，给安全生产造成极大的隐患。为了保证石油天然气及煤层气开采过程中的管柱安全，需要对生产过程中固体颗粒对管柱的冲蚀速度和冲蚀程度进行分析，以制定相应的缓解措施。国内很多学者对固体颗粒的冲蚀理论进行了分析，并进行了冲蚀物理实验，研究油气井管柱受冲蚀的磨损机理[1-6]，但较少考虑流体中固体颗粒之间的相互碰撞等影响因素。本文对两相流中的单个固体颗粒的受力状态进行了分析，并应用湍流模型和DPM离散相模型，对90°弯管的颗粒冲蚀磨损进行了数值模拟，在分析其冲蚀磨损特性后得到了不同因素对冲蚀部位、冲蚀速率以及冲蚀量的影响规律。

1 固体颗粒对管柱冲蚀的影响因素

影响固体颗粒对油气井管柱的冲蚀程度的因素众多[3，4，6-8]，有管材的力学性能、管柱内壁的粗糙程度，以及各种外部因素，包括入射颗粒的速度、粒度、密度和体积分数、质量流率等，固体颗粒对管材的冲蚀角度、冲蚀速度、冲蚀时间，还有流体的黏度、密度、流速等性质。本文主要研究的是对同一种材料性能的90°弯曲管柱，外部环境因素的改变对管柱造成的冲蚀影响。

2 数学模型的建立

Fluent中的DPM模型把流体视为连续相，流体相为牛顿流体，把固体颗粒视为离散相，各相的物理性质不变。

2.1 湍流模型控制方程

2.1.1 连续性方程

连续性方程即质量守恒方程，对于空间固定的封闭曲面，不稳定流动时单位时间内流入控制体的总质量与流出控制体的质量之差，其表达式见式(1)[9]。

(1)

式中：ux、uy、uz分别表示x、y、z方向的速度分量，m/s；t表示时间，s；ρ表示流体密度，kg/m3。

2.1.2 动量方程

动量方程可以表达为流体微元服从牛顿第二定律，其表达式见式(2)～(4)[9]。

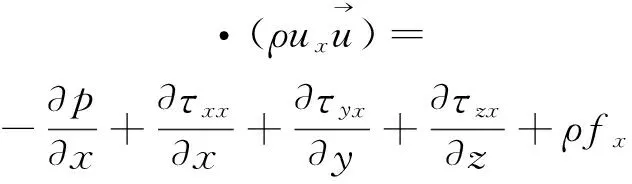
(2)

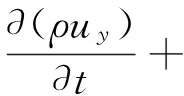
(3)

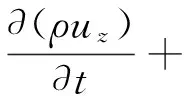
(4)

式中：ρ表示流体微元体上的压强，Pa；τxx、τxy、τxz表示由分子粘性作用产生的作用在微元体表上面的粘性应力，Pa；fx、fy、fz分别表示x、y、z方向的单位质量力，m/s2。

2.1.3 能量方程

能量方程是指包含有热交换的流动系统必须满足热力学第一定律，其表达式见式(5)[9]。

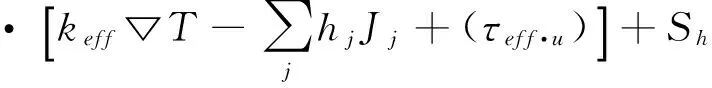
(5)

式中：E表示流体微团的总能，J/kg，包含内能、等能和势能之和，其中E=h-p/ρ+u2/2；h表示焓，J/kg，hj为组分j的焓，J/kg；keff表示有效热传导系数，W/(m·k)，keff=k+kt，kt为湍流热传导系数；Jj为组分j的扩散通量；Sh表示化学反应热及其他用户定义的体积热源项。

2.1.4k-ε湍流模型

标准的k-ε模型是基于传输方程—湍流动能k方程和耗散率ε方程建立的。在k-ε模型传输方程中，假设流体是完全湍流状态，忽略了分子粘性的影响。标准k-ε模型的运输方程见式(6)和式(7)[9]。湍流动能k方程见式(6)。耗散率ε方程见式(7)。湍流黏度μt可由湍流动能k和耗散率ε计算得到,见式(8)[9]。

Gk+Gb-ρε-YM+SK

(6)

(7)

(8)

式(6)～(8)中：Gk表示由平均速度梯度引起的湍流动能产生项；Gb表示由浮力引起的湍流动能产生项；YM表示在可压缩湍流中脉动膨胀对整体耗散率的影响值；C1ε、C2ε、C3ε为经验常数，默认C1ε=1.44，C2ε=1.92，C3ε=0.09；σk、σε表示湍流动能和湍流动能耗散率对应的普朗特数，σk=1.0，σε=1.3，Sk、Sε为用户自定义项；Cμ为经验常数，取0.09。

标准的k-ε湍流模型不仅考虑了由平均速度梯度和浮力产生的湍流动能，同时考虑了可压缩湍流中脉动膨胀对整体耗散率的影响。因此标准的k-ε模型能够模拟复杂的内流和外流以及压力梯度下的边界层流动，也能模拟快速应变、强漩涡流等复杂三维流动。

2.2 固体颗粒冲蚀模型

美国石油协会(API)提出的弯头管柱的冲蚀磨损模型见式(9)[3]。

E=5.33MV2/D2

(9)

式中：E表示冲蚀磨损率，mg/a；M表示沙粒产出速率，g/s；V表示流体速度，m/s；D表示圆管内径，mm。

本文采用Fluent中的DPM冲蚀模型。固体颗粒对于弯管内壁面的冲蚀率Rerosion可以通过对墙体边界进行监视计算得到,见式(10)[9]。

(10)

式中：C(db)表示颗粒直径函数，C(db)=1.8×10-9；f(α)表示冲蚀角度函数，f=1；α表示颗粒轨迹与壁面的冲蚀角度；v表示固体颗粒的相对速度；b(v)为颗粒相对速度的函数，b=0；Af表示受冲蚀壁面的面积。由此计算得到的冲蚀率Rerosion的单位是冲蚀磨损量/(面积·时间)。

3 单个颗粒的受力分析

在油气井管柱中，流体的作用导致固体颗粒的运动状态发生改变。因此要研究固体颗粒对管柱的冲蚀机理，就必须要研究固体颗粒的运动特性，对其进行受力分析。固体颗粒组成的离散相的体积分数小于10%，属于稀疏两相流，因此忽略颗粒间的相互作用力。假设固体颗粒为球形刚体，不考虑颗粒的变形作用[1，8，10-15]。

1) 重力表达式见式(11)。

(11)

式中:G表示颗粒的重力；db表示颗粒的直径；ρb表示颗粒的密度。

2) 流体黏性阻力重力见式(12)。

(12)

式中：x=3.7-0.65exp[-(1.5-lgReb)2/2]；vf、vb分别表示流体速度和颗粒速度，m/s；ρf表示流体密度，kg/m3；φf表示流体的体积分数；kD表示流体的阻力系数，kD=(0.63+4.8/Reb)2；Reb为颗粒雷诺数。

3) 压力梯度力。在有压强梯度的流体中，总有压强的合力作用在颗粒上。假定颗粒所处的流场范围内压强梯度∂p/∂y为常数，则球形颗粒所受到的压力梯度力见式(13)。

(13)

4) 附加质量力。颗粒的附加质量力是颗粒加速运动时流体质量作用于颗粒上的附加力，与颗粒的加速度方向相反，表达式见式(14)。

(14)

4 数值模拟

4.1 几何模型

模型采用的管柱材料为N80钢，密度为7 850 kg/m3，弹性模量为2.06×105MPa，泊松比为0.3，屈服强度551.6 MPa；弯管外径88.9 mm，内径75.9 mm，弯头两端各伸出500 mm，弯曲半径152 mm[8]。喷射的固体颗粒直径0.45 mm，密度为2 600 kg/m3，颗粒体积含量为5%；流体黏度为0.02 Pa·s，密度为1.0×103kg/m3。

4.2 网格划分和边界条件

油气井管柱的弯管模型共划分为648 372个网格。由于弯曲壁面受到的颗粒冲蚀最严重，因此弯曲面对网格要求的精度更高，对其进行特殊处理，网格比例因子为1.3，划分为5层。网格的最小尺寸为3 mm，数值模型的时间步长设置为0.000 5 s。

入口设置为速度入口，流体的速度设置为22 m/s，湍流强度为0.16Re-1/8，其中流体雷诺数Re=ρfvfdg/μt，dg为圆形管道的横截面当量直径。水力直径设置为圆形截面管道的内径，出口为自由出口；壁面属性选择stationary wall，满足无滑移条件，边界类型设置为reflect，反弹系数由壁面碰撞恢复系数决定。

4.3 计算结果分析

在两相流的耦合计算中，先计算得到收敛或部分收敛的连续相流场，然后创建喷射源，在计算域中引入离散相进行耦合计算。固体颗粒喷射速度与入口流体速度一致。共迭代4 000步，期间共喷射固体颗粒1 608 000个。

固体颗粒对管柱壁面的冲蚀磨损是大量粒子长期作用的结果，而且管壁的大部分区域无明显磨蚀损伤，只会在局域区域产生明显磨损，造成管柱系统失效。因此本文研究颗粒对管柱内壁造成的平均冲蚀率而不是壁面平均冲蚀量。对弯曲管道来说，固体颗粒对管壁造成的冲蚀磨损最严重的区域发生在弯曲处，随着弯曲角度的增加磨蚀加重，在60～90°间的磨蚀最严重。如图1(a)所示，固体颗粒对弯管的冲蚀磨损主要发生在弯头的外弧内壁，平均冲蚀率达到了1.67×10-7kg·m-2·s-1。上弯头和下弯头处的冲蚀磨损程度和冲蚀面积都不相同，其中下弯头受冲蚀磨损的程度更加严重，冲蚀面积更大。对于弯管的入口来说，几乎不受固体颗粒的冲蚀影响，但在弯管的出口水平直管部分发生了明显的冲蚀磨损。

图1(b)为流体对壁面造成的冲蚀压力分布图。可以看出，弯管内壁面的最大冲蚀压力位于弯曲段，其中弯曲段外弧内壁压力明显大于内弧内壁所受到的流体压力，流体中的固体颗粒在弯管外弧段密集度增大，而内弧部分固体颗粒分布稀少。

采用颗粒随机跟踪模型对固体颗粒的运动轨迹进行跟踪，如图1(c)所示。颗粒由直管段进入弯曲段时运动轨迹发生了变化，这是由于在弯曲段外弧部分流体速度减慢，内弧部分流速加快，颗粒分布稀疏，如图1(d)所示。图1(a)～(d)从流体压力、流体速度以及颗粒轨迹跟踪等方面验证了图1(a)的结果，弯管内壁冲蚀最严重的部位集中在弯管的下弯头部分。

分别对不同工况下流体黏度、流体速度、固体颗粒直径、冲蚀时间影响下的固体颗粒冲蚀进行数值模拟，工况参数如表1所示。图2～7为不同因素影响下弯管受固体颗粒冲蚀结果。

从图2～7可以看出，固体颗粒对油气井管柱弯管的冲蚀磨损受流体黏度、流体速度、固体颗粒直径、冲蚀时间等因素的影响很大。由图2～4可知，在流体速度一定的情况下，固体颗粒对弯曲内壁的冲蚀量随着流体黏度的增大而减小，随着固体颗粒直径的增大而增大，随着冲蚀时间的增加而呈线性增加。而由图5～7可以看出，在流体黏度、固体颗粒直径以及冲蚀时间一定的情况下，固体颗粒对弯曲内壁的冲蚀量随着流体速度的增大而增大，但是增加趋势较为缓慢，增量逐渐减小。

图1 固体颗粒对管柱壁面的冲蚀结果

影响因素流体黏度/(Pa·s)流体速度/(m·s-1)固体颗粒直径/mm冲蚀时间/s固体颗粒质量流率/(kg·s-1)参数值0.002130.2510.10.011220.3520.50.020310.4531.00.029400.5541.5

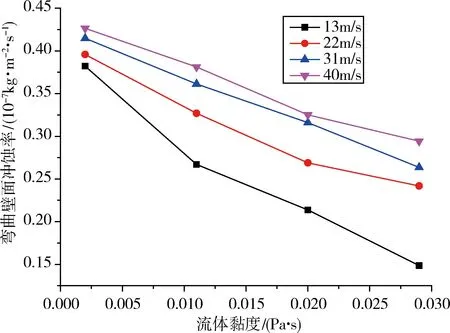
图2 不同流体速度下平均冲蚀率与流体黏度的关系

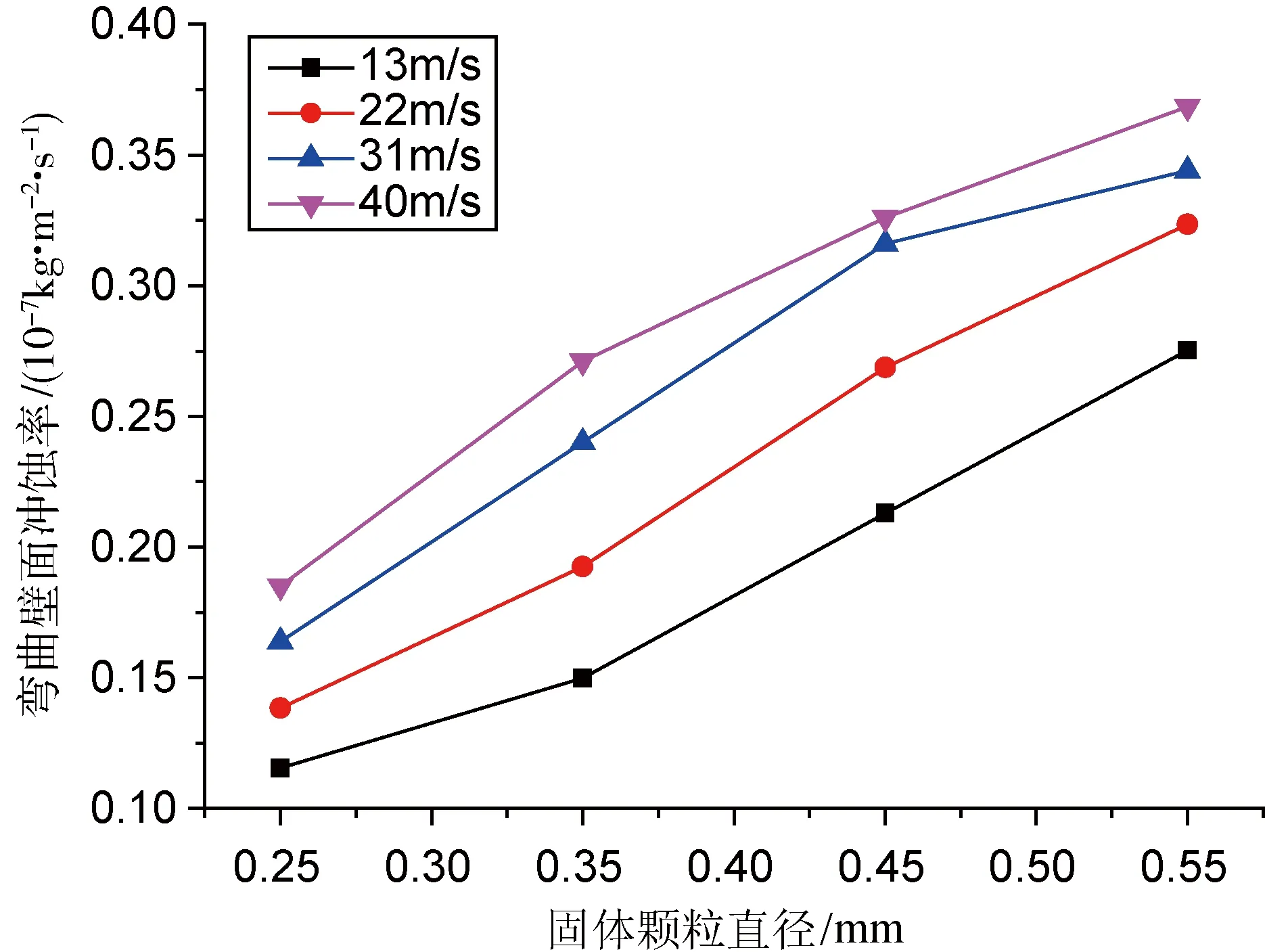
图3 不同流体速度下平均冲蚀率与固体颗粒直径的关系

图4 不同流体速度下平均冲蚀率与冲蚀时间的关系

图5 不同流体黏度下平均冲蚀率与流体速度的关系

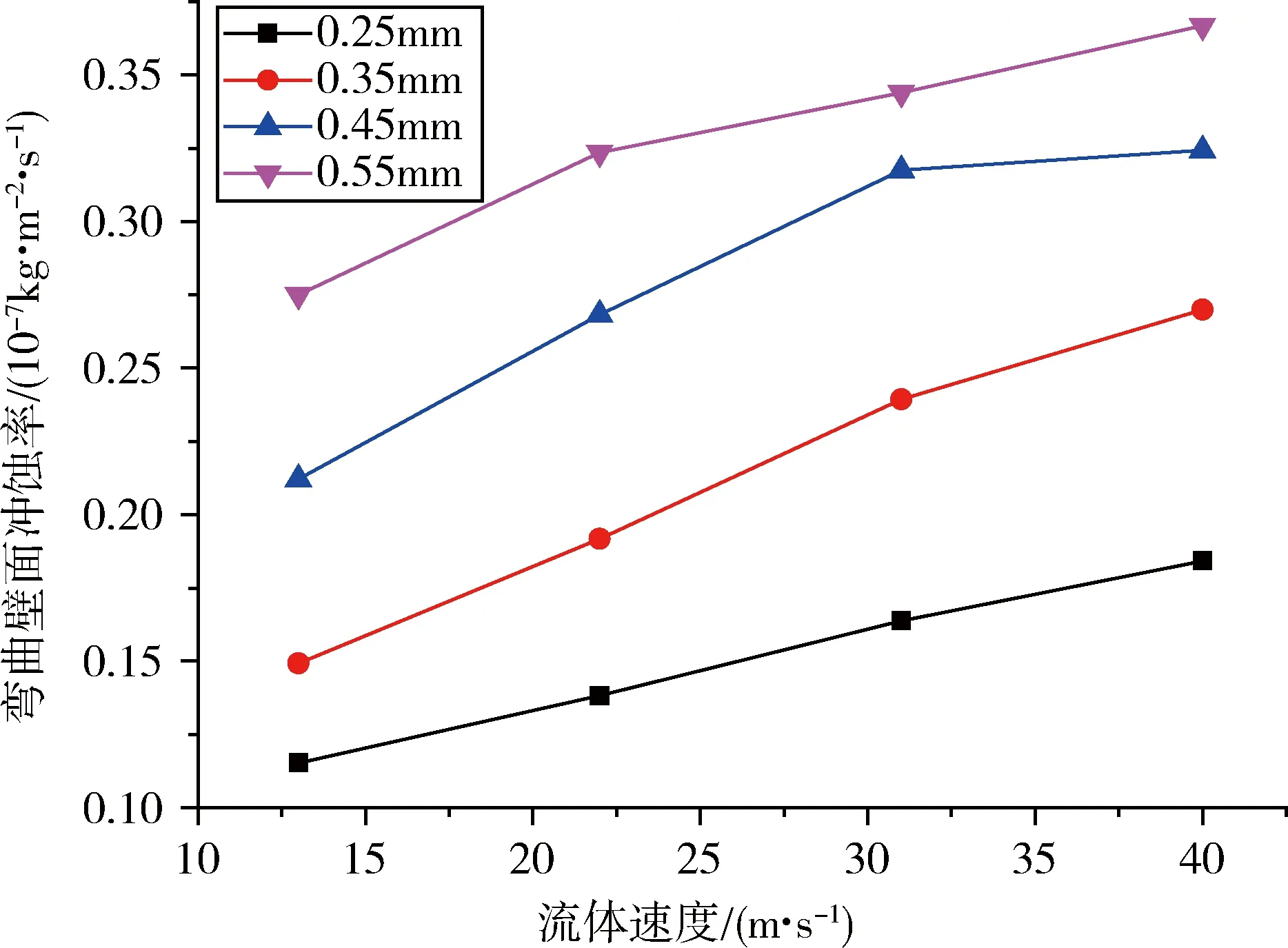
图6 不同固体颗粒直径下平均冲蚀率与流体速度的关系

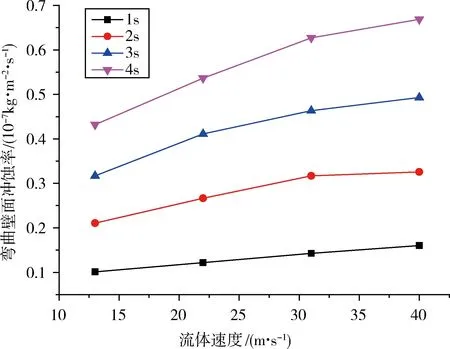
图7 不同冲蚀时间下冲蚀量与流体速度的关系

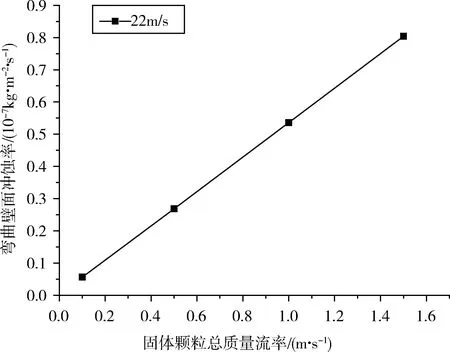
图8 冲蚀量与颗粒质量流率的关系

颗粒的总质量流率也是个非常重要的影响参数，在流体入口速度22 m/s，流体黏度0.02 Pa·s，固体颗粒直径0.45 mm，冲蚀时间为1 s的情况下，分别对质量流率为0.1 kg/s、0.5 kg/s、1.0 kg/s和1.5 kg/s时的固体颗粒冲蚀进行数值模拟，得到的固体颗粒质量流率-冲蚀量曲线如图8所示。

从图8可以看出，在其他环境因素一定的情况下，随着固体颗粒质量流率的增加，冲蚀量线性增大。对其进行拟合，得到弯曲壁面的冲蚀磨损量与固体颗粒的质量流率之间的关系拟合式为式(13)。

y=a+bx

(13)

式中：a=0.02，b=0.534 41，相关系数为0.99。

由此可知，弯曲管道受固体颗粒冲蚀磨损影响较大的外部环境因素为流体黏度、颗粒直径、冲蚀时间和颗粒质量流率，受流体速度影响相对较小，但不可忽视。

5 结 论

对不同流体黏度、流体速度、颗粒直径和冲蚀时间等多种工况下油气井管柱弯管受固体颗粒的冲蚀磨损进行了数值模拟，得出如下结论。

1) 固体颗粒对弯管的冲蚀磨损主要发生在弯曲段的外弧内壁，其中下弯头受冲蚀磨损的程度更加严重，冲蚀面积更大，在弯管的出口水平直管部分发生了明显的冲蚀磨损。

2) 在流体速度一定的情况下， 固体颗粒对弯曲

内壁的冲蚀率随着流体黏度的增大而减小，随着固体颗粒直径的增大而增大，随着冲蚀时间的增加而呈线性增加；在流体黏度、固体颗粒直径以及冲蚀时间一定的情况下，固体颗粒对弯曲内壁的冲蚀率随着流体速度的增大而缓慢增大，增量逐渐减小；在其他环境因素一定的情况下，随着固体颗粒质量流率的增加，冲蚀量呈线性增加。

3) 可通过适当减小流体速度、采取分离措施尽可能减小固体颗粒粒径、以及适当增加管材厚度来降低固体颗粒对油气井管柱的冲蚀磨损影响。

[1] 安杰.油气井管柱受颗粒冲蚀的数值模拟[D].荆州：长江大学，2014.

[2] 吕函珂.基于DEM的细长型金属管粉体颗粒夯实的模拟研究[D].重庆：重庆大学，2013.

[3] 黄勇，蒋晓东，施哲雄.弯头的冲蚀问题及其预测和预防[J].炼油技术与工程，2005，35(2)：33-36.

[4] 冯进，张慢来，冯仲.带粒液流中圆形弯管的冲蚀模型研究[J].长江大学学报：自然科学版，2008，5(3)：74-76.

[5] 李国美，王跃社，黄刚，等.套管壁面颗粒冲蚀预测及减弱措施研究[J].石油机械，2010，38(1)：20-24.

[6] 郑友取，张新育.90°方形弯管内颗粒冲蚀磨损研究[J].热力发电，2007，36(4)：34-37.

[7] 李瑞霞，柳朝晖，贺铸，等.各向同性湍流内颗粒碰撞率的直接模拟研究[J].力学学报，2006，38(1)：25-32.

[8] 易卫国，杨谦，李群松.稀薄颗粒流体对弯管冲蚀的数值模拟[J].湖南师范大学自然科学学报，2012，35(5)：56-59.

[9] Fluent，A.ANSYS FLUENT 14.5 Theory Guide[R].2012.

[10] Tabakoff，W，A Hamed.Aerodynamic Effects on Erosion in Turbomachinery[C].Tokyo：TSME and ASME Paper 70 Proceedings of the 1977 Joint Gas Turbine Congress，1977.

[11] Grant，G，Tabakoff W.Erosion Prediction in Turboma-chinery Resulting from Environmental Solid Particles[J].Journal of Aircraft，2012，12(5)：471-478.

[12] 王嘉琦.固-液两相磨粒流中对于颗粒碰撞结构化表面的研究[D].杭州：浙江工业大学，2012.

[13] 张强强.基于DEM-CFD耦合的颗粒在水中沉降过程仿真分析[D].长春：吉林大学，2014.

[14] 曹立虎，张遂安，石慧宁，等.沁水盆地煤层气水平井井筒煤粉迁移及控制[J].石油钻采工艺，2012，34(4)：93-95.

[15] 綦耀光，张芬娜，刘冰，等.煤层气井产气通道内煤粉运动特征分析[J].煤炭学报，2013，38(9)：1627-1633.