考虑固体变形与表面扩散的页岩气藏数值模拟

潘荣莹，古 斌，张正才

(西南科技大学制造科学与工程学院，四川 绵阳 621010)

页岩气作为一种特殊的非常规天然气，以分布广泛、气藏资源丰富、开产周期长、开发潜能大等特点成为缓解油气资源消费与供需矛盾的重要资源之一，目前已逐渐成为学者们的研究热点问题。页岩气通常以吸附态与游离态的形式赋存于页岩颗粒和微纳米孔隙中，这使得天然气在页岩中的流动不仅仅局限于黏性流，因此只考虑黏性流动的Darcy定律不再适用于描述页岩气在储集层中的流动。为了全面描述页岩和其他致密岩气藏内的多种流动机制耦合的运移规律，研究者们提出视渗透率概念并给出了不同的视渗透率模型。Javadpour[1]结合Knudsen扩散和滑脱流动效应，推导了致密岩层纳米孔隙中气体传输的视渗透率模型。Chen等[2]利用加权平均法考虑了黏性流、Knudsen扩散和气体吸附等多重运移机制，给出了简化的视渗透率模型。利用考虑多种流动机制的视渗透率模型，樊冬艳等[3]研究了页岩气藏的水平井压裂。但在上述视渗透率模型中，均未考虑开采过程中由于储层压力变化和页岩基质收缩引起的渗透率变化。Zhang等[4]考虑有效应力和吸附应变引起的页岩基质变形，建立新的孔隙率模型，并结合粘性流的Darcy定律，对煤层气的运移进行了有限元研究。在此基础上，Cao等[5]利用考虑Knudsen扩散的视渗透率模型修正Darcy定律，讨论了固体变形和流动机制对页岩气运移的影响，发现两种因素的贡献均不可忽略。吴克柳等[6]指出由于大量页岩气以吸附态的形式存在，表面吸附扩散对页岩气的流动有着重大的影响。至今，同时考虑包含表面吸附扩散的多重流动机制以及页岩变形影响的页岩气运移研究还未见相关研究。本文利用考虑表面吸附扩散的视渗透率模型，耦合有效应力和吸附应变引起的页岩基质变形，对页岩气的运移进行数值研究。重点讨论表面吸附扩散、页岩初始孔隙率和渗透率对表征页岩运移机制的视渗透率和Knudsen数的影响。

1 基本假设和控制方程

本文的工作基于以下假设：①页岩处于等温状态；②页岩为各向同性的均匀弹性孔隙介质；③孔隙内气体为理想饱和气体，黏性系数为常值；④气体的渗透为各向同性；⑤气体吸附遵循Langmuir类型吸附规律；⑥孔隙内只有单相气体。

1.1 基质变形控制方程

对各向同性的均匀孔隙弹性介质，考虑气体吸附应变时的几何方程，本构方程和准静态平衡方程可分别表示为式(1)～(3)[4,7]。

(1)

(2)

▽·σ+f=0

(3)

式中：u、ε、σ、f分别代表位移矢量、应变张量、应力张量和体积力矢量；G、ν、K分别为页岩基质的剪切模量、泊松比和体积模量；α=1-K/Ks为Biot系数，Ks为页岩颗粒的体积模量；εv为页岩体积应变；p为页岩孔隙内的气体压力；εad表示气体解吸附所引起的应变，实验证实其变化规律符合Langmuir曲线[8]，可通过Langmuir方程式(4)计算。

(4)

式中：εL为Langmuir体积应变常数；PL为Langmuir压力常数。

综合式(1)～(4)，可得由位移分量表示的页岩基质变形控制方程，见式(5)。

(5)

1.2 气体流动控制方程

孔隙内气体质量守恒定律表达式见式(6)。

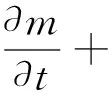
(6)

式中：m为气体质量；ρg为气体密度；v为气体流动的速度矢量；Q0为外部气体源。

气体质量m包括吸附气和自由气，可表示为式(7)。

(7)

式中：φ为页岩孔隙率；ρga为标准状态下气体的密度；ρm为页岩密度；VL为Langmuir体积常数。此外，孔隙内理想气体的状态方程式见式(8)。

(8)

式中：Mg为气体的摩尔质量；R为理想气体常数；T为温度。根据视渗透率模型假设，页岩孔隙中气体的流动速度与压力依然遵循Darcy定律的形式，只是其中的固有渗透率用视渗透率代替，见式(9)。

(9)

式中：kapp代表视渗透率；μ为气体的动力粘性系数。将式(7)～(9)代入式(6)可得式(10)。

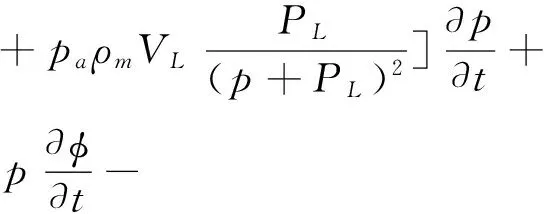
(10)

式中，pa为标准大气压。

由于页岩变形的影响，页岩的孔隙率会发生改变，变形后的孔隙率可通过不同的孔隙率模型得到。本文采用文献[4]中建立的孔隙率模型，其形式表示为式(11)。

(11)

式中：φ0为页岩初始孔隙率；S=εv+p/Ks-εad；S0=p0/Ks-εad0。

式(11)代入式(10)，可得到Darcy-storage形式的气体流动控制方程式，见式(12)。

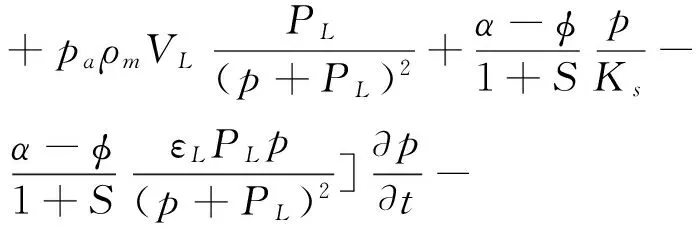
(12)

1.3 视渗透率模型

对页岩等致密岩层，其固有渗透率的改变可通过Cubic法则(式(13))计算。

(13)

式中，k∞和k∞0分别是页岩固有渗透率和初始固有渗透率。

由于气体流动的动态效应，气体在页岩基质中的流动通常包括黏性流、Knudsen扩散以及分子扩散等[3]。当考虑黏性流和Knudsen扩散时，基于Beskok-Karniadakis滑移模型的视渗透率可写为式(14)[5]。

kapp=k∞f(Kn)

(14)

式中：Kn表示Knudsen数，定义为分子平均自由程与孔隙直径的比值，见式(15)。

Kn=λ/d

(15)

(16)

若在视渗透率模型中再引入表面吸附扩散的影响，结合式(14)和式(16)，视渗透率可写为式(17)[3]。

(17)

式中：Cadmax为气体的最大吸附浓度；Dad为表面扩散系数。文献[6]的研究指出表面扩散系数不为常数，而是随着压力变化，可利用式(18)计算。

(18)

式中，Dad0为气体覆盖度为0时的表面扩散系数。

结合式(17)和式(18)，式(5)和式(12)给出了以变形位移和孔隙压力为基本未知量的页岩气运移过程流固耦合的控制方程。上述一系列方程可利用软件COMSOLMultiphysics进行数值求解。

2 数值模拟和讨论

2.1 数值模型

为阐明固体变形和不同流动机制对气体运移的影响，本文模拟了单轴应变条件下，面积为0.1 m×0.1 m的页岩中气体运移的过程，数值模型如图1所示。

图1 单轴应变条件下的页岩气运移的数值模型

其中，在软件中需要设置的固体和流体边界条件分别如下所示。

此外，流体场计算相关的初始条件为：p(0)=p0。

计算中的参数取值见表1[8]。

2.2 计算结果和讨论

一般来说，视渗透率表征页岩气在基质孔隙中的流动能力，另外，根据Knudsen数的取值，可将气体的流动分成不同的状态，见表2[5]。

因此，本工作重点关注视渗透率和Knudsen数随压力的变化规律，比较视渗透率变化与固有渗透率变化的差别，主要讨论表面扩散系数、初始孔隙率和初始渗透率的影响。

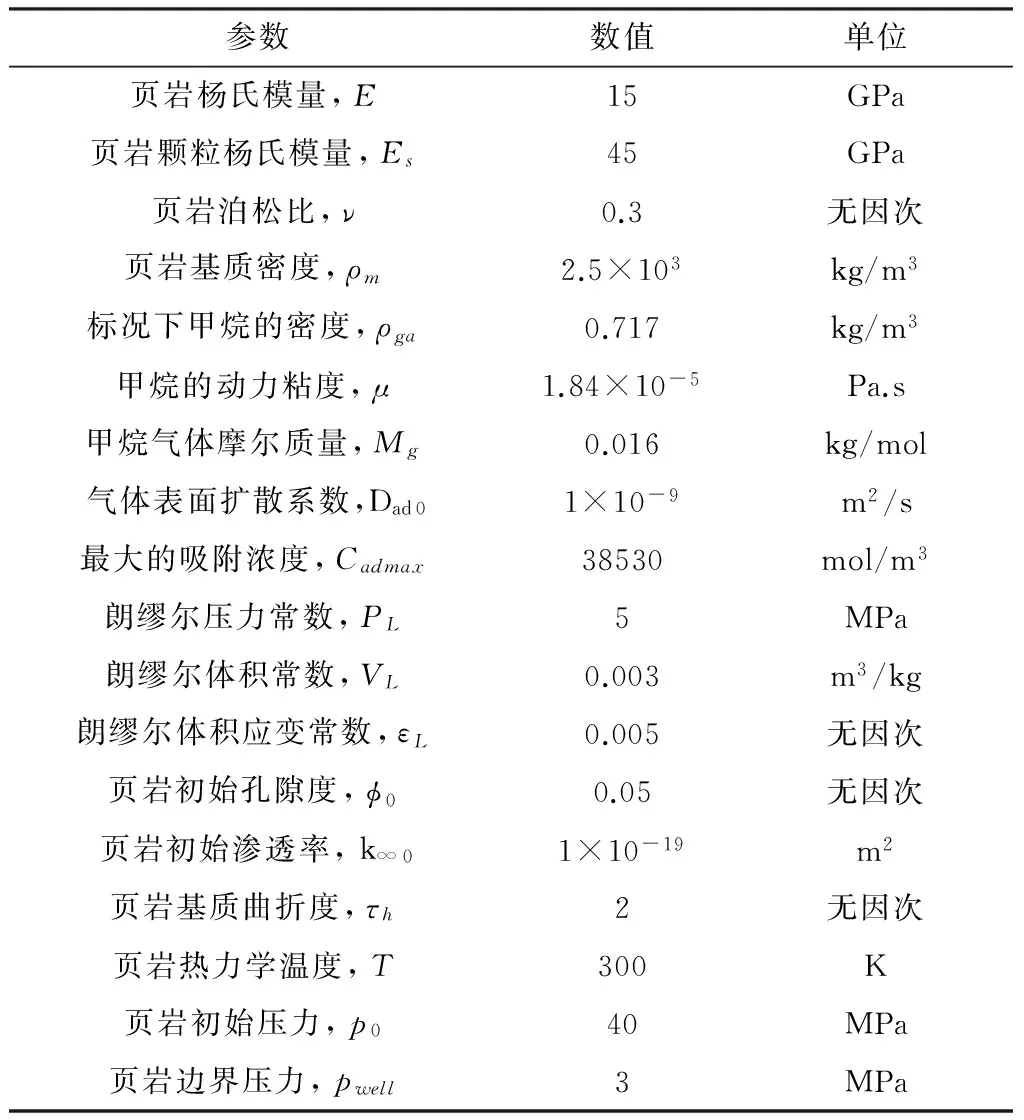
表1 数值计算中的参数取值

表2 基于Knudsen数的流动状态分类

2.2.1 表面扩散系数的影响

图2和图3给出了不同表面扩散系数时，Knudsen数以及视渗透率和固有渗透率随孔隙压力变化的曲线。其中视渗透率和固有渗透率均以页岩初始固有渗透率做无量纲化处理，同时曲线包括当表面扩散系数为常数，不随压力变化的情况。从图2可以看出，对于任意的表面扩散系数，Knudsen数随着压力的降低而逐渐升高，表明气体的流动状态已不再局限于Darcy流动。而不同的表面扩散系数对Knudsen数随压力变化的规律没有影响，则表明表面吸附扩散和微纳孔隙内气体流动的动态效应是两种相互独立的流动机制。

图3显示对于任意的表面扩散系数，视渗透率随着压力的降低而增大，而在相同压力条件下，随着表面扩散系数的增加视渗透率也逐渐增加，尤其在低压情况下视渗透率的变化达到近60%。若进一步增大表面扩散系数，其贡献将超过Knudsen扩散对视渗透率的影响。此外，相比表面扩散系数随压力变化的情况而言，表面扩散系数保持常值时的视渗透率更低。另一方面对于任意的表面扩散系数，固有渗透率随着压力的减小先降低然后升高，这是由于压力降低使得更多的吸附在页岩中开始发生气体解吸，随着气体解吸会使得页岩的渗透率增加[4]。在解吸附和压力降低两种相互竞争的机制影响下，固有渗透率表现出先降后升的变化规律。另外可以看出表面扩散系数的改变对固有渗透率与压力的关系无影响。从图3还可以看出，相对视渗透率的变化，固有渗透率的变化很小，这说明固体变形对气体流动能力的影响很小。

图2 不同表面扩散系数时Knudsen数随压力变化曲线

图3 不同表面扩散系数时渗透率比值随压力变化曲线

应当注意的是，随着页岩气运移过程的进行，会同时发生孔隙压力降低、气体解吸附加快、Knudsen数增加以及表面吸附扩散增强等现象。其中孔隙压力降低通过降低固有渗透率导致视渗透率减小，而气体解吸附加快、Knudsen数增加和表面吸附扩散增强则会提高气体流动的视渗透率。因此，当考虑固体变形和多重流动机制的耦合效应时，视渗透率将受到几种相互竞争机制的影响，其变化趋势可能因不同页岩性质和地层环境的影响而表现出与本文不同的规律。

2.2.2 初始孔隙率和固有渗透率的影响

页岩初始孔隙率和固有渗透率是表征页岩性质的两个最重要的参数，对页岩气在微纳孔隙中的流动有很大的影响。首先讨论初始孔隙率对Knudsen数和渗透率的影响(图4和图5)。由图4、图5中可以看出，随着初始孔隙率的升高，相同压力下的Knudsen数和视渗透率增加。但对固有渗透率而言，当压力较高时，更低的初始孔隙率导致更高的固有渗透率。当压力降低至某一值时，低初始孔隙率给出更小的固有渗透率。另外，当初始孔隙率很小时(φ0=0.01)，视渗透率随压力的降低表现出先轻微下降然后大幅上升的趋势，说明在低初始孔隙率时，压力降低对视渗透率的影响更加明显。但随着初始孔隙率的增加，视渗透率随着压力的降低单调升高。对于任意的初始孔隙率，固有渗透率则始终表现出先降后升的趋势。只是当初始孔隙率较小时，固有渗透率下降得更快。

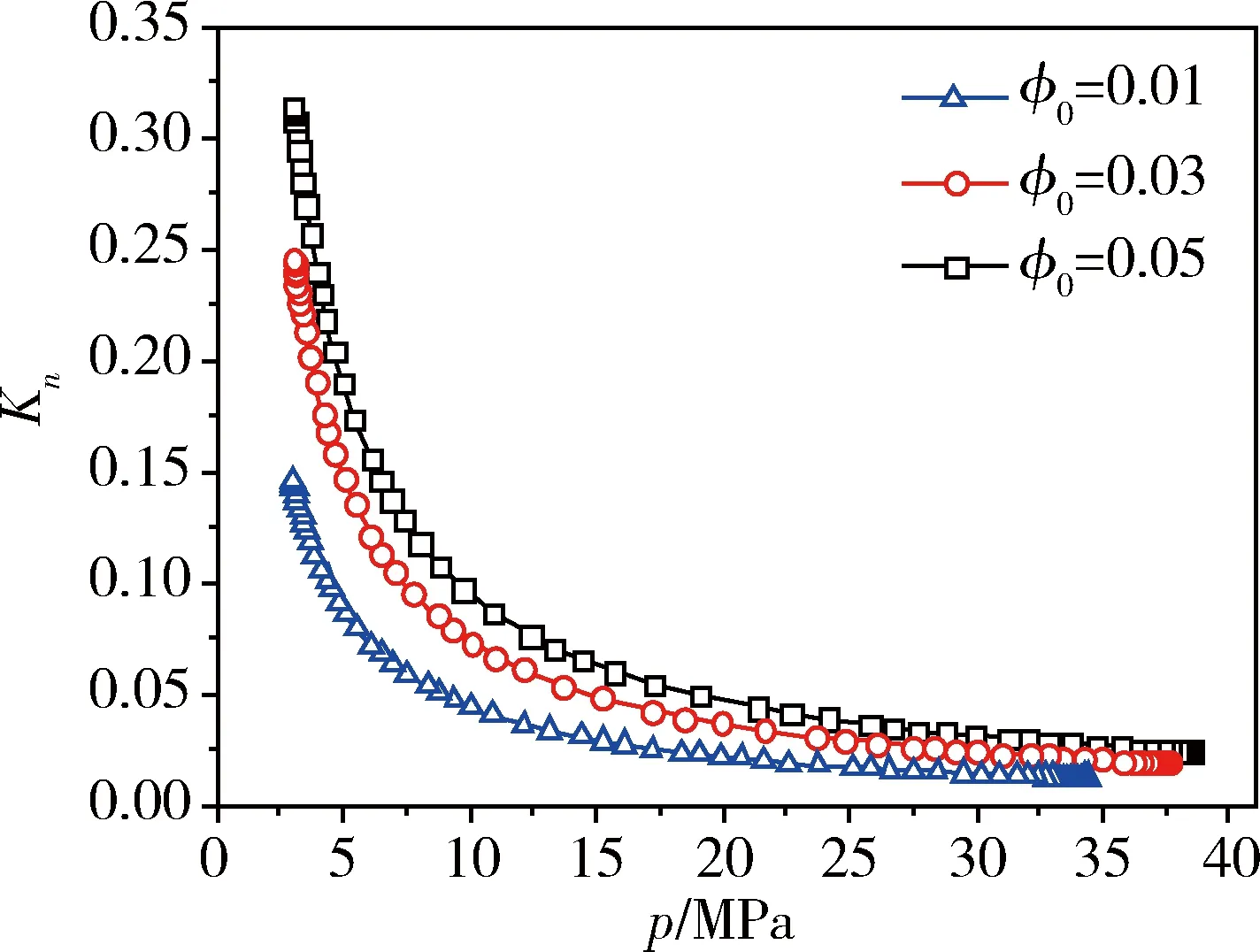
图4 不同初始孔隙率时Knudsen数随压力变化曲线

图5 不同初始孔隙率时渗透率比值随压力变化曲线

图6和图7分别给出了不同初始固有渗透率时，Knudsen数和两种渗透率随压力变化的曲线。图6、图7中结果说明，当孔隙压力一样时，更高的初始渗透率将导致更低的Knudsen数和更小的视渗透率比值，但初始渗透率的改变对固有渗透率的变化不产生影响。同时对于任意的初始渗透率，Knudsen数和视渗透率比值随着压力的降低单调增加，而固有渗透率依然呈现先降低后升高的趋势。

图6 不同初始固有渗透率时Knudsen数随压力变化曲线

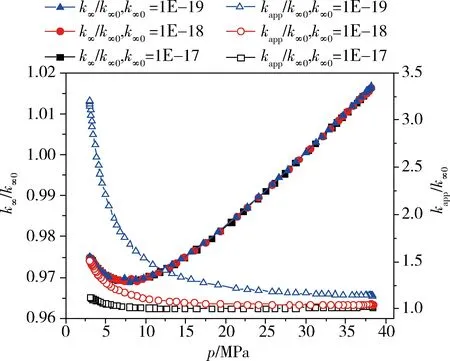
图7 不同初始固有渗透率时渗透率比值随压力变化曲线

3 结 论

考虑固体变形以及黏性流、Knudsen扩散和表面吸附扩散等多种流动机制，本文对页岩气的运移进行了数值模拟研究，得到以下结论。

1) 表面吸附扩散是与Knudsen扩散相互独立的一种流动机制，对页岩气的运移有着重要的影响，并随着扩散系数的增加表面吸附扩的影响更明显。同时当在低压阶段，表面吸附扩散对视渗透率的影响可能超过Knudsen扩散。

2) 页岩的初始孔隙率越高，页岩气运移过程中

Knudsen数和视渗透率也越高。与之相反，初始固有渗透率越高，Knudsen数和视渗透率比值越低。

3) 页岩气运移过程中，Knudsen数、视渗透率和固有渗透率的变化取决于压力、解吸附、Knudsen扩散和表面吸附扩散等多种因素相互竞争作用的结果。

[1] Javapour F. Nanopores and Apparent Permeability of Gas Flow in Mudrocks (Shale and siltstone) [J]. Journal of Canadian Petroleum Technology, 2009, 48(8): 16-21.

[2] CHEN F F , DUAN Y G, WANG K, et al. A novel pressure transient response model considering multiple migration mechanisms in shale gas reservoir[J].Journal of Natural Gas Science and Engineering, 2015, 22: 321-334.

[3] 樊冬艳, 姚军, 孙海, 等. 考虑多重运移机制耦合页岩气藏压裂水平井数值模拟[J]. 力学学报，2015, 47(6): 906-915.

[4] ZHANG H B, LIU J S, Elswortgh D. How sorption-inducedmatrix deformation affects gas flow in coal seams: A new FE model[J]. International Journal of Rock Mechanics & Mining Sciences, 2008, 45: 1226-1236.

[5] CAO P, LIU J S, LEONG Y K. Combined impact of flow regimes and effective stress on the evolution of shale apparent permeability[J]. Journal of Unconventional Oil&Gas Resources, 2016, 14: 32-43.

[6] 吴克柳, 李相方, 陈掌星. 页岩纳米孔吸附气表面扩散机理和数学模型[J]. 中国科学: 技术科学, 2015, 45(5):525-540.[7] Detournay B E,Cheng A H-D.Fundamentals of poroelasticity[C]. In: Fairhurst, 1993:113-171.

[8] YUAN W N, PAN Z J, LI X, et al. Experimental study and modelling of methane adsorption and diffusion in shale[J]. Fuel, 2014, 117: 509-519.

[9] ZHANG H X, LIU W Q, LI Z. Fracture permeability model and experiments of shale gas reservoirs[J]. Rock and Soild Mechanics, 2015, 36(3): 719-729.