基于全要素生产率视角资源型城市低碳转型效果评价模型

谭玲玲，肖 双

(1.山东工商学院工商管理学院，山东 烟台 264000；2.山东能源经济协同创新中心，山东 烟台 264000；3.山东工商学院经济学院，山东 烟台 264000)

0 引 言

随着资源型城市数十年的开采发展，大部分资源型城市已进入稳定期甚至衰退期，出现诸如经济基础薄弱、生产要素匮乏、产业结构布局不合理、社会保障能力乏力、生态衰退、环境污染等众多社会矛盾和问题，特别是在“低碳经济”成为绝大多数国家经济发展模式的趋势下，许多资源型城市纷纷提出低碳转型，构建低碳城市的目标。中央政府从2008年3月开始分三批次共界定69个资源枯竭城市，并对这些城市的转型给予扶持与特殊政策支持。各资源型城市在经过产业结构升级，培育非资源型替代产业，推广低碳技术等途径下，环境得到很大程度改善，经济的增长对资源依赖性减弱，大部分资源型城市低碳转型都取得不同程度效果。资源型城市低碳转型包括环境、经济、资源、社会等方面，因此国内学者也从不同角度建立指标体系并对其效果进行评价。有些学者对评价资源型城市转型效果指标体系的建立进行研究，如辛玲[1]在剖析低碳城市内涵的基础上，提出一个全面有效的转型评价指标体系的构建应考虑经济、基础设施、生活方式、低碳技术等六个方面；杨波[2]从经济发展系统、社会发展系统、资源禀赋系统、生态坏境系统和人力资源系统五方面构建资源型城市效果评价指标；袁晓玲等[3]从发展能力和低碳排放两方面建立指标体系，并对29个城市的低碳经济发展情况进行实证分析；李友俊[4]从低碳意识、碳源控制、低碳产业、低碳制度等八个方面构建指标体系，运用模糊层次分析法与数据包络分析法将大庆市与保定、天津的低碳发展水平进行比较。有些学者对低碳转型效果评价的方法进行研究，如赵海云等[5]、姜传军等[6]对资源型城市的经济转型效果评价采用的是层次分析法；李晓燕[7]、王小李等[8]对资源型城市低碳发展程度运用的是模糊层次分析法；安果等[9]则将熵值理论运用到评价方法中，构建熵值-灰色系统评价模型。还有些学者运用TOPSIS方法从不同角度对特定城市低碳转型效果进行评价，并提出相应对策建议，如马丽等[10]对伊春市的转型效果进行评价，从而提出设立专项基金，制定优惠政策、合理制定发展规划等有利于林业资源型城市转型的对策建议；王学军等[11]研究焦作市的转型效果，研究指出从2012年开始焦作市的低碳转型阶段从初级跃进中级，转型趋势较好；张荣光等[12]对攀枝花市的转型效果进行分析，并提出优化产业结构，加大环保力度，改善能源结构等对策建议。

目前，很多学者从不同角度构建指标体系来评价低碳转型的效果，但现有研究的评价方法和指标的选择都比较分散，有的侧重经济转型，有的侧重环境改善，还有的仅限于对指标体系构建的原则及方法进行研究，并没有结合具体的城市进行评价和研究。然而，从全要素生产率(TFP)角度来评价资源型城市低碳转型效果，不仅能考虑投入、产出指标的关系，还能避免遗漏对环境有严重影响的非期望产出。Pittman[13]指出为测算合理的TFP，必须考虑期望产出和非期望产出；Chung等[14]指出忽略污染等非期望产出将会导致测算的TFP存在偏差。过去的发展中，资源型城市在得到高速增长的国民生产总值的同时，也必然得到严重污染环境的非期望产出，比如废水、废弃、固体废弃物等。而在资源型城市转型过程中，广泛地将低碳技术和绿色能源运用到产业生产过程中，同时非常注重对环境的改善，因此在城市进行低碳转型过程中，生产过程中产生的非期望产出应该伴随着转型效果的体现而逐渐减少。因而，本文以17个资源型城市为例，采用2008～2015年的面板数据，选取基于方向性距离函数的DEA(数据包络分析)模型测算城市的全要素生产率，将对环境产生负面影响的非期望产出纳入模型中，用考虑非期望产出的全要素生产率测度模型来对资源型城市低碳转型效果进行评价。

1 包含非期望产出的TFP测度模型

1.1 数据包络分析

数据包络分析(Data Envelopment Analysis)简称DEA，从1978年由运筹学家Charnes，Cooper等人提出至今，已经发展成为运筹学、管理科学、系统科学交叉研究的一个新的领域，并在这些领域得到广泛地应用，是一种对相似决策单元(DMU)多投入多产出的相对效率评价方法。DEA是一种非参数评估方法，在评价过程中不需要投入产出间明确的函数表达式，对权重和参数也无需主观估计和假设，因此DEA本身具有减少误差，消除主观因素和简化运算的自身优势。传统DEA模型在测度DMU相对效率时，要求以最小资源投入实现最大的产出，忽略了污染环境的废气、废水对测度的相对效率存在误差影响。而现实中的经济活动，在扩大产出时必将会伴随着非期望产出的增加，因此本文对资源型城市TFP的测度将非期望产出加入传统DEA模型。国内外都有学者对非期望产出的处理进行研究，如Kumar等[15]、Oh.D.H[16]将非期望产出作为产出要素引入ML生产率指数，从而实现以最小资源投入带来最大期望产出和最小非期望产出目标；王波等[17]将非期望产出作为投入变量，保持产出不变同时使投入要素和非期望产出同比例下降，但是该模型需要保证投入与非期望产出按相同倍数缩小或增加，与实际生产过程不太相符；许平等[18]也把非期望产出作为投入要素，分别测算径向和非径向DEA模型下决策单元的相对效率。为了更好地反映资源型城市低碳转型的效果，本文以基于方向距离函数的DEA模型与Malmquist-Luenberger(简称ML)指数相结合，测算资源型城市的全要素生产率，从而评价其低碳转型效果。

1.2 方向距离函数

以资源型城市为决策单位构建生产技术前沿，假设有K个资源型城市，每个城市经济生产活动都有M投入(x1，…xn)∈RM，同时得到D种期望产出(y1，…yD)∈RD，P种非期望产出(u1，…uP)∈RP。生产可能集T(x)={(y，p)：x能生产(y，p),x∈RM}，且满足以下三个性质。①期望产出与投入自由处理。若(y，u)∈T(x)，且y’≤y，x’≥x，则(y’，u)∈T(x)。②非期望产出弱处理。非期望产出的减少必然会导致期望产出降低，即(y，u)∈T(x)，且0≤θ≤1，则(θy,θu)∈T(x)。③零结合性。要实现零非期望产出，则期望产出也将减少至零，即(y，u)∈T(x)，且u=0，则y=0。

在以上假设的基础上，方向距离函数可以定义为式(1)。

sup{β:(yt,ut)+β·gt∈Tt(x)}

(1)

式中：gt为方向向量；β为方向性距离函数值，表示期望产出增加的程度和非期望产出减少的程度。

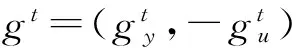
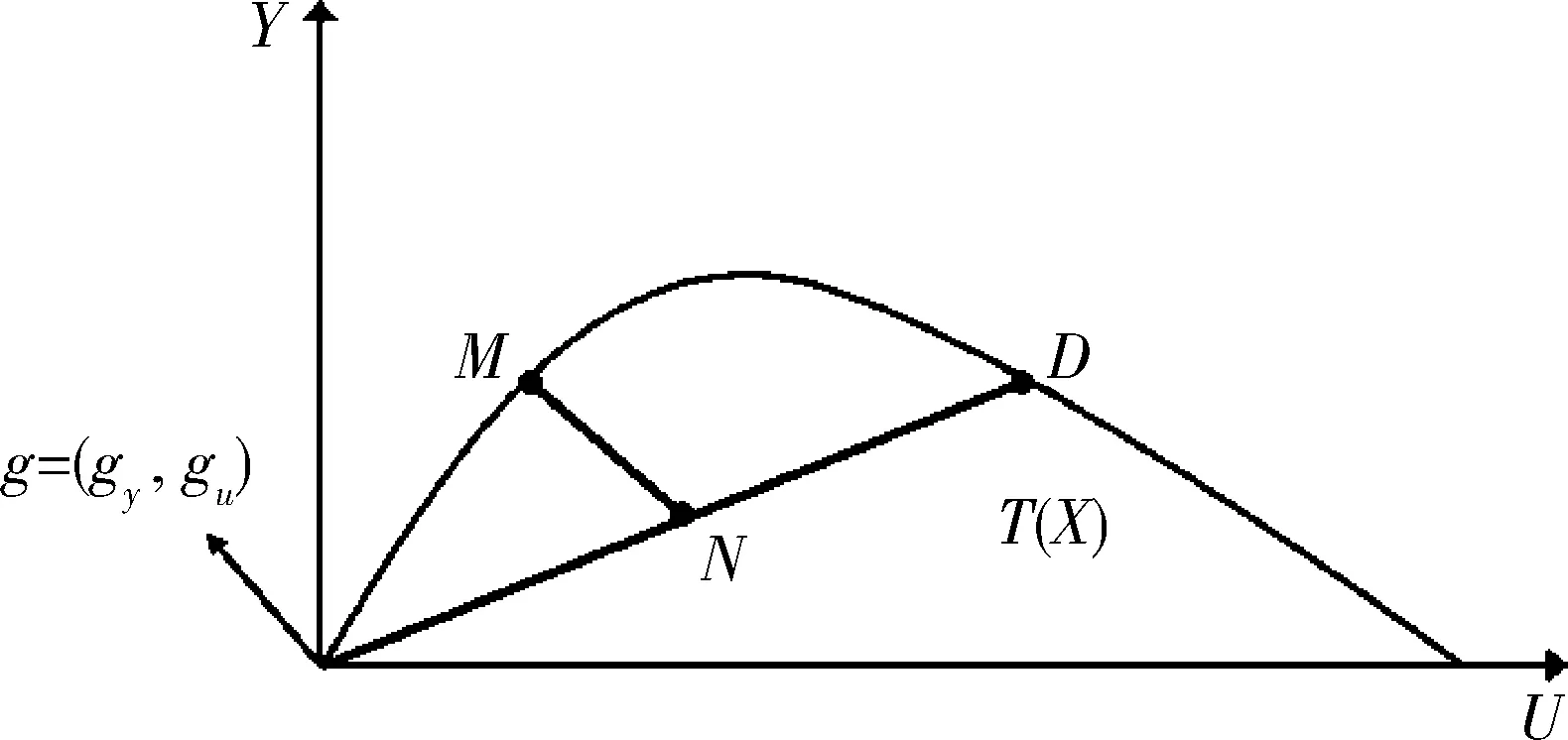
图1 方向距离函数

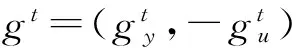
(2)

令gt=(yt,-ut)时，即把期望产出和非期望产出的实际观测值作为方向向量，则第K个DMU在T时期的方向距离函数可以写成如式(3)所示的线性规划形式，式(4)和式(5)分别表示t+1时期技术t期混合方向距离函数和t期技术t+1时期混合方向距离函数。

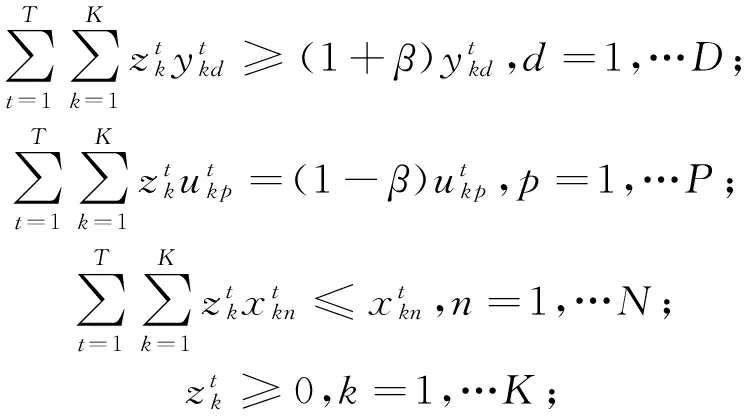
(3)

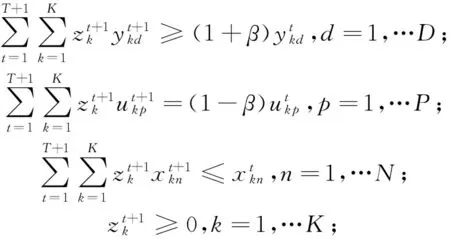
(4)

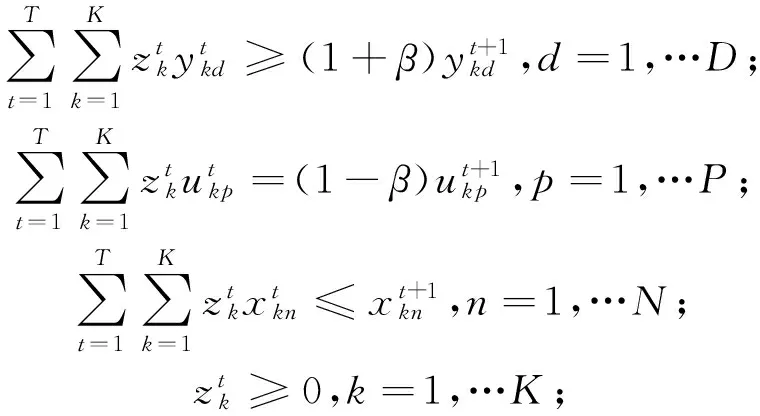
(5)

1.3 ML生产率指数及其分解

根据Chung等[14]提出的ML生产率指数，以每个资源型城市的实际观测值作为方向向量，则t期到t+1期的ML生产率指数可以表示为式(6)，在规模报酬不变条件下，ML生产率指数可以分解为技术效率指数(TCML)(式(7))和技术进步指数(ECML)(式(8))两部分，即ML=TCML×ECML。ML指数测度的是决策单元从t期到t+1期TFP的变化程度，当ML指数>1时,说明TFP有所增加，当ML指数<1时，TFP有所降低，当ML指数=1时，说明TFP没有改变；而ECML测度每个DMU在相邻时期内产出逼近前沿面的程度，当ECML>1时，表示每个DMU在t+1时期更靠近生产前沿面，说明在效率是进步的；TCML指数测度相邻时期内每个生产前沿面移动的距离。当TCML指数>1时，说明技术进步使得非期望产出减少与期望产出增加。

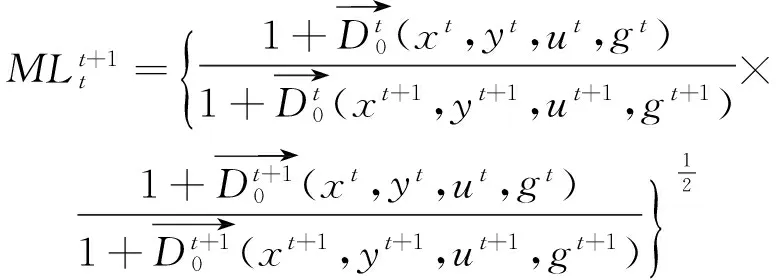
(6)

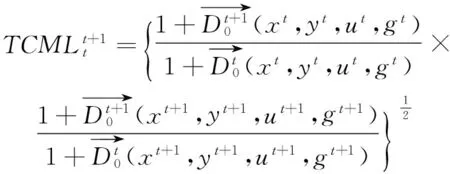
(7)

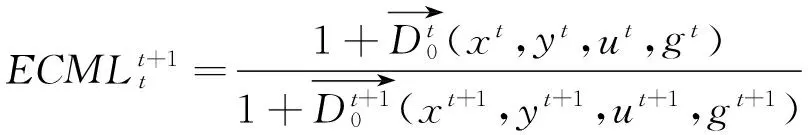
(8)

2 模型结果与分析

2.1 指标与样本的确定

为了对资源型城市低碳转型全要素生产率进行深入探讨，首先需要确定投入产出变量，传统TFP的测度是将劳动力、资本作为投入变量，将GDP作为期望产出变量。为了使测算出的全要素生产率能最佳地反映资源型城市低碳转型效果并综合考虑指标代表性、数据可得性和统计口径一致性，本文选取在岗职工平均人数作为劳动力投入变量，固定资产投资总额作为资本投入变量，全社会用电量作为能源投入变量；选取资源型城市地区生产总值与限额以上工业总产值作为期望产出变量；选取工业SO2排放量、工业废水排放量、工业烟(粉)尘排放量作为非期望产出变量。同时将地区生产总值和限额以上工业总产值按照以2008年为基期的CPI指数进行平减处理，固定资产投资总额按照以2008年为基期的固定资产投资价格指数进行平减处理。

由于转型效果的体现需要一个时间过程，本文拟采用从2008年开始分三批确定的资源枯竭型城市作为测度对象，但是由于第三批与第一批相隔时间太久，导致转型工作存在时间差不利于统一计算，同时考虑数据的可得性，因此本文最终从2008年和2009年确定的两批资源枯竭型城市中选取17个作为低碳转型效果的测度对象。本文所有指标数据均来源于《中国城市统计年鉴》与《中国统计年鉴》。

2.2 资源型城市全要素生产率变化趋势分析

本文计算了2008～2015年我国17个资源型城市的ML指数，表1给出所有资源型城市历年平均ML指数，并将ML指数分解为技术进步变化指数(TCML)和技术效率变化指数(ECML)，图2则是ML指数及其分解部分的波动情况，表2给出了各资源型城市七年平均ML指数及其分解结果。

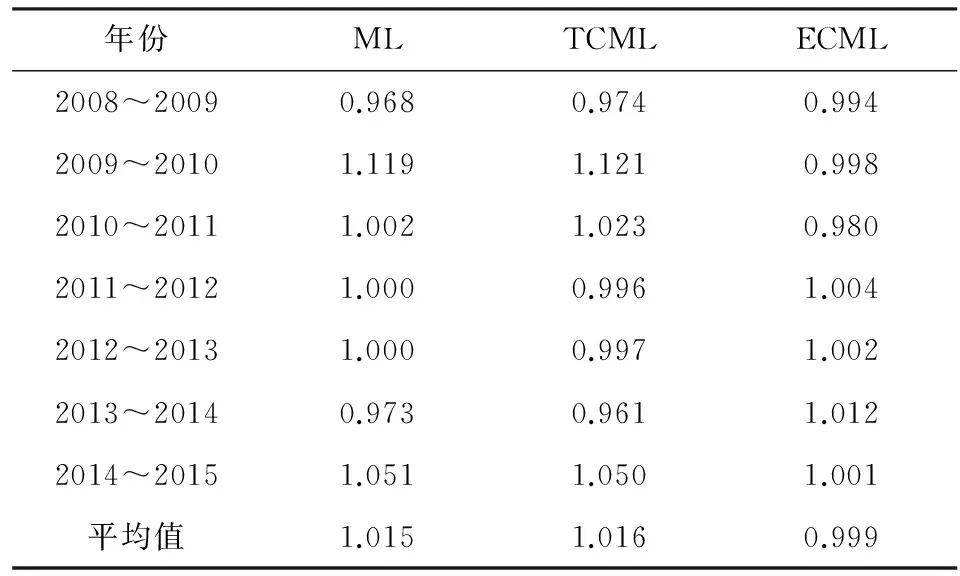
表1 资源型城市历年平均ML指数

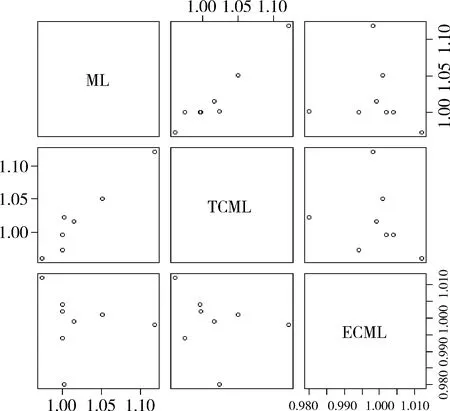
图2 2008～2015年资源型城市平均ML指数及分解指数波动情况

如表1所示，2008～2015年，17个资源型城市包含非期望产出的TFP平均增长率为1.5%，说明资源型城市TFP从总体上来说出现了改善的趋势，即资源型城市低碳转型效果从整体上来说比较好。其中TFP增长的主要原因是技术进步，技术进步指数增加1.6%，而技术效率出现了恶化，从而对TFP的增长存在负作用；且从图2可以看出ML指数与TCML指数的变动呈正相关关系，而ECML指数与TCML指数没有明显的相关关系。这说明资源型城市在低碳技术转型方面的效果比较显著，而城市管理低效率的状态没有得到改善。TFP指数在2009～2013年、2014～2015年这几个阶段都大于1，增长的动力各有不同。在2009～2011年、2014～2015年这两个阶段，全TFP增长的动力主要是技术进步，在2008～2009年、2011～2014年间，TFP增长的关键动力是技术效率有了改善，特别指出的是在2013～2014年间技术效率的改进并没有弥补技术倒退对TFP的影响，从而使全要素生产率指数下降。而在2014～2015年间，技术进步和技术效率的提高共同促进资源型城市全TFP的增长，但前者相对作用更大。因此，TFP增长的动力并不是一成不变，而是技术进步与技术效率相互促进的作用。技术效率指数增加说明城市管理措施的优化和领导决策的正确性，而技术进步指数增加则说明生产技术出现了创新。

从表2可知，在这些城市中，除盘锦、铜陵、枣庄、黄石、铜川、白银外的所有城市，即65%的资源型城市ML指数大于1，说明大部分资源型城市都经历了TFP增加，其中，抚顺、萍乡的TFP增长幅度超过8%；阜新、白山、伊春的增长幅度也较多，均在5%左右，而白银的TFP下降的最多，达到6.7%。从TFP增长的构成来看，除淮北和黄石之外，其他资源型城市的技术效率都保持不变或提高，而盘锦、铜陵、枣庄、黄石、铜川、白银的技术进步指数有所下降。并且可以看出对TFP影响的主要因素是技术进步或技术落后，大部分资源型城市技术效率基本上保持不变，而淮北和黄石的技术效率分别下降1.2%和1.3%，这说明这两个城市的产业管理方法和管理效率有待改进。从城市的角度来看，各个城市都经历了技术效率改善和技术进步，但是存在着较大程度的差异。图3给出了各资源型城市2008～2015年ML增长率的变动情况。从图中可以看出大部分资源型城市的TFP增长率并非一直呈上升趋势，而是处于小范围内的波动，从2008～2009年和2014～2015年两个年度的TFP增长率来看，超过60%的资源型城市TFP增长率是增加的。2009～2010年大部分城市的TFP得到大幅增加，盘锦、枣庄、焦作和石嘴山的TFP有小幅度的下降，即自2008年国家陆续将这些城市确定为资源枯竭型城市以来，各大资源型城市纷纷采取低碳转型，并且短期效果显著，技术效率和技术进步的提高都促使TFP增加，但后者的贡献相对更大。其中， 2010～2011年度的阜新， 2012～2013年度的铜陵、2013～2014年度的铜川的ML指数都有大幅下降，

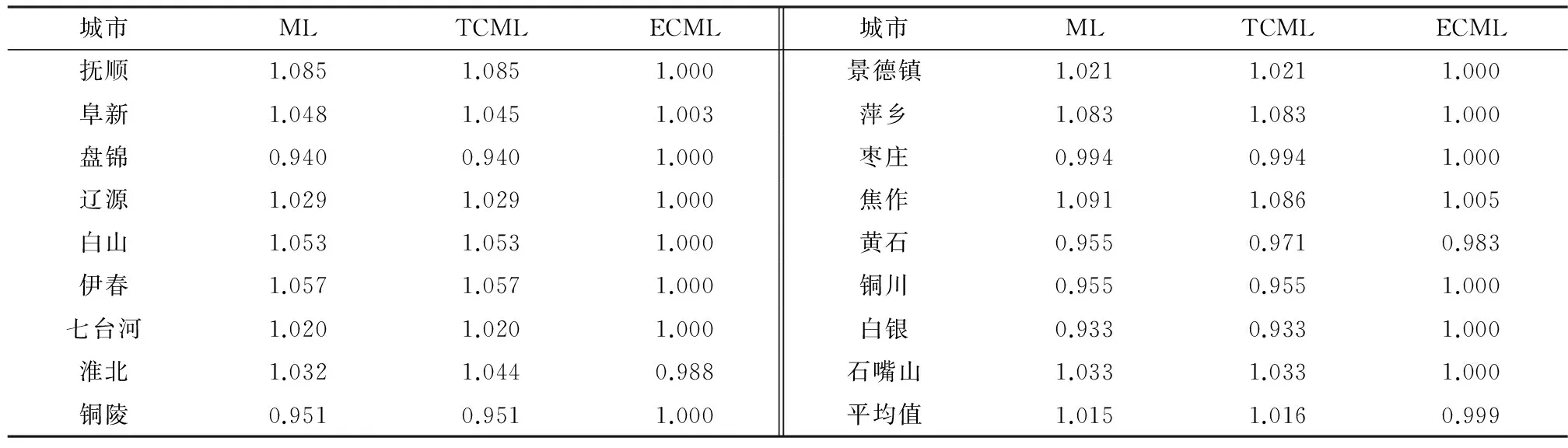
表2 资源型城市平均ML指数及其分解

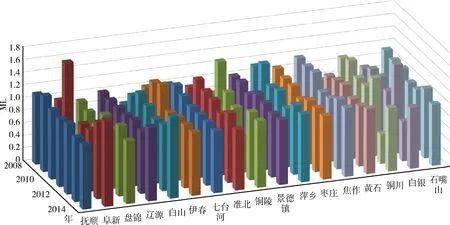
图3 2008～2015年资源型城市ML指数波动情况

这主要是由于资源型城市在进行低碳转型过程中的一些措施导致的，比如2013年铜川市对污染严重的水泥企业实施整体关闭拆除，导致工业增加值大幅减少。铜川市的ML指数在2013年前是逐步增长的，这主要得益于铜川市从产业低碳化、可再生能源利用规模化、污染物减排化等方面进行的低碳转型。

2.3 资源型城市TFP变动区域差异分析

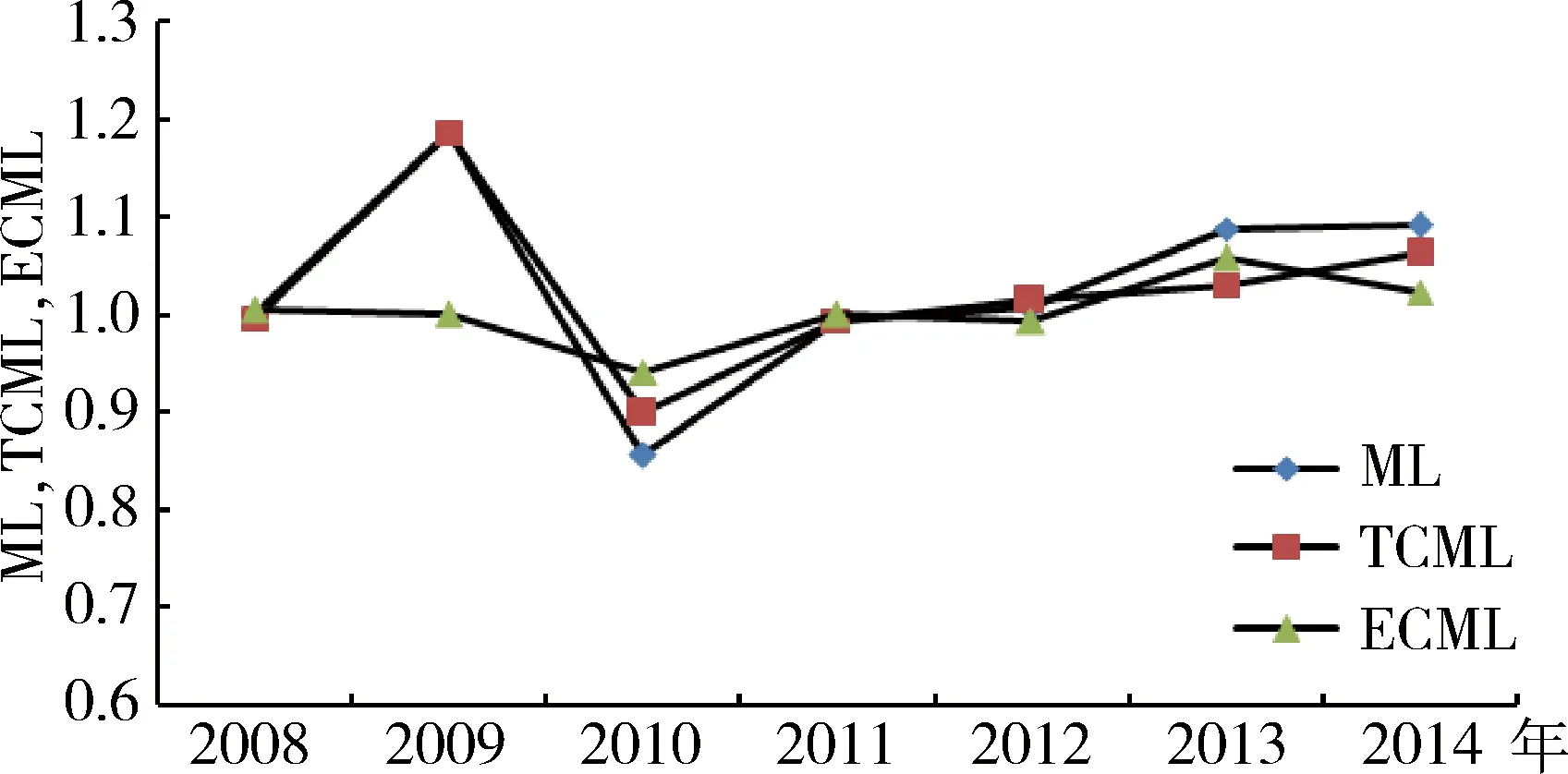
图4 东部资源型城市ML指数及分解指数波动情况

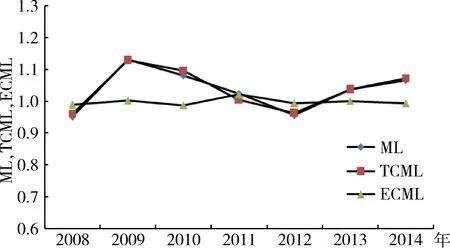
图5 中部资源型城市ML指数及分解指数波动情况

图6 西部资源型城市ML指数及分解指数波动情况

由于选取的资源型城市处于我国东部、中部、西部三个地区，不同地区的生产效率和生产技术都存在明显的差异，实施低碳转型的力度和措施也存在严重的不平衡，因此本文按照地区分别对资源型城市的全要素生产率增长率进行差异分析。图4～6分别给出了2008～2015年东部、中部、西部资源型城市ML指数和分解指数的波动情况。从平均值角度，东部和中部的TFP指数均大于1，并且中部资源型城市的TFP最高为2.9%，而西部的增长率为-2.6%，这主要是由投入产出技术的差异导致的。在2009～2010年东部地区TFP增长率达到18.6%，中部地区TFP也达到13.1%，这说明资源型城市低碳转型的短期效果十分显著。从TFP的构成来看，东部和中部的投入产出技术有所改进，中部地区的技术进步指数增长幅度达到3.1%，而西部的技术出现退化，增长率为-2.6%。从均值角度，三个地区的技术效率指数均没有太大的变化，仅东部地区增长0.1%。从东部、中部、西部历年平均ML指数来看，2008～2010年、2013～2015年这两个时期，东部、中部、西部资源型城市的TFP指数整体呈上升趋势，增长的主要动力却有所不同。

2.4 资源型城市TFP变动资源差异分析

在本文所选取的资源型城市中，由于不同城市原开采方式、资源属性和资源利用程度等方面存在差异，使得相应资源型城市低碳转型难易程度存在明显的区别，因此，本文计算出不同资源类别城市的全要素生产率增长率及其分解情况。本文涉及到的类别有综合型、煤炭型、金属型和其他类型，其中综合资源型城市4个，煤炭资源型城市7个，金属资源型城市3个，其他资源型城市3个。图7给出了2008～2015年不同类别资源型城市的平均ML指数及其分解情况。从图7可以看出，除了金属型城市的平均TFP增长率有点降低之外，其他类型资源型城市的TFP都呈现出不同程度的增长，其中增长率最快的是综合型城市，年均增加3.9%，主要的增长动力是技术进步，这说明综合型城市技术创新对促进城市低碳转型效果更加显著。而煤炭资源型城市在经过低碳转型后，TFP平均增长率也达到3.8%。

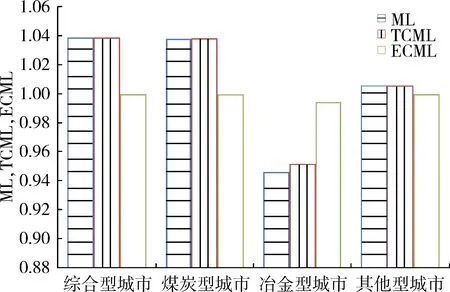
图7 不同类别资源型城市平均ML指数及其分解

3 结论与建议

本文以17个资源型城市为例，采用2008～2015年的面板数据，选取基于方向性距离函数的DEA模型测算城市的TFP，用考虑非期望产出的全TFP测度模型来对资源型城市低碳转型效果进行评价，得出如下主要结论。

1) 从平均值角度，资源型城市TFP呈现增长趋势，生产率增长的动力主要源于技术的进步，反映了当前资源型城市在低碳技术的运用和大规模机器设备更新下，以技术创新推动经济增长的低碳发展模式，因此资源型城市在低碳技术转型方面效果显著；而技术效率的变动呈现小幅度的下降，对生产率的增加产生反向作用，意味着资源型城市在管理效率转型方面还有待改进。

2) 不同资源型城市在不同年度经历了差异化的TFP增长。各资源型城市的TFP在增长和下降中不断波动，这说明在低碳转型过程中，资源型城市降低产能，关闭污染型企业，大量资金投入技术创新，必然会面临一定数量的市场投入只能带来相对较低水平的产出，从而使得TFP增长率降低。但从整个时期来看，资源型城市在产业低碳化、可再生能源利用规模化、污染物减排化等方面做出的低碳转型，最终使大部分资源型城市的TFP呈现增长的趋势。

3) 资源型城市TFP增长率在不同地区之间和不同资源类别之间都存在差异，即资源型城市低碳转型效果的差异化不仅存在于地区之间，还存在不同资源类别之间。东部和中部地区资源型城市的TFP增长率成上升趋势，西部地区的TFP增长率稍有下降；从资源类别来看，除金属类资源型城市，其他类别资源型城市TFP增长都呈上升趋势，其中TFP增长幅度最大的是综合型资源型城市。近几年，煤炭资源型城市应该是转型力度最大的资源型城市，主要的低碳转型措施包括发展生态文化旅游业、以创新为内生动力培育新兴产业、加大低碳技术和清洁能源研发开发与推广等。因此，煤炭资源型城市的TFP增长幅度也比较大，排名第二。同地区之间和不同资源类别之间资源型城市TFP增长率差异化的关键是原因是各城市技术进步本身存在差别。

根据前文对我国资源型城市低碳转型效果的现状分析，本文从技术效率和技术进步两方面提出对策建议。第一，加快促进产业结构升级，提高投入要素的使用效率。技术效率变化指数是衡量投入要素是否得到有效地利用，从而得到最优期望产出和最少非期望产出。对于技术效率指数下降的中部地区资源城市和金属型资源城市，要成功实现低碳转型，需要更加科学有效地确定投入资源规模和比例，并配备合理的控制监督调整投入生产过程，科学调整产业结构，合理配置资源，才能实现产出的最优化，进而提高资源型城市技术效率，实现减排和改善环境目的。第二，加大低碳技术研发和推广力度，促进新兴产业的快速发展。目前，我国资源型城市的技术发展有所进步，是TFP增长的关键动力，因此，技术进步对资源型城市低碳转型有重要作用，技术产业的发展使资源型城市主导产业由资源依赖型向技术创新型转变。因此，各资源型城市应该大力培养高新技术人才，努力推广低碳技术，将低碳技术运用于传统产业的升级和新兴产业的发展。此外，要推广清洁能源和可再生能源的使用，促进新能源产业的发展，这将有利于产业结构的调整和促进节能目标的实现，进而提高资源型城市的低碳经济发展。

[1] 辛玲.低碳城市评价指标体系的构建[J].决策与参考,2011(7):78-80.

[2] 杨波.资源型城市转型系统评价探析——以我国黄金生产大市招远为例[J].东岳论丛,2013,34(12):174-178.

[3] 袁晓玲,雷厉,仲云云.低碳经济评价指标体系构建及实证分析[J].城市问题,2013(1):56-61.

[4] 李友俊.资源型城市低碳经济发展水平评价实证研究——以大庆市为例[J].齐齐哈尔大学学报:自然科学版,2014,30(1):75-78.

[5] 赵海云,李仲学,张以诚.矿业城市的可持续发展指标体系研究和可持续发展水平评价[J].中国矿业,2004,13(12):18-23.

[6] 姜传军,吕洁华.林业资源型城市经济转型评价指标体系研究[J].林业经济,2008(11):61-63.

[7] 李晓燕.基于模糊层次分析法的省区低碳经济评价探索[J].华东经济管理,2010,24(2):24-28.

[8] 王小李,谷建龙.基于可变模糊分析的省区低碳经济评价体系探索[J].生态经济,2011(2):24-28.

[9] 安果,李青.城市低碳发展的熵值——灰色系统评判模型[J].统计与决策,2011(19):26-30.

[10] 马丽,黄凤,贾利,我国林业资源型城市转型评价标准与实证研究——以伊春市为例[J].林业经济,2014(6):48-51.

[11] 王学军,侯睿,王玲.基于TOPSIS法的资源型城市低碳转型评价体系研究——以焦作市为例[J].生态经济,2015(11):42-46.

[12] 张荣光.基于熵权——TOPSIS法的资源型城市低碳转型效率研究——以攀枝花市为例[J].学海,2016(4):158-162.

[13] Pittman R W.Multilateral productivity comparisons with undesirable outputs[J].Economic Journal,1983,93(4):883-891.

[14] Chung Y H,Färe R．Grosskopf S.Productivity and undesirable outputs:A directional distance function approach[J].Journal of Environmental Management,1997,51(3):229-240．

[15] Kumar S,Russell R.Technology change,technological catch up,and capital deepening:relative contributions to growth and convergence[J].The American Economic Review,2002,92(3):527-548．

[16] Oh D H.A metafrontier approach for measuring an environmentally sensitive productivity growth index[J].Energy Economics,2010,32(1):146-157．

[17] 王波,张群,王飞.考虑环境因素的企业DEA有效性分析[J].控制与决策,2002,17(1):24-28.

[18] 许平,孙玉华.非期望产出的DEA效率评价[J].经济数学,2014,31(1):90-93.