基于SCADA数据的风电机组关键载荷预测

周士栋，薛　扬，马晓晶，王文卓



基于SCADA数据的风电机组关键载荷预测

周士栋，薛扬，马晓晶，王文卓

（中国电力科学研究院有限公司新能源与储能运行控制国家重点实验室，北京 100192）

风电机组关键位置载荷预测对风电机组安全、经济运行具有重要意义。通过建立SCADA数据与载荷间的近似关系对风电机组关键位置载荷进行预测。采用BP神经网络建立SCADA数据和载荷的关系模型，利用SCADA数据与载荷间的相关性来筛选模型输入参量，采用试错法确定BP神经网络的层数与神经元数量。针对某2.5 MW风电机组的7处关键位置进行了载荷实测。研究表明，在不采用风速作为输入参量的情况下，模型的预测结果与实测结果具有良好的一致性，相对误差的均值在1.28%到15.6%之间，决定系数2在0.951到0.882之间；与试错法选择输入参量相比，基于相关性计算的输入参量选择方法能够更高效地筛选出更多恰当的SCADA参量，从而进一步提高预测准确度。因此，基于BP神经网络建立SCADA数据与载荷的近似关系可作为风电机组关键位置载荷预测评估的有效手段。

风电机组；模型；神经网络；SCADA数据；参数筛选；疲劳等效载荷；载荷预测

0 引 言

近年来，随着风电场装机容量的不断增大，风电场安全性与经济性间的矛盾也越发突出。一方面是大容量风电机组的复杂受载给结构安全带来的巨大挑战[1]，另一方面是高昂的风电场运维费用[2]。为了加强风电机组安全保障、合理规划风电场运维计划，有必要对风电机组关键位置的受载情况进行监测评估。

风力发电机组的载荷受流固耦合及控制系统导致的气动伺服因素的影响。风力发电机组载荷的来源主要包括：空气动力载荷、重力载荷、惯性载荷、运行载荷、其他载荷。最常用的载荷监测手段是通过粘贴应变片实现，由于该方法人力物力耗费较大、应变片自身寿命有限等原因并不适用于风电机组载荷的长期监测。以GH bladed为代表的风机性能及载荷计算仿真软件[3-6]，由于无法实时得到全面的风况信息，因此也不适用于现场载荷的评估。因此，有必要发展一种经济、可行的风电机组载荷预测评估方法。

风电机组复杂的受载状态以及载荷间的耦合关系增加了风电机组载荷预测的困难，如回归分析、插值等传统分析方法很难得到高准确度的经验或半经验预测公式。风电机组普遍装有SCADA（数据采集与监视控制）系统，该系统记录了机组大量的运行数据。通过对运行数据的挖掘处理，建立关键运行参数与载荷间的近似关系，成为风电机组载荷预测研究方向。国内外相关研究人员[7-10]通过人工神经网络建立SCADA数据与载荷间的关系模型实现了机组的载荷预测。然而，这些研究仅预测了机组部分位置的载荷，未对风电场运维中各关键位置载荷进行全面研究。由于风电机组属于多能量耦合系统，运行状态波动大，结构复杂，不同位置载荷特性不一，能否利用有限的SCADA数据对各关键位置载荷进行全面准确地预测尚需研究验证。其次，在建立关系模型时，输入参量的选择往往依靠试错法，通过对若干组SCADA数据参数组合的预测结果对比，选择一组最优的参数组合。这种方法效率低，用来试错比较的参数种类及其组合往往不足，因此无法确定在已有的SCADA数据里是否有更优的参数组合。

本文选取某2.5 MW双馈型风电机组，针对IEC标准强制要求测量的7个关键位置进行了载荷实测。利用实测数据，验证了基于风机自身SCADA数据的载荷预测方法能否对机组不同位置处特性不一的载荷进行全面、准确地预测。基于相关性计算，本文针对不同位置的载荷筛选了相应的输入参数，验证了基于相关性的参数选择方法的适用性。除此之外，尽管风是风电机组动态载荷的主要来源，但考虑到风电场很少立有测风塔且正常发电时机舱风速计受旋转叶片干扰明显，因此本文在进行载荷预测舍弃了风速，验证了在“无风”可用的情况下基于SCADA数据的载荷预测模型的准确性。

风电机组载荷来源广、受载复杂且受控制策略影响明显，风电机组运行参量与载荷相关但关系模糊。人工神经网络作为非线性、自适应信息处理系统能够有效处理机理较模糊或复杂非线性问题，且基于误差逆向传播算法的神经网络（BP神经网络）应用广泛且成熟[11-15]。因此，本文尝试采用BP神经网络建立SCADA数据与载荷间的关系模型。

1 基于SCADA数据的载荷预测模型

基于SCADA数据，利用神经网络构建的风电机组载荷预测模型的框架结构如图1所示。

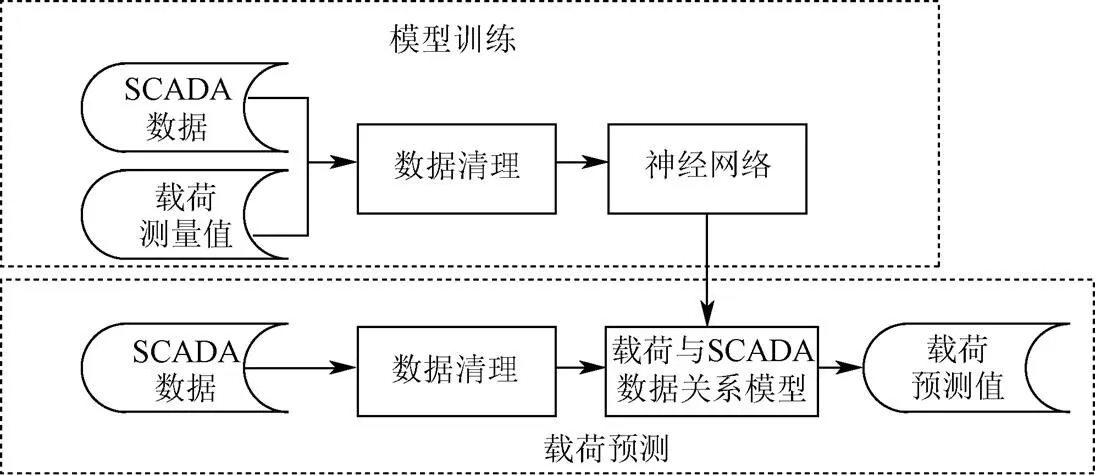
图1 载荷预测模型框架

1.1 输入数据

输入数据包括SCADA数据和载荷测量值2类。SCADA数据直接通过风电机组控制系统收集得到，载荷数据通过粘贴在各关键位置处的应变片测量得到。

1.2 数据清洗

正常发电状态时风电机组载荷受周围障碍物（其他风电机组）影响明显。根据来流是否受障碍物影响可分为自由流和非自由流（受尾流影响）。本文仅就正常发电时自由流条件下的风电机组载荷进行预测。

根据数据的有效性[16]，就正常发电时自由流条件下采集的数据进行清洗。所要清洗的数据包括：1）非正常发电状态下的数据，2）受尾流影响的数据，3）信息不完整的数据，4）数值大小超出物理极限的，5）反常数据。

1.3 神经网络

神经网络由大量的节点（神经元）相互联接构成，各节点将输入信号的加权和作为输入传递给激励函数，激励函数的计算结果作为本节点的输出。一个完整的神经网络包括输入层、隐藏层和输出层。BP神经网络是基于误差逆向传播算法的前馈神经网络，它建立在梯度下降法基础上。其中，输入信号按单方向由输入层经隐含层传至输出层，信号不形成回路。信号在传递过程中权值保持不变，每一层神经元的状态只影响下一层神经元的状态。输出值与期望值间的误差由输出层开始逐层向后传播。在误差反向传播过程中，网络的权值根据误差反馈进行调节。通过权值的不断修正使网络的实际输出值不断接近期望值，直至满足预先设定的误差要求。

1.4 模型的训练及预测

在完成数据的清洗后，对SCADA数据与风电机组载荷进行相关性分析，筛选出与载荷变化相关的SCADA数据参量。基于实测数据，利用神经网络建立载荷与SCADA数据关系模型。利用建立的关系模型和机组SCADA数据可以进行载荷的预测。

2 风电机组关键位置载荷实测

本文选取了某2.5 MW双馈型风电机组开展载荷实测工作。所选风电机组的主要参数为：水平轴双馈型机组、轮毂高度90 m、风轮直径121 m、额定风速10.2 m/s、额定功率2 500 kW。所选风电机组位于河北省张家口市张北风电试验基地，测试严格按照IEC 61400－1[17]和IEC 61400－13[18]标准开展。测试系统采用基于CAN BUS通信协议的风电机组载荷测试系统[19-20]。该系统包括主系统、气象数据采集系统、轮毂数据采集系统、塔顶数据采集系统、电池系统以及UPS（不间断电源）系统6个部分组成，如图2所示。

图2 风电机组载荷测试系统

测试系统收集的SCADA信号包括：1）机舱前后加速度，2）机舱左右加速度，3）有功功率，4）齿轮箱油温，5）刹车液压，6）叶片桨距角，7）叶轮转速，8）发电机扭矩，9）偏航方位角，10）偏航误差。

气象量包括：1）风速，2）风向，3）温度，4）气压。

测量的关键位置载荷包括：1）叶片的摆振弯矩，2）叶片的挥舞弯矩，3）塔顶俯仰弯矩，4）塔顶倾覆弯矩，5）塔顶扭矩，6）塔底俯仰弯矩，7）塔底倾覆弯矩。

测试从2016年11月18日开始，到2017年3月20日终止。

3 载荷预测模型的建立与应用

本节我们基于实测数据，利用BP神经网络建立SCADA数据与载荷间的关系模型。通过比较预测结果与实测结果验证了基于SCADA数据的风电机组载荷预测方法的适用性及有效性。

3.1 数据库

本研究收集了自2016年11月18日至2017年3月20日间的测试数据。训练数据选择2016年11月18日到2017年2月20日期间的数据，预测数据为2017年2月20日到2017年3月20日期间的数据。载荷预测模型使用的数据为10 min时间序列数据的统计值（最大值、最小值、平均值、标准差）。按照1.2节所述，在原始数据中剔除如下数据：1）启、停机等瞬态工况及未并网发电下的数据；2）不在可用扇区内的数据；3）应变片等测量硬件故障状态下采集的数据；4）10 min周期内采集不完整的数据；5）风电机组内部电磁干扰导致的反常数据。剔除后的有效数据量如表1所示。以叶片的摆振弯矩的均值为例，清洗前后的数据对比如图3所示。

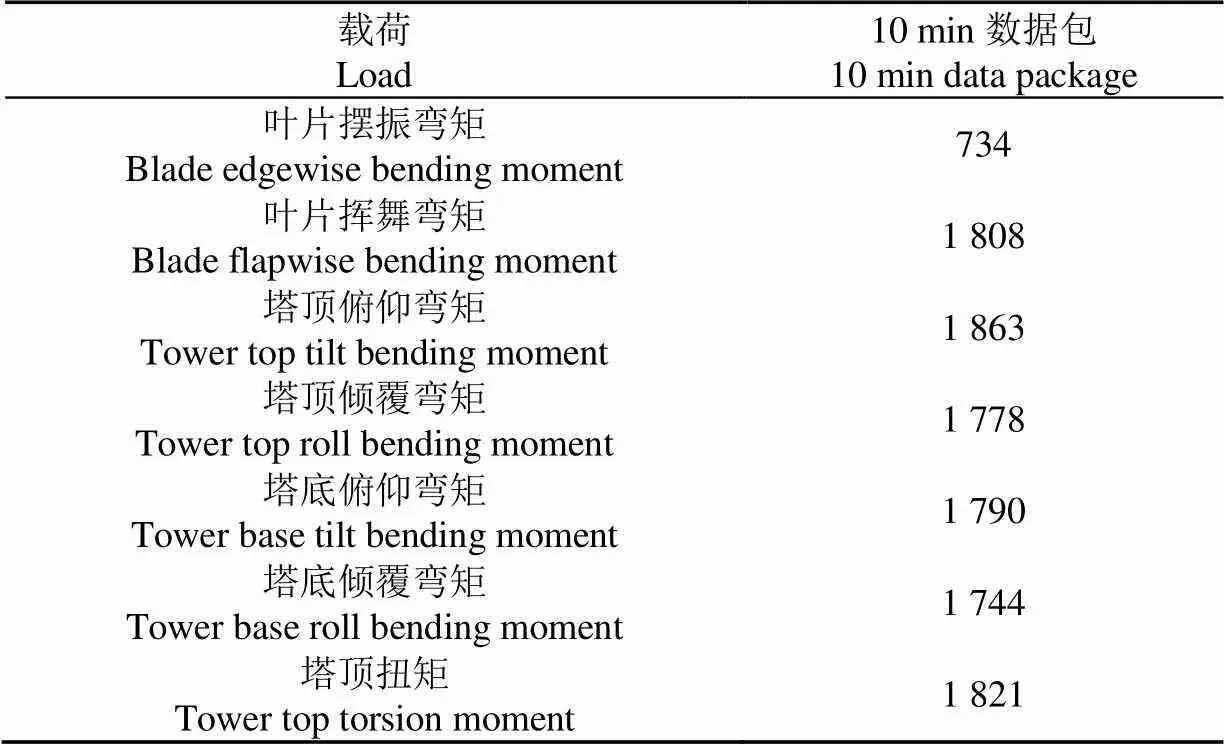
表1 有效数据量

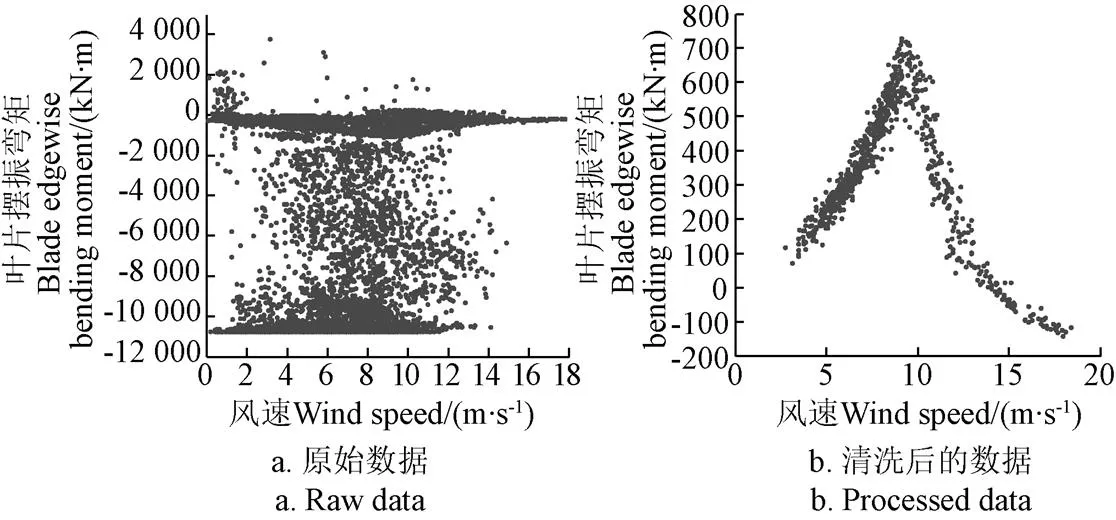
图3 叶片摆振弯矩均值

3.2 疲劳等效载荷

由于风电机组所承受的载荷主要是随时间变化的动态随机载荷，结构因此而产生动应力，引起疲劳损伤。因此，本文选取疲劳等效载荷作为风电机组载荷的评估指标。

疲劳等效载荷是一个概括性的载荷，是指以给定的时间范围（10 min）和频率（1 Hz）确定的总的循环次数施加这个载荷时，它所造成的累积疲劳损伤与给定的时间范围（10 min）内实际动态载荷对结构部件造成的累积疲劳损伤相同。疲劳等效载荷的定义为

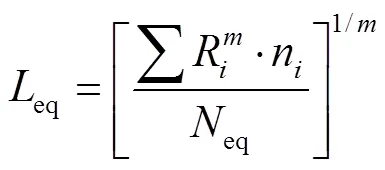
式中eq为等效载荷，R为第级的载荷幅值，n为第级的载荷循环次数，eq为等效载荷循环次数，为材料S-N曲线的斜率。R和n通过雨流计数的得到，eq的大小为600，的大小按照IEC标准[18]建议取8。

按照疲劳等效载荷的定义，将关键位置处实测得到的10 min时间序列弯（扭）矩转化为疲劳等效弯矩。图4以叶片摆振为例展示了转化后的等效疲劳载荷。在下文中，弯（扭）矩或等效弯（扭）矩均表示疲劳等效弯（扭）矩。

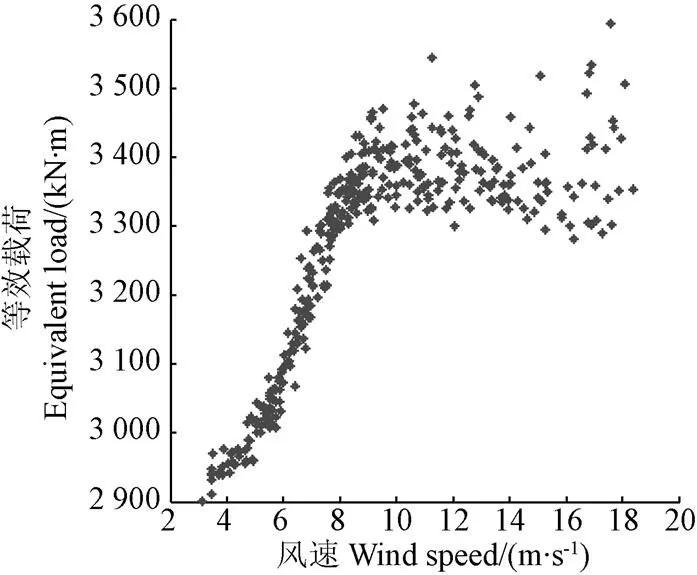
图4 等效疲劳载荷

3.3 BP神经网络

BP神经网络结构的选择至今尚无统一而完整的理论指导，一般只能由经验选定[21-25]。本研究中，BP神经网络的层数及隐含层神经元数量通过试错法确定。其中，隐含层内神经元数量按经验公式（2）初选[26]

式中为隐含层内神经元数量，为输入层单元数，为输出层单元数，为0到10之间的常数。以叶片摆振为例，输入层单元数为11，输出层单元数1，图5给出了不同隐含层和神经元数量组合下预测值与实测值间的相对误差的均值。由图5可见，1层隐含层较2、3层隐含层有更好的预测效果。当隐含层为1层、隐含层内神经元数量为6时准确度最高。在预测风电机组其余位置载荷时，隐含层数量统一设为1层，隐含层内的神经元数量通过试错法确定最优值。

学习率的选择受计算速度与网络收敛的双重限制。当增大学习率时可以提高计算速度，但也可能导致结果发散。Kung等[27]提出的学习率为

式中h为神经元数量。以叶片摆振为例，当隐含层神经元数量为6时学习率为0.286。为保证计算收敛，保守起见本文采用的学习率统一设置为0.2。考虑到工程应用的要求，本文认为当误差为0.01已足够理想，因此目标误差设为0.01；同时兼顾计算速度，最大训练次数设为1 000。BP神经网络算法通过商用软件RapidMiner实现。

3.4 参量选择

训练参数的选择对神经网络模型的准确性有着重要影响，为准确建立风电机组不同位置处的疲劳等效载荷与SCADA数据间的关系模型，我们采用皮尔逊相关系数分析了不同SCADA信号与疲劳等效载荷间的相关性。皮尔逊相关系数的定义为

式中Cov(,)为变量和间的协方差；为变量的标准差；为变量的标准差。

按照相关系数法理论[28]，当2个物理量之间的相关系数值在0～0.09之间时，认为二者之间没有相关性；当相关系数绝对值在0.09～0.3之间时，表示二者之间弱相关；当二者之间的相关系数绝对值在0.3～0.5之间时，表明二者是中等相关；当相关系数绝对值在0.5～1之间时，表明二者之间是强相关的。选取相关系数绝对值在0.3以上的参量作为输入参量。

以塔底等效俯仰弯矩为例，所选SCADA参量及相应的相关性大小如表2所示。为验证基于相关性计算的参数选择方法的有效性，比较了2组输入参数下的预测结果。Obdam等[10]在预测风电机组塔底俯仰弯矩时，利用试错法确定的模型输入参量为轮毂转速的均值和标准差、叶片桨角的均值和标准差、功率的均值和标准差。2组参数对应的预测结果如图6所示。对比可见，按照Obdam输入参量得到预测结果较本文结果更为离散、误差更大。由此可见，基于试错法选择的输入参量并非最优选择。因此为了达到更好的预测准确度，有必要采用更多的SCADA数据作为输入参量，此时基于相关性计算的参数选择方法较试错法效率更高，更适用于参数组合较多的情况。

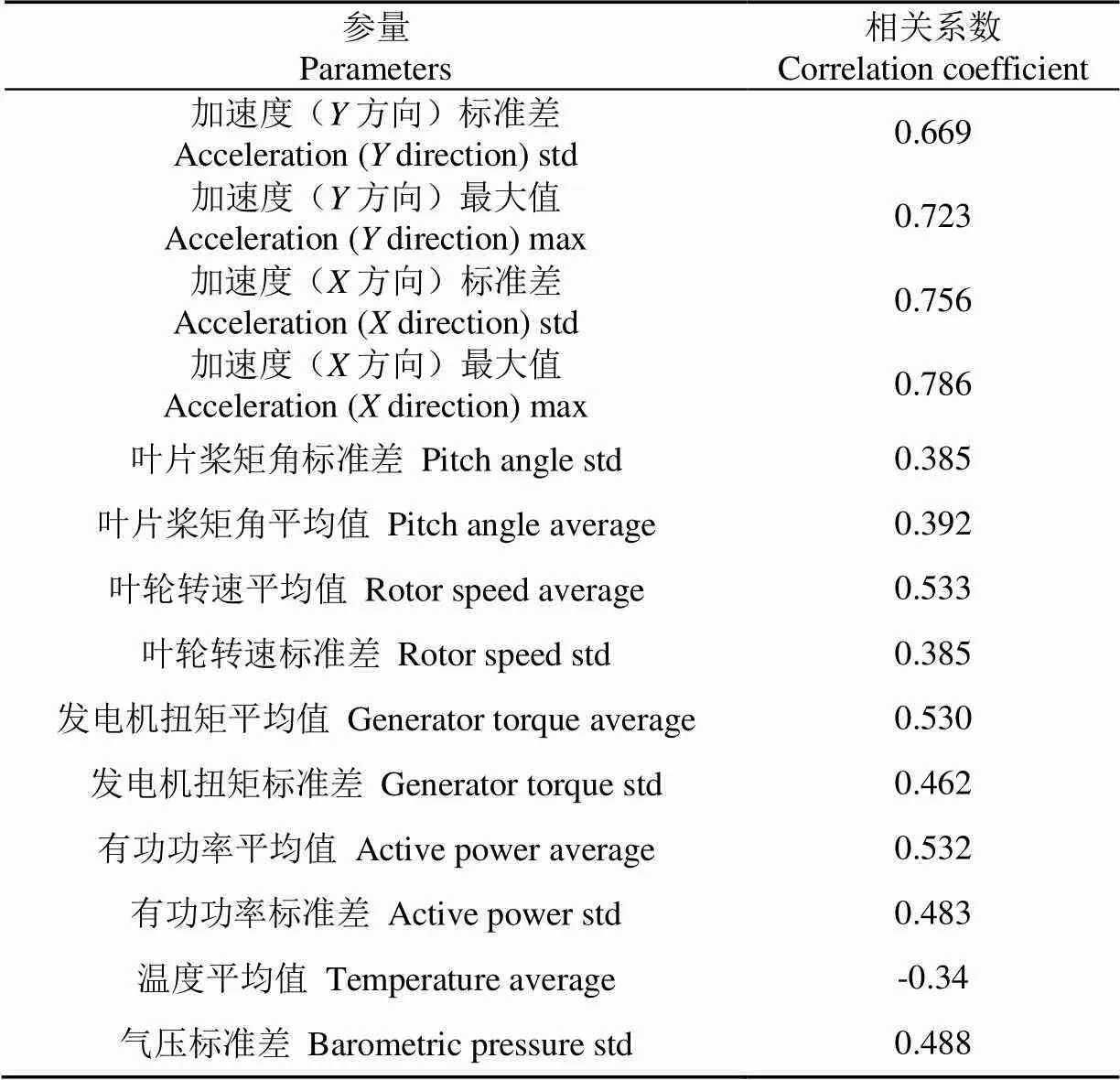
表2 塔底俯仰弯矩与输入参量间的相关性

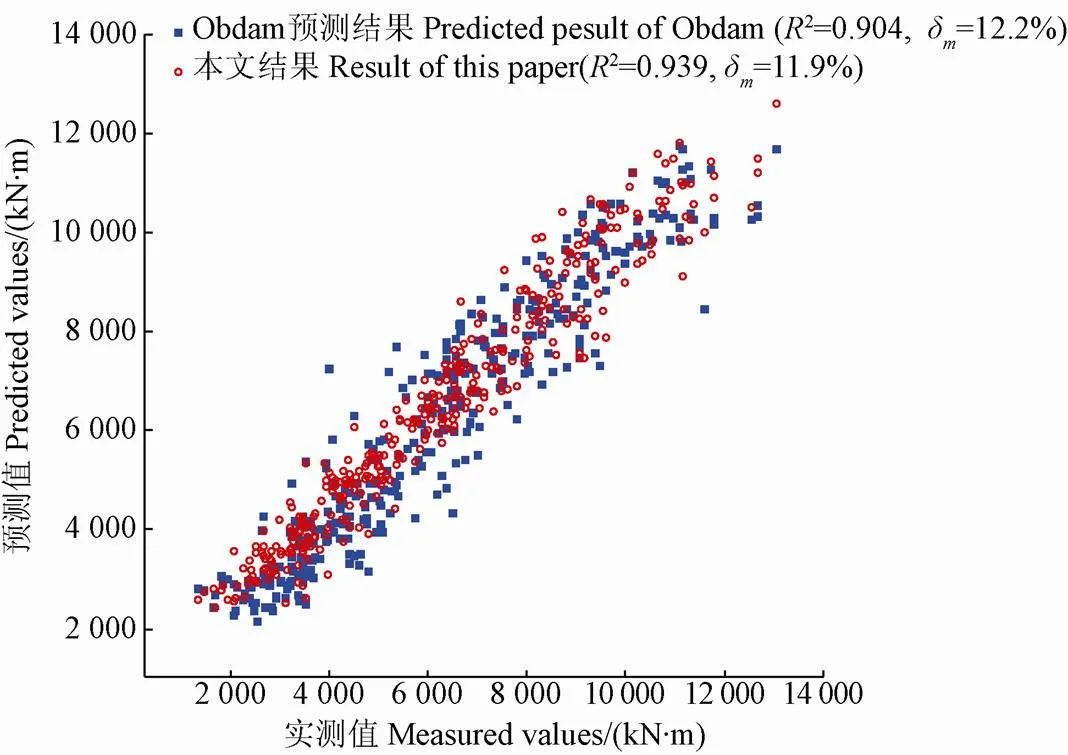
图6 预测结果对比

针对其余位置载荷，基于相关性计算所选的SCADA参量如表3所示。

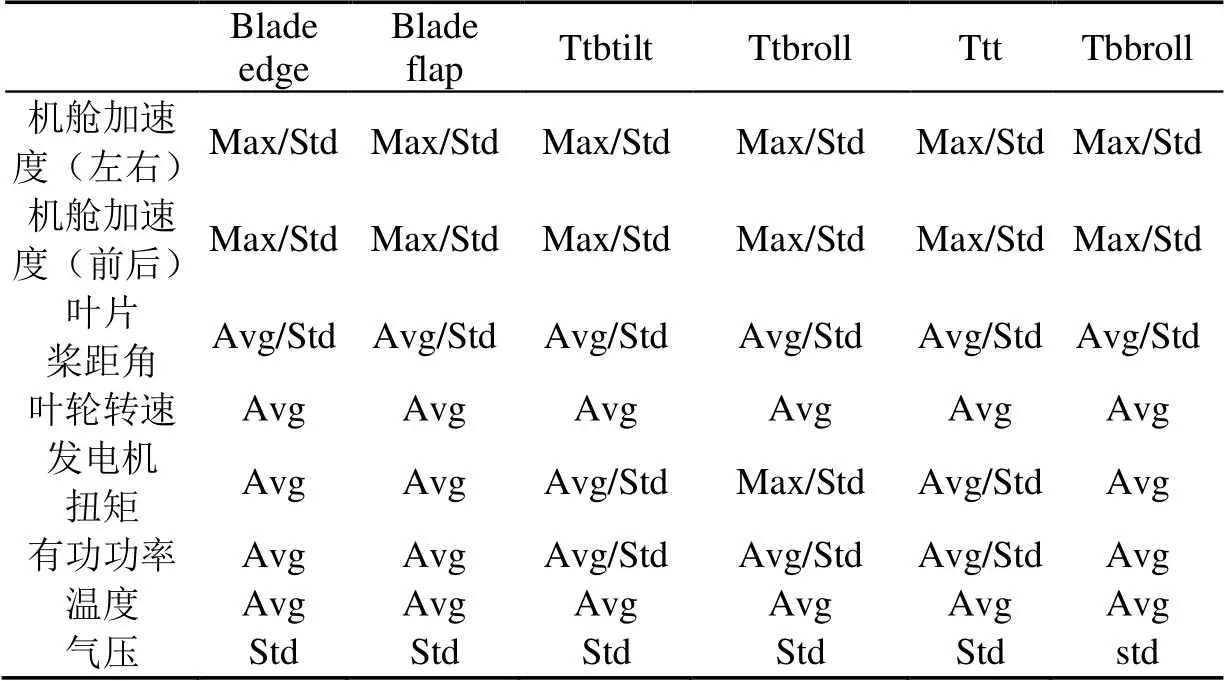
表3 所选SCADA信号参量

注：Blade edge为叶片摆振弯矩，Blade flap为叶片挥舞弯矩，Ttbtilt为塔顶俯仰弯矩，Ttbroll为塔顶倾覆弯矩，Ttt塔顶扭矩，Tbbroll为塔底倾覆弯矩，Avg为平均值，Max为最大值，Std为标准差。

Note: Blade edge represent blade edgewise bending moment. Blade flap represent blade flapwise bending moment. Ttbtilt represent tower top tilt bending moment. Ttbroll represent tower top roll bending moment. Tbbtilt represent tower base tilt bending moment. Tbbroll represent tower base roll bending moment. Ttt represent tower top torsion moment. Max is an abbreviation for maximum. Min is an abbreviation for minimum. Std is an abbreviation for standard deviation. Avg is an abbreviation for average.

在选取参量时，当参量的10 min统计最大值、最小值和均值的相关系数绝对值相当时选取平均值；当统计最大值、最小值相关系数值绝对值大小相当时，选取最大值。除此之外，考虑到相同风速下温度与气压的变化会改变空气密度，进而影响风电机组载荷大小，因此选取气压平均值和温度标准差作为输入参量。

3.5 模型预测结果

本节基于所选SCADA参量及处理后的数据，针对不同位置处的载荷，对神经网络模型分别进行训练。数据库中，选取80%的数据量作为训练数据来建立SCADA数据与载荷间的关系模型，另外20%作为检验数据来验证模型的准确性。

参照相关研究[7-10]中准确性度量指标，本研究使用决定系数2和相对误差均值δ来衡量模型的准确性，这2个指标的定义如式（5）、式（6）所示。

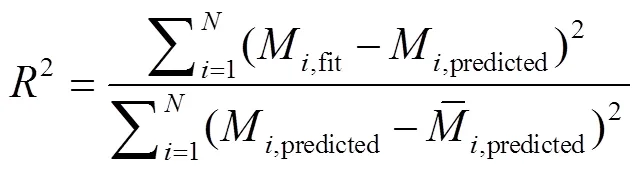
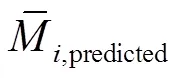
各关键位置处等效载荷的预测结果与实测结果的对比如图7所示。

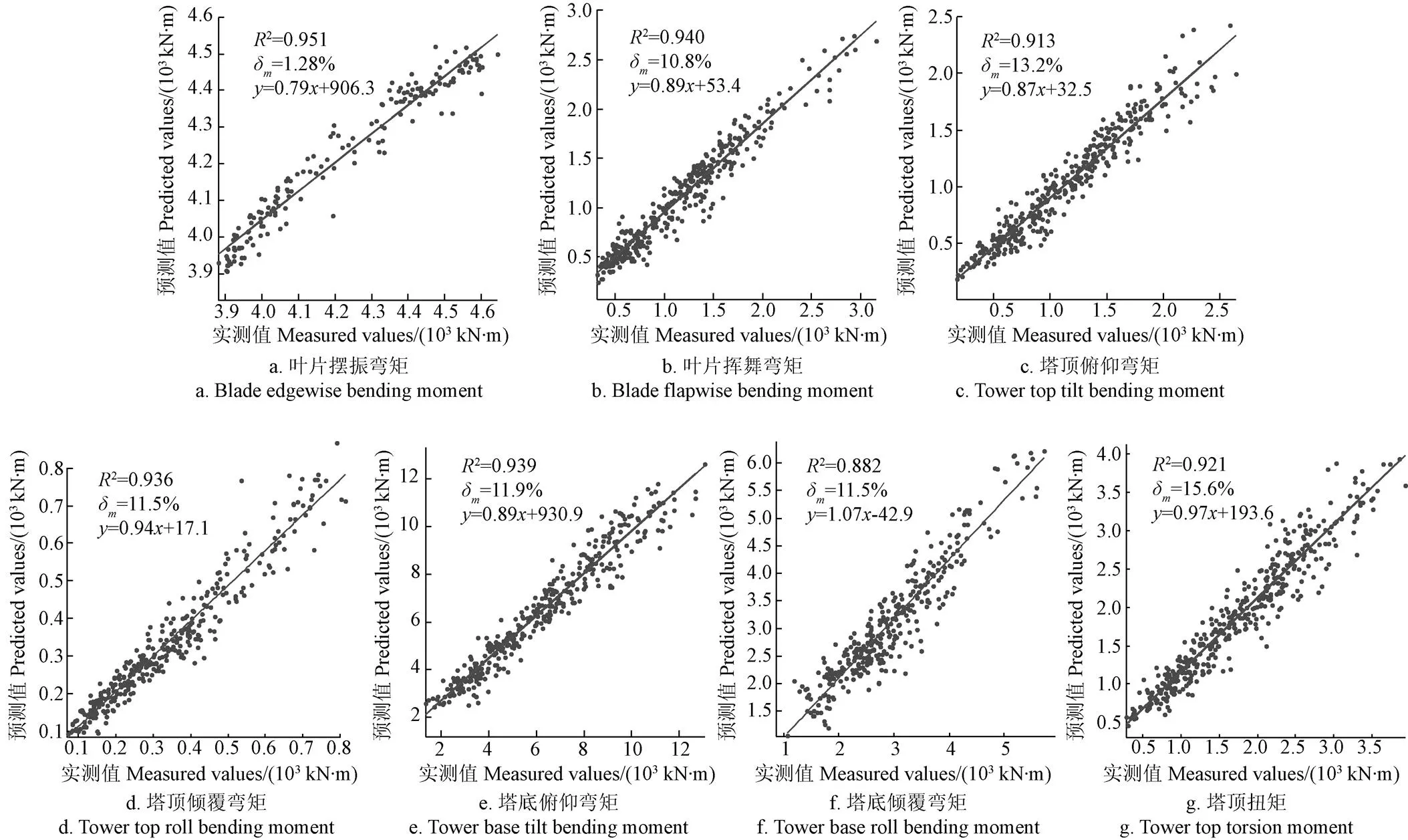
图7 模型预测结果与实测结果比较

由图7可见，由预测值和实测值确定的坐标点大致均匀分布在坐标系第一象限的对角线（45°）两侧，两者的线性拟合如直线所示。图7各子图给出了对应的拟合方程、决定系数2和相对误差的均值δ。其中，叶根摆振和挥舞弯矩的δ分别为1.28%和10.8%，2分别为0.951和0.940，塔筒弯矩的δ在11.5%到15.6%之间，2在0.939到0.882之间，能够满足工程实际需求。行业内机组载荷仿真计算普遍采用商用软件GH bladed进行，文献[29]利用GH bladed软件模拟了9组风况条件下塔底俯仰方向的等效疲劳载荷，9组仿真值与实测值的相对误差均值为9.3%。文献[30]利用GH bladed软件就风电机组极限载荷进行了仿真，仿真值与实测值的对比为：叶根载荷相对误差为12%～19%，塔筒弯矩载荷相对误差为5%～16%。以GH bladed仿真准确度为参照，可见本文模型的预测准确度与主流仿真结果准确度相当。GH bladed软件进行载荷预测需要全面详细的风况信息且计算耗时长，不适用于对风电机组进行实时载荷预测。因此，基于SCADA数据和BP神经网络建立的载荷预测模型能够及时、准确地预测风电机组各关键位置处的等效载荷。

图8是基于SCADA数据，利用BP神经网络对风速进行的预测。所选SCADA数据为轮毂转速的均值和标准差、叶片桨角的均值和标准差、功率的均值和标准差。风速预测结果与实测结果吻合的很好（2=0.984，δ=3.89%）。由此可以认为SCADA数据能够间接表示风速，因此在不使用风速作为模型输入参量时，载荷的预测结果也能达到满意的准确度。

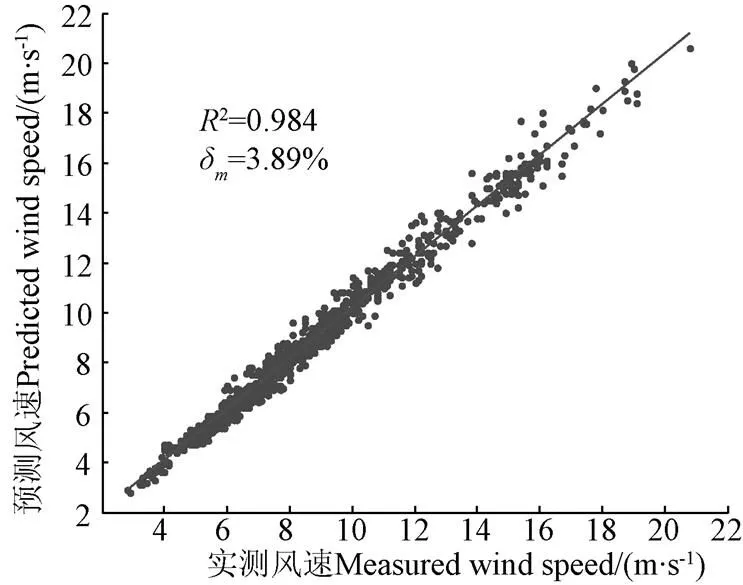
图8 风速预测

4 结 论

以某2.5 MW双馈型风力发电机组为例，本文研究了基于SCADA数据和BP神经网络的风电机组载荷预测方法的有效性。利用BP神经网络建立的预测模型对风电机组7个关键位置处的载荷进行了预测，研究表明：

1）通过处理挖掘SCADA数据，利用BP神经网络建立SCADA数据与载荷间的近似关系，能够对风电机组不同位置、特性不一的载荷进行全面、准确地预测。叶根摆振及挥舞方向弯矩的相对误差分别为1.28%和10.8%，决定系数2分别为0.951和0.940；塔筒各位置的相对误差在11.5%到15.6%之间，决定系数2在0.939到0.882之间。

2）增加与载荷相关的SCADA参量作为模型输入，能够提高预测结果的准确性，以塔底俯仰弯矩为例，增加适当的SCADA参量预测结果的相对误差由12.2%降为11.9%，决定系数2由0.904提高到0.939。因此基于相关性计算的参数选择方法较试错法更适用于参量较多的情况。

3）基于轮毂转速、叶片桨角和有功功率，利用BP神经网络预测的风速与实测风速具有良好的一致性，相对误差为3.89%，决定系数2为0.984，因此在“无风”可用的情况下，利用这3个参量能够弥补风速信息的缺失。

为了实现对整个风电场风电机组载荷的预测评估，进一步的工作应从以下方面开展：1）进一步研究BP神经网络结构与参数对预测模型准确度的影响；2）建立在尾流影响下的风电机组载荷预测模型；3）研究基于单个风电机组建立的关系模型能否推广到其他同类型风电机组的载荷预测中。

[1] 付德义，秦世耀，薛扬，等. 风电机组低电压穿越过程机械载荷特性研究[J]. 太阳能学报，2016，37(5)：1100－1106.

Fu Deyi, Qin Shiyao, Xue Yang, et al. Wind turbine mechanical load characteristics research[J]. Acta Energiae Solaris Sinica, 2016, 37(5): 1100－1106. (in Chinese with English abstract)

[2] 郑小霞，叶聪杰，符杨. 海上风电场运行维护的研究与发展[J]. 电网与清洁能源，2012，28(11)：90－94.

Zheng Xiaoxia, Ye Congjie, Fu Yang. Research and development of operation and maintenance for offshore wind farms[J]. Power System and Clean Energy, 2012, 28(11): 90－94. (in Chinese with English abstract)

[3] 付德义，秦世耀. 基于风力发电机组载荷测试的设计载荷验证[J]. 可再生能源，2013，31(8)：38－44.

Fu Deyi, Qin Shiyao. Wind turbine design load validation based on load measurement[J]. Renewable Energy Resources, 2013, 31(8): 38－44. (in Chinese with English abstract)

[4] 周鹏展，曾竟成，肖加余，等. 基于BLADED 软件的大型风力机叶片气动分析[J]. 中南大学学报：自然科学版，2010，41(5)：2022－2027.

Zhou Zhanpeng, Zeng Jingcheng, Xiao Jiayu, et al. Aerodynamic analysis of a large-scale wind turbine blade based on BLADED software [J]. Journal of Central South University: Science and Technology, 2010, 41(5): 2022－2027. (in Chinese with English abstract)

[5] 庞晓平，梁河，陈进，等. 风力叶片极限载荷评价与分析[J]. 重庆大学学报，2015，38(1)：74－86.

Pang Xiaoping, Liang He, Chen Jin, et al. Evaluation and analysis on the extreme load of wind turbine blade[J]. Journal of Chongqing University, 2015, 38(1): 74－86. (in Chinese with English abstract)

[6] 马林静，刘辉，王树军. 风电机组载荷计算标准的对比研究[J]. 太阳能学报，2015，36(1)：70－78.

Ma Linjing, Liu Hui, Wang Shujun. Comparison research of load calculation standard for wind turbines[J]. Acta Energiae Solaris Sinica, 2015, 36(1): 70－78. (in Chinese with English abstract)

[7] 董礼，廖明夫，Martin K，等. 风力机等效载荷的评估[J]. 太阳能学报，2008，29(12)：1456－1459.

Dong Li, Liao Mingfu, Martin K, et al. Estimation of equivalent load for a horizontal axis wind turbine[J]. Acta Energiae Solaris Sinica, 2008, 29(12): 1456－1459. (in Chinese with English abstract)

[8] Obdam T S, Rademakers L W M M, Braam H. Flight leader concept for wind farm load counting and performance assessment[R]. ECN-M-09-054, 2009.

[9] Obdam T S, Rademakers L W M M, Braam H. Flight leader concept for wind farm load counting: First offshore implementation[R]. ECN-M-09-114, 2009.

[10] Obdam T S, Rademakers L W M M, Braam H. Flight leader concept for wind farm load counting: Offshore evaluation[R]. ECN-M-09-122, 2009.

[11] 戚德虎，康继昌. BP神经网络设计[J]. 计算机工程与设计，1998，19(2)：48－50.

Qi Dehu, Kang Jichang. On design of the BP neural network[J]. Computer Engineering and Design, 1998, 19(2): 48－50. (in Chinese with English abstract)

[12] 高雪鹏，丛爽. BP网络改进算法的性能对比研究[J]. 控制与决策，2001，16(2)：167－171.

Gao Xuepeng, Cong Shuang. Comparative study on fast learning algorithms of BP networks[J]. Control and Decision, 2001, 16(2): 167－171. (in Chinese with English abstract)

[13] 杨刚，陈鸣. 基于BP神经网络的风速预测和风能发电潜力分析[J]. 华东电力，2010，38(2)：304－309.

Yang Gang, Chen Ming. Wind speed forecast and wind power potential analysis based on BP neural networks[J]. East China Electric Power, 2010, 38(2): 304－309. (in Chinese with English abstract)

[14] 裴成玉，张宏明，蒯志要. 基于BP神经网络的载荷试验研究[J]. 港工技术，2014，51(4)：81－83.

Pei Chengyu, Zhang Hongming, Kuai Zhiyao. Load experimental research base on BP neural network[J]. Port Engineering Technology, 2014, 51(4): 81－83. (in Chinese with English abstract)

[15] 童超，郭鹏. 基于特征选择和BP神经网络的风电机组故障分类监测研究[J]. 动力工程学报，2014，34(4)：313－317. Tong Chao, Guo Peng. Wind turbine fault classification based on bp neural network and feature selection algorithm[J]. Journal of Chinese Society of Power Engineering, 2014, 34(4): 313－317. (in Chinese with English abstract)

[16] Le Zheng, Wei Hu, Yong Min. Raw Wind data preprocessing: a data-mining approach[J]. IEEE Transactions on Sustainable Energy, 2015, 6(1): 11－19.

[17] Wind turbines Part1: Design requirements: IEC 61400-1-2005[S].

[18] Wind turbines generator systems-Part 13: Measurement of mechanical loads : IEC 61400-13-2001[S].

[19] 薛扬，付德义，焦渤，等. 一种符合IEC 61400-13 标准的风电机组载荷测试系统: 201010513594 [P]. 2011-02-16.

[20] 付德义，薛扬，秦世耀，等. MW级风力发电机组载荷测试方法研究[J]. 可再生能源，2013，31(3)：65－68.

Fu Deyi, Xue Yang, Qin Shiyao, et al. MW class wind turbine load measurement method research[J]. Renewable Energy Resources, 2013, 31(3): 65－68. (in Chinese with English abstract)

[21] 唐万梅. BP神经网络网络结构优化问题的研究[J].系统工程理论与实践，2005，25(10)：95－100.

Tang Wanmei. The study of the optimal structure of BP neural network[J]. Systems Engineering-Theory & Practice, 2005, 25(10): 95－100. (in Chinese with English abstract)

[22] 田旭光，宋丹，刘宇新. 结合遗传算法优化BP 神经网络的结构和参数[J]. 计算机应用与软件，2004，21(6)：69－71.

Tian Xuguang, Song Dan, Liu Xinyu. Optimizing the structure and parameters of BP neural network based on genetic algorithm[J]. Computer Applications and Software, 2004, 21(6): 69－71. (in Chinese with English abstract)

[23] 高大文，王鹏，蔡臻超. 人工神经网络中隐含层节点与训练次数的优化[J]. 哈尔滨工业大学学报，2003，35(2)：207－209.

Gao Dawen, Wang Peng, Cai Zhenchao. Optimization of hidden nodes and training times in artificial neural network[J]. Journal of Harbin Institute of Technology, 2003, 35(2): 207－209. (in Chinese with English abstract)

[24] 蔡兵. BP神经网络隐层结构的设计方法[J]. 通化师范学院学报，2007，28(2)：18－19.

Cai Bing. Design method on structure of implicit strata in BP neural network[J]. Journal of Tonghua Teachers College, 2007, 28(2): 18－19.(in Chinese with English abstract)

[25] 王德明，王莉，张广明. 基于遗传BP神经网络的短期风速预测模型[J]. 浙江大学学报：工学版，2015，6(1)：837－841.

Wang Deming, Wang Li, Zhang Guangming. Short-term wind speed forecast model for wind farms based on genetic BP neural network[J]. Journal of Zhejiang University: Engineering Science, 2015, 6(1): 837－841. (in Chinese with English abstract)

[26] 沈花玉，王兆霞，高成耀，等. BP神经网络隐含层单元数的确定[J]. 天津理工大学学报，2008，24(5)：13－15.

Shen Huayu, Wang Zhaoxia, Gao Chengyao, et al. Determining the number of BP neural network hidden layer units[J]. Renewable Energy Resources, 2008，24(5)：13－15. (in Chinese with English abstract)

[27] Kung S Y, Hwang J N. An algebraic projection analysis for optimal hidden units size and learning rates in back-propagation learning[J]. IEEE International Conference on Neural Networks, 1988, 1(1): 363－370.

[28] 李洁明，祁新娥. 统计学原理[M]. 上海：复旦大学出版社，2010：314－317.

[29] 付德义，薛扬，焦渤，等. 湍流强度对风电机组疲劳等效载荷的影响[J]. 华北电力大学学报，2015，42(1)：45－50.

Fu Deyi, Xue Yang, Jiao Bo, et al. Effects on the turbulence intensity to wind turbine fatigue equivalent load[J]. Journal of North China Electric Power University, 2015, 42(1): 45－50. (in Chinese with English abstract)

[30] 盛振国，王树军，付德义，等. 风电机组测量载荷工况对比研究[J]. 太阳能学报，2016，37(2)：303－309.

Sheng Zhenguo, Wang Shujun, Fu Deyi, et al. Comparative study on measurement load cases of wind turbine generator systems[J]. Acta Energiae Solaris Sinica, 2016, 37(2): 303－309. (in Chinese with English abstract)

Prediction of wind turbine key load based on SCADA data

Zhou Shidong, Xue Yang, Ma Xiaojing, Wang Wenzhuo

(100192)

The accurate prediction of wind turbine load at crucial positions is of great importance for wind turbines’ structural safety and scheme of operation and maintenance. Traditional load measurements using strain gauges are not suitable for long-term load monitoring because such measurements are labor-intensive, costly and time-consuming. Load simulation using software represented by GH bladed is not applicable to the evaluation of wind turbines’ load because of the failure to get comprehensive information of wind in real time. Therefore, it is necessary to develop an economical and feasible assessment method for wind turbine load. The prediction of wind turbine load may be achieved by establishing the relationship between SCADA data and load measurements. In view of the complicated load condition and coupling relationship among loads, BP (back propagation) neural network is used to construct the relationship between SCADA data and load indicators. The load indicator used in this study is fatigue equivalent load. The SCADA data used as input parameters are selected by calculating the correlation coefficients between SCADA data and load indicators. The numbers of hidden layers and neurons are determined by trial-and-error approach. Taking blade edgewise blending moment as the example, when the rest of parameters of neural network remain fixed, the predicted outputs by the BP neural network with 1 hidden layer and 6 neurons are the most accurate. For other BP neural network models, 1 hidden layer is used and the number of neurons is determined by trial-and-error approach. In order to prove the validity of the model, load measurements at 7 crucial locations of a 2.5 MW wind turbine are carried out. The accuracy of the relationship model is judged by comparing the predicted outputs by the model with the measured values. The coefficient of determination and the arithmetic mean value of relative errors between model outputs and measured values are used to characterize the accuracy. The arithmetic mean values of relative errors are between 1.28% and 15.6%, and the coefficients of determination are between 0.882 and 0.951, which show that the predictions are in good agreement with measurements. Therefore, establishing the approximate relationship between SCADA data and load indicators by BP neural networks can be used as an effective means to achieve the long-term monitoring and evaluation of wind turbine load at crucial locations. In the consideration of the fact that the wind farm seldom has the wind measurement mast and anemometer mounted in nacelle is often affected by the rotating blades, this study has abandoned the wind speed in the load prediction. Using BP neural network, hub rotating speed, pitch angle and active power are used to predict wind speed. The predicted values agree well with the measured value, which indicates that wind speed is not indispensable for the accurate load prediction. The study also shows that better prediction accuracy can be achieved by increasing reasonable input parameters. When there are many SCADA data that can be used as model input, the correlation coefficient approach is more efficient than the trial-and-error approach in selecting model inputs.

wind turbines; models; neural network; SCADA data; parameter selection; fatigue equivalent load; load prediction

10.11975/j.issn.1002-6819.2018.02.030

TK83; TK81

A

1002-6819(2018)-02-0219-07

2017-07-27

2017-12-04

国家电网公司科技项目（NYB17201600300）；国家科技支撑项目（2015BAA07B01）

周士栋，男，主要从事风力发电机组机械载荷、功率特性测试方法与仿真技术研究。Email：zhoushidong@epri.sgcc.com.cn

周士栋，薛扬，马晓晶，王文卓. 基于SCADA数据的风电机组关键载荷预测[J]. 农业工程学报，2018，34(2)：219－225. doi：10.11975/j.issn.1002-6819.2018.02.030 http://www.tcsae.org

Zhou Shidong, Xue Yang, Ma Xiaojing, Wang Wenzhuo. Prediction of wind turbine key load based on SCADA data[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(2): 219－225. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2018.02.030 http://www.tcsae.org