教之以法 授之以渔

江苏省昆山经济技术开发区高级中学 刘胜男

“授人以鱼，不如授之以渔。授人以鱼，只救一时之及；授人以渔，则可解一生之需。”——《老子》

“一个不好的教师奉送真理，一个好的教师则教人发现真理”，这是德国教育家阿道尔夫·第斯多惠的名言。意思是说，在教会学生知识的同时，更应该教会学生学习的方法。这样循序渐进，落实从知识到方法的传授才是教师应该真正做到的。

授之以渔，就要多用启发式教学法。古希腊伟大的哲学家苏格拉底开创的“问答法”，就完美演绎了启发式教学法的过程。在向学生介绍某个概念时，他并不直接告诉学生概念的内容，而是先提出问题，让学生回答。如果学生答错了，他也不直接纠正，而是提出另外的问题，引起学生的思考，从而一步一步、循序渐进地慢慢找到正确的结论。在学习的过程中，学生是学习的主体，要想使学生在基础知识和基本技能的学习中获得更好的效果，就要充分地发挥学生的自主性和主动性。我们在教学上，要多用启发式教学法，不能直接把知识抛给学生去被动接受，而是要启发他们自己发现结论。

比如，在研究切线长的最值问题时，可以先让学生练习定圆外的一个定点所引出的切线长，如，例1：从圆外一点P（2，3）向圆引切线，则切线长为___________。

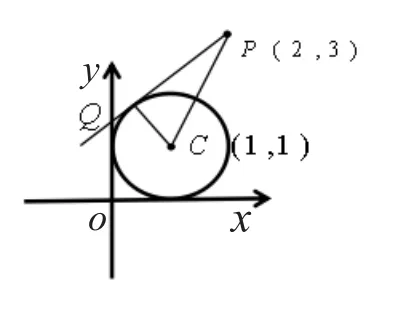
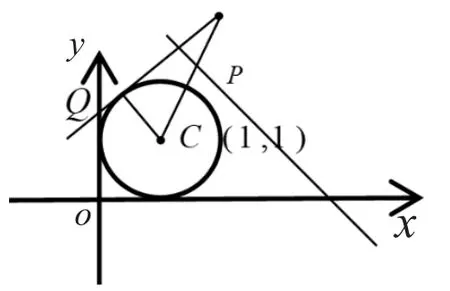
学生都可以顺利解决问题，然后引出变式。

变式1：由直线x+y=5上一点向圆引切线，则切线长最小值为_____。

在学生面对动点问题感到难以解决时，启发学生进行思考，同样是计算切线长，上题我们如何解决的？如何转化切线长？使学生发现，无论动点、定点，一样利用勾股定理，将切线长转化为两点间距离平方与半径平方的差来计算。这样学生得到启发，虽然变式中的切线两端均为动点，但动点之间的距离，可以转化成一个定点（圆心）与一个动点（直线上的点）的距离来解决，从而问题转化为研究一个定点与定直线上的一个动点如何距离最小的问题。到此为止，学生都易于发现问题最终转化为圆心到直线距离的问题。在此基础上，教师还可以再举出其他例子，继续延伸，继续启发学生自己找出解决方案。

通过前面例子，让学生自己尝试，自我启发，在诸多的变化过程中，如动直线l1，是否有什么关系是“定”的？动的垂足P，是否有什么关系是“定”的？在学生实现不了的时候，再给以启发，所谓“不愤不启，不悱不发”，学生自会逐步学会从跟随教师的启发进行思考，到学会在遇到困难时，实现自我启发。多用、善用启发性教学法，从启发学生开始，慢慢让学生习惯于自我启发，才能慢慢达到“授之以渔”的效果。

授之以渔，就要实践因材施教的教育理念。因材施教，就是根据不同的学生，选择不同的材料或者不同难度的例子，让各个层次的学生都容易接受和理解。只有依据学生理解能力的不同，对不同的学生运用不同的例子，才能让他们更易于掌握知识，学会方法，理解精髓。

比如直线过定点的问题，不同学生从不同的题目开始引导。基础较差的同学，可以从下述例子的第（1）小题开始思考；基础好的同学，可以从第（3）小题开始思考；基础非常好的同学可以直接尝试第（4）小题，然后让学生自行总结，定点为何为“定点”？如何才能确定定点？

例3 （1）y=kx+1过哪个定点？

（3）y=kx+3-2k过哪个定点？

（4）若a，b，c成等差数列，则直线y=ax+by+c过哪个定点？

在不同的学习场合，不同类型、不同能力水平的学生，其学习表现也是不尽相同的。需要教师凭着自己的经验、智慧灵活地设计出因材施教的教学实例和教学方法。实践因材施教的教育理念，可以让每位同学都找到自己的参与感，最大限度地让更多学生在课堂中学会处理问题的方法，全面实现“授之以渔”。

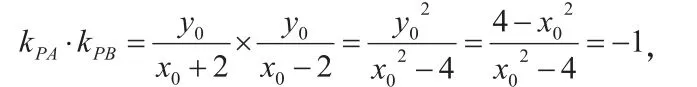
有助于接下来的探究给他们以启发，接下来让他们实践探究：

学生自行经历这些由浅入深，循序渐进的探究过程，慢慢养成自行思考、动手尝试的习惯，从问题的发现，到思考、探究，进而自行解决问题，这是实现“授之以渔”的必经之路。陶行知先生说过：“教学做是一件事，不是三件事。我们要在做上教，在做上学。不在做上用功夫，教故不成为教，学也不成为学。”在平时的教育教学过程中，我们要践行“教学做合一”，坚持给予学生付诸实践的机会，养成探究的习惯，才能真正实现“授之以渔”。

第斯多惠还曾说过，任何真正的教学不仅是提供知识，而且是给予学生以教育。作为一名优秀的数学教师，仅仅“授人以鱼”是不够的，而当我们深刻理解到“授人以渔”的本质，才能教出更好的学生。从端正学生态度、善用启发式教学法、实践因材施教的教育理念、养成探究的习惯三个维度去落实“授之以渔”，只有这样，才能真正地落实素质教育，而我们的教育改革才能走得更远。