圆的直径式方程的一个应用

北京丰台二中

甘志国 (邮编：100071)

普通高中课程标准实验教科书《数学2·必修·A版》(人民教育出版社，2007年第3版)第124页第5题的结论也可叫做圆的直径式方程：

设A(x1,y1),B(x2,y2)，则以线段AB为直径的圆的方程是

(x-x1)(x-x2)+(y-y1)(y-y2)=0

①

证明可设u(x)=t(x-x1)(x-x2),v(y)=t(y-y1)(y-y2)(t≠0)，所以由圆的直径式方程得以线段P1P2为直径的圆的方程是①，也即u(x)+v(y)=0.

推论1设直线l:x=h与二次曲线Γ:f(x,y)=0(这里式子f(x,y)中y2的系数是1)交于不同的两点Pi(h,yi)(i=1,2)，则以线段P1P2为直径的圆的方程是(x-h)2+f(h,y)=0.

推论2设直线l:y=t与二次曲线Γ:f(x,y)=0(这里式子f(x,y)中x2的系数是1)交于不同的两点Pi(xi,t)(i=1,2)，则以线段P1P2为直径的圆的方程是f(x,t)+(y-t)2=0.

例1已知直线l:y=x+3与抛物线C:y=x2交于不同的两点Pi(xi,yi)(i=1,2)，求以线段P1P2为直径的圆的方程.

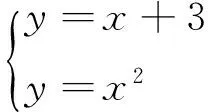
x2-x-3=0,y2-7y+9=0

由定理可得所求答案为(x2-x-3)+(y2-7y+9)=0，即x2+y2-x-7y+6=0.

(1)求直线AB的斜率；

(2)设M为曲线C上一点，C在M处的切线与直线AB平行，且AM⊥BM，求直线AB的方程.

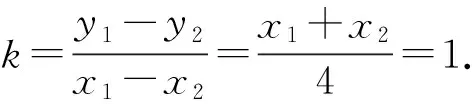
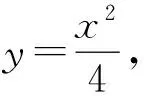
可设直线AB:y=x+m.

x2-4x-4m=0,y2-(2m+4)y+m2=0

由题意知Δ>0，得m>-1.

由定理可得以线段AB为直径的圆的方程是(x2-4x-4m)+[y2-(2m+4)y+m2]=0.

再由AM⊥BM，可得M(2，1)在这个圆上，进而可求得m=7(舍去m=-1)，因而所求直线AB的方程是y=x+7.

例3(2017年高考全国卷III理科第20题)已知抛物线C：y2=2x，过点(2，0)的直线l交C与A，B两点，圆M是以线段AB为直径的圆．

(1)证明：坐标原点O在圆M上；

(2)设圆M过点P(4，-2)，求直线l与圆M的方程．

解(1)显然，当直线斜率为0时，直线与抛物线交于一点，不符合题意．因而可设直线l:x=my+2.

x2-(2m2+4)x+4=0,y2-2my-4=0

可得Δ>0恒成立，所以直线l与抛物线C总有两个不同的交点.

由定理可得以线段AB为直径的圆M的方程是[x2-(2m2+4)x+4]+(y2-2my-4)=0.

进而可得坐标原点O在圆M上.

(注：此问的一般情形是以下经典结论：若直线l与抛物线y2=2px交于两点A,B,O是坐标原点，则OA⊥OB⟺直线l过点(2p,0).)

当m=1时，可得直线l的方程是x-y-2=0，圆M的方程是 (x-3)2+(y-1)2=10．