简化运算 助力高考

江苏省如皋中学高一(1) 班

孙心怡 (邮编：638400)

江苏高考对数学能力的考查主要包括空间想象、抽象概括、推理论证、运算求解、数据处理这几方面的能力.其中运算能力的考查要求是：能够根据法则、公式进行正确运算、变形和数据处理；能够根据问题的条件寻找与设计合理、简捷的运算途径；能够根据要求对数据进行估计或近似计算.

一道直线与椭圆的试题，老师给出了参考答案供我们学习，布置各小组从参考答案出发研究计算的方法.有没有其他简单的运算途径？如何简化？激发了我们小组思考、探究的热情.多角度思考，层层深入，钻研的过程，让我们经历了一次又一次思维的洗礼.巩固了知识，熟悉了方法，有烦恼更有收获.对江苏高考运算能力的考查要求有了切身的体会与理解.回味过程，其乐无穷，特此飨志趣相投者.

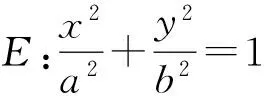
(1)求椭圆E的标准方程；

(2)若△ABC是以点C为直角顶点的等腰直角三角形，求直线l的方程.

1 学习总结 把握本质 力求变化

通览参考答案，其实第(2)小题就是解方程组

①

②

采用代入消元的方法，由于①式是关于y0的二次方程，②式是关于y0的一次方程，所以参考答案从②式中解出y0，再代入①式.

上述两个方程均比较复杂，因此在运算时要注意观察式子的特点，寻找合理的运算方向，切不可乱化，从而掩盖式子的特征.

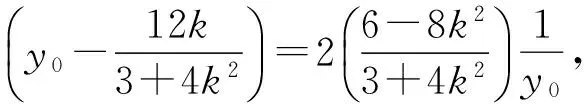
2 不同路径 出现增解 等价相助

通过对解题过程的反复确认，上述解题过程无误，为什么会出现增解？如何取舍？为什么代入方程①就不会出现，代入方程②就出现麻烦，两者的区别究竟在哪里？

小组成员一时陷入了沉思，或重新运算，或回忆做过的一些试题，或查找资料，都想首先发现问题的症结，大家都在挖空脑力地思考.

回忆慢慢袭来，老师曾经说过，如果在推导的过程中出现了不等价的现象，就会出现增解，而这样的问题从前向后去查找根本找不出，应该从后向前来思考.一石激起千层浪，大家茅塞顿开，兴奋得手舞足蹈.

要满足题意，必须同时满足

①

②

而代入①式就是解方程组

只要将第二个方程代入第一个方程就可以推导到前面的两个方程，因此这两个方程组之间是等价的.不会出现增解.

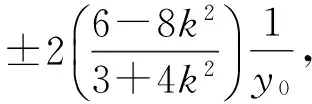
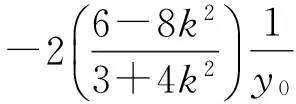
3 反思过程 寻求突破 简化运算

上述运算较为繁琐，方程组也较为复杂，有没有更简捷的运算途径.条件还有其他的使用方法吗？点B的坐标能求，一定要求吗？带着这些疑问小组内进行了分工突破，再合作交流，分享智慧的成果.

突破一等腰直角三角形这个条件可不可以通过变形使用或等价使用，达到计算思路更明确，最终简化运算的目的.

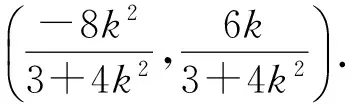
当k=0时，此时B(2,0)，AB的中垂线为y轴，在y轴上一定存在点C，使得△ABC是以点C为直角顶点的等腰直角三角形.

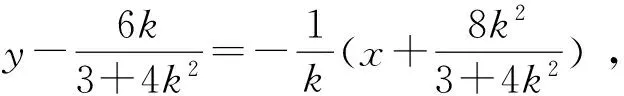
上述等价使用等腰三角形这一条件，使得运算的方向非常明确，运算程序可操作，组内成员都能够快速算出，非常贴近我们学生的实际.

突破二等腰三角形ABC中AC=BC，除了等价使用可以简化外，在长度计算上是否也可以有简化的方法？经过讨论研究发现长度除了使用两点之间的距离外，还可使用弦长公式.

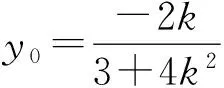
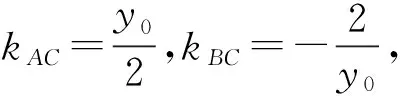
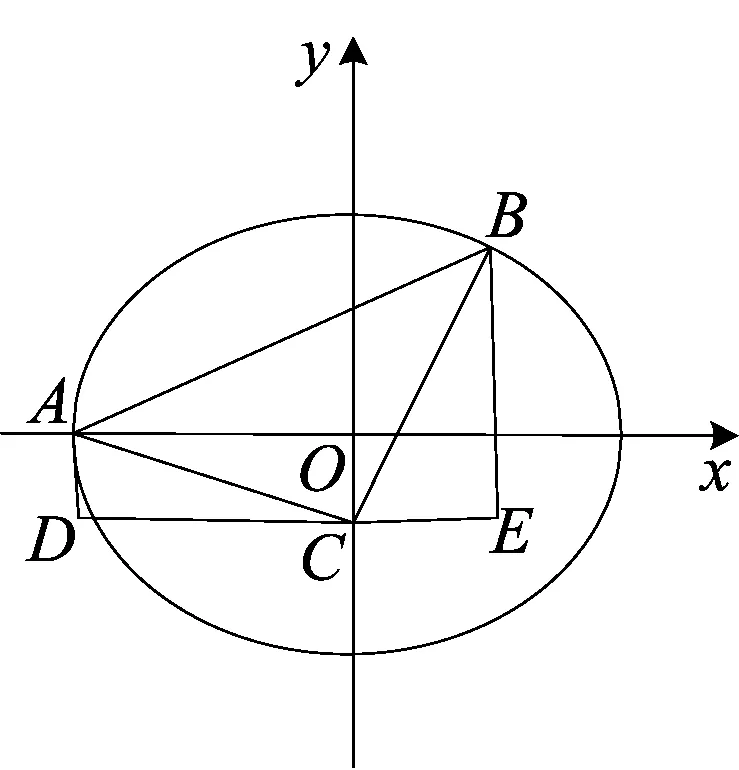
突破三等腰直角三角形有很强的平面几何性质，能否通过平面几何的方法实现对解析几何运算的简化？

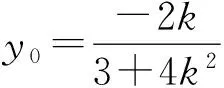
突破四参考答案的运算过程给人的感觉很烦，其原因在于B点的坐标虽然能求，但比较复杂，是否可以不求而设出来，通过其满足的等量关系来限制呢？我们进行了尝试，成功了.

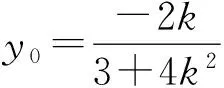
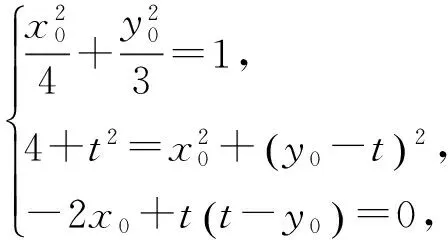
代入椭圆方程可得

小组讨论中大家既有分工又有合作，分工是速度与准确率的比拼，合作则是数学思维的碰撞，全情的投入让小组讨论更高效，每一个一闪而过的念头都不会放过，要么尝试、要么否定，都需要给出充分的能让组员认可的理由.细细品味讨论的过程，它让所学知识灵动起来、灵活起来、交汇起来，其中有困惑，有惊喜，更有满满的收获，让我们对下一次的讨论研究充满期待.