“数独游戏”算法探析

夏一涵

本文介绍数独游戏的一种算法.该算法中多次使用回溯法，初始化时，先随机生成符合规则的终盘，然后在此盘中挖空，每次挖空后保证数独有唯一解，解不唯一时进行回溯，空格数等于游戏难度规定的数量时停止挖空，形成数独初盘，供游戏者填写.

一、概论

数独（Sudoku）是一种运用纸、笔进行演算的逻辑游戏，有四阶数独、六阶数独和九宫数独.例如图1就是一个九宫数独题，每一行称为数独的行，每一列称为数独的列，每一个小九宫格称为数独的宫.数独的基本规则就是每一行、每一列、每一宫中，1～9这9个数字都只出现一次.

玩家需要根据9×9盘面上的已知数字，通过推理填写出所有剩余空格的数字，并满足每一行、每一列、每一个粗线宫内的数字均含1～9，不重复.

设计一个数独游戏系统，包括以下功能：

（1）难度调节，包括简单、中等、困难模式；

（2）游戏功能；

（3）游戏计时功能，记录当局游戏所需的时间；

（4）游戏成绩统计功能，每局游戏结束后自动统计游戏时间作为成绩，并在排行榜里显示最快的10名；

（5）规则说明等.

图1 数独游戏演示

二、需求分析

1.功能性需求

数独游戏需要生成符合数独要求的题目.首先，从数独题目的正确性考虑，需要一个Sudoku类，其中的create（）方法能生成一个满足数独要求的9×9的数组，这个数组就是数独的终盘，也是最后生成的数独初盘的唯一解；其次，为了验证数独初盘是否只有唯一解，需要一个Solution类，该类的初始化需要输入一个数独初盘，然后通过该类的cal（）方法计算该数独的解的数量，并返回解的数量；此外还需要一个模块Problem类，其中的create（）方法能根据游戏难度在该数组中随机挖掉一定数量的数，在此期间要保证数独的解仍然唯一，然后返回已挖去一些值的数组和原数组，作为数独的初盘和终盘.挖掉一些数之后的数组经过简单的格式整理之后就是一道数独的题目了.

界面部分，需要9×9个输入框，用于显示题目中的数字，并让玩家完成剩下的数字.1个数字框，用来显示游戏时间；一个排行榜，用来显示各个难度的最快通关时间；六个按钮，其中三个用于调节难度，其他三个分别用于“显示答案”、“再来一局”和“退出”的功能.此外，可以在帮助菜单里获得游戏的规则说明.

2.非功能性需求

游戏设计需要注重玩家的游戏体验，只有最基本的功能是不够的.显示界面需要更加人性化.为了便于玩家区分题目中已有的数和自己填的数，需要用不同的颜色区分.数独中，每个3×3的小格也需要包含1～9，不重复，为了便于玩家观察，也为了游戏界面更加美观，每个相邻的3×3的小格需要用不同的背景色加以区分.

算法方面，生成一个满足要求的题目并不是一件容易的事.为了保证游戏程序的流畅运行，所有生成题目的算法都需要执行得足够快，从而避免让玩家感觉到卡顿.虽然可以通过提前生成题目库的方法减少运算时间，但这会导致游戏文件过大，且题目有限，无法生成足够多的游戏局面.

3.需求建模

游戏后端算法由3个模块组成.

（1）Sudoku类用于生成一个如图2的符合数独要求的终盘，这个终盘将被用于生成数独初盘：

（2）Solution类用于计算一个数独初盘的解的数量.

（3）Problem类调用Sudoku类和Solution类生成一个数独初盘，并确保这个初盘有且仅有一解.

图2 终盘

三、概要设计

1.Sudoku类设计说明

图3是该模块的Sudoku类生成数独终盘的流程图.

如图3所示，该类使用了回溯法，最终生成一个完整的满足约束条件的数独终盘.

回溯法（探索与回溯法）是一种选优搜索法，又称为试探法，按选优条件向前搜索，以达到目标.但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种“走不通就退回再走”的算法称为回溯法，而满足回溯条件的某个状态的点称为“回溯点”.

该类先生成9×9个空格.依次往空格中填数，填入的数要满足每一行、每一列、每一宫都不能有重复的数，并在满足这3个要求的可选的几个数中随机选择一个填入.为找到满足这个要求的数，需要建立3个集合.集合1是数独中所有可填的数，即｛1，2，3，4，5，6，7，8，9｝；集合2是通过遍历需要填写的空所在行、列和宫中的所有数生成的集合.集合2中的数不能填写在目标的单元格中.集合3通过求集合1与集合2之差得到.集合3中的数就是目标单元格的可选的值.如果某一单元格中没有任何满足条件的数，即集合3为空集，则说明上一个数填错了.在上一层可选的几个数中排除当前填写的数，再次随机选择一个数填入，并继续填入之后的空格.如果上一层也没有任何满足条件的数，则再往上一格回溯……以此类推，直至填完所有空格.

回溯法与穷举法有某些联系，它们都是基于试探的.但穷举法要将一个解的各个部分全部生成后，才检查是否满足条件；若不满足，则直接放弃该完整解，然后尝试另一个可能的完整解，它并没有沿着一个可能的完整解的各个部分逐步回退生成解的过程.而对于回溯法，一个解的各个部分是逐步生成的，当发现当前生成的某部分不满足约束条件时，就放弃该步所做的工作，退到上一步重新进行尝试，而不是放弃整个解重来.使用回溯法生成数独初盘看似暴力，但随着填入的格子的数量的增长，未填的格子的选择会迅速减少.经10000次测试，完成一个9×9的数独初盘，平均只需要填入132次，即回溯51次就可以完成.有兴趣与耐心的话，完全可以用纸、铅笔、橡皮按程序的方法手动生成一个数独终盘，平均下来只需要擦51个空，就可以填完.

图3 生成数独终盘的流程图

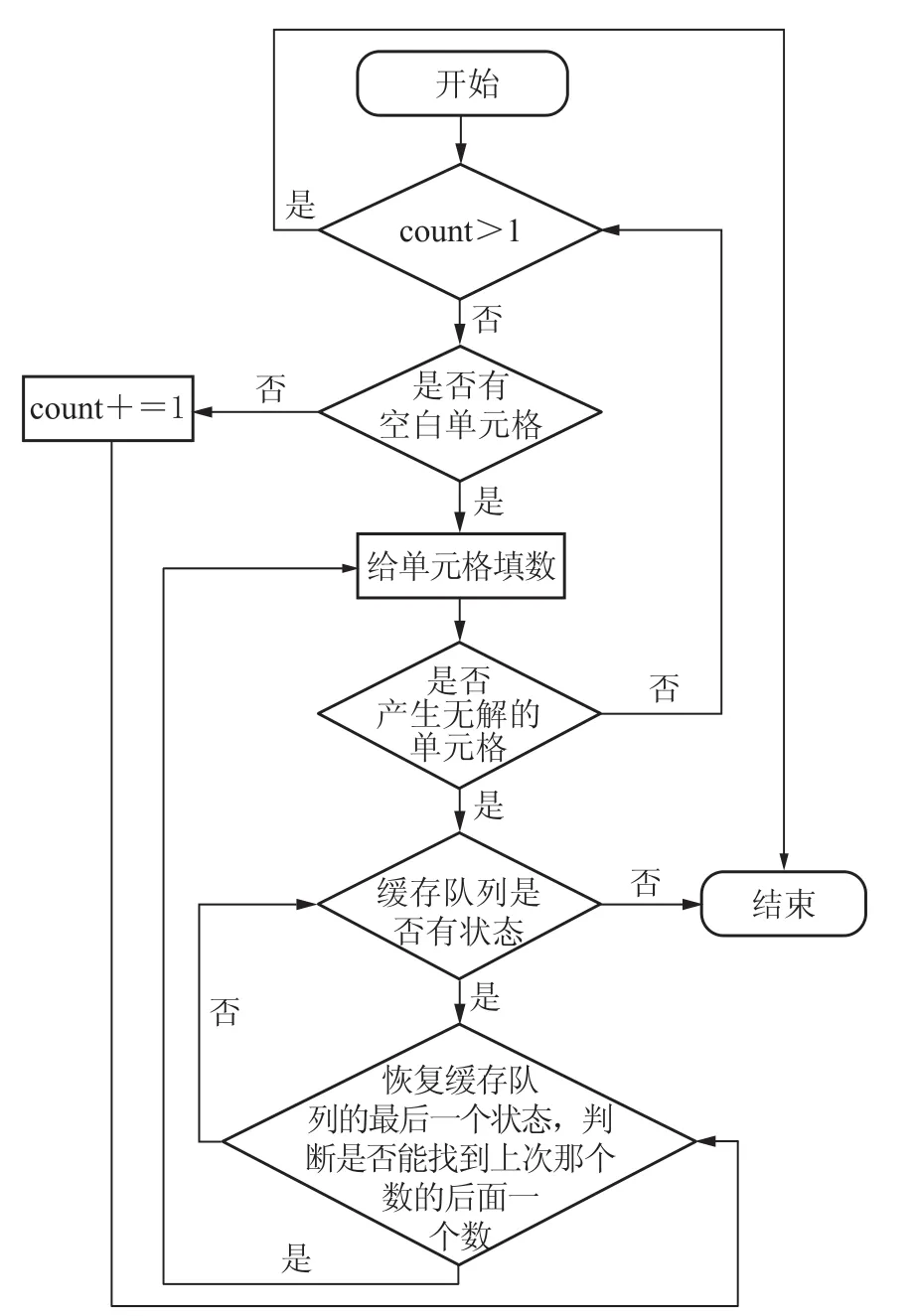
图4 计算数独解的个数流程图

2.Solution类设计说明

Solution类用于计算数独解的个数.图4是Solution类用于计算数独解的个数的流程图.

如图4所示，该算法也使用了回溯法，最终可以计算出一个数独到底是无解、有唯一解还是有多解.

该算法使用回溯法计算数独的解的个数.在空格中按从小到大的顺序依次尝试该空格的可行解，并递归地填写下一个空格.如果某一空格遇到无法填入或所有解都已经尝试过的情况，就回溯至上一层，上一层接着填写下一个可行解；如果填入的是最后一个空格，就给计数器加1，再回溯至上一层.当计数器中的值等于2时，已经可以确定该数独的解一定不唯一，不必继续运算浪费时间，直接退出运行；如果数独的解的数量小于或等于1，程序会在遍历所有情况后结束，并在计数器里记录下解的数量.

3.Problem类设计说明

该类同样通过回溯法产生有唯一解的数独初盘.它先通过Sudoku类生成一个数独终盘，复制生成的初盘并在复制的初盘上不断挖空，每挖空一次，就调用Solution类计算数独解的数量，看数独的解是否仍然唯一.如果某次挖空导致数独产生了多解，将该空填回去，并改挖其他空；如果某一状态下，无论挖掉哪一格，都会造成数独产生多解，则需回溯至上一层，即补回上一次挖掉的空.当挖掉的空的数量达到预设的值时，停止挖空.此时被挖空的数独就是数独的初盘，也是数独游戏的题目.挖空之前的数独初盘，就是题目的答案.

四、程序截图

图5 集成测试结果

图6 显示答案测试结果