利用次数关系简化不等式问题

张 鹏

在高中数学涉及的基本不等式a＋b≥中，观察发现，这是一个不等式前后次数不变的不等式.若我们更强调其中的次数关系及一般性，可把此式推广为

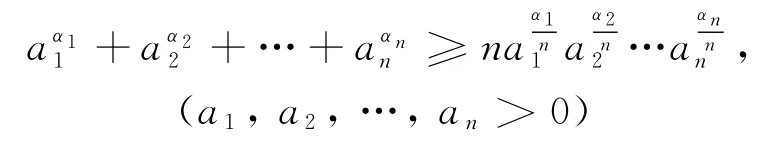
即把一个多项式与一个单项式做大小比较，且该单项式的次数为多项式各项次数和的算术平均数.利用这个关系，我们可以对较为复杂、含有较高次数多项式的不等式问题进行简化.

例1已知a＞0，b＞0，ab＝1，求证：

分析1要将左式中的一次项转化为右式中的次项，添加零次项来使用均值不等式进行降次是常用手段，易知

分析2注意到的次数关系，将a＋b化成与有关的式子.

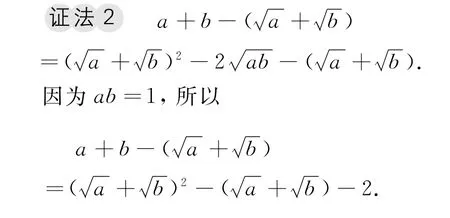
变式 已知a＞0，b＞0，c＞0，abc＝1，求证：

证明

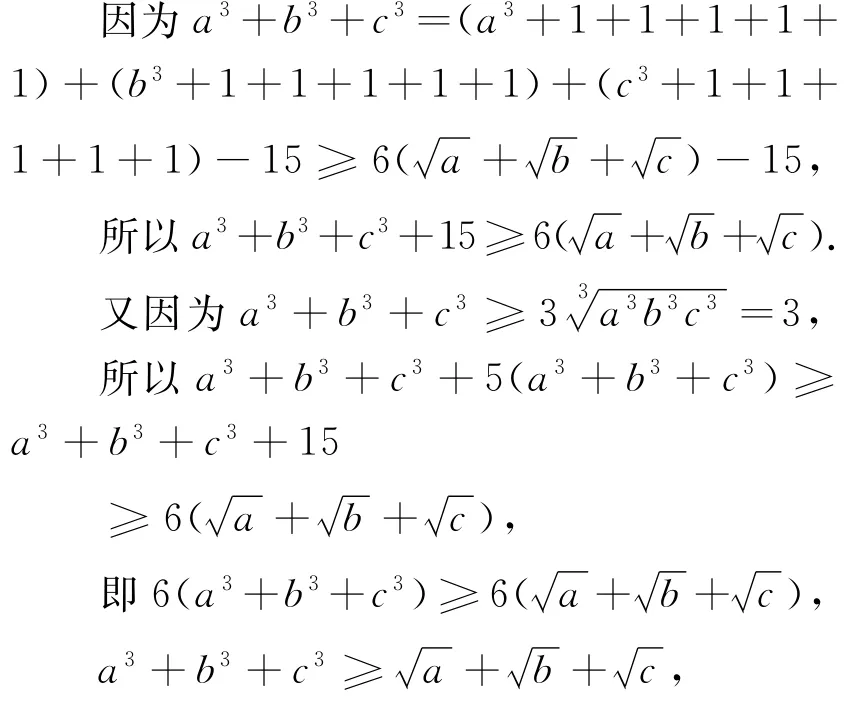
当且仅当a＝b＝c＝1时取等号

例2a，b＞0，ab＝1，则的最小值是________.

分析目标式的分母中出现平方项，次数较高，可考虑利用均值不等式把分母调整为一次式.观察发现，a＝b＝1时，可猜测此时取到最小值并证明.

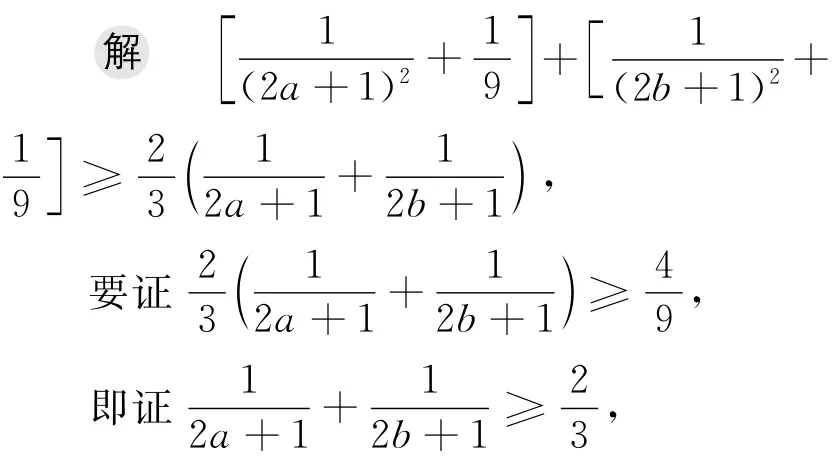
通分化简得：

所以命题得证，当且仅当a＝b＝1时取等号，此时

例3若正数x，y满足15x-y＝22，则x3＋y3-x2-y2的最小值为________.

分析本题最常见的解法是代入消元，然后用导数解决，我们先来看一下使用这种解法的解题过程：

则f′（x）＝8（633x-935）（2x-3），

所以f（x）在单调递增，在单调递减，在单调递增.

然而这样的解法计算太过繁杂.若从另外一个角度分析，由15x-y＝22，可以发现x＞1，将x3＋y3-x2-y2写成x2（x-1）＋y2（y-1），若y＞1，则x3＋y3-x2-y2不可能有最小值，因此0＜y＜1，从二分法的角度思考，猜想再用基本不等式证明.要把x3＋y3-x2-y2调整为含15xy的形式，需要利用均值不等式进行降次.

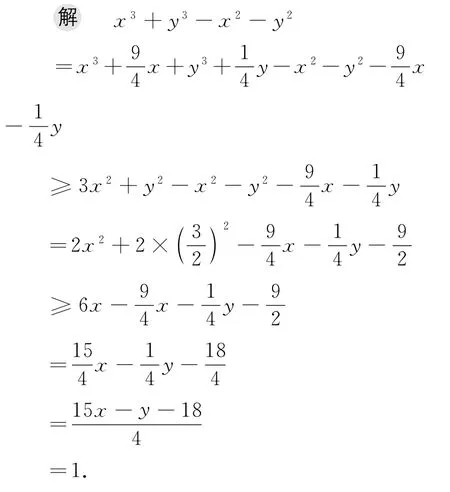
这种解法的运算难度远小于上一种，虽看似难以想到，但若能透彻理解不等式前后次数变化的关系，稍加猜测，就很自然了.

通过攻克以上题目，我意识到平时对基本公式、基本定理等一定要烂熟于心，吃透理解.由这些公式或定理推广的一般结论往往能为我们的解题提供助力，使我们胸有成竹，从容应对考试.