思路贯通，茅塞顿开

沙国祥

思路思路，学生解题，最恼的是没有思路.

既是路，则需贯通.知识之间，问题之间，如若孤岛相隔，即使你掌握的知识、会解的题目很多，也常思路阻塞，甚至无从下手.如同貌似强大的敌军，一旦各路兵马互不接应：或失去联络，或被我神兵插入，陷入各自为战、首尾不顾状态，离失败就不远了.

解题，无非是打通条件和结论，在知识之间铺就联系的通道.比如勾股定理，就是在条件“已知三角形是直角三角形”和结论“斜边的平方等于两条直角边的平方和”之间，铺路架桥.不过，条件和结论乍看似乎风马牛不相及，寻得思路并非易事.由于边的平方即意味着以此边为边长的正方形的面积，故证明勾股定理的思路大多是面积法.有此想法，利用直角三角形的特征，则任你切割拼补，十八般武艺，三百多种证法，大抵离不开“面积不变”这条路、这个魂.

学习圆锥曲线，同样要拽住知识之间的连线，才能贯通解题思路.

如何将思路贯通？常见的是纵横联系.纵，为时间轴，与已学的知识接上头；横，为空间轴，将割裂的知识点、知识块连上线，如此打破时空隔阂，路路连通，纵横交错，思路自然就有了.

比如，学习椭圆，就可以和以前学过的圆相联系.如，椭圆看起来是“扁的”，是否可以由圆在一个方向上均匀压缩而得呢？

半径为a，圆心在原点的圆的方程是x2＋y2＝a2，沿y轴方向纵向压缩（即横坐标保持不变，纵坐标变为原来的倍），设得到的新曲线上任意一点的坐标为（x′，y′），则有代入圆的方程x2＋y2＝a2，得

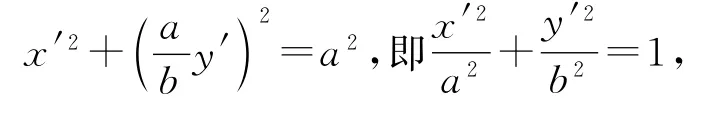
这就是椭圆的标准方程.

这样一来，求长半轴长为a，短半轴长为b的椭圆的面积，也可以视为由圆的面积缩小而得如果用微积分求椭圆的面积，还得费不少周折呢！

再如，我们知道中心在原点、焦点在x轴上的双曲线标准方程为但初中学到的双曲线，则是指函数的图象，化成xy＝k的形式，也和相去甚远.其实，这是由于坐标系选择的不同，导致方程的形式迥然不同.

我们来比较一下，双曲线xy＝k有这样的特性：双曲线上任意一点（x，y）到x轴、y轴（双曲线的渐近线）的距离之积为定值；反过来，双曲线xy＝k也可以看成到x轴、y轴的距离之积为定值、且位于第一、三（或二、四）象限的动点的轨迹.那么，双曲线是否也可以视为到直线（双曲线渐近线方程）的距离之积等于定值k（且与x轴相交）的点的轨迹呢？

设（x，y）是满足条件的动点，则有只要取0，即得

说了椭圆、双曲线，我们也别忘了抛物线哦！

初中我们就学过抛物线了，与它相应的二次函数y＝ax2＋bx＋c（a≠0），可以看做一个二次方程，但，这可不是一个标准的抛物线方程！通过配方：我们可以知道它的顶点位于令得方程y′＝ax′2，即可化为现在所学的标准方程（相当于坐标系的原点移到抛物线的顶点处）.这样联系起来，初中、高中的抛物线就是一回事.

有一道关于抛物线的习题：

过抛物线的焦点作一条直线，与抛物线交于两点A，B，分别过A，B引抛物线准线的垂线，垂足依次为C，D，求证：A，O，D在一条直线上，B，O，C也在一条直线上.

这道题，用解析法可以这样证：

设抛物线的标准方程为y2＝2px，计算AO和DO的斜率，再利用焦点弦端点坐标的性质y1y2＝-p2，思路打通.

但这样计算得到的结论，总给人一种“巧合”的感觉.

有兴趣的同学不妨深入探讨本题与下面这道几何题之间的联系：

如图，AC∥BD，AD与BC交于点O，AF＝AC，BF＝BD，点E在DC上，且EF∥BD.求证：（1）E，O，F三点在一条直线上；（2）OE＝OF.

图1

（提示：（1）由AC∥BD得又AF＝AC，BF＝BD，故所以OF∥BD；（2）证

因此，学习圆锥曲线，我们可以将其与已经学过的或其他数学分支的知识（函数、平面几何等）联系贯通，甚至可以与其他学科的知识牵起手来.如，圆锥曲线具有极佳的光学、声学性质，用解析几何甚至平面几何的知识，均可以证明这些性质.

如此，知识相连，思路贯通，你成为解题高手，便不再是梦想.