倾听数学与音乐的神奇交响
2018-02-26张志勇
张志勇
《梁祝》优美动听的旋律,《十面埋伏》的铮铮琵琶声,贝多芬令人激动的交响曲,田野里昆虫啁啾的鸣叫……当你沉浸在这些美妙的音乐声中时,是否曾想过它们其实与数学有着密切的联系?
“多情外化”的音乐与“严谨抽象”的数学间确实存在剪不断、理还乱的缘分.姑且不提音高的数学本质,也不论曲式结构中的数学规律,只从乐曲中最基本的简谱音符“1,2,3,4,5,6,7”是人们应用或提及最为频繁的数字便可见一斑.事实上,乐音之所以和谐、悦耳、动听,是因为它有着周期性的振动频率(如国际标准音a1的振动频率是每秒钟440次,e2是每秒钟660次,a2是每秒钟880次);一组和声(不同音高的乐音的组合)之所以能给听众以悦耳的体验,是因为组成这组和声的音频间有协和的比例关系(能表示为简单整数比).德国著名数学家莱布尼兹说:“音乐,就它的基础来说,是数学的;就它的出现来说,是直觉的.”而爱因斯坦说得更为风趣:“我们这个世界可以由音乐的音符组成,也可以由数学公式组成.”
物理学知识告诉我们,声音是由振动产生的,乐音也不例外,而三角函数正是对振动波的数学描述.这样,音乐与数学之间的不可思议的天然联系,恰可以用三角函数知识来加以阐释.
我们知道,乐音有响度、音调、音色之分.如果用正弦函数y=Asin(ω t+φ)来表示声音的话,那么响度反映声音的强弱,由振动的振幅A决定,振幅越大声音越强响度也就越大;音调反映声音的高低,由振动的频率决定,频率越高振动越快音调也就越高;音色是什么呢?简单地说,笛子和小提琴发出的声音、男生和女生的声音,即使响度相同、音调相同听起来也有明显的差别,这就是音色.
乐音一般都不是单一的,而是由许多不同频率的声波合成的周期函数,法国数学家傅里叶告诉我们,“一个周期函数可以表示成正弦函数之和.”因此,任何乐音都可以表示为简单的正弦函数之和,都是形如“Asin(ω t+φ)”的各项之和,其中每一项都代表一种有适当频率和振幅的简单声音.这些声波中有一个频率最低、振幅最大的声波,通常称之为基音(可以用y=A1sin(ω t+φ1)来表示);乐音中除了基音之外还有许多其他频率的声波,称为泛音,泛音的频率分别是基音频率f的整倍数2f,3f,…,振幅随着频率的升高而降低,分别为A2,A3,…,这样泛音可以分别用y=A2sin(2ω t+φ2),y=A3sin(3ω t+φ3),…,y=Aksin(k ω t+φk),…来表示,基音和所有的泛音合在一起,就是以上那些正弦函数的和y=A1sin(ω t+φ1)+A2sin(2ω t+φ2)+…+Aksin(k ω t+φk)+….由于各个正弦函数系数比例不同,也就是各个泛音与基音的强弱的比例不同,就产生了不同的音色.
为了体会按不同的响度比例将基音和泛音合成起来会产生什么效果,我们来观察不同的频率的正弦函数按不同比例叠加起来得到的函数图象.
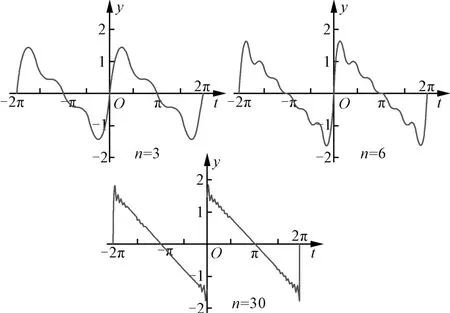
图1
观察图象可以发现,n=3与n=6,n=30时一样,函数的周期均为2π;也就是说,y= sinx的周期是的周期是π,将它们加起来得到的函数也有周期甚至都有周期2π.
进一步地,随着n的增加,以2π为周期的函数图象越来越接近于“锯齿形”的波,这个“锯齿形”的波正是由各种频率的正弦波 sinkx分别乘以系数之后叠加起来的(如图2).
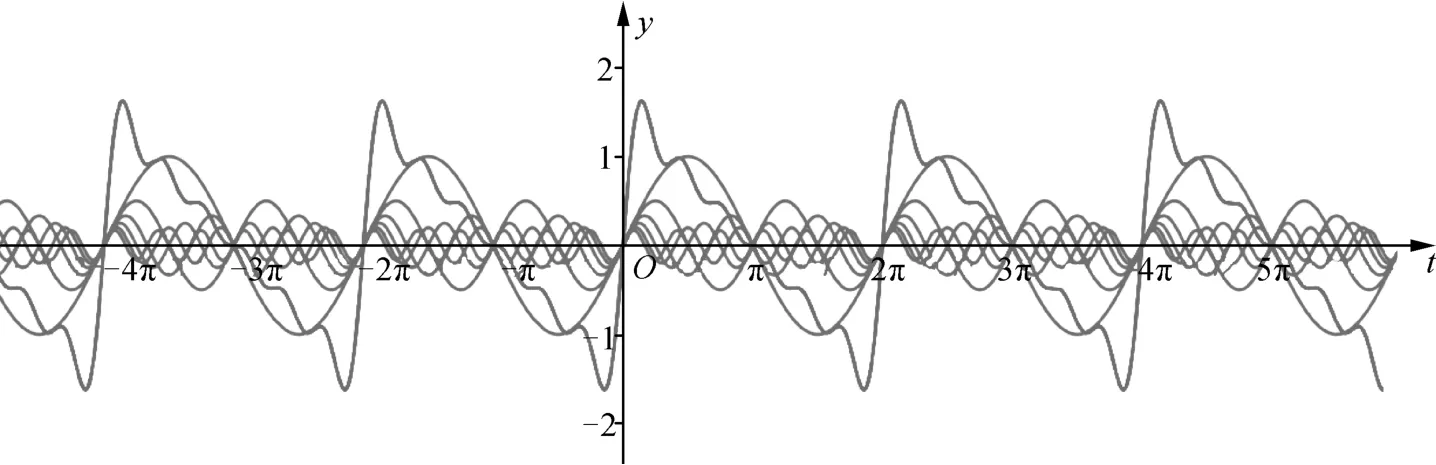
图2
多么令人惊讶呀!有了三角函数,世界上的声音一下子变得简单了,不管是雷鸣、鸟啼、人语或是钢琴的鸣奏,都可以归结为简单声音的组合,这些简单声音用数学表示就是三角函数.电子琴正是通过调整各个泛音响度的比例,来模拟各种不同乐器(如钢琴、小提琴、大提琴、长笛等)发出的声音.
我们前面的讨论只是纸上谈兵,有兴趣的同学可以下载一些手机APP软件来模拟做一个音乐制作人,具体操作办法如图3所示,在应用宝中以“音乐模拟”为关键词搜索,会跳出很多应用软件(如图3-1);以“模拟钢琴”为例,下载安装打开后,软件界面如图3-2所示,按键下去就可以发出相应的乐音,点击图3-3所示的设置按键,还可以将你的独创音乐录下来进行发布.
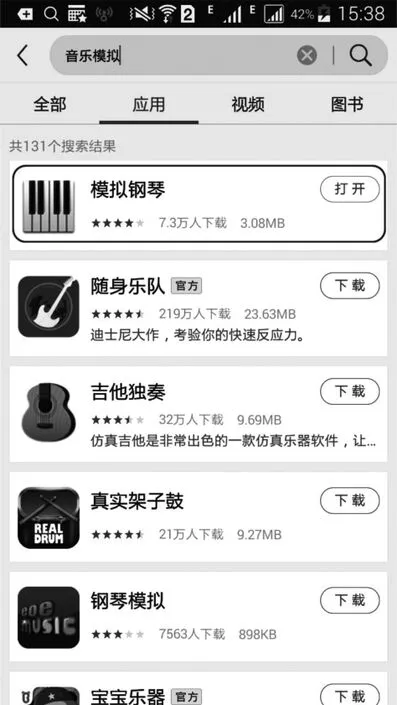
图3-1
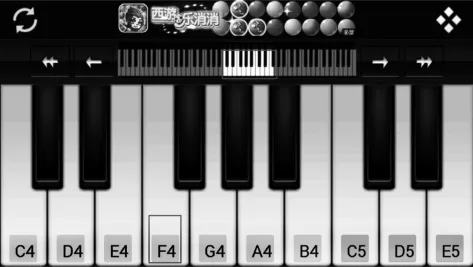
图3-2

图3-3
世界上的声音是如此丰富,却又如此简单.看似感性、灵动的音乐,实际上依赖于严谨的数学规律作为其运作的基础.数学因抽象而美,音乐因艺术而美,这两者的相互渗透和关联,必然会使得这两种美交相辉映,更加璀璨夺目.
