非搅拌膜反应器模型的稳定性和Hopf分岔

兰州交通大学数理学院 张 攀

一、引言

文献[1]中考虑了下面的具有齐次Neumann边界条件的非搅拌膜反应器的反应扩散系统：

引入下面的参数：

则模型（1.1）的反应扩散系统化简为：

下面我们引入反应扩散系统化成常微分系统的一般步骤：

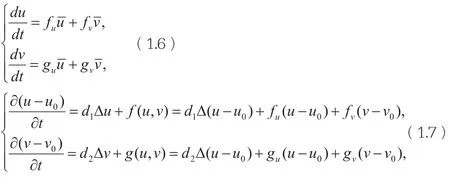
（1.8）为（1.1）的平衡解平移到原点后的系统。将该系统线性化，此时高阶项的扰动对系统的影响极小，我们可以将其忽略。

当没有扩散项影响时，Tang研究了系统（1.1）的全局动力学并给出了平衡点的分类。近来，通过构造适当的Lyapunov函数，Song和Tang研究了系统（1.1）正常数平衡解的全局渐进稳定性。

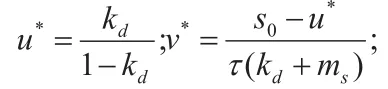
基于模型试验的桩周土压力·································张宇超 陆 烨 (2,296)

二、局部系统正常数平衡解的稳定性和Hopf分支

系统（1.1）所对应的常微分系统为：

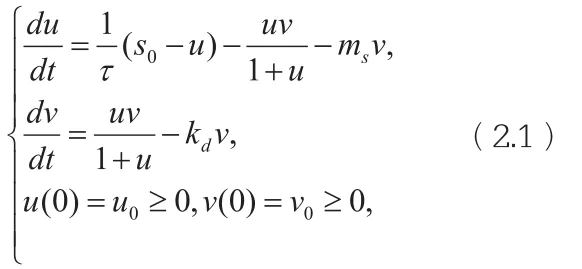
容易知道，如果

如果T＜0，那么系统（2.1）的正平衡点是局部渐近稳定的；

如果T＞0，那么系统（2.1）的正平衡点是不稳定的。

因此有如下结论：

定理2.1：假设上式条件成立，如果：