挖掘基本图形 培养数学核心素养
2018-02-22浙江省杭州市萧山区金山初级中学沈亚芳
浙江省杭州市萧山区金山初级中学 沈亚芳
近几年,杭州市的中考数学试题立足于数学基础,内涵丰富,既全面考查了学生的基本知识和解题基本技能,而且更加重视对学生的数学思想和数学基本图形的考查。重视学生发现问题、分析问题的能力,重视学生探究学习过程,促进学生进一步感悟问题的实质和数学思想方法。如2013年杭州市中考数学第二十三题以正方形为基本图形与图形的对称为外显形式,以动点为载体,试题立足于常规,为每一位教师的教学理念和教学目标指明了方向。本文站在八年级学生的视角以该题为例运用了旋转思想解题,解决了看似只有九年级学生才能挑战的中考压轴题。并对原题结论进行开发,凸显数学在再创造条件下的魅力。
一、原题再现,认识经典
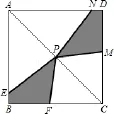
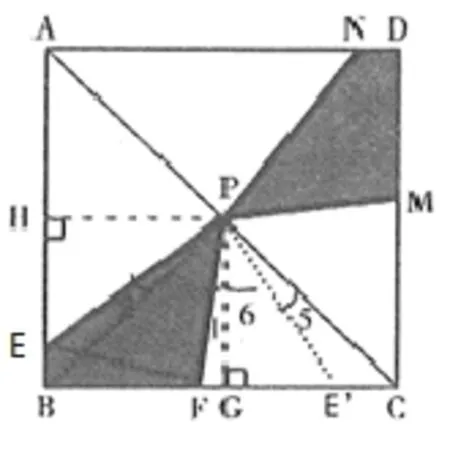
题1:如图,已知正方形ABCD的边长为4,对称中心为点P,点F为BC边上一个动点,点E在AB边上,且满足条件∠EPF=45°,图中两块阴影部分图形关于直线AC成轴对称,设它们的面积和为S1。
(1)求证:∠APE=∠CFP;
(2)设四边形CMPF的面积为
①求y关于x的函数解析式和自变量x的取值范围,并求出y的最大值;
②当图中两块阴影部分图形关于点P成中心对称时,求y的值。
【评析】本题是代数与几何综合题,考查了正方形的性质、几何变换(轴对称与中心对称)、相似三角形、二次函数解析式与最值、图形面积的计算等知识点,涉及的考点比较多且有一定的难度。本题的重点与难点在于求出y与x的解析式,最终的难点落在用x表示线段AE或BE的长上,同时用配方法求函数的最值问题也不是对一个常规的整式配方,而是对一个分式进行配方。因此,涉及整体换元的思想也是一个难点,设置第(1)小题证明∠APE=∠CFP的目的,是能为第(2)小题找到相似三角形去解决问题做了预设台阶,有了这个桥梁,九年级的学生能较容易地想到用相似比去表示出线段AE的长度,进而联系到面积之间的关系,这是九年级学生的常规解法,是出题者对学生的知识本身和逻辑思维能力的考察的意图。
二、挖掘基本图形,挑战经典
对于八年级学生而言本题的第一小题挖掘的基本图形是几何里常用的三角相等基本模型。可按照以下思维导图具体展示:
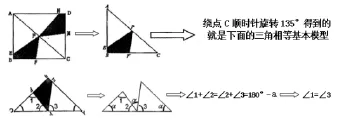
而本题的第二小题让八年级学生感到困难的应该是如何用好45°角,如何求一个不规则四边形的面积,求面积时如何表示出未知线段长度等,为帮助学生突破难点,笔者并不急于让学生解决原题,而是设计了一组问题串引导学生剖析背景图形和45°角进行探究,回溯以往的活动经验:
(1)正方形具备的性质是什么?通过作辅助线,可产生哪些45°角?
(2)E、F为线段AB,BC上的动点,则E和F的临界位置在哪?
(3)轴对称变换使得求阴影部分S1只需求什么?而对于不规则四边形求面积可用什么办法解决?
(4)无论是哪种办法,此题最重要的是求出哪些线段的长才可以表示出图形的面积?
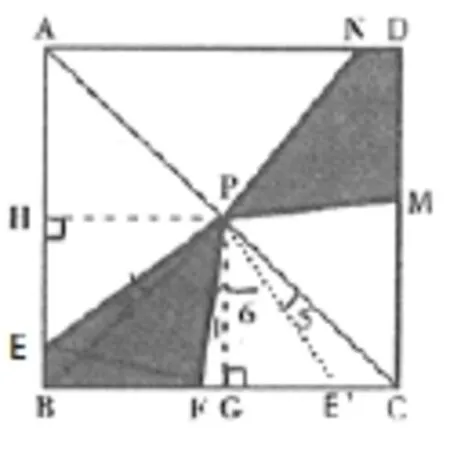
这样一步一步地追问和探讨已使问题简单明朗化,并在引导的过程中逐步添加出正方形中常用的辅助线,师生共同努力运用“旋转变换思想”获得了以下解法:巧用等腰RtΔPBC,拆分 45°角的基本模型。
题1(2)解:过点P作PH⊥BC于点C,连接BP,由正方形ABCD可知,∠APB=90°,∠BPG=45°=∠EPF,
即∠1+∠BPF=∠2+∠BPF, ∴∠1=∠2,
把△PEB绕点P顺时针旋转90°得到△PE'C,
则△PEB≌ △PE'C,∴BE=CE',∠2=∠5, ∴∠1=∠5,
∴∠1+∠6=∠5+∠6=∠CPG=45°,连接EF,易证△PEF≌△PE'F,则E'F=EF,
由FC=x,得出BF=4-x,∴E'F=BC-BF-CE'=4-(4-x)-BE=x-BE=EF,
在Rt△BEF中,由勾股定理可得,BE2+BF2=EF2,
【评析】这种解法违背了出题者的意图:利用正方形和等腰直角三角形完美的基本图形的本质特征,仅抓住隐含着的 45°和 90°角与题目所给的定角∠EPF=45°之间的关系,用旋转思想巧妙转化了线段与角之间的位置关系,又用方程思想将线段与线段之间的数量关系联系起来,使代数思想为几何所用。尤其是这种方法只涉及七、八年级的教材的知识,因此对其解法很有研究的价值。当学生们为自己利用八年级的知识就能解决中考压轴的最后一题时,对数学的兴趣和由此产生的成就感就不言而喻,从而激活他们的经验,提升他们的解题能力,有自信面对压轴题。
在刚刚考完的八年级期中考试中,最后压轴题中也有类似的基本图形。
题2:如图,在△ABC中,AB=BC,∠ABC=90°,D是AB上一动点,连接CD,点M是CD的中点,连接BM并延长交AC于点F,过D作DE⊥AC,垂足为E。
(1)当∠ACD∶∠BCD=2∶1 时,求证:①EM=BM;②EM⊥BF;③AE2+

(2)当点D在AB上移动时,(1)中的三个结论是否仍成立?(填“成立”与“不成立”即可)
①EM=BM_____;
②EM⊥BF______;
③AE2+CF2=EF2_____ 。
这里的第(2)小题③运用了和上题类似的运用旋转思想的等腰直角三角形基本模型。

由旋转得△BF’A≌△BFC,则∠BAF’=∠BCF=45°=∠BAC,FC=AF’,BF’=BF,∴∠EAF’=90°,由(1)的①②可知△BEM是等腰直角三角形,∴∠EBF=45°,从而∠EBF’=45°,再证△BF’E≌ △BFE(SAS), 推 得EF’=EF, 在 Rt△AEF’ 中,AE2+AF’2=EF’2,∴AE2+CF2=EF2,得证。
三、转化为基本图形,提升能力
题3:如图,长方形ABCD中,AD=10,AB=4,点Q是BC的中点,点P在AD边上运动,当△BPQ是等腰三角形时,AP的长为 。
每次碰到这个题目我都发现学生容易漏解,后来通过了解,发现学生都是凭直觉看看想想的,没有通过作图导致漏解。其实该题只要把它转化为基本作图:

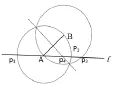
如图,已知直线l和A、B两点,在l上找一点P,使△ABP为等腰三角形的作法:分别以A、B为圆心,AB长为半径作圆,再过两圆交点作AB的中垂线,圆、中垂线和l的交点就是所求的P点。
而与上题类似的就是已知两点B,Q,在线段AD上找一点P,使△PBQ为等腰三角形的做法,学生只要有上面作图的想法就能把全部情况都找出来。
刚考过的期中卷上16题其实本质也是考等腰三角形的做法。只要想到两圆一线的做法,此题当然就不在话下了,只是重复作了3次而已:1.已知A,B在其余两边BC,AC上,找点P,使△ABP成为等腰三角形(可找到4个点);2.已知B,C在其余两边AB,AC上,找点P,使△BCP成为等腰三角形(可找到2个点);3.已知A,C在其余两边AB,BC上,找点P,使△ACP成为等腰三角形(可找到1个点),找完后把这些等腰三角形画出来后,7条线跃然纸上。
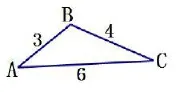
题目:如图,△ABC的边长分别为3,4,6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画____条。
四、探索新结论,培养更高素养
在解答完一个题目后教师可引导学生进行二次探索,能不能从已知中还可以得出新的结论,引发学生探究的欲望,久而久之,可以开拓学生思路,从而提高学生的数学思维品质和素养。
题1结论1:在点F的运动过程中,设△BEF的周长为C,则C的值是否变化?请证明你的结论。
分析:利用题1“旋转变换思想”得出的结论,
得C△BEF=BE+BF+EF=CE’+BF+E’F=4为定值,结论得证。
结论2:求证ΔPEF的面积等于EF的长。
分析:由图可知,ΔPE'F≌ΔPEF,则E'F=FE,则EF上的高,
即EF'上的高PH=2,即
五、反思结语
单纯地掌握几种方法和几个基本图形并不是我们学习数学的最终目的,更重要的是让学生对不同方法和不同的基本图形有所感悟和反思,从而对所学的知识做到融会贯通,深入浅出。原题的本意是第一小题证明角度相等为第二小题证明相似三角形铺路,从而利用对应边关系去寻求未知线段的表达式,事实上,此题的得分率并不高,学生在碰到新问题情境时仍然手足无措。所以教师在解题教学中需要立足数学的基础知识,让学生积淀数学活动经验,理解数学思想,抓住通法通性解题;对八年级学生而言,在学几何初期教师就要指导学生脚踏实地学好基本图形。对教师而言,可引导教师的教学回归原点,进一步对习题资源进行二次开发,引导学生把题目做出来后再深入反思。
学生在教师指导下的再创造学习,就是在回溯的前提下不断生成的过程,在题海中梳理表象,理清思维,凸显本质。相信长此以往,学生的数学核心素养就会像大树一样沐浴阳光,提升有度。
