可数仿紧空间和可数中紧空间的函数刻画
2018-02-20
(安徽工业大学数理科学与工程学院,安徽马鞍山243032)
Mack在文献[1]中证明了X为可数仿紧空间[2]当且仅当对X上的每一局部有界函数f,存在局部有界上半连续函数g使得|f|≤g;在文献[3]中,Mack证明了X为可数仿紧空间当且仅当对每一下半连续函数f>0,存在下半连续函数g及上半连续函数h使得0<g≤h≤f。Ohta等[4]证明了X为cb-空间当且仅当对任意递减函数列{fn∈U(X):n∈N}且fn→0,存在函数列{gn∈C(X):n∈N}使得对每一n∈N,fn≤gn且gn→0。作为对这一结论的推广,Yang在文献[5]中证明了关于可数仿紧空间,可数中紧空间[6]和可数亚紧空间的一些类似结果。例如,X为可数仿紧空间当且仅当对任一递减函数列{fn∈U(X):n∈N}且fn→0,存在函数列{gn∈L(X):n∈N},使得对每一n∈N,fn≤gn且{gn:n∈N}弱局部一致收敛于0。
文中引入k-上有界函数的概念,并利用k-上有界函数给出对可数中紧空间的一个类似的等价刻画。
1 预备知识
空间X的子集族G称为局部有限族,若X中的任一点有一个开邻域仅与G中有限多个元相交;称G为紧有限族,若X的任一紧集至多与G的有限多个元相交。
定义1X称为可数仿紧空间(可数中紧空间),若X的每一个可数开覆盖有局部有限(紧有限)开加细。
设X为拓扑空间,用0表示X上取值为0的常值函数。设{fn:n∈N}为空间X上的实值函数列,用fn→f表示{fn:n∈N}点态收敛于f。
空间X上的实值函数f称为下(上)半连续的,若对任意r∈R,集合{x∈X:f(x)>r}({x∈X:f(x)<r})为X的开集。若对X的任一紧集K,f在K上有最小值,则称f为k-下半连续函数。用L(X)(U(X),KL(X))表示从X到单位闭区间[0,1]的所有下(上,k-下)半连续函数的集合,UKL(X)=U(X)∩KL(X),C(X)为从X到单位闭区间[0,1]的所有连续函数的集合,L+(X)={h∈L(X):h>0}。
称空间X上的实值函数f在X上上有界,若存在n∈N使得对任意x∈X,f(x)≤n。若f在X的任一紧子集K上上有界,则称f为k-上有界函数。若对任意x∈X,存在x的开邻域U及n∈N,使得对任意x'∈U,有f(x')≤n,则称f为局部上有界函数。显然上半连续函数为局部上有界函数。
设X为拓扑空间,A⊂X,用IA表示A的特征函数,即对任意x∈X,
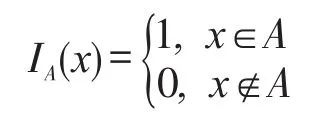
由特征函数的定义易得:若A为X的闭集,则IA上半连续;若A为X的开集,则IA下半连续。
2 可数仿紧空间
引理1[7]X为可数仿紧空间当且仅当对X中任一递减的且交为空集的闭集列{Fn:n∈N},存在X的递减的开集列{Un:n∈N},使得对每一。
Yang在文献[5]中证明了X为可数仿紧空间当且仅当对任一递减函数列{fn∈U(X):n∈N}且fn→0,存在函数列{gn∈L(X):n∈N},使得对每一n∈N,fn≤gn且{gn:n∈N}弱局部一致收敛于0。定理1表明函数列{gn:n∈N}可以用两个半连续函数列代替。
定理1X为可数仿紧空间当且仅当对任一递减的函数列{fn∈U(X):n∈N}且fn→0,存在函数列{gn∈L(X):n∈N}和{hn∈U(X):n∈N},使得对每一n∈N,fn≤gn≤hn且hn→0。
证明设X为可数仿紧空间,{fn∈U(X):n∈N}且fn→0。对每一n,k∈N,令,则对任意k∈N,{Fnk:n∈N}为递减闭集列且。由引理1知,对每一k∈N,存在X的递减的开集列{Unk:n∈N}使得Fnk⊂Unk且。对每一n∈N,令
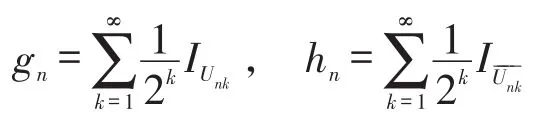
则gn∈L(X),hn∈U(X)且gn≤hn。
对每一n∈N及x∈X,若fn(x)=0,则fn(x)≤gn(x);若fn(x)>0,则存在k∈N 使得,故,则
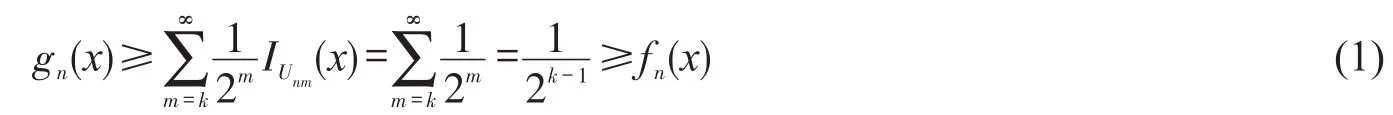
设x∈X,ε>0,取k∈N 使得。由于对每一i≤k,,故存在m∈N 使得对任意n≥m,ii令m=max{mi:i≤k},则对每一故对每一n≥m,

故hn→0。
反之,设{Fn:n∈N}为X中递减且交为空集的闭集列。对每一n∈N,令,则{fn∈U(X):n∈N}为递减函数列且fn→0。由条件知,存在函数列{gn∈L(X):n∈N}和{hn∈U(X):n∈N}使得对每一n∈N,fn≤gn≤hn且hn→0。对每一n∈N,令则Un为开集,Hn为闭集,且Fn⊂Un⊂Hn,因此Un⊂Hn。
设x∈X,由于hn(x)→0,故存在m∈N使得,由Hm的定义知,故。由引理1得X为可数仿紧空间。
利用定理1,可给出定理2的另一种证法。
定理2[8]X为可数仿紧空间当且仅当对每一h∈L+(X),存在φ(h)∈L(X)及φ(h)∈U(X),使0<φ(h)≤φ(h)<h。
证明设X为可数仿紧空间,h∈L+(X)。对每一n∈N,令则 {F(n,h):n∈N} 为X的递减且交为空集的闭集列。对每一n∈N,令f(n,h)=IF(n,h),则{f(n,h)∈U(X):n∈N} 递减且f(n,h)→0。由定理1,存在函数列{g(n,h)∈L(X):n∈N}及{l(n,h)∈U(X):n∈N}使得对每一n∈N,f(n,h)≤g(n,h)≤l(n,h)且l(n,h)→0,令
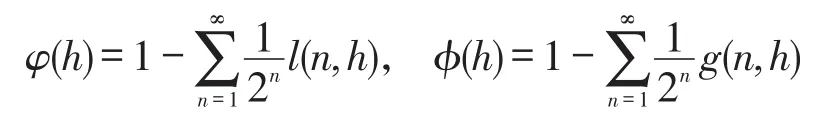
则φ(h)∈L(X),φ(h)∈U(X)且φ(h)≤φ(h)。
设x∈X,由于l(n,h)(x)→0,故存在m∈N使得l(m,h)(x)<1,故


反之,设{Fn:n∈N}为X的递减且交为空集的闭集列。令
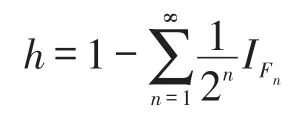
则h∈L+(X)。对每一n∈N,令
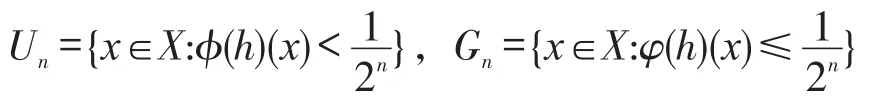
则Un为开集,Gn为闭集且Un⊂Gn,故Un⊂Gn。由于φ(h)>0,故,从而。设x∈Fn,令k=max{n∈N:x∈Fn},则n≤k,故
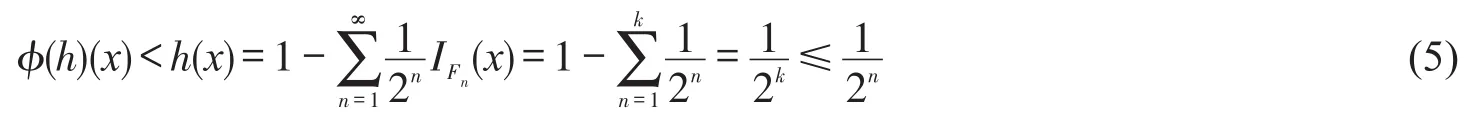
故x∈Un,从而Fn⊂Un。由引理1知,X为可数仿紧空间。
3 可数中紧空间
引理2[9]X为可数中紧空间当且仅当对X的任意递减且交为空集的闭集列{Fn:n∈N},存在X的递减开集列{Un:n∈N} 使得对每一n∈N,Fn⊂Un且对X的任一紧集K,存在m∈N使得K⋂Um=∅。
定理3对空间X,下列等价:
(a)X为可数中紧空间。
(b)对X上的每一局部上有界函数f,存在下半连续且k-上有界函数φ(f),使得f≤φ(f)。
(c)对X上的每一上半连续函数f,存在下半连续且k-上有界函数φ(f),使得f≤φ(f)。
(d)对X上的每一上半连续函数f,存在下半连续函数φ(f)及k-上有界函数φ(f),使得f≤φ(f)≤φ(f)。
证明(a)⇒(b)设X为可数中紧空间,对每一局部上有界函数f及n∈N,令则{Fn:n∈N} 为X的递减且交为空集的闭集列。由引理2,存在递减开集列{Un:n∈N} 使得对每一n∈N,Fn⊂Un且对任一紧集K,存在m∈N使得K⋂Um=∅。设U0=X。对每一x∈X,令nx=min{n∈N:x∉Un},φ(f)(x)=nx。设x∈X,由nx的定义知x∉Unx⊃Fnx,故f(x)≤nx=φ(f)(x)。
设x∈X,r∈R 且φ(f)(x)>r。令Ox=Unx-1,则Ox为x的开邻域。若x'∈Ox,则nx'>nx-1,故φ(f)(x')=nx'≥nx=φ(f)(x)>r,表明Ox⊂{x∈X:φ(f)(x)>r},从而φ(f)下半连续。
设K为X的紧集,则存在m∈N使得K⋂Um=∅,则对每一x∈K,x∉Um。由nx的定义得φ(f)(x)=nx≤m,因此φ(f)在K上上有界。
(b)⇒(c)显然,因为上半连续函数为局部上有界函数。
(c)⇒ (d)对每一上半连续函数f,令φ(f)=φ(f)。
(d)⇒ (a)设{Fn:n∈N} 为X的递减且交为空集的闭集列。对每一x∈X,令nx=min{n∈N:x∉Fn},f(x)=nx。下说明f上半连续。
设x∈X,r∈R 且f(x)<r。令Ox=XFnx,则Ox为x的开邻域。对任意x'∈Ox,由nx'的定义知nx'≤nx。因此f(x')=nx'≤nx=f(x)<r,这表明Ox⊂{x∈X:f(x)>r},因此f上半连续。
设φ(f),φ(f)为满足条件(d)的函数。对每一n∈N,令Un={x∈X:φ(f)(x)>n} ,则{Un:n∈N} 是X的递减的开集列。设n∈N,若x∈Fn,则n+1≤nx=f(x)≤φ(f)(x),故x∈Un,从而Fn⊂Un。设K为X的紧集,由于φ(f)在K上上有界,故存在m∈N使得对任意x∈K,φ(f)(x)≤m,故φ(f)(x)≤φ(f)(x)≤m,于是K⋂Um=∅。由引理2知X为可数中紧空间。
定理4表明,定理3(b)(c)(d)中的k-上有界函数可换为k-上半连续函数。
定理4对空间X,下列等价:
(a)X为可数中紧空间。
(b)对每一局部上有界函数f,存在下半连续且k-上半连续函数φ(f),得f≤φ(f)。
(c)对每一上半连续函数f,存在下半连续且k-上半连续函数φ(f),得f≤φ(f)。
(d)对每一上半连续函数f,存在下半连续函数φ(f)且k-上半连续函数φ(f),使得f≤φ(f)≤φ(f)。
证明(a)⇒(b)设X为可数中紧空间,对每一局部上有界函数f,设φ(f)为定理3的(a)⇒(b)证明过程中定义的函数,则只需说明φ(f)k-上半连续。设K为X的紧集,则存在n∈N使得K⋂Un=∅。令m=min{n∈N:K⋂Un=∅ },则。取,则且对任意x∈K,nx≤m。因此,所以φ(f)k-上半连续。
(b)⇒(c)及(c)⇒(d)显然。
(d)⇒(a)设(d)成立,由于k-上半连续函数为k-上有界函数,由定理3(d)⇒(a)知X为可数中紧空间。
定理5对空间X,下列等价
(a)X为可数中紧空间。
(b)对任意h∈L+(X),存在φ(h)∈UKL(X)使得 0<φ(h)<h[9]。
(c)对任意h∈L+(X),存在φ(h)∈U(X)及φ(h)∈KL(X)使得 0<φ(h)≤φ(h)<h。
证明(a)⇒(b)在文献[9]中已证,此处给出另一种证明方法。
设X为可数中紧空间,对每一h∈L+(X)及n∈N,令,则{F(n,h):n∈N} 为X的递减且交为空集的闭集列。由引理2,存在X的递减开集列{U(n,h):n∈N} 使得对每一n∈N,F(n,h)⊂U(n,h)且对X的任一紧集K,存在m∈N使得K⋂U(m,h)=∅。令
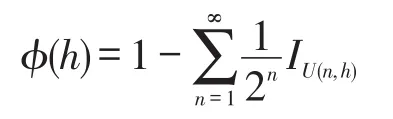
则φ(h)∈U(X)。对每一x∈X,存在m∈N 使得x∉U(m,h)。令k=min{n∈N:x∉U(n,h)},则对任意n≥k,x∉U(n,h)且对每一n<k,x∈U(n,h)。由于x∉U(k,h)⊃F(k,h),故,因此

设K为X的紧集,则存在m∈N使得K⋂U(m,h)=∅。令k=min{n∈N:K⋂U(n,h)=∅ },则K⋂U(k-1,h)≠∅ 且对每一n≥k,K⋂U(n,h)=∅。取x0∈K⋂U(k-1,h),则对每一n≥k,x0∉U(n,h)且对每一n<k,x0∈U(n,h),从而。对每一x∈K,
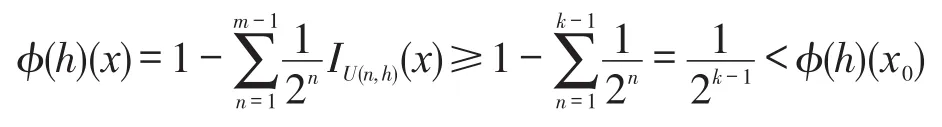
从而φ(h)∈KL(X)。
(b)⇒(c)显然。
(c)⇒(a)设{Fn:n∈N} 为X的递减且交为空集的闭集列,令
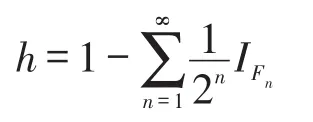
则h∈L+(X)。对每一n∈N,令,则Un为开集。设x∈Fn,令k=max{n∈N:x∈Fn},则n≤k,从而
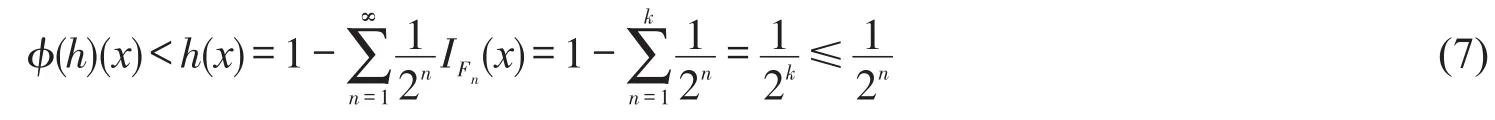
表明x∈Un故Fn⊂Un。设K为X的紧集,由于φ(h)∈KL(X),故存在x0∈K使得对任意x∈K,φ(h)(x)≥φ(h)(x0)。由于φ(h)(x0)>0,故存在m∈N,使得,故对任意x∈K,有,表明K⋂U(m,h)=∅。由引理2知X为可数中紧空间。
