倾斜角与斜率

山东省聊城市高唐县高唐二中学校 刘艳军

一、教学目标

1.在平面直角坐标系中，结合具体图形，探索确定直线位置的几何要素。

2.理解直线的倾斜角和斜率的概念，经历用代数方法刻画直线斜率的过程，掌握过两点的直线斜率的计算公式。

3.体会数形结合及分类讨论思想在概念形成及公式推导中的作用。

重点：斜率的概念，用代数方法刻画直线斜率的过程，过两点的直线斜率的计算公式。

难点：直线的斜率和倾斜角之间的关系，即用代数方法推导斜率的过程。

二、教学过程

（一）创设情境，揭示课题

问题1、（出示幻灯片）给出的两点P、Q相同吗？

从形的角度看，它们有位置之分，但无大小与形状之分。

从数的角度看，如何区分两个点？（用坐标区分）

问题2、过这两点可作什么图形？唯一吗？只经过其中一点（如点P）可作多少条直线？它们的区别用什么来刻画呢？

若只想定出其中的一条直线，除了再用一点外，还有其他方法吗？可以增加一个什么样的几何量？（估计不少学生能意识到需要有一个角）

由此引导学生归纳，确定直线位置可有两种方式

（1）已知直线上两点

（2）已知直线上一点和直线的倾斜程度

问题3、角的形成还需一条线，也就是说要有刻画倾斜程度的角，就必须还有一条形成角的参照的直线。在平面直角坐标系下，以哪条轴线为基准形成刻画倾斜程度的角？（学生可能回答x轴或y轴）

以x轴或y轴为基准都可以，习惯上我们用x轴。

问题4、过点P与x轴形成450角的直线有几条？

（学生可能答一条或两条，投影演示结果）如何区分清楚这两条直线呢？估计学生能想到还需要确定方向。

选择哪个角来描述直线的倾斜程度，就能保证坐标系下的任何一条直线都有唯一的角与它对应呢？

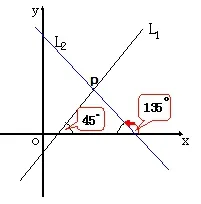
（教师引导学生选取不同的方向来描述角，并区分L1与L2）。

数学概念来刻画事物时，讲求统一美与简洁美，如何用数学语言准确描述这个角呢？（揭示课题）

1.倾斜角的定义：在直角坐标系下，以x轴为基准，当直线l与x轴相交时，x轴正向与直线l向上方向之间所成的角α，叫做直线l的倾斜角。

学生练习画出过点P的各种倾斜角的直线。

学生容易忽略与x轴平行的直线，补出图（4），问倾斜角在哪儿？如何规定？

规定：当直线l与c轴平行或重合时，它的倾斜角为0°。

（1）讨论一下几个问题

①直线倾斜角的范围是多少？

②在平面直角坐标系中，每一条直线都有确定的倾斜角吗？

③倾斜角相同的直线相同吗？

自然有倾斜角的范围是[0°，180°）

这样平面直角坐标系中每条直线都有唯一一个确定的倾斜角α与它对应。倾斜程度相同的直线，其倾斜角相等，倾斜程度不同的直线，其倾斜角不相等。

以上定义了一个从“形”的角度用倾斜角刻画平面直角坐标系内一条直线的倾斜程度。

（二）巩固旧知，同化新知

生活中，我们都有过爬山、爬坡的体验，对于斜坡的倾斜程度，可以用什么量来反映？（坡角与坡度）初中对坡度是如何定义的？

当坡角α增大时，坡度如何变化？

当坡角α=90°与0°时，升高量、前进量分别是什么？坡度又分别是什么？

坡角、坡度都能反映倾斜程度，迁移到数学中，坡角相当于直线的倾斜角，而坡度则对应于直线的斜率。

2.斜率：倾斜角不是90°的直线，其倾斜角的正切值叫做这条直线的斜率。即k= t an α ( α ≠ 9 0°)

问题5、当α为钝角时，直线的斜率如何求？（转化到其补角θ上）

问题6、当α在[0°，180°）内变化时，斜率k如何变化？

问题7、倾斜角与斜率都能刻画直线的倾斜程度，哪个量更优越呢？

倾斜角能从形的角度刻画倾斜程度，而斜率是比值，实质是数值，它能从数的角度反映倾斜的程度，显然用斜率更细致入微些。

（三）尝试推导，深化认识

两点确定一条直线，可见由两点也就确定了直线的倾斜程度，即倾斜角与斜率。看来，直线上两点与直线的斜率有着密不可分的联系。

问题8、在平面直角坐标系中，已知直线上两点P1（x1，y1），P2（x2，y2）且x1≠x2，能否用P1、P2的坐标来表示直线斜率k？

（学生活动）：随意在坐标系下画两点P1、P2及直线P1P2，探究各种图形并尝试推导，可以先特殊再一般，也可先一般再特殊地去分析。教师可适当引导其将斜坡截面图迁移到坐标系中，类似升高量，前进量，用点的坐标表示线段长，并请同学叙述各个图的推导过程与结果。

解：设直线P1P2倾斜角为α（α≠ 9 0°）当直线P1P2方向向上时，过点P1作 轴的平行线，过点P2作 轴的平行线，两线交于点Q，则点Q为（x2，y1）

（1）当α 为锐角时，α=∠QP1P2，x1＜x2，y1＜y2

在RtΔP1P2Q中，

（2）当α 为钝角时，α = 1 80°-θ（设∠QP1P2=θ），x1＜x2，y1＜y2,tan α = t an(180°- θ ) = -tan θ

在RtΔP1P2Q中，（可让学生分组推导）

同理，当直线P2P1方向向上时，无论α为锐角或钝角，也有即

思考：1、各种一般情形得出的结论一致吗？与P1、P2这两点坐标顺序有关系吗？

2、当直线垂直于x轴或y轴时，上述结论适用吗？

3、斜率公式使用时应注意什么问题？

巩固练习：求经过下列两点直线的斜率，并判断倾斜角是锐角还是钝角。

（2）A（3,2）,B（4,1）（kAB=-1）

（3）A（3,2）,B（3,-1）（不存在）

（4）A（3,2）,B（-4,2）（kAB=0）

（四）反思小结，概括提炼（同学们这节课有何收获？）

1.明确了确定直线位置的几何要素。

2.理解了刻画倾斜程度的量（倾斜角与斜率），知道了求斜率的两种方法（定义法、坐标法）

3.经历了代数方法刻画斜率的过程,感受了数形结合与分类讨论的数学思想

(五)板书设计

（六）作业

①自学课本 P85：例1、例2；

②作业本： P89：1、2、3。