穿过非穿越 分类来把舵

刘兵

【摘要】 本文主要采用分类讨论的思想方法探索正方形ABCD向右水平移动的过程中，与右边一固定的正方形EFGH重合部分的面积S，如何用时间t的函数关系式表达的问题.

【关键词】 分类讨论;函数思想;临界状态

几何图形的运动变化一直以来都是中考命题专家青睐的热点，这一类题目在编写时都在不同程度上体现出基本图形、基本概念来源于现实生活，将现实生活中的一些问题抽象化得到.这类题型注重培养学生良好的观察、操作、想象、讨论、交流等学习习惯，在“数学模型——绘出图形——文字描述——符号表达”抽象化的一系列过程中，提高学生顺向、逆向相互转化的思维能力，让学生立足于基础知识，加强知识间横向與纵向、内在与外在、具象与抽象之间的联系.

学生在吸收知识的同时更应该领悟其中蕴含的基本数学思想，并能进行适度的提炼和总结，使之能对认识能力、理解能力和应用能力发挥指导作用，更好地理解数学实质，初步具有数学思维能力.

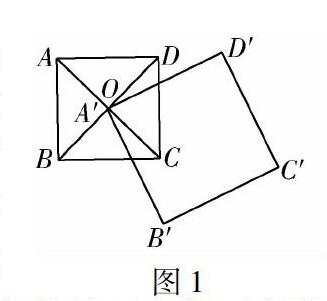
笔者在给学生讲解四边形的知识时，碰到了一道边长不相等的两个正方形组合的问题.其中大的正方形A′B′C′D′的一个顶点A′与小正方形的中心O重合，并围绕小正方形ABCD的中心O旋转，无论如何旋转，它们重合部分的面积都不变的有趣问题（如图1所示）.

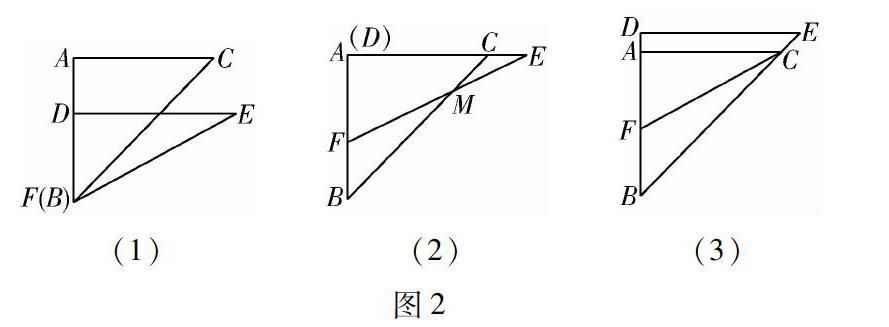
如图2（1）所示，将三角板DEF固定不动，现三角板ABC沿射线DB方向平行向下移动.当点A运动到与点D重合时停止，BC与EF相交于点M（如图2（2）所示）.先观察重合部分四边形ACMF的形状，再求出此时重合部分四边形ACMF的面积.

如图2（3）所示，将三角板ABC继续向下运动，当点A运动到与点F重合时立即停下来.设DA=x cm，重合部分的面积为y cm2.求在此运动过程中y cm2和x cm的关系式，并求出对应的x的取值范围.

（1）

（2）

（3）

受此启发，我们将图1中不相同的两个正方形都变为边长相同的正方形，并作如下规定：

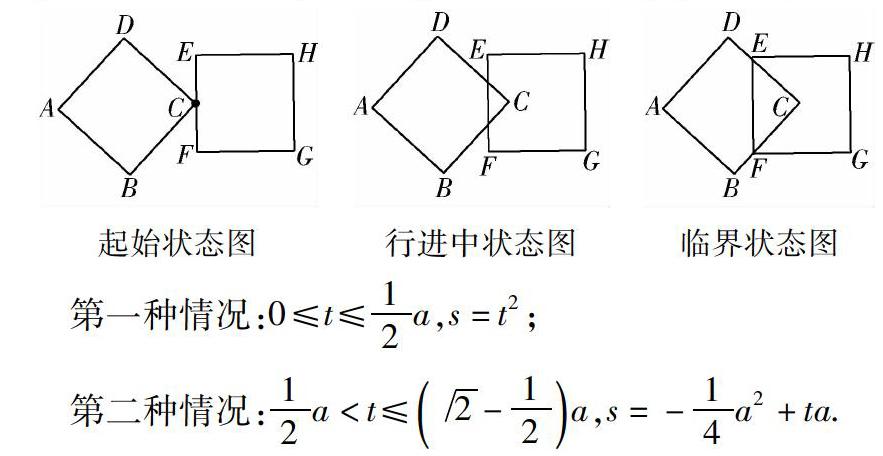
设边长为a的相同正方形，按如图所示的方式放置，右边正方形EFGH是水平放置，其中∠BCF=45°，C是EF的中点（左边正方形的右边顶点与右边正方形的边所在的中点重合），同时令左边正方形水平向右按每秒一个单位长度的速度平移，右边正方形EFGH固定不动.请你计算从左边正方形ABCD开始进入直至完全穿过并离开右边正方形EFGH时两正方形重合部分的面积S与运动时间t（初始状态时t=0秒）之间的函数关系，并求出对应的t的取值范围.

下面我们就按照刚刚叙述的方法分为八种不同的情况进行梳理解答.首先呈现移动变化过程中关键位置的三种状态图，再根据此种情况下“行进中状态图”来计算重叠部分的面积与时间t（初始状态时t=0秒）的函数关系.

第一种情况：0≤t≤ 1 2 a，s=t2;

第二种情况： 1 2 a<t≤  2 - 1 2  a，s=- 1 4 a2+ta.

从第一种情形到第二种情形的解答全部过程，明确地反映出了从正方形ABCD开始进入直至完全穿过并离开正方形EFGH时两正方形重合部分的面积与运动时间t（初始状态时t=0秒）之间的函数关系.

本体可以赋予特殊化的表现形式，现列举如下：

特殊情形1  题目要求、图形同上.当边长a=6时，请你计算从左边正方形ABCD开始进入直至完全穿过并离开右边正方形EFGH时两正方形重合部分的面积S与运动时间t（初始状态时t=0秒）之间的函数关系，并求出对应的t的取值范围;并计算t为何值时，重合部分的面积S最大，最大值是多少.

特殊情形2  题目要求、图形同特殊情形1，边长a=6.正方形ABCD的运动速度按每秒一个单位长度的速度平移，右边正方形EFGH按每秒0.5个单位长度的速度向右水平移动.请你计算从左边正方形ABCD开始进入直至完全穿过并离开右边正方形EFGH时两正方形重合部分的面积S与运动时间t（初始状态时t=0秒）之间的函数关系，并求出对应的t的取值范围.

本题特殊情形都属于操作类试题，题目的情境设置很平常，仅仅运用了学生熟悉的素材、熟悉的知识、熟悉的解 题方式命制出一道综合多个知识点且充满挑战的问题，化平常为神奇，考查了学生的基础知识、基 本技能和基本数学方法.

【参考文献】

[1]邓凯.广东卷第25题：用一副三角板创编的好题[J].中学数学教学参考：中旬，2013（8）：55-57.