巧用函数思想，妙解数学问题

沈桂兰

【摘 要】 在数学教学中，教师要注意有效渗透函数思想，巧妙地运用函数定义、性质、图象、值域等函数思想载体去分析、转化和解决问题，从而使问题得以快速、巧妙、准确、有效地解决。

【关键词】 巧用；函数思想；数学；问题

函数思想是数学解题中至关重要的思想方法，它涉及知识点多，覆盖面广，综合应用强，解法灵活多样，对于培养学生思维深刻性、灵活性和创造性，提升学生思维品质，培养学生良好数学素养有着积极的作用。对此，笔者从自身教学实践出发，就如何在数学教学中引导学生巧用函数思想妙解数学问题略谈了如下看法，以供参考。

一、利用函数定义，有效解决数学问题

函数的基本定义是：设A、B是非空数集，若根据某个确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数f（x）和它对应，那么就称f：A→B为从集合A到集合B的一个函数，记作y=f（x），x∈A.其中x叫做自变量，x的取值范围A叫做函数的定义域；与x的值相对应的y值叫做函数值，函数值的集合{f（x）|x∈A}叫做函数的值域。

函数定义是学生学习和掌握函数知识的重要基础。灵活运用函数定义解决数学问题，既可以深化学生对函数概念的理解，又可以提高学生应用函数定义解题意识，发展学生的思维能力。许多学生在解函数问题时感觉束手无策、无从下手，究其主要原因是学生对函数定义理解不透彻、把握不当，因此，在平时教学中，教师要注意强化函数概念，增强学生解题能力。

例1 若f（x）与g（x）都是定义在R实数集上的函数，且方程x-f[g（x）]=0有实数解。则g[f（x）]不可能为（ ）.

A.x2-1/5 B. x2+1/5 C. x2+x-1/5 D. x2+x+1/5

解析：此题乍看之下学生可能无从下手，但若能结合函数定义，则可使问题豁然开朗起来。方程x-f[g（x）]=0有实数解，设解为a，将其代入得a-f[g（a）]=0，把方程看成函数，这样a-f[g（a）]=0可理解成在g（x）定义域中存在元素a经过映射g，设对应的象为b， b经过映射f后，在f（x）的值域中存在a与之相对应。这样对于g[f（x）]而言，函数定义可知存在b，使得g[f（b）]=b成立，即方程g[f（x）]=x有解，将上述选项中的答案逐一代入进行验证，可知g[f（x）]不可能为x2+x+1/5，故应选D.

例2 已知集合M={a， b， c}，N={-2，0，2}，求建立从M到N且满足f（a）+f（b）+f（c）=0的函数f个数。

解析：许多学生在解答本题时，往往束手无策，不知如何下手。事实上，本题的解题突破口是正确理解f（a）+f（b）+f（c）=0这一函数。根据函数的基本定义，不难发现，f（a），f（b），f（c）三个函数均是属于集合N中的元素，因而此题可以转化为从N中可任意取3个元素（可重复）满足f（a）+f（b）+f（c）=0这一已知条件。由于每个式子对应着一个函数关系，又由于f（a）+f（b）+f（c）=0的表达式仅有0+0+0=0或-2+0+2=0，因此，满足题意要求的函数f个数为：A33+1=7.

点评：在解某些数学问题的过程中，灵活巧妙地运用函数定义解题，往往可以收到事半功倍的效果。

二、把握函数性质，灵活解决数学问题

函数基本性质主要包括了函数的奇偶性、单调性、周期性、对称性等方面。在解某些问题时，若能善于挖掘问题的隐含条件，有效构造函数，灵活巧妙地运用函数性质，往往可以达到化繁为简，化难为易的目的，从而使问题迎刃而解。因此，在平时函数教学中，教师要注意引导学生正确理解函数性质，把握好函数内涵外延和本质特征，为数学解题奠定良好的基础。

例3 设x， y∈[-π/4，π/4]，a∈R，且x3+sinx-2a=0，4y3+sinycosy+a=0，求cos（x+2y）的值。

解析：此题若直接从三角变换角度进行分析和处理，往往难度较大，不易下手。但若能变换视角，转变思路，将两个方程变形为：x3+sinx=2a ①；（-2y）3+sin（-2y）=2a ②；结合两方程结构特征，可构造函数f（a）= a3+sina，联立方程①②可得f（x）=f（-2y）.而f（a）在[-π/2，π/2]上单调递增，故x=-2y x+2y=0 cos（x+2y）=1.

点评：对于有些数学问题，条件中有时给出的是不具备特殊性质的函数，此时若构造适当的函数，将条件适当变形，再巧用函数性质解题，往往会使问题“柳暗花明”，得以轻松获解。

三、结合函数图象，轻松解决数学问题

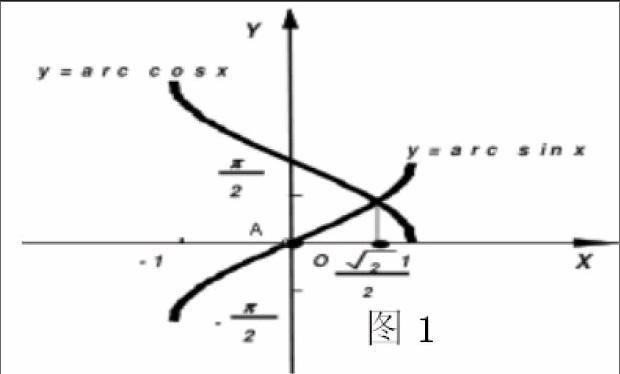
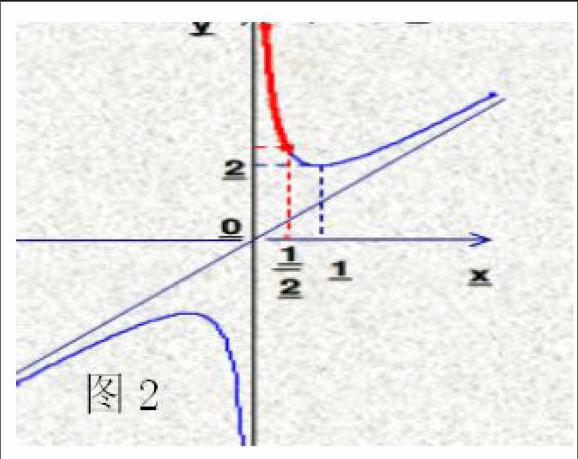
函数图象是函数的基本表达形式之一，是研究和表述函数的重要工具，它将函数的变化趋势直观化，以图形的形式直观地展现函数的性质特征，借助函数图象的直观性解题，可以简化解题过程，使问题得以轻松获解。

由x>0得a≥-（x+1/x）对于0

点评：巧妙地结合函数图象分析和解决数学问题，往往可以使一些看似复杂的问题变得简单化，从而迅速找到问题的突破口，巧妙求解。

总之，函数思想贯穿于数学教学中，具有一定的广泛性、多样性、灵活性、创造性等特点。在平时教学中，教师应重视函数思想的有效渗透和灵活运用，引导学生充分挖掘数学问题中隐含的函数思想，学会巧用函数概念、性质、图象来分析、转化和解决问题，从而帮助学生掌握函数思想，提升学生思维品质，增强学生数学解题能力。

【参考文献】

[1]龙婷.运用函数思想解数列问题[J].中学生数学 2015年21期

[2]吴丽华.浅谈函数思想在数列中的应用[J].中学数学 2015年21期

[3]许钦彪.例谈函数问题在数学中的意义和作用[J].中学教研（数学）2015年11期

[4]龙婷.运用函数思想解数列问题[J].中学生数学 2015年21期