合理设计数学问题 培养学生高阶思维

管红娟

【摘要】 培养初中学生高阶思维能力，提升学生的思维品质，是每位数学教师的责任.课堂教学是教师的主阵地，如何运用这个阵地培养学生的高阶思维，是值得我们思考的问题.本文针对数学课堂问题的合理设计，用问题驱动学生，用问题引领学生，让学生的思维品质的深刻性、灵活性、创新性和批判性得以发展.

【关键词】 高阶思维;数学问题;合理设计

近年来，高阶思维成为初中数学的核心价值取向和教学目标的追求.高阶思维的概念源自美国心理学家本·杰明·布卢姆和罗伯特·加涅等人的理论.数学高阶思维，是指在数学活动中有意识的、围绕特定目标的、需要付出持续心理努力的高层次认知水平的复杂思维，它具有严谨性、深刻性、批判性、独创性和灵活性的特点.学生学好数学需要较强的高阶思维能力，如何培养学生的高阶思维能力是教学面临的问题.

数学课堂教学是思维活动的教学，而思维总是指向解决某个问题的，没有问题就不会有思维活动，从这个意义上说产生学习的根本原因是问题，问题是数学的心脏，是思维的起点，是学生主动探索的动力，是发展学生的认知结构，培养学生高阶思维品质的逻辑力量.

数学课堂教学中一个恰当的问题，有利于激发学生的学习兴趣，调动学生的积极性，会让学生思维的火花不停地跳跃.而如果抛出的问题过于“水平化”，思维会固步不前;如果问题过于“垂直化”，思维会割裂;问题过于“碎片化”，又不利于形成思维体系.如何利用课堂教学，培养学生的高阶思维，M.H马赫穆托夫的《问题教学》理论给我们提供了思路.创建问题情境，设计对话，预设合理的数学问题，引领学生完成学习目标，走向探索之路，完成高阶思维的培养.

一、设计“递进式”问题，促进思维的“深刻性”发展

“递进式”问题设计由易到难、由浅入深，循序渐进设计问题链，切合学生的实际认知水平，阶梯式上升，使得认知结构的“最近发展区”转化为“已知区”，实现由低层次思维到高阶思维的转换.

案例1  （沪科版八年级第一学期46页例题3第（1）问）

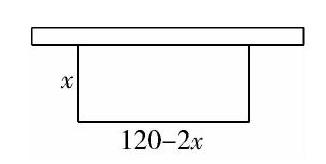
某建筑工程队，在工地的一边靠墙处，用120米长的铁皮围成一个所占地面为长方形的临时仓库，铁栅栏只为三边，按下列要求，分别求长方形的两条邻边长.（1）长方形的面积是1152平方米.

问题1 如果墙长82米.

问题2 如果墙长100米.

问题3 如果墙长52米.

问题4 如果墙长m米，问：m在什么范围时，围成长方形有两种情形、一种情形或不能围成长方形？请说明理由.

设计意图：前3个问题，学生在检验方程的根是否符合实际意义情况下，对墙长与长方形的长两者之间的关系逐步深入理解.问题4，学生在理解前3个问题的基础上，学会总结与概括.这样设计可以培养学生思维的深刻性，即逻辑性.思维的深刻性是一切思维品质的基础.思维的深刻性集中体现在善于深入思考问题，抓住问题的规律和本质，让思维“螺旋式”上升.

二、设计“一题多解”问题，促进思维的“灵活性”发展

“一题多解”，对于一个问题，可以有多个开端，产生许多联想，获得各种各样的想法.学生思维的灵活性实质是“迁移”.灵活性越大，发散思维越发达，越能多解，多解的类型越完整，组合分析的交叉点越多，说明这种迁移过程越显著.“举一反三”是高水平的“发散”，正是来自思维的灵活.

案例2  【2011中考】第24题

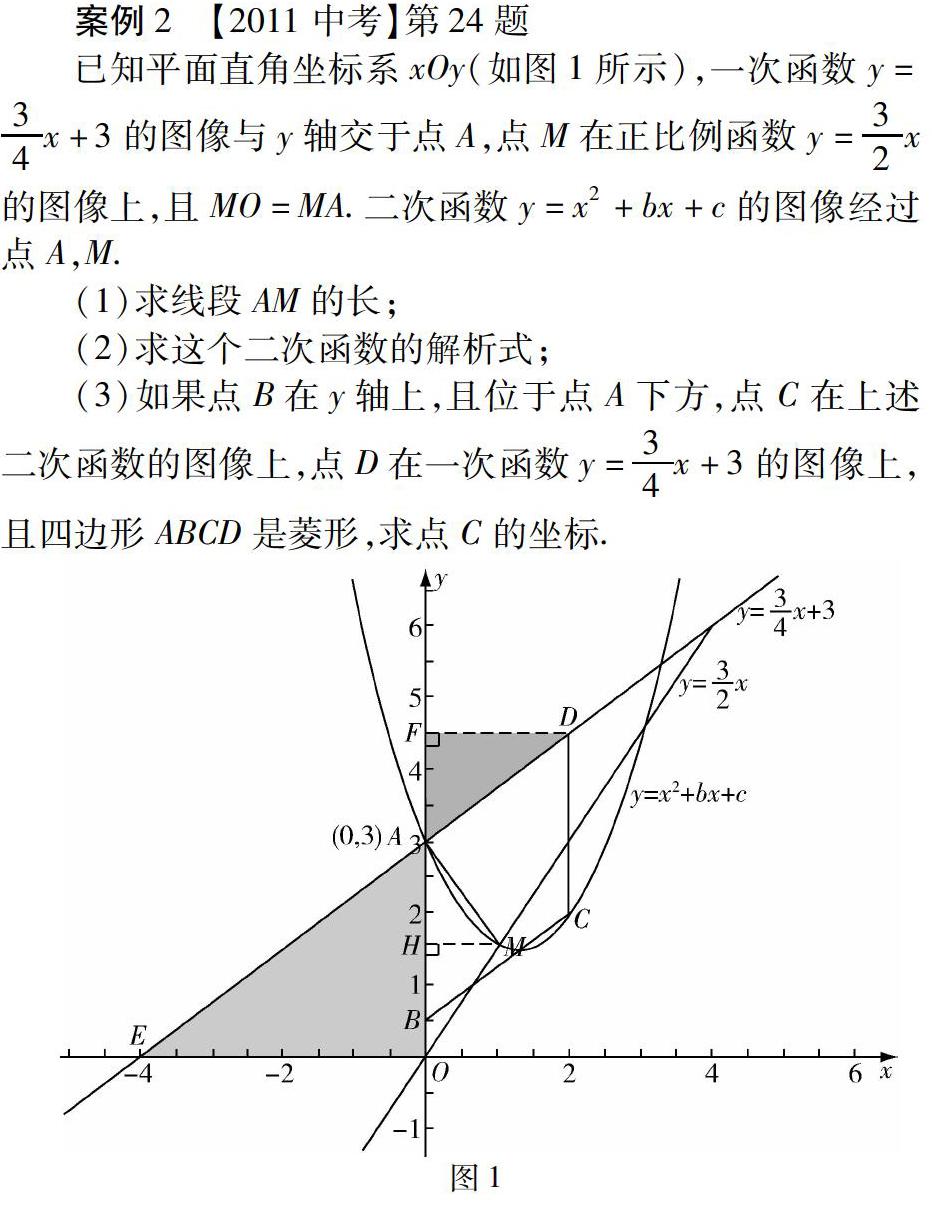
已知平面直角坐标系xOy（如图1所示），一次函数y= 3 4 x+3的图像与y轴交于點A，点M在正比例函数y= 3 2 x的图像上，且MO=MA.二次函数y=x2+bx+c的图像经过点A，M.

（1）求线段AM的长;

（2）求这个二次函数的解析式;

（3）如果点B在y轴上，且位于点A下方，点C在上述二次函数的图像上，点D在一次函数y= 3 4 x+3的图像上，且四边形ABCD是菱形，求点C的坐标.

分析：

第（1）问

（几何法）

问题1 看到MO=MA，你想到动点M的轨迹是什么？

问题2 如何作图？作线段AO中垂线与此二次函数图像的交点即为点M.

（代数法）

问题3 如果利用代数法，根据MO=MA，你能联想到什么知识点？根据两点之间的距离公式列方程.

第（3）问

问题1 点B在y轴上，起到什么作用？利用DC∥AB，DC=AB确定平行四边形ABCD.

（代数法）

问题2 运用代数法，利用菱形的性质，你找到了什么等量关系式？DA=DC列方程.

（几何法）

问题3 运用几何法，你准备构造什么基本图形？作 DF⊥ y轴于点F，设直线y= 3 4 x+3与x轴的交点为E，则DF∥OE，即“八”字图.

设计意图：菱形存在性的“两定两动”问题，涉及知识点有一次函数、二次函数的图像与应用、两点间的距离公式（勾股定理）、解一元一次方程、解二元一次方程组、菱形的判定与性质等;用到的数学思想方法有函数与方程思想、数形结合思想、转化思想.显然要求学生要学会灵活运用已学的数学知识，做到“触类旁通”，提升高阶思维的灵活性品质.

三、设计“开放性”问题，促进思维的“独创性”发展

开放性问题是指条件和结论不确定、解题策略多样化的题目.它一般需要学生通过观察、实验、估计、猜测、类比和归纳等才能解决，对学生具有挑战性和探究性.把开放性问题带入课堂，是提高课堂教学质量的有效途径，对培养学生的高阶思维有着重要作用.

案例3  如图2所示，二次函数y=ax2- 3 2 x+2（a≠0）的图像与x轴交于A，B两点，与y轴交于点C，已知点A（-4，0）.

（1）求抛物线与直线AC的函数解析式;

（2）若点D（m，n）是抛物线在第二象限的部分上的一动点，四边形OCDA的面积为S，求S关于m的函数关系式;

（3）若点E为抛物线上任意一点，点F为x轴上任意一点，当以A，C，E，F为顶点的四边形是平行四边形时，请直接写出满足条件的所有点E的坐标.

这是一道以二次函数为背景的四边形的面积和平行四边形存在性问题.

课堂教学完成以后，我们可以适时地将四边形问题深入，可以加上直角梯形存在性问题.此时，我们可以设计让学生编题，让思维发散开来.

问题1 △ABC是什么形状？直角三角形

问题2 是否存在一点G，使得以A，C，B，G为顶点的四边形是直角梯形？这样的点G有多少个？无数个

问题3 如果想定下来，那么点G可以落在什么位置，请自编一题.

设计意图：直角梯形存在性的“三定一动”问题，学生要完成它需系统地掌握直角梯形的性质和判定、函数与方程等综合類知识.只要问题设计合理，经过一段时间，可以提高一个年级的水平，同时思维独创性品质也得到了培养.

四、设计“思辨性”问题，促进思维的“批判性”发展

所谓“思辨性”问题，是指一些具有认知冲突的问题，能够引起学生对数学的思考、辨析，用理性的思考诠释智慧的申辩，从而提升学生的高阶思维的批判性品质.数学课堂就是我们的“训练场”，如何让学生在场地上充分得到训练，问题意识尤为重要.

总之，高阶思维能力的培养是一项复杂且系统的工程，我们要用好数学课堂这块“阵地”，设计具有层次性、探究性、开放性、思辨性等问题.利用这些问题，充分挖掘学生的能力，唤醒学生的思维意识，以问题引领深度思维，让师生的思维品质“比翼齐飞”.

【参考文献】

[1]朱智贤，林崇德.思维发展心理学[M].北京：北京师范大学出版社，1986.

[2]张奠宙，于波.数学教育的“中国道路”[M].上海：上海教育出版社，2013.

[3]曹才翰，章建跃.数学教育心理学[M].北京：北京师范大学出版社，1999.

[4]魏清.中学有效教学策略研究[M].上海：上海三联出版社，2005.

[5]宁连华.数学探究学习研究[D].南京：南京师范大学，2004.