概念图与小学数学概念教学

洪伟 程小红

【摘要】 概念图是一种实现知识可视化的工具，主要由概念和概念间的关系构成，基本构成单元是命题，具有清晰的层级结构.在小学数学概念教学中引入概念图可以较好地提升学习效果，其作用主要包括三个方面：帮助建构概念体系;实现陈述性知识向程序性知识的转化;突出知识本质，实现不同知识之间的关联.

【关键词】 概念图;小学数学;概念教学

概念图一词是由英文“concept map”翻译而来，其创始人是美国教育心理学家诺瓦克（Joseph D.Novak）教授.诺瓦克在其专著《学会学习》中指出概念图是指用命题的形式来表征不同概念间的有意义联系（的工具）;命题是指在一个语义单元中由连接词连接起来的两个或两个以上的概念名称;概念是指用于表示事物规律的名称.

由定义可以看出概念图在表现形式上具有如下特点：

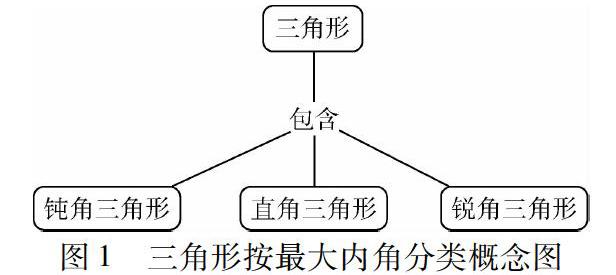
首先，其构成要素是概念和概念间的关系，表示概念的词放在方框或圆圈中并位于顶点的位置，相关的概念间用短线交叉连接，根据需要在交叉连接上标注是什么样的关系.例如，三角形按最大内角可分为钝角三角形、直角三角 形和锐角三角形，这句话可以用图1所示的概念图来表示：

其次，概念图的 基本构成单元是命题，如图1所示三角形、钝角三角形以及二者之间的交叉连接就构成了一个命题，含义是三角形包含钝角三角形或钝角三角形包含于三角 形.

第三，概念图具有清晰的层级结构.绘图时一般将上位概念写在图形的上方，如图1中的“三角形”;下位概念或从属概念放在图形的下方，如图1中的“钝角三角形”等;交叉连接表示两个概念间存在的某种关系.

从这些表现形式上的特点可以看出概念图实质上就是将文字信息解构成了概念和概念间的关系这两种要素，并将它们按一定的規范绘制在图形中.因此，也可以将概念图的本质归纳为一种实现知识可视化的工具.知识可视化是指应用视觉表征手段将人们的个体知识表示出来，形成能够直接作用于人的感官的知识外在表现形式（显性的物理知识制品），从而促进知识的传播和创新.正是基于这一本质，概念图被开发出多种洐生功能，正在被越来越广泛地运用于多种学科领域，发挥着越来越重要的作用.

概念学习是概念图研究最早、应用最广泛的领域.实践发现在小学数学概念教学中引入概念图可以明显提升教学效果.小学数学概念学习通常包括学习概念的名称、定义、特征、内涵与外延、例证、运用等内容.概念图在其中发挥的作用可归纳为以下三个方面.

一、概念图与概念体系建构

概念图表现为清晰的层级结构，在帮助学习者理整建构概念体系上具有极大优势.从静态来看，由于概念图具有高度的抽象性和概括性，通常一张图可以同时容纳概念包含的所有要点内容.同时层级结构中除了文字，还包括位置、形状、交叉连接等象元信息，即使非常复杂的概念间关系也可以在图中表现得非常直观、一目了然.

从动态来看，学习者每学习一个新的概念，都需要思考它的内涵和外延是什么、与已学知识有什么联系、应当放在图中的什么位置、与哪些概念有关、是什么样的关系等.完成了对这些问题的思考，绘制完概念图，对该概念的有意义学习也就发生了.随着学习的逐步深入，学习者不断充实和扩展概念图，建构自己的知识体系.不论是上位学习、下位学习还是组合学习都可以在图中得到很好的体现.

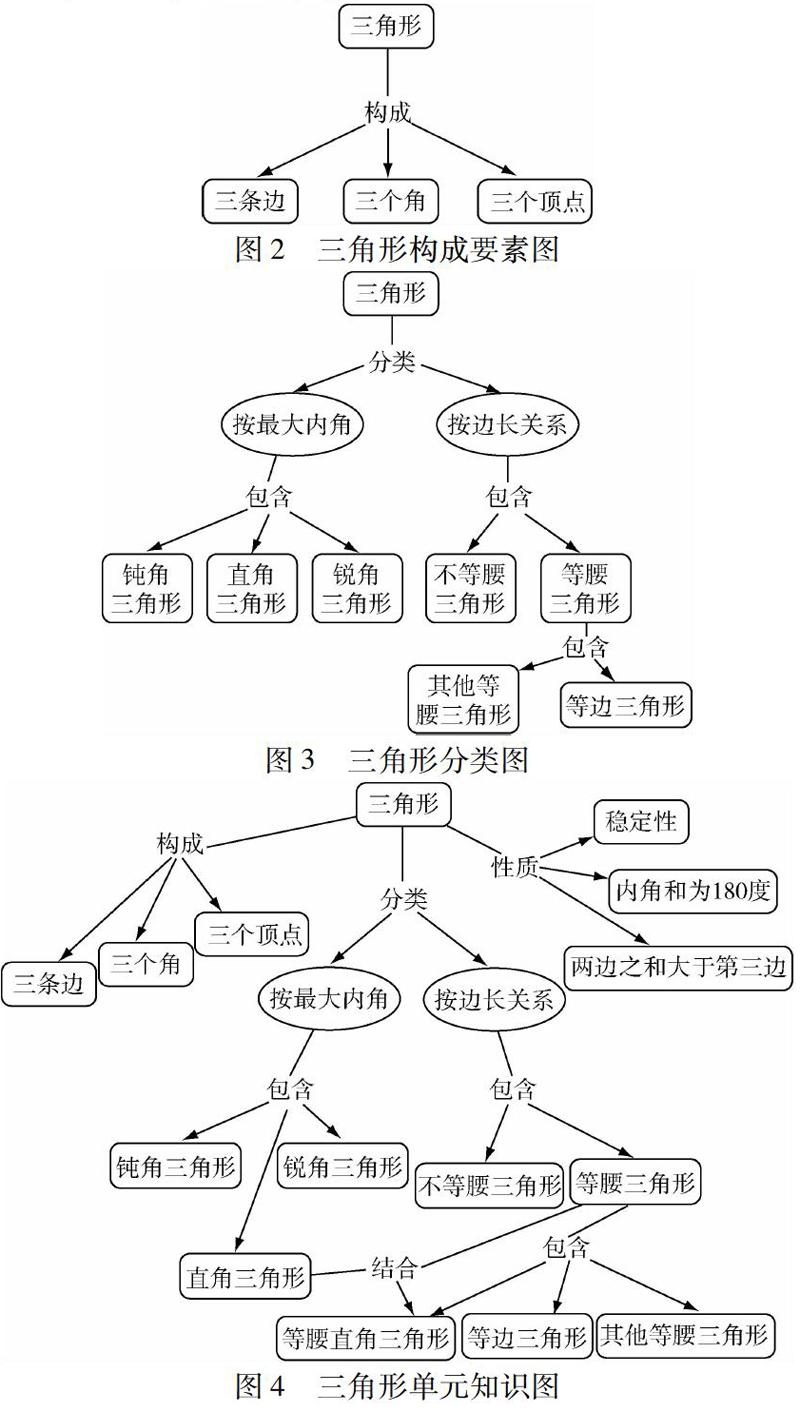
绘制概念图通常包括初建、调整、重建三种方式.仍以三角形的学习为例，刚认识三角形时可能绘制的概念图（如图2所示），图中体现了三角形的三个构成要素，这一过程就是初建.学到三角形按角如何分类时会再绘制一个概念图（如图1所示），这时并不强调它的分类标准，因此，概念间关系写的是比较简略的“包含”.继续学习了解到还可以根据边来分类时图形就可以调整为如图3所示，图中加注了分类标准.由于等边三角形是特殊的等腰三角形，因此，它在图中的位置是在等腰三角形的下一个层级.当整个单元的内容学完，就可能扩展成如图4、图2以及其他若干个小概念图都经过再调整成了其中的一部分，嵌入在了合适的层级位置上，这一过程便是重建.

可以看出不断更新的概念图成为了概念桩，将诸多原本零散的知识收纳到一个图形中，逐步建构明晰的概念体系，利于理清关系、帮助记忆、加深理解，从而提升学习效果.

二、陈述性知识向程序性知识的转化

学生学习概念时通常接触到的都是言语描述的陈述性知识.从知识学习到实践运用的转化路径通常包括：吸收陈述性知识、转化为程序性知识、执行程序、解决问题.陈述性知识是指形如“是什么”的知识;程序性知识是关于“怎么做”的知识;解决的问题包括判断一个例证是否属于这一概念等.这一路径中的关键就是如何将陈述性知识转化为程序性知识.常规教学中教师甚至学生本人都很难发现这一过程是否已经顺利完成.概念图可以很好地促成和帮助学生完成转化，教师也可借之评测学生的转化状况.

以质数与合数的学习为例，人教版教材中对两者的定义是“一个数，如果只有1和它本身两个因数，那么这样的数叫作质数（或素数）.”“一个数，如果除了1和它本身还有别的因数，那么这样的数叫作合数.”“1不是质数，也不是合数.”

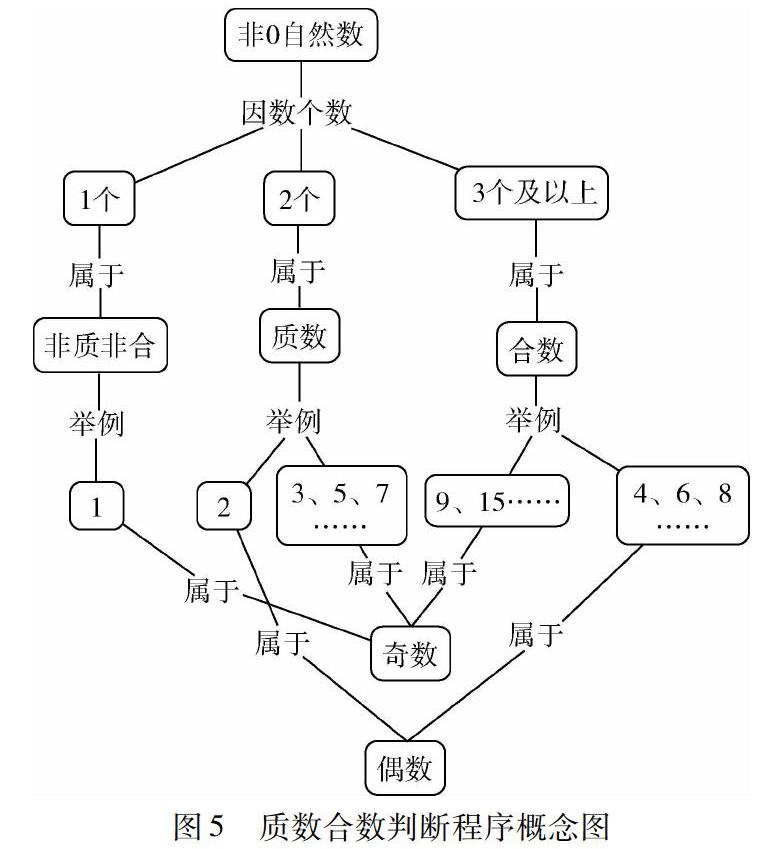
定义回答了什么是质数、什么是合数的问题，但在实际运用中往往面对的问题是如何判断一个数是质数还是合数.可以运用概念图将定义转化成如图5所示的判断程序.

从图中可以看出对质数合数的分类依据在于因数个数的不同.分类讨论是 重要的数学思想和问题解决策略，图中做了一个直观的展示.同时，还可以将之前所学的另一种数的分类——奇数和偶数融合进图中，进行对比分析与关联思考.

另外，适度抽象化的图形可以帮助学生更好地集中精力在关键信息上，引导学有余力者进行批判性思考，例如，为什么是对非0自然数进行分类？那0是质数还是合数，为什么？质数的个数是不是有限的？为什么不能把因数个数是1个和2个的统归成质数？质数与合数的个数谁多谁少？……

学习定义、性质等陈述性知识时，可以用概念图即时地转化成程序性知识，并在图中理解程序、练习程序，综合运用与解决问题时执行程序、感悟程序，以达到高效学习的目的.

三、突出本质、实现关联

概念间的联系可能直接表现为图中的交叉连接，也可能通过形状等其他信息传递出来;可能存在于同一个概念图中，也可能存在于几个相关联的概念图之间.

以长度单位的学习为例，不同的长度单位间换算具有不同的倍率.多个版本的教材中对这一内容的表达都用的是类似如下所示的公式组合.

1千米=1000米

1米=10分米

1分米=10厘米

1厘米=10毫米

这些公式在实际应用中可以衍生出如下所示更多的公式：

1千米=10000分米

1米=100厘米

1分米=100毫米

1千米=100000厘米

1米=1000毫米

1千米=1000000毫米

当然在解决诸如“23千米=（  ）厘米”这样的问题时，学生也有可能不会记忆相应的公式，而是先将其换算成“23千米=23000米”，再继续添零换算成“23千米=23000米=2300000厘米”.无论哪种方式都少不了在头脑中进行类似这样一种思维活动：将单位按顺序一字排开，思考問题中两个单位之间相差多少个间隔、这些间隔代表多少倍率，组合得出答案.

将这一思维过程可视化在概念图中就如图6所示，各单位按大小左右排列，连接线的长度不同表示不同的倍率：

看到这样的图形，很容易让人想到位数表，不同的只是将十位和百位省略了，各长度单位可以与位数表中其他位数一一对应，如图7所示：

两个知识点虽然被表示在不同的概念图中，但由于两图形状高度相似，很容易激发人们的联想.实际上两者之间确有关联，在本质上都属于进位制，只是用于表示单位的符号不同，分别是长度单位名称和数字所在的位置.同位值制中的位置一样，不同的单位名称表示长度上不同的倍率.其实汉语词典中对于分米中“分”字的解释就是“十分之一”，也就是十分位所在的倍率.同样厘、毫这两个字的释义也分别是“百分之一”和“千分之一”.它们在意思上与位数表也是对应统一的.

可以将概念图的这一类作用称之为“突出本质、实现关联”.这里的本质既可以指蕴含在不同知识点中共同的规律，也可以指它们在数学思想或方法论上的统一.教学中教师可以引导学生以概念图为突破口进行更多类似的探索和研究活动.

以上三点作用都是旨在促进学生对概念以及概念之间的联系进行更深入的关联性思考，形成更深层次的理解，促进发生更高水平的有意义学习.概念学习是整个小学数学学习的基础，可以预见引入概念图对改善小学数学教学的作用必然是巨大的.