Jump rule for edge impacts of rolling prisms
2018-02-13ZhenZhoNnnnWngCishnLiu
Zhen Zho, Nnnn Wng, Cishn Liu,*
a School of Aeronautic Science and Engineering, Beihang University, Beijing 100191, China
b State Key Laboratory for Turbulence and Complex Systems, College of Engineering, Peking University, Beijing 100871, China
Keywords:Surface impact Jump rule Experiments
A B S T R A C T We study experimentally and theoretically the planar dynamics of purely rolling prisms on a rough ramp, where the rolling motion is interrupted intermittently by edge impacts. The experiments were carried out for prisms made of different materials and having different geometries. We found that the angular velocities of the rolling prisms are material-independent, but they change significantly with their geometry. We modelled the dynamics of edge impacts by considering a socalled detachment front propagating across the contact interface. The detachment front represents the moving boundary between a detached region and a stress region that coexist within the interface plane. The theoretical analysis indicates that the detachment front can be characterized by a scale number, whose value converges to 0.4050 for prisms having large number of edges. A new jump rule for edge impacts is then developed, by which we can accurately reproduce the experimental observations, and explain why the motion of the prism is material-independent.
Understanding abrupt changes of motion of impacting bodies is critical in many scientific fields ranging from nature to engineering [1-4]. Very often, the Newton's coefficient of restitution, which is defined as the ratio of relative velocities after and before an impact, is used to monitor the state variation for two bodies impacting at a single point [5]. When impact occurs between flat surfaces of two bodies, the complex evolution of the interface stress results in anomalous post-impact responses that cannot be explained by the Newton's coefficient [5-7]. In this study we aim at developing a simple jump rule to predict accurately the post-impact responses of bodies experiencing a surface collision.
Surface impacts in a planar motion, referred to as edge impacts in this letter, can be found in many physical scenarios including a rectangular rigid block rocking on a rigid base [6, 8, 9],a prism with a polygonal cross-section rolling on a rigid ramp [5,10], and others. Currently, majority of the impact dynamic problems are mainly described via a coefficient of restitution estimated from the conservation of momentum [5, 6]. However, when this model is used in simulation, there are large discrepancies between the theoretical predictions and the experimental measurements [11, 12].
Essentially, understanding the dynamics of an edge impact requires an appropriate description of the stress field at the impacting interface [13,14]. The interface stress field during an edge-impact process evolves quickly and must result in a detachment process, which occurs through the propagation of a crack-like detachment front across the interface. The detachment front represents the moving boundary between a detached region without any contact stress and a stress region with nonzero contact stress, both of which coexist within the interface plane. We will show below that a proper description for the detachment front is crucial for developing a simple predictive jump rule of an edge impact.
In this letter, we studied experimentally and theoretically the planar dynamics of prisms undergoing a pure rotation on an inclined rough surface. In so-called pure-rotation situations, the prism rotates orderly around each vertex without detachment and slippage at the contact vertex. We found from experiments that the rolling velocity in the pure-rotation situations is material-independent, but it changes significantly with some geometric aspects. By a careful modeling of the dynamic evolution of the interface stress field, we first analyze the propagation of the detachment front, then deduce a simple jump rule for the edge impact. It is demonstrated that the intriguing experimental phenomenon is a consequence of this jump rule.
The experiments were performed on a glass plate with thickness 6 mm, width 300 mm and length 650 mm, inclined over a horizontal platform (see a schematic in Fig. 1). In order to isolate the vibration induced by the prism's motion, we inserted a 4 mm thick silica gel sheet between the glass plate and the platform. The vibration was further suppressed by paving silica gel sheets over the upper surface of the glass plate (only on the region outside the prism's rolling path). We placed the glass plate with a very small angle () to achieve the experimental objective for a prism to exhibit a pure rotation (without slippage).
The prism geometry is fully described by edge numberand radius(distance from the prism's centre to an edge corner).We designateas the central angle andthe edge width. All prisms tested in our experiments were manufactured with high machining precision, and they were galvanized for the effective reflection of laser beams. The galvanization treatment has a little influence on the physical property of the contact interface.
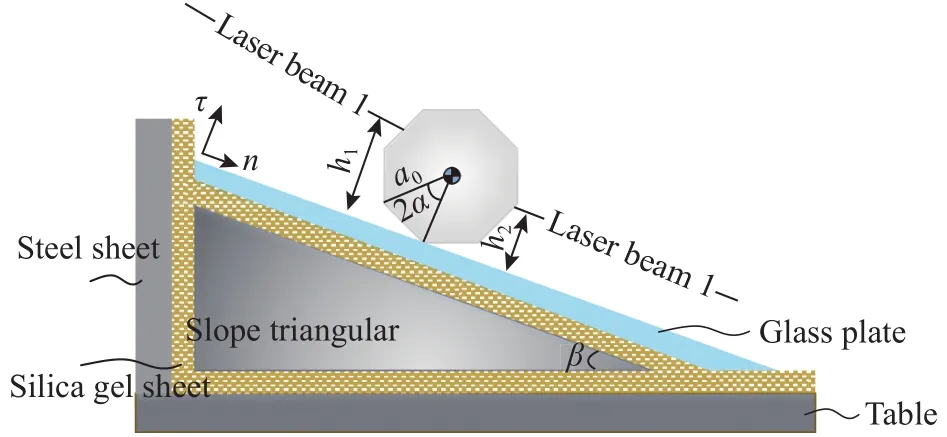
Fig. 1. A schematic of a rolling prism on a rough glass ramp. A pair of laser-Doppler vibrometers (Polytec-OFV-3001-353) emit laser beams parallel to the plate surface shooting on two sides of a rolling prism, measuring the velocities of two points intersected by two laser beams.
Tested prisms were initially tilted with a small angle on the glass plate, then released to trigger a rolling motion. Two laser-Doppler vibrometers (Polytec-OFV-3001-353) emit laser beams parallel to the plate surface shooting on two sides of a rolling prism, as shown in Fig. 1. Hence, the instantaneous velocities of the prism along the beams can be easily obtained. We have tested pure rotations of two prisms made of steel and aluminium, respectively. The two prisms have the same geometry with,mm, andmm. Figure 2 shows their angular velocities measured separately in two independent experiments. The two measured curves overlap in spite of an observable deviation in their initial stages. In terms of the experimental evidence, we conjecture that the rolling motion may be independent of the prisms' material.
The prism's geometry, however, influences the pure rotation significantly. This phenomenon was demonstrated in the experiments for six steel prisms with the same radiusmm and the same lengthmm, but with a different edge number as= 22, 24, 30, 32, 36, and 38. By defining a ratio,, as an angular coefficient of restitution, we can scale the rapid change of the angular velocity at the occurrence of an edge impact at time. From the experimental data, we extract the values of. Figure 3 shows thatis nearly constant for each prism, yet its mean value increases with edge number.
When the conservation of angular momentum about the leading corner (the corner with a maximum velocity at the start of the impact) is applied to estimate the ratio, its value can be calculated from a well known formulae [5],

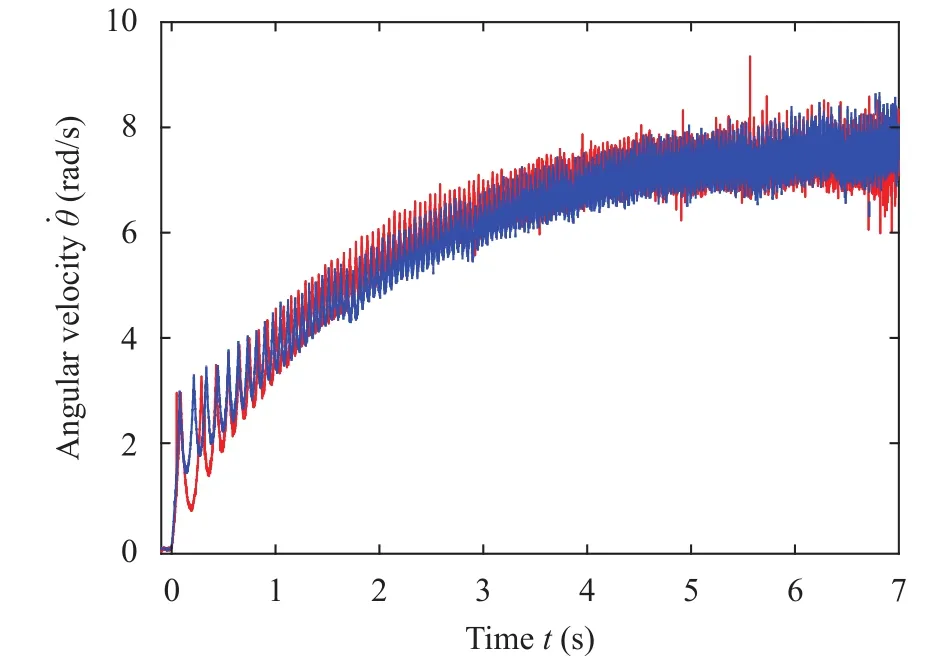
Fig. 2. Time histories of two prisms with the same geometry made of steel (red line) and aluminium (blue line) show essentially the same rolling motion.

Fig. 3. Angular coefficient of restitution,, as a function of impacts number. Stars represent the values of extracted from experimental data, and blue dash-doted lines represent the average values of, for prisms with an edge number as : .
In essence, an edge impact makes the impacting interface subject to dynamical stress, whose evolution results in a detachment front propagating across the contact interface. The detachment front is initially at the pivot corner (the rolling vertex before the impact), and then it arrives at the leading corner when the impact finishes. With regards to the propagation of the detachment front, the stress region of the contact interface decreases until the two contacting surfaces are fully separated.
We conjecture that the propagation of the detachment front consists of two phases: a slow and fast regime. The slow regime is related to the detached region on which any contact point completes a loading-uploading cycle almost without any energy dissipation. The fast regime is related to the detachment front that propagates too fast to have time to recover the remaining elastic energy, leading to an elastic hysteresis loss in the separating interface [15, 16]. The detachment front initially propagates in a slow regime until the moment when the normal velocity at the leading corner vanishes, then it starts the fast regime until the end of the impact. It is worthy noting that the prism in the pure-rotation ends each edge impact by entering into a fixed-axis rotation around a leading corner of the edge impact. This kinematics of the post-impact state of the prism is consistent with the terminal condition of the slow regime. This implies that the phase in the fast regime can be ignorable, but it plays a role of characterizing the energy dissipation in the edge impact.
Following the kinematic relationship of a rigid body, the normal velocity at the contact interface is distributed linearly at any time. We introduce a thin elastic boundary layer with thicknessbetween the surfaces of the prism and the glass plate and use a linear strain-stress relationship responsible for its mechanical behaviour. The normal stress of the interface is also distributed linearly at any time [7]. We designateandas a pivot and a leading corner, respectively. Figure 4(a) presents the temporal profiles of fields for the normal velocityand the normal stresswhen the detachment front has propagated a length. We assume that the detachment front ends its slow regime at time, and at that time, it covers a distanceand the temporal profiles ofandare plotted in Fig. 4(b). The elastic strain energy enclosed in area, whereis the edge width, corresponds to the dissipated energy through the process of the detachment front propagation in the fast regime.
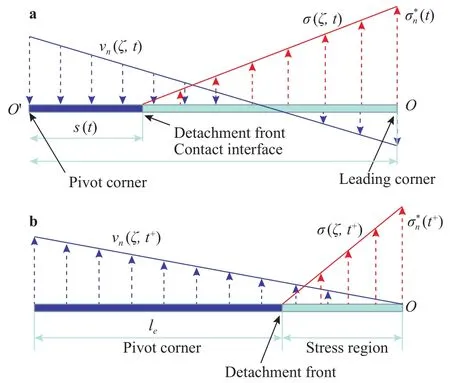
Fig. 4. Distributions of normal velocity field and normal stress field of the interface in an edge impact related to the detachment front propagating: a In the slow regime; b At the end time of the slow regime. represents the normal stress at leading corner.
From the geometric profile of the normal stress field shown in Fig. 4(a), the resultant normal force applied on the prism per unit length is given by,whereis the normal stress at the leading corner. The net momentabout the prism's center can be expressed as. The resultant friction forceis determined uniquely by the kinematic condition of the pure rotation, where no tangential velocity exists in the interface. The net friction moment induced byis obtained by. The effects from gravity and air resistance on the edge impact are completely neglected in modeling. Finally, the dynamics of the edge impact is governed by [7]
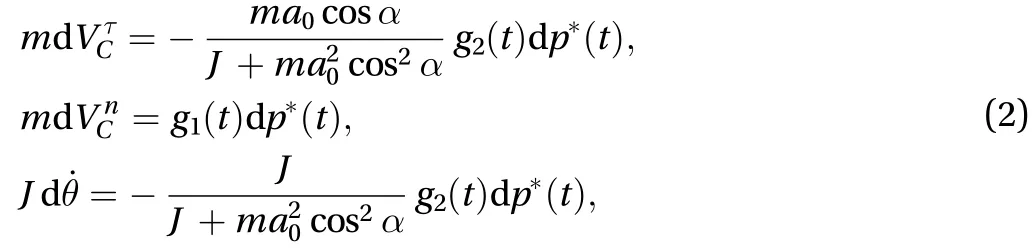
In terms of the initial and terminal conditions of an edge impact, where the prism takes a fixed-axis rotation before and after the impact, using the kinematical relationship of a rigid body, we easilyobtain,, and represents the change of kinematic quantitiesbefore and after impact. These kinematic conditions combined with the integrals of Eq. (2) enable us to establish a new jump rule:
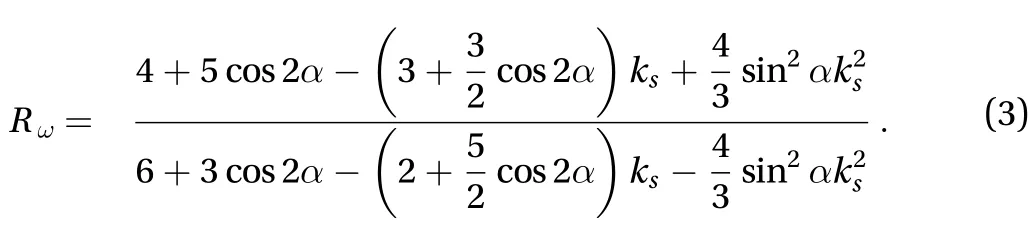
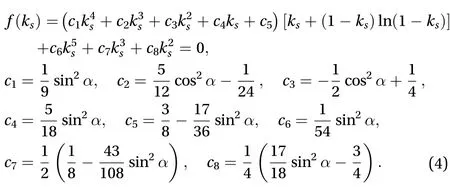
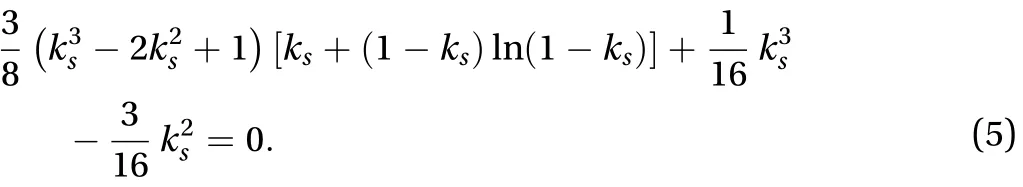
Equation (5) has a unique solution ofin the range [0, 1]. We define this constant as a scale number in association with the propagation length of the detachment front in the slow regime. Namely, at the end of the slow regime, there is a detached region with length,, on the contact interface.After that moment, the propagation of the detachment front enters into the fast regime, through which the elastic energy residing in the regionis completely dissipated.
Note that the prism moves in a fixed-axis rotation in between two neighboring edge impacts, and the rotation is governed by. This equation plus the jump rule of edge impacts enables us to simulate the whole process of the prism in a purely rolling motion. Figure 5(c) shows the evolutions of the angular velocities for prisms with, 30, and 38. Clearly, the numerical results based on the jump rule Eq. (3)accurately agree with the experimental data while those calculated from Eq. (1) differs significantly.
The difference of the jump rules between Eqs. (1) and (3) can be further exposed by an index defined as, which corresponds to the ratio between the dissipated and the initial kinetic energy of an edge impact. Let us consider a prism with a large edge number, which leads toandin approximation. The indexes obtained by Eqs.(1) and (3) arerespectively, and they are almost double the difference.

Fig. 5. a vs edge number converging 0.4050, which is the scale number. b vs obtained from Eq. (1) (blue), Eq. (3) with the value ofby Eq. (4) (red), or equal to the scale number (green). Stars represent the average values of extracted from the experiments. c Angular velocities of the prisms with edge number N = 22, 30, 38, obtained from the experiments and the numerical simulations by using different jump rules for the edge impacts.
Based on the above modeling and analysis, we can state that the intriguing phenomenon found in our experiments can be explained by the jump rule developed in this letter. When the prism purely rolls down a ramp, the dynamics of the fixed-axis rotation and the jump rule of edge impacts are only related to central angle, which is a geometrical-dependent parameter.Therefore, the pure rotation of a prism is material-independent,yet it is significantly affected by its geometry. This property,however, will be destroyed when slippage or detachment occurs in the rolling motion.
Another interesting phenomenon exhibited in the experiments is that the rolling motion gradually converges to a steady state. This state can be reached because the energy dissipation of an edge impact is compensated by the gravity potential energy released from the downwards motion of the prism [5]. Balance between them results in the steady pre-impact velocity,
In summary, we have investigated experimentally and theoretically the dynamics of the edge impact by carefully considering the propagation of a detachment front across the contact interface. By limiting the motion of the prism in a pure rotation, we found that the detachment front can be scaled to a scale number, whose value converges to 0.4050 when edge numberis large enough. A simple jump rule has been then proposed to accurately predict the angular coefficient of restitution, which represents the ratio of the angular velocities before and after an edge impact. In terms of the jump rule for the edge impacts, we can precisely reproduce the experimental phenomena, and explain why the motion of the prism in a pure rolling motion is material-independent.
Our results may have interesting ramifications beyond systems with edge impacts. A rolling prism can be considered as the system with edge impacts to imitate energy dissipation involved in the rolling motion of an elastic cylinder. Therefore, our results can be useful to elucidate the physical mechanism of energy dissipation hidden in rolling resistance, which is still a controversial issue in the field of contact mechanics [18-21].
Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 11572017).
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Data-driven computing in elasticity via kernel regression
- The effects of mean sea level rise and strengthened winds on extreme sea levels in the Baltic Sea
- New interpretation of specific sign of Reynolds stress in the boundary layer on a flat plate
- An improved smoke-wire flow visualization technique using capacitor as power source
- Head-on collision between two hydroelastic solitary waves with Plotnikov-Toland's plate model
- Linear, nonlinear dynamics, and sensitivity analysis of a vibratory ring gyroscope
