Data-driven computing in elasticity via kernel regression

Yoshihiro Kanno*

Mathematics and Informatics Center, The University of Tokyo, Tokyo 113-8656, Japan

Keywords:Data-driven computational mechanics Model-free method Nonparametric method Kernel regression Nadaraya–Watson estimator

A BSTRAC T This paper presents a simple nonparametric regression approach to data-driven computing in elasticity. We apply the kernel regression to the material data set, and formulate a system of nonlinear equations solved to obtain a static equilibrium state of an elastic structure. Preliminary numerical experiments illustrate that, compared with existing methods, the proposed method finds a reasonable solution even if data points distribute coarsely in a given material data set.

Study of data-driven solvers in computational mechanics has recently been emerging [1–11]. These solvers attempt to directly utilize a material data set, without empirical modeling of a material constitutive law on which conventional methods in computational mechanics rely. For example, for static equilibrium analysis of elastic structures, Kirchdoerfer and Ortiz [7] proposed to minimize the distance between a given material data set and the pairs of strain and stress satisfying the compatibility conditions and the force-balance equations. Independently and almost simultaneously, Ibañez et al. [4] proposed a different approach using a manifold learning technique to estimate the material behavior. To reduce high variance involved in the original one [7], Kirchdoerfer and Ortiz [8] proposed a method minimizing the weighted sum of distances with the penalty on the entropy maximization. Kanno [6] proposed to use the local robust regression to avoid influence of outliers involved in a material data set.

The method in Ref. [7] requires to solve an optimization problem possessing combinatorial properties. It is shown in Ref.[12] that the heuristic proposed in Ref. [7] does not necessarily converge to a correct solution of this optimization problem. Although a mixed-integer programming (MIP) approach in Ref.[12] is guaranteed to find an optimal solution, it is computationally expensive. The optimization problem to be solved in the method presented in Ref. [8] is a nonconvex continuous optimization problem. As illustrated in the numerical experiments in this paper, a standard nonlinear programming (NLP) approach likely often converges to an inutile local optimal solution of this optimization problem. Kirchdoerfer and Ortiz [8] proposed a simulated annealing for this problem. Since it is a metaheuristic,it does not necessarily find an optimal solution, and metaheuristics are, in general, computationally expensive.

The formulation proposed in Ref. [7] is regarded as a lazy learning method, where no model is learned from a given data set. In this short paper, we probe potentials of an alternative nonparametric method based on statistical learning. Specifically, we apply the kernel regression to static equilibrium analysis of elastic structures. The proposed method is simple, and easy to understand. It solves a system of nonlinear equations to find an equilibrium state, rather than a nonconvex optimization problem. This method differs from the one proposed in Ref. [12], in the manner that the former is based on the nonparametric regression and can deal with any static problems in elasticity while the latter uses the local linear regression and is restricted to trusses. Also, existence of solution is established for the former method, while the latter formulation does not necessarily have a solution.

For simplicity of the presentation, we consider trusses undergoing small deformation. Throughout the paper, we assume elasticity.

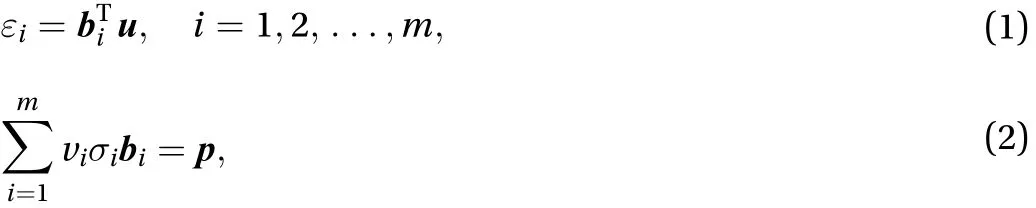
Suppose that experimental material data are given. We useto denote the given data set, whereandare observed uniaxial strain and stress values, respectively, anddis the number of observations. For eachwe estimate the stress, denotedsi, for a givenεiby using the kernel regression [13] (a.k.a. the Nadaraya–Watson estimator). We adopt the Gaussian kernel, which yields the form

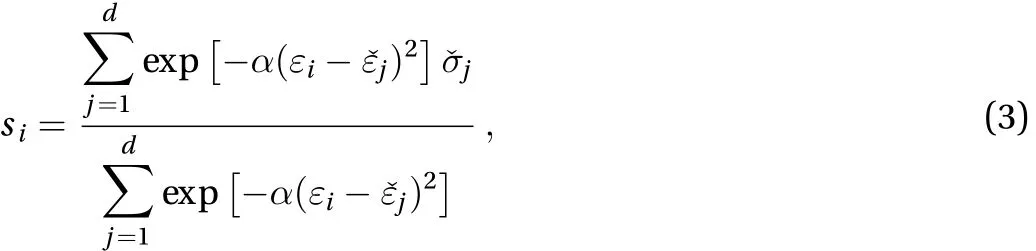
whereα＞0 is a parameter determined by the cross-validation usingD. A data-driven solver can then be formulated naturally as

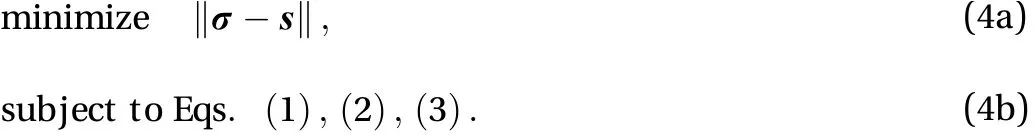
We can use a conventional NLP approach to find a local optimal solution of Eq. (4).

We may consider to use, e.g., thein Eq.(4a). A different choice of a norm leads to different feature of the solution; see, e.g., Boyd and Vandenberghe [14]. For thenorm, we can replace Eq. (4a) withAlso, we may use a loss function for robust regression, as done in Ref. [6].

We next show that Eq. (4) is reduced to a much simpler problem under a mild and mechanically reasonable assumption.Definewith Eq. (3). It is worth noting thatis continuous. Suppose that, for every, the strain energyis coercive. Then a standard verification [15] shows that the corresponding minimization problem of the total potential energy has at least one optimal solution for any. This means that the optimal value of Eq. (4) is zero.Therefore, there exists at least one solution to the following system of nonlinear equations

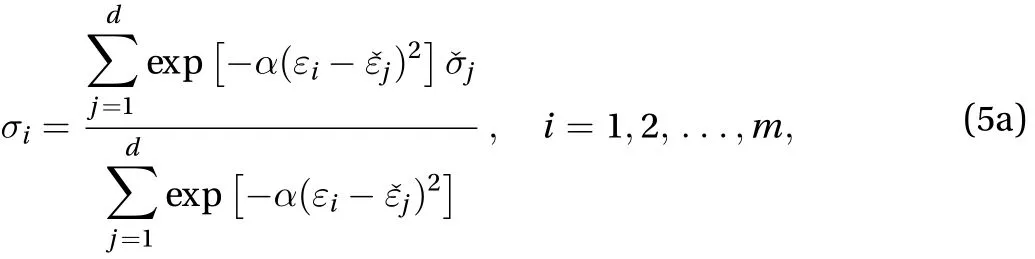
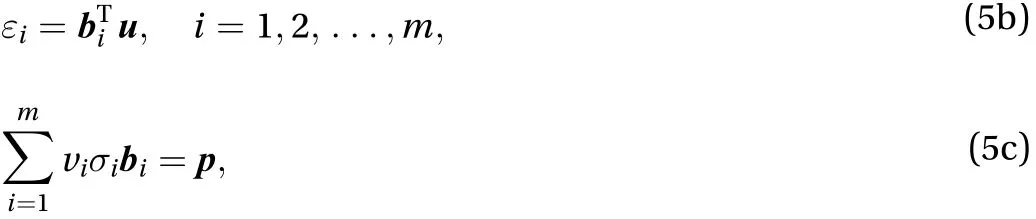
Remark1. Extension of the proposed method to a continuum discretized by the conventional finite element method is fairly straightforward. Suppose now that the material data set isare secondorder symmetric tensors with the dimension three. We replace Eq. (5a) with

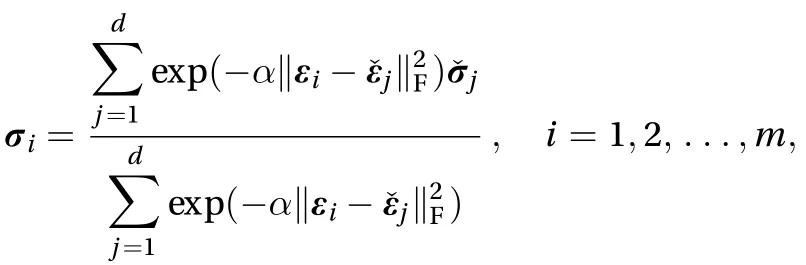
Fig. 1. 10-bar truss.

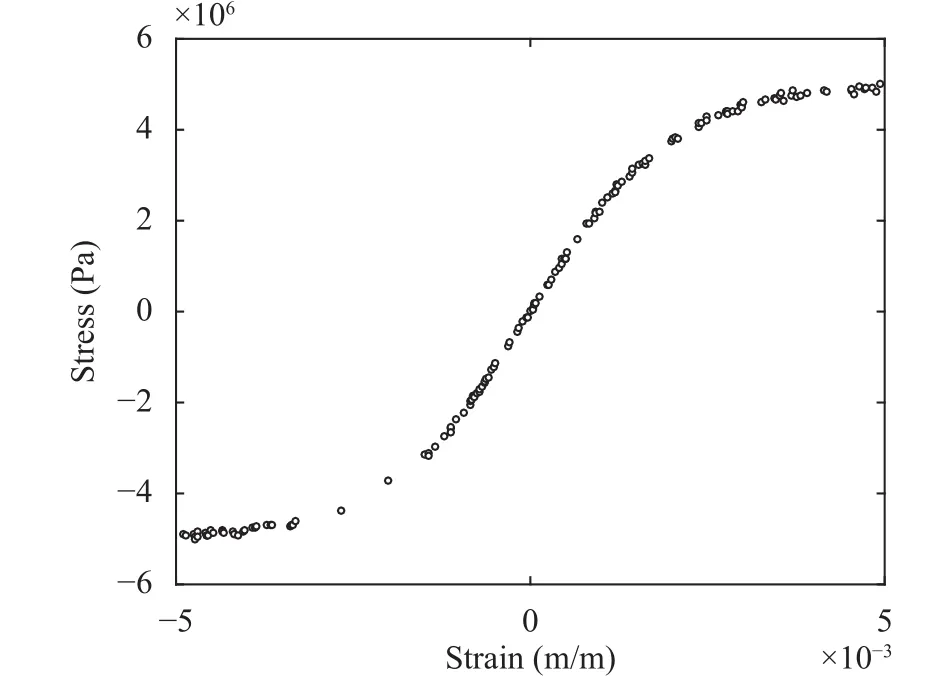
Fig. 2. Material data set for the numerical experiments.

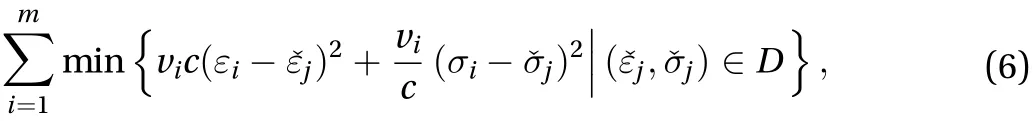
under the constraints of Eqs. (1) and (2), whereis a hyperparameter. As observed in the numerical experiments in Ref. [10], quality of the solution depends on the value ofc.

The proposed method was implemented in Matlab ver. 9.0.The system of nonlinear equations in Eq. (5) was solved by using the Matlab built-in function "fsolve" with the default setting.

Consider the truss shown in Fig. 1, whereThe cross-sectional area of each member is 2000 mm2. As for the external load, vertical forces ofkN are applied at the bottom nodes, whereis the load multiplier. Figure 2 shows a material data set consisting of 150 data points.

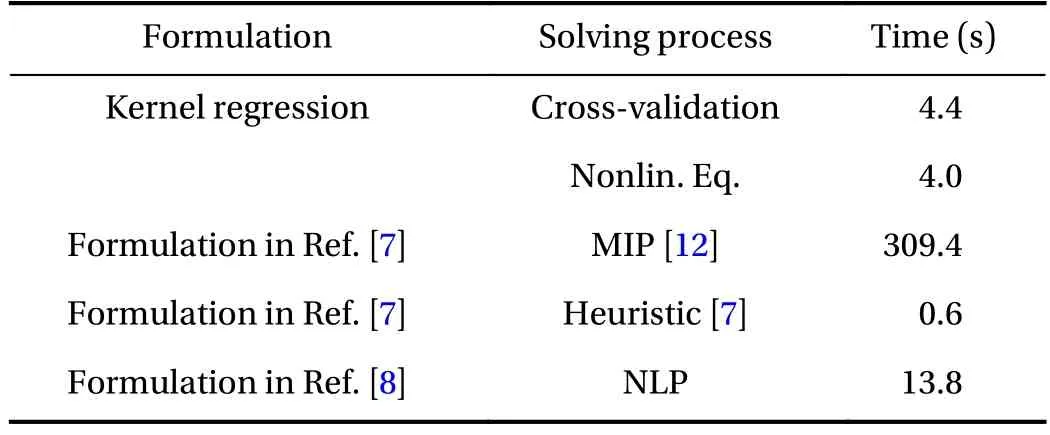
Table 1 Computational costs.

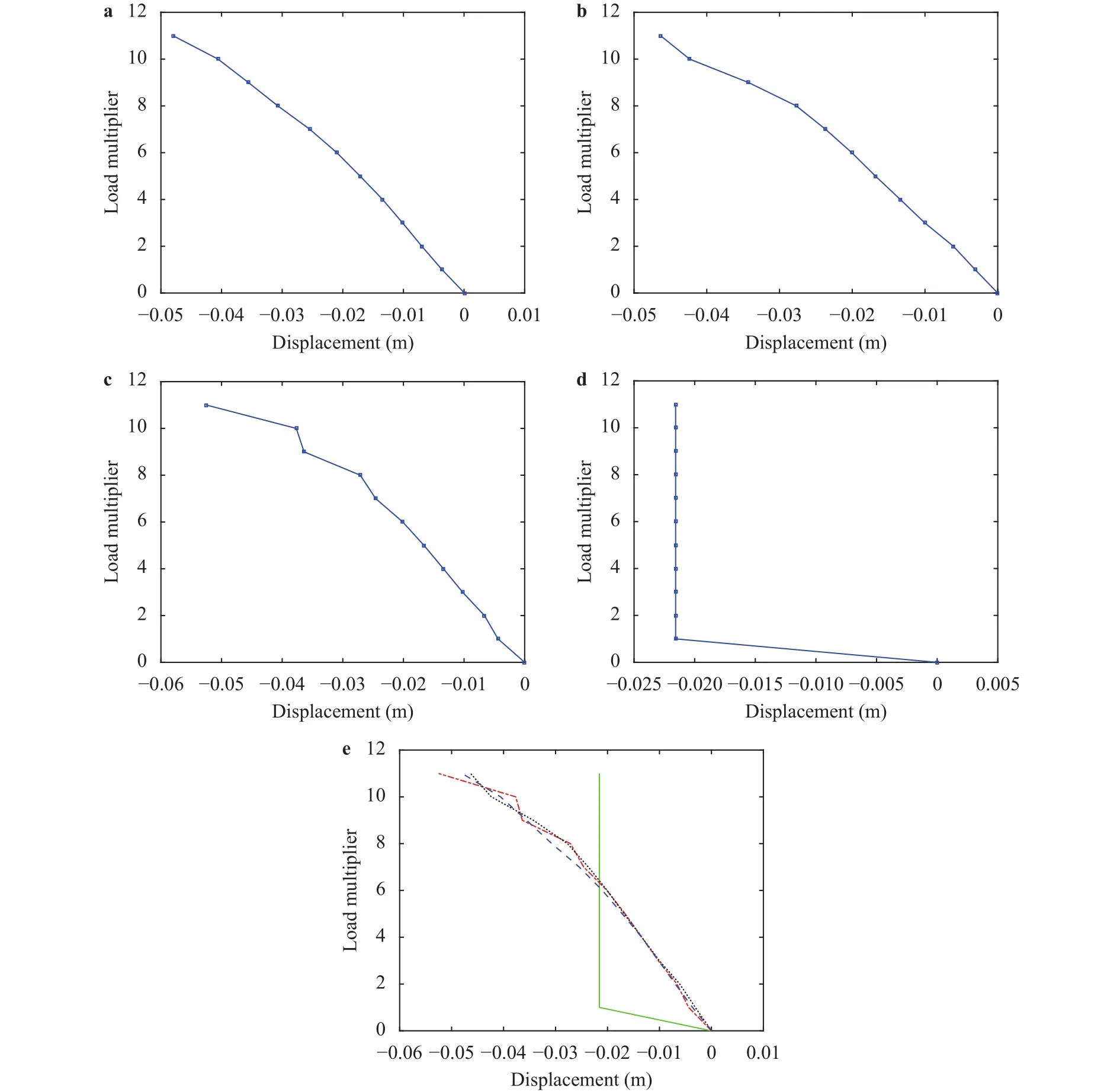
Fig. 3. Obtained equilibrium paths. (a) Solutions of the proposed method (also, dashed line in (e)). (b) Optimal solutions of the formulation in Ref. [7] (dotted line in (e)). (c) Solutions obtained by the heuristic in Ref. [7] (dashed-dotted line in (e)). (d) Solutions obtained by applying a nonlinear programming approach to the formulation in Ref. [8] (solid line in (e)).

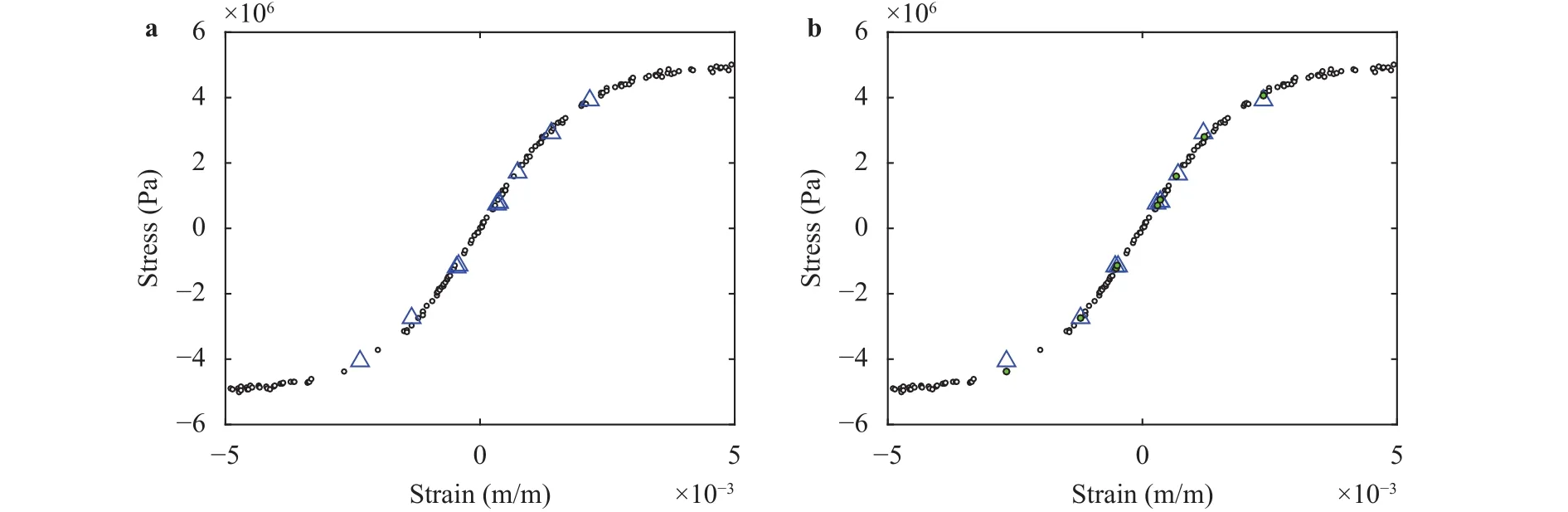
Fig. 4. Solutions obtained for. (a) Proposed method and (b) method in Ref. [12] applied to the formulation in Ref. [7]. “Circle” stands for material data point and “triangle” obtained pair of strain and stress. “F illed circle” in (b) shows the closest material data point to the obtained solution.

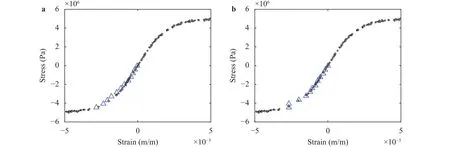
Fig. 5. Obtained strains and stresses of member (A). (a) Proposed method and (b) method in Ref. [12] applied to the formulation in Ref. [7].“Circle” stands for material data point and “Triangle” obtained pair of strain and stress.

Figure 3(a) shows the equilibrium path obtained by the proposed method, where the variation of the vertical displacement of the bottom rightmost node is depicted. The parameter of the Gaussian kernel is, which was determined by the cross-validation among candidate valuesso that the maximum error between the regression value and the data point is minimized. Table 1 reports the computational costs for the cross-validation and for solving Eq.(5), where computation was carried out on a 2.2 GHz Intel Core i5 processor with 8 GB RAM.

Figure 3(b) shows the solutions of the formulation proposed in Ref. [7]; seeRemark2. The value ofin Eq. (6) was set to the mean of. We computed global optimal solutions with the method in Ref. [12], which is computationally expensive as observed in Table 1. As an MIP solver, we used CPLEX ver. 12.8.0 [16]. Figure 3(c) shows the solutions obtained by applying the heuristic in Ref. [7] to the same formulation. This heuristic does not necessarily find optimal solutions [12]. For example, for, the objective value of the solution in Fig.3(c) is 1.316 J, while the one in Fig. 3(b) is 0.251 J. Thus, this heuristic converged an inexact solution, although it was computationally cheap.

Kirchdoerfer and Ortiz [8] proposed another formulation.Figure 3(d) shows the results obtained by applying an NLP approach to this formulation. The Matlab built-in function "fmincon" was used as an NLP solver. As commented in Ref. [8], an NLP approach often converges to meaningless local optimal solutions. This formulation involves an additional parameter,, besidesin Eq. (6). Several different values ofwere examined, but fmincon did not converge to a reasonable solution.

Figure 4 compares the solutions obtained forwhere a triangle indicates a pair of the member strain and stress,. We can observe major difference in the locations of the leftmost triangles, around which the data points distribute coarsely. Since the distance from the closest data point is minimized in the formulation in Ref. [7], the triangle in Fig. 4(b) is deviated closer to a data point, compared with the one in Fig. 4(a).We can see this difference more clearly in Fig. 5, which shows the variation ofof member (A) in Fig. 1.

In summary, we have seen that simple application of the kernel regression to computational elasticity can possibly become an effective data-driven solver. Compared with the method in Ref. [7], the proposed method provides us with a more reasonable solution when the data points distribute coarsely. Also, the proposed method is computationally inextensive compared with the methods in Refs. [7] and [8], because the proposed method solves a system of smooth nonlinear equations and the latter two methods need to solve nonconvex optimization problems globally. In contrast with the method in Ref. [6] (which is limited to skeletal structures), the method in this paper can be applied to continua.

Acknowledgments

This work is partially supported by JSPS KAKENHI (Grants 17K06633 and 18K18898).