Head-on collision between two hydroelastic solitary waves with Plotnikov-Toland's plate model

M.M. Bhatti, D.Q. Lu,*

a Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai 200072, China

b Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai 200072, China

Keywords:Head-on collision Hydroelastic solitary waves Ice sheet PLK method

A B S T R A C T Head-on collision between two hydroelastic solitary waves propagating at the surface of an incompressible and ideal fluid covered by a thin ice sheet is analytically studied by means of a singular perturbation method. The ice sheet is represented by the Plotnikov-Toland model with the help of the special Cosserat theory of hyperelastic shells and the Kirchhoff-Love plate theory,which yields the nonlinear and conservative expression for the bending forces. The shallow water assumption is taken for the fluid motion with the Boussinesq approximation. The resulting governing equations are solved asymptotically with the aid of the Poincar-Lighthill-Kuo method,and the solutions up to the third order are explicitly presented. It is observed that solitary waves after collision do not change their shapes and amplitudes. The wave profile is symmetric before collision, and it becomes, after collision, unsymmetric and titled backward in the direction of wave propagation. The wave profile significantly reduces due to greater impacts of elastic plate and surface tension. A graphical comparison is presented with published results, and the graphical comparison between linear and nonlinear elastic plate models is also shown as a special case of our study.

1 Introduction

Collision of waves is one of the major topics in marine engineering and oceanography. Scott Russell described, in 1834, the solitary waves while Korteweg and de Vries (KdV) modelled in 1895 the solitary wave mathematically in terms of the KdV equation. Gardner et al. [1] described the engrossing behavior of collision between solitary waves by means of the inverse scattering transform (IST) method, and found that during the collision process, the solitary waves exchange their positions and energies with each other and regain their original forms after separation.According to the IST method [1], all the KdV solitary waves propagate along the similar direction. However, for a head-on collision between a pair of solitary waves, an efficient asymptotic expansion can be used to simulate the original field equations.F or this purpose, the Poincar-Lighthill-Kuo (PLK) method [2-5],which in essence involves the method of strained co-ordinates,has been introduced to determine the head-on collision between solitary waves. For the head-on collision between two solitary waves, Maxworthy [6] found experimentally that the waves achieve their maximum amplitude which is twice times greater than the initial wave amplitude and during interaction they cause a time delay. Dai [7] described the interaction between solitary waves in a two-layer fluid under the effect of surface tension. He examined that the two critical cases in which the impact of nonlinearity and dispersion can not balance each other under the consideration of original approximation. Mirie and Su [8] analyzed the head-on collision between two modified KdV solitary waves in which the cubic nonlinearities and quadratic nonlinearities balance dispersion. Dai et al. [9] found the fourth order series solution for the head-on collision of solitary waves in an incompressible Mooney-Rivlin elastic rod. Cohen and Dai [10] investigated the nonlinear axisymmetric long amplitude waves in a compressible hydroelastic rod. Recently, Ozden and Demiray [11] applied the extended PLK method to analyze the head-on collision between a pair of solitary waves, and they provided a comparison between the PLK method and the extended PLK method and found that the mathematical results with both methodologies are the same.

The interaction of solitary waves in a non-integrable system is inelastic and after colliding solitary waves exchange energies.Solitary waves are found in various fields such as fluids, plasma,and liquid crystal etc. In shallow water, internal solitary waves are of finite amplitude, non-sinusoidal that propagate in stratified fluids along density interfaces. In different cases the amplitude of the solitary waves can be compared with the depth of water i.e., the presence of seabed boundary can play a significant role in the development and wave behavior. Hsieh et al. [12]investigated numerically the behavior of internal solitary waves propagating over a submerged ridge. Agafontsev et al. [13] analyzed the internal solitary waves in deep water near the critical density ratio. They studied both the cases of internal solitary waves, supercritical bifurcations and subcritical bifurcations with the help of the nonlinear Schrdinger equation.

During the past few years, nonlinear hydroelastic problems achieved a great attention due to their numerous applications in engineering, biological and physical sciences which deals with the deformable bodies and moving fluids. Flexural-gravity waves(hydroelastic waves) occur in polar areas where the water is frozen and then it is treated as roads and aircraft runways. A number of researchers examined numerically and analytically two-dimensional nonlinear hydroelastic models beneath an ice sheet that mainly comprises on the Kirchoff-Love plate theory.Different linear and nonlinear models are very much helpful in analyzing the wave interaction with large and small floating structures, such as airports and large ships [14-18]. Korobkin and Khabakhpasheva [19] studied the influence of unsteady nonlinear hydroelastic waves onto elastic plates. Davys et al. [20]analyzed the waves originated by a concentrated point source and found the different patterns of wave crest with the help of different asymptotic Fourier techniques. Sahoo et al. [21] studied the scattering of surface waves with different geometrical aspects and edge conditions. They found that hydrodynamic behavior mainly depends on the wave conditions, geometrical configurations, and edge conditions.

The hydroelastic behavior of ice sheets is investigated experimentally and theoretically by different researchers. Părău and Vanden-Broeck [22] studied the nonlinear three-dimensional waves with a steadily moving pressure beneath an ice sheet by means of the boundary integral method. Recently, Plotnikov and Toland [23] presented the theoretical and mathematical modeling of a thin elastic sheet floating on an infinite ocean with the help of the special Cossert theory of hyperelastic shells for nonlinear hydroelastic waves which satisfy the irrotational flow theory and Kirchoff's law. Milewski et al. [24] numerically and asymptotically studied the nonlinear hydroelastic waves in deep water bounded by an elastic sheet. Wang and Lu [25] found the analytic results of nonlinear hydroelastic waves traveling in a fluid under a thin elastic plate. Recently, Bhatti and Lu [26] discussed the head-on collision between hydroelastic solitary waves with the help of the PLK method. They used a linear mathematical model for a thin elastic plate in the presence of compressive force and obtained the third-order KdV equation for the hydroelastic solitary waves.

With the above discussion mind, the purpose of this paper is to examine the head-on collision between nonlinear hydroelastic solitary waves traveling in a fluid covered by a thin ice sheet.The new model recently developed by Plotnikov and Toland [23]will be used for the ice sheet. For a general case, the surface tension of fluid is also included, which is a totally new model, to the authors' best knowledge, for the fluid-ice interaction. We consider that both the solitary waves are small in amplitudehaving long wavelength, where,andare the wave amplitude, the water depth and the wave length,respectively. Furthermore we assume that Ursell's number is about 1, namely. The solutions of the governing nonlinear equation have been obtained with the help of the PLK method up to third order approximation in Sect. 3. The PLK method is very helpful for the investigation on a collision between the solitary waves [27]. The behavior of all the physical parameters of interest is discussed and demonstrated graphically in Sect. 5 and Sect. 6. In this letter, the problem is formulated and the method of solution is presented. The detailed coefficients of the asymptotic expansions can be found in Ref. [28].

This article is contributed in memory of Prof. Yung-Huai Kuo(4 April 1909 - 5 December 1968).

2 Mathematical formulation

We consider hydroelastic waves in a channel of finite depth.Cartesian coordinate system is chosen in such a way that theaxis is taken along horizontal direction, while the-axis along the vertical direction. The horizontal plane bottom is located atwhere the normal velocity is zero since no fluid particles penetrate the bottom. The deflection of the ice plate (namely the hydroelastic wave profile) is presented atwhereis the time. The velocity field for the governing flow is described as a potential functionwithforand.

The kinematic boundary condition for the governing flow at the fluid-ice interface () can be written as

while the dynamic boundary condition reads

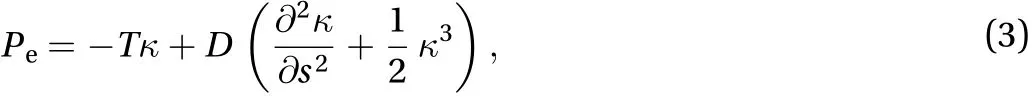
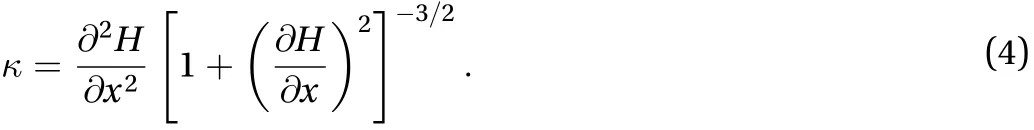
According to Guyenne and Părău [29], we have

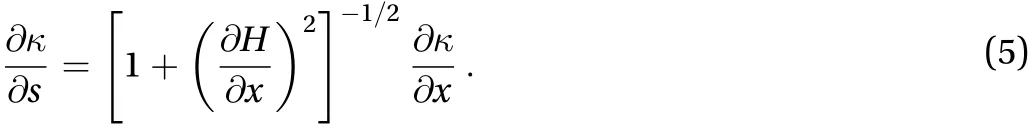
Equation (3) includes the combined effects of the surface tension of the fluid and the elasticity of the ice sheet. The second term in Eq. (3) represents Plotnikov and Toland's model, of which the linear part is the well-known linear Euler-Bernoulli beam or Kirchoff-Love plate model.

For long waves in shallow water, we can easily describe the potential functionas the Taylor series at. With the help of, we get

3 Method of solution

The solution of Eqs. (8) and (9) are found with the help of a singular perturbation method. For this purpose, in wave frame of reference we introduce the following coordinate transformations

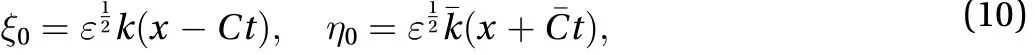
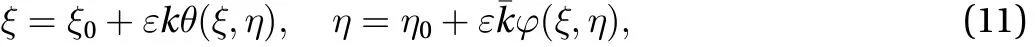
Let

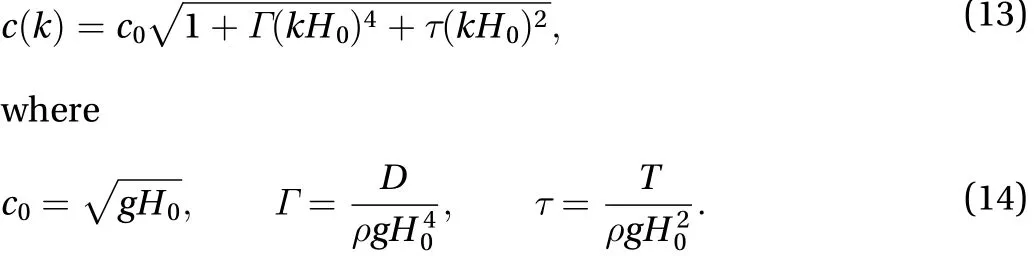
To make it more convenient, let us introduce a column vectorwhich is defined as

According to the PLK method, we expand the variables in the form of following power series

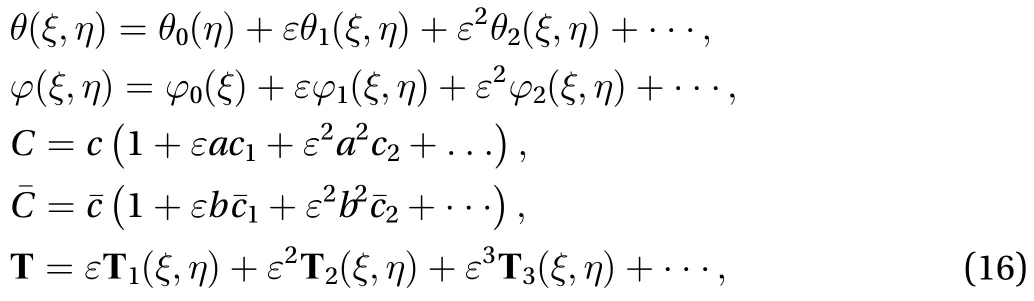
4 Perturbation Analysis

4.1 Coefficients of

The system of first-order equations reduces into the following form as

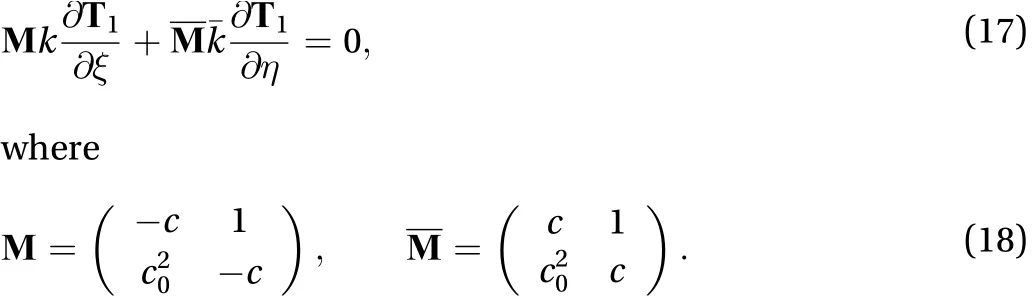
The resulting equations are highly coupled, and it is difficult to solve the equations. We introduce a matrix system for the coupled equations to obtain the solutions at each order. Su and Mirie [27] used a transformation system instead of a matrix sys-tem to get the solution. The transformation, however, is not suitable for hydroelastic wave speed (see Eq. (13)). Later, different authors [9, 30] used a matrix system to obtain the solution for pure gravity waves in single and two-layer fluid systems.

The right and left characteristic vectors ofandare

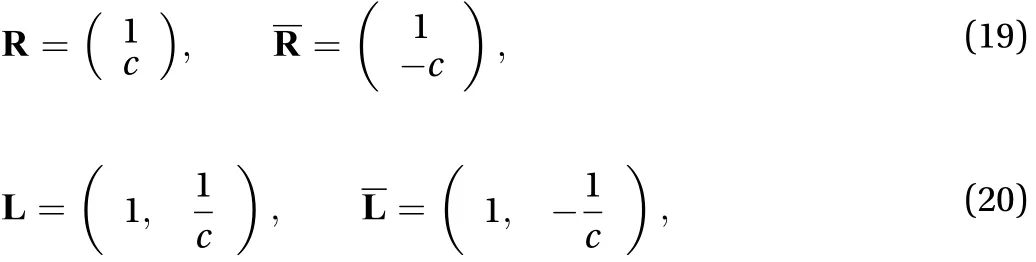
respectively. The right and left characteristic vectors in Eqs. (19)and (20) are presented to analyze the solution at each order. The left characteristic vectors help to make this coupled equations into a single equation. However, the right characteristic vector helps to approximate the solution at each order.

Let us consider the solution of Eq. (17) in the following form

4.2 Coefficients of

The system of second-order equations reduces into the following form as

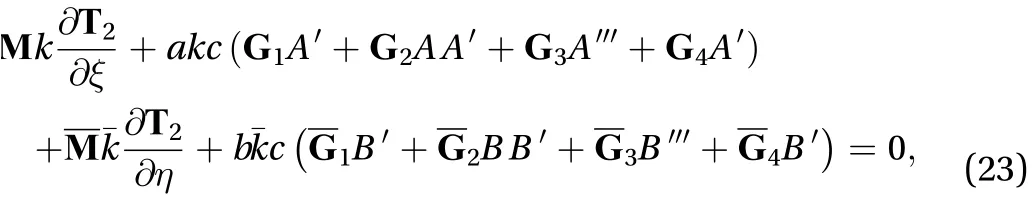
Let us assume the general solution of the following form

Using Eq. (24) in Eq. (23), and multiplying it by, we get

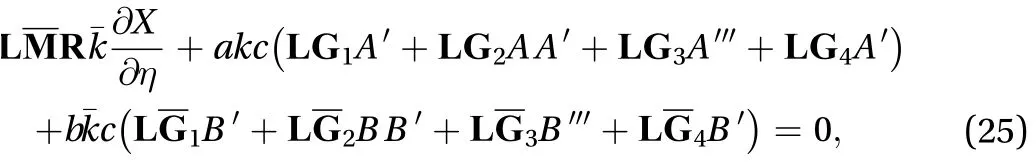
The above equation is further divided into three parts,namely (1) secular terms, (2) local terms, and (3) non-local terms.

1. Secular terms

Secular terms in Eq. (25) are those terms which do not depend on. In this equation, three terms appear that do not depend upon. The other terms cannot be treated as secular terms, because if we integrate these terms with respect to, then these terms become unbounded in space and time and show a secular behavior. These terms are

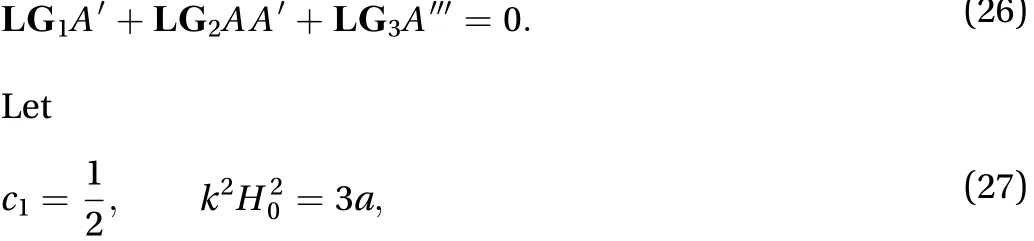
then Eq. (26) reduces to the following form

The solution of the above KdV equation can be written as

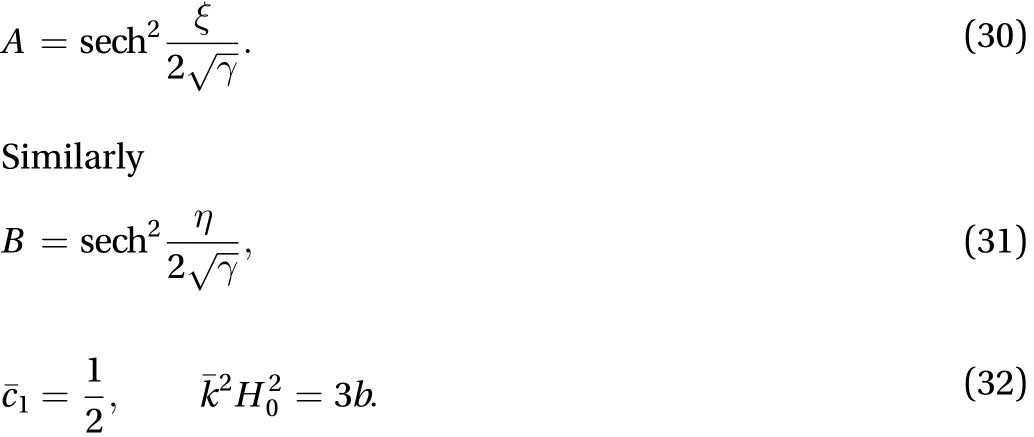
2. Non-local terms

The terms appearing in non-local terms are not secular.However, these terms are helpful to determine the phase shifts.Therefore, we will leave these terms as they are. The non-local terms in Eq. (25) are found as

The first-order phase shift reduces for the pure gravity waves astends to 1.

3. Local terms

The local terms are those terms which are helpful to examine the wave speed for the left- and right-going solitary waves.The local terms in Eq. (25) can be written in the following form as

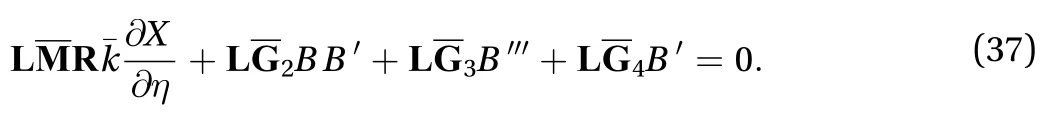
Integrating the above equation with respect towe get the resulting equation after simplification

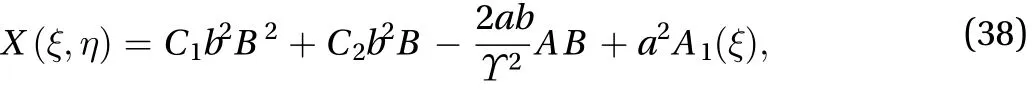
where22 hereinafter) are presented in Appendix B of Ref. [28].

Similarly we can obtain

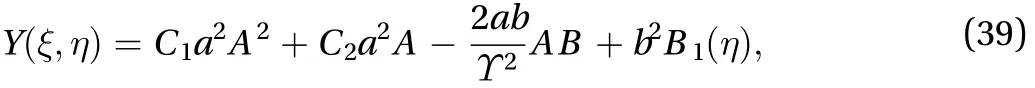
4.3 Coefficients of

The third-order system of equations can be obtained in the following form

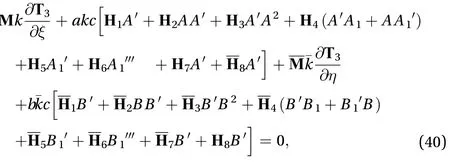
Let us assume the general solution of the following form

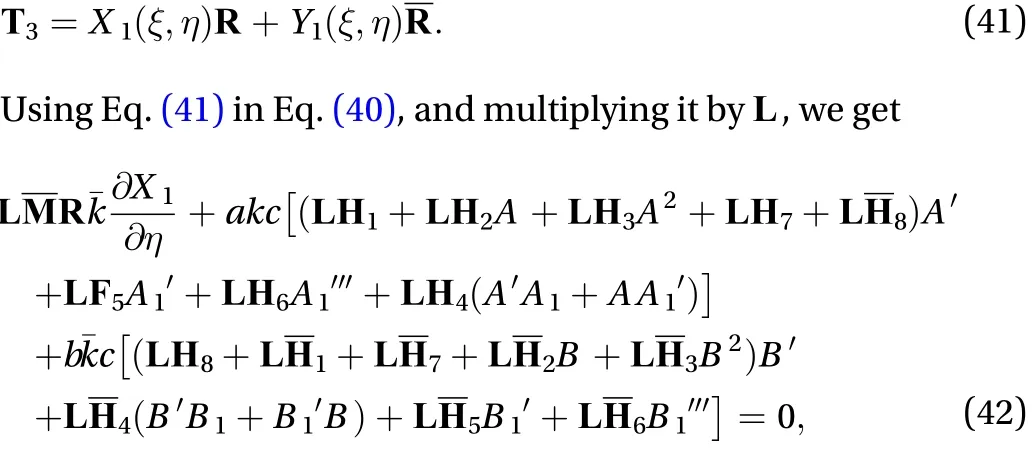
The above equation is further divided into three parts,namely (1) secular terms, (2) local terms, and (3) non-local terms.

1. Secular terms

The secular terms appearing in this order are found as

The above equation is simplified as

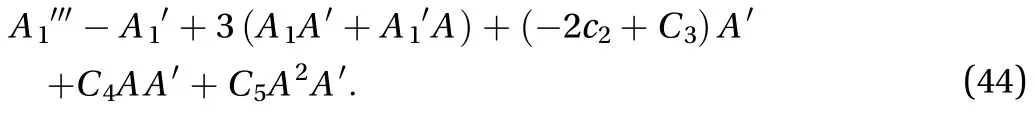
Upon integrating the above equation we get

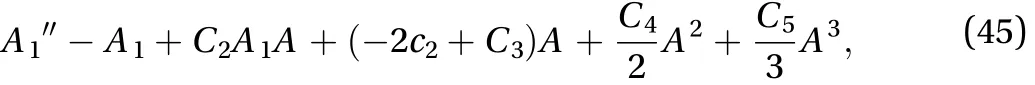
Let

then the solution of Eq. (44) can be written as

This completes the solutions for Eqs. (38) and (39).

2. Non-local terms

The non-local terms appearing in this order are found as

In Eq. (51) all the terms are similar to the first-order phase shift and show a simple phase shift behavior except the third term in. The third term independs onwhen.Therefore the wave profile is different before and after collision process (see Fig. 9), becausemoves in to the argument of function. Similar behavior has been observed for the leftgoing wave.

3. Local terms

The local terms are found as

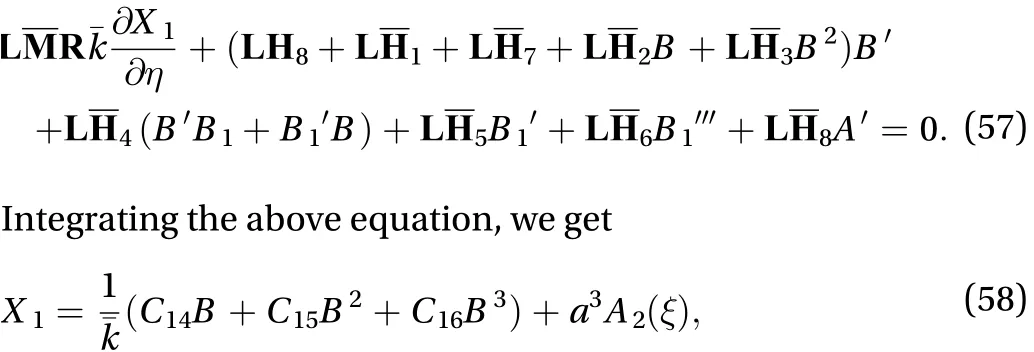
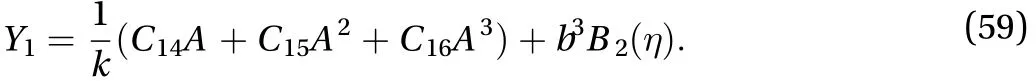
5 Analytical solutions of the problem

The series solutions in the preceding section are summarized in the following form.

The surface elevation at the fluid-plate interface can be obtained with the help of Eqs. (21) and (24) as follows

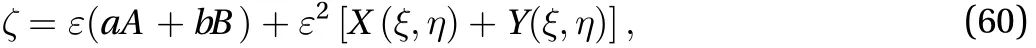
The distortion profile can be calculated with the help of Eq.(60). For this purpose the terms which are products ofandin Eq. (60) must vanish. Therefore the distortion profile at the fluid-plate interface can be obtained. After setting,we get

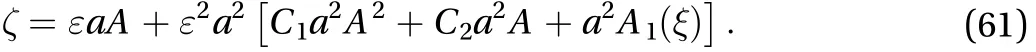
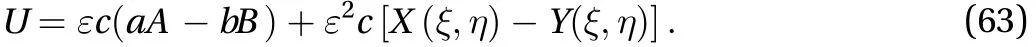
Following from Eqs. (27) and (45), the asymptotic solutions for the wave speeds read

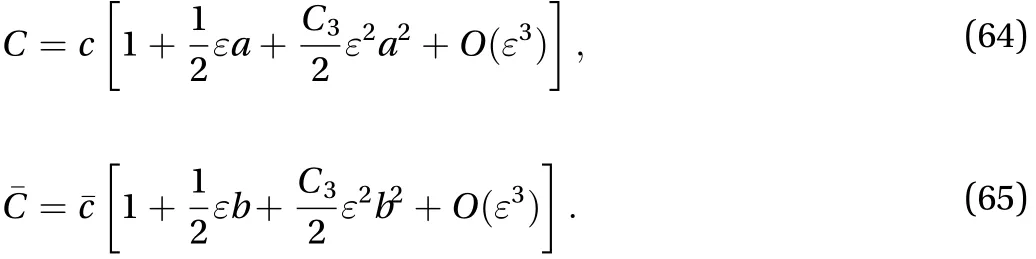
The phase shifts during the collision process read

6 Graphical results and discussion

We describe the graphical results for all the pertinent parameters involved in this hydroelastic wave problem. For this purpose Figs. 1-11 have been sketched against all the parameters.Particularly, we discuss the behavior of the fluid-plate interfacial elevation, distortion profile, maximum run-up during a collision,phase shift, and wave speed. We have considered the physical parameters i.e.for the graphical results.

Figure 1 shows the graphical comparison between linear and nonlinear models for a thin elastic plate. We can see from this figure that the behavior of both models at small amplitudes are the same and the effects are almost negligible. However, the nonlinear profile different significantly from the linear one at large amplitudes which are physically unrealistic because the ice sheet experience a higher rate of strains than it can sustain.Figure 2 is plotted for multiple values ofin Eq. (14). In this figure, we observe that the significant enhancement in the flexural rigidity parameter, providing a significant resistance which tends to diminish the interfacial surface elevation. Physically,when Young's modulusrises, the deflection of a plate becomes stiffer, and a very high rate of reactive force occurs to op-pose the deformation of an elastic plate. It depicts in Fig. 3 an increment in the surface tension parameter(see Eq. (14)) significantly reduces the amplitude of wave profile. Figure 4 shows the graphical comparison with previously published results for pure gravity waves [27] by takingand. It can be noticed from this figure that the present results are in excellent agreement.

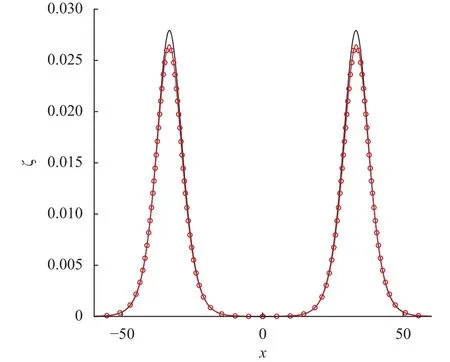
Fig. 1. Graphical comparison between linear (Kirchhoff-Love plate)model and nonlinear (Plotnikov and Toland's) model. Solid line:nonlinear model. Circle: linear model.

Fig. 2. Head-on collision between two solitary waves for different values of. Solid line:, dashed line:, dot-dashed line:, dot-dot-dashed line:.

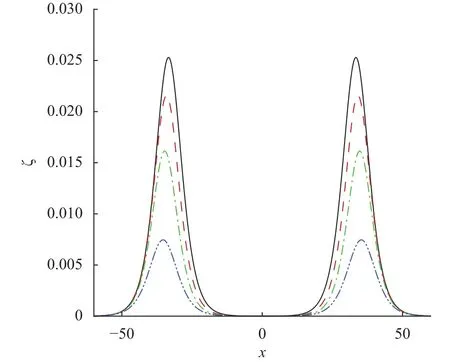
Fig. 3. Head-on collision between two solitary waves for different values of. Solid line:, dashed line:, dot-dashed line:, dot-dot-dashed line:.

Fig. 4. Comparison of head-on collision process with previous results. Solid line: Su and Mirie [27], circle line: present results, dashed line:.

Figures 5 and 6 represent the maximum run-up versus the wave amplitude during a collision process. The maximum runup during the collision process is obtained by takingin Eq. (60), and the maximum run-up amplitude exists at the pointsand. Wave run-up is a substantial phenomenon in promoting and causing the bluff erosion. It depicts in Fig. 5 thattends to diminish the maximum run-up as the wave amplitude rises. The behavior remains similar due to the surface tension effects as shown in Fig. 6. Figures 7 and 8 are sketched for the phase shift against different values ofand. Figure 7 reveals that greater impact of elastic plateand surface tensionsignificantly decline the phase shift profile.

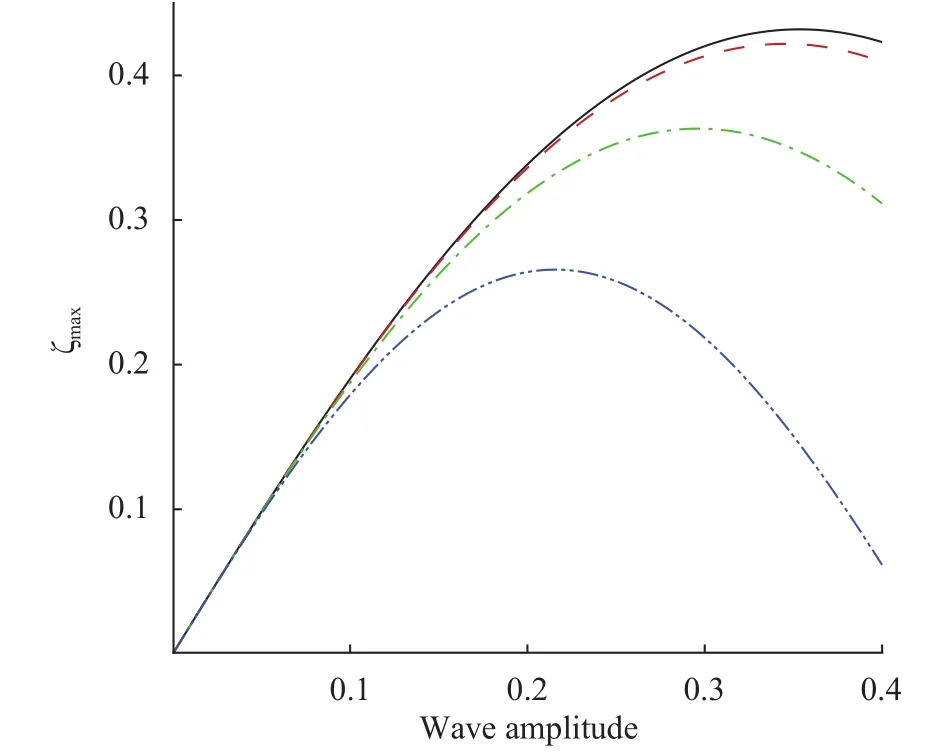
Fig. 5. Maximum run-up wave amplitude. Solid line:,dashed line:, dot-dashed line:, dot-dot-dashed line:.

Fig. 6. Maximum run-up wave amplitude. Solid line:,dashed line:, dot-dashed line:, dot-dot-dashed line:.

Figure 9 represents the distortion in the wave profile which is plotted with the help of Eq. (61). Before collision when, the wave profile is symmetric, however after the collision process, the wave profile is not symmetric and tilts backward in the direction of propagation.

Figures 10 and 11 are plotted to see the behavior of the wave speed versus the wave amplitude. In these figures, we can see that the wave speed rises as the wave amplitude increases, but when the wave amplitude increases fromthen there is a decline in the wave speed. Moreover, all the parameters, i.e.,and, cause an increasement in the wave speed when these parameters increase.

The present study reveals many interesting behaviors and provides a rich arena to study further on the head-on collision between hydroelastic solitary waves. It is also worth mentioning here that by takingandin Eq. (3) then the present results reduce to those obtained by Su and Mirie [27] for pure gravity waves.

7 Conclusions

We have formulated the head-on collision of two nonlinear hydroelastic solitary waves in a fluid covered by an ice sheet, taking the presence of surface tension effects into account. The ice sheet is considered as a thin elastic plate which is modeled with the help of the special Cossert theory of hyperelastic shells and the Kirchoff-Love plate theory. Firstly, the governing partial differential equations are transformed into wave frame coordinates in terms of phase functions for the small parameter. Then we obtained a set of differential equations. The highly nonlinear partial differential equations are solved with the help of PLK technique of strained coordiniates. The series solution up to third order has been obtained. The impact of all the parameters is discussed mathematically and graphically. In particular, we have elucidated the effects of the flexural rigidity and the surface tension on the plate-water interfacial elevation, the velocity at the bottom, phase shift, wave speed, distortion profile, and maximum run-up amplitude during a collision process.

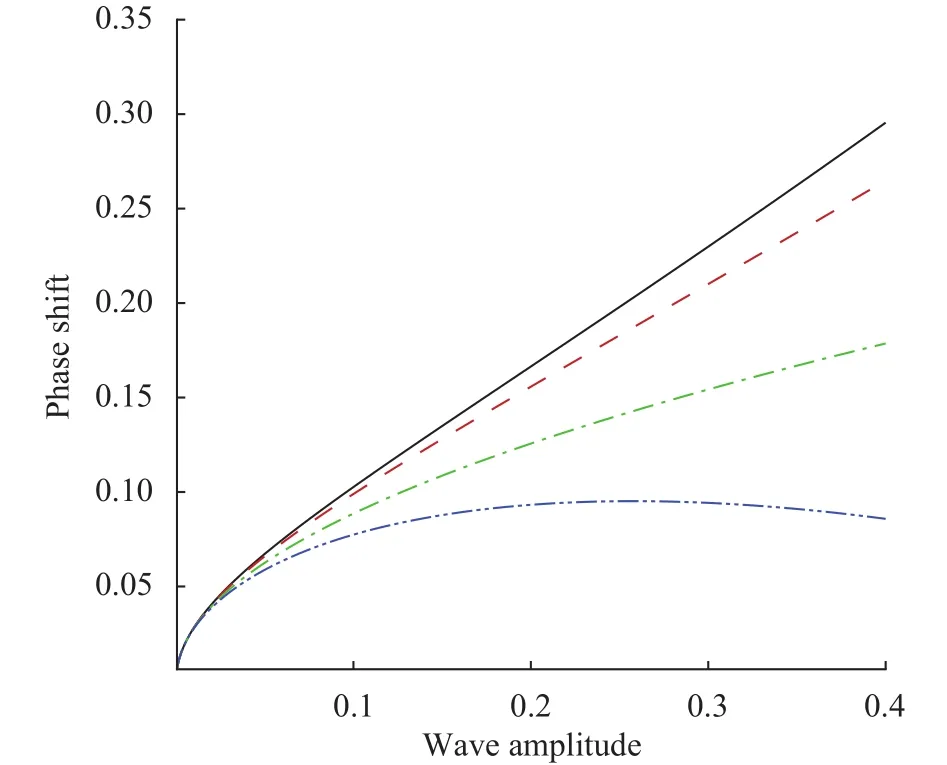
Fig. 7. Phase shift wave amplitude. Solid line:, dashed line:, dot-dashed line:, dot-dot-dashed line:.

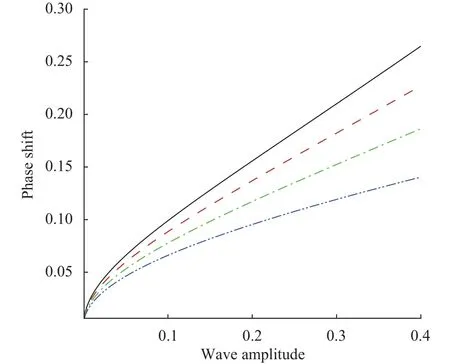
Fig. 8. Phase shift wave amplitude. Solid line:, dashed line:, dot-dashed line:, dot-dot-dashed line:.

A graphical comparison between linear and nonlinear models has been presented, and it is observed that the effects between both models are negligible at a smaller amplitude of solitary waves. Moreover, due to the plate elasticity and the fluid surface tension effects, the magnitude of the solitary wave profile tends to diminish. The wave profile tilts backward after the collision process. However, surface tension effects do not cause a significant impact during the distortion of the wave profile.Maximum run-up amplitude has also been calculated and explained with the help of graphical demonstration. The run-up amplitude decreases due to the surface tension and while its behavior is similar due to plate thickness and Young's modulus.

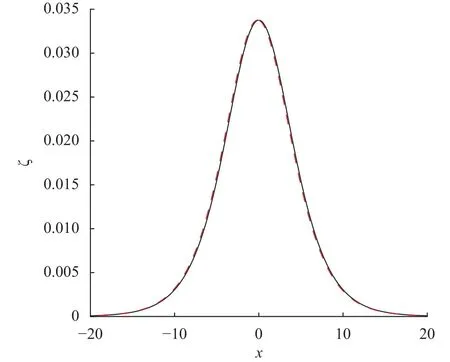
Fig. 9. Distortion profile. Solid line: before collision, dashed line:after collision.

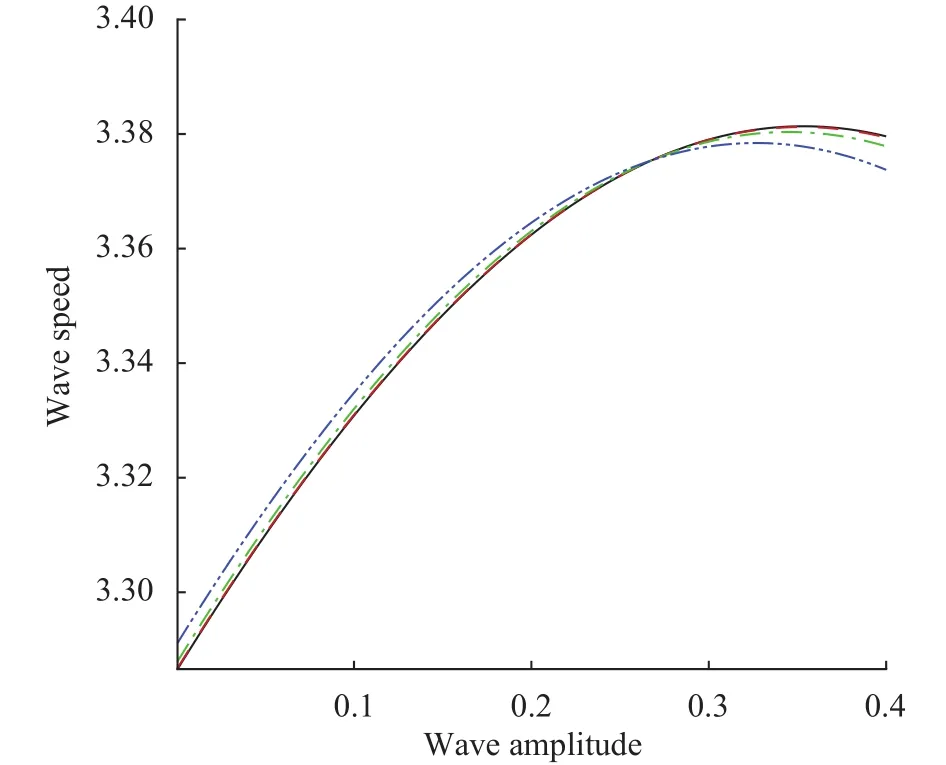
Fig. 10. Wave speed wave amplitude. Solid line:, Dashed line:, dot-dashed line:, dot-dot-dashed line:.

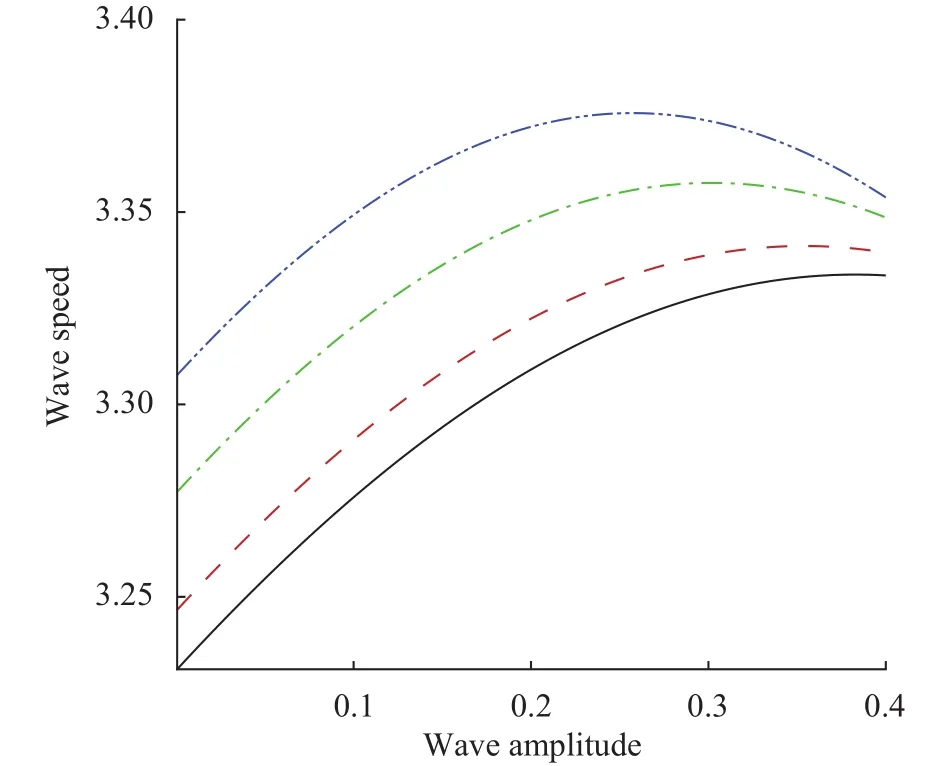
Fig. 11. Wave speed wave amplitude. Solid line:, Dashed line:, dot-dashed line:, dot-dot-dashed line:.

Further, the phase shift tends to diminish significantly due to the plate elasticity and the surface tension effects. It is found that the wave speed tends to increase due to a remarkable increment in surface tension. In the absence of the thin elastic plate and the surface tension, the present results reduce to those obtained by Su and Mirie [27] which validates that the current methodology and the obtained results are correct.

Acknowledgments

This research was sponsored by the National Natural Science Foundation of China (No. 11472166).