New interpretation of specific sign of Reynolds stress in the boundary layer on a flat plate

L.M. Lin*, Y.X. Wub

a Key Laboratory for Mechanics in Fluid Solid Coupling Systems, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190,China

b School of Engineering Sciences, University of Chinese Academy of Sciences, Beijing 100049, China

Keywords:Reynolds shear stress Sign Boundary layer Flat plate Turbulence

A BSTRAC T The specific sign of Reynolds stress in the boundary layer on a flat plate at zero incidence is newly interpreted in present paper based on the theory of vortex-induced vortex. It avoids some problems appeared in a traditional explanation, on the basis of relationship between mean and fluctuating flows due to the transport of momentum. Through the analysis of local flow field in the immediate neighborhood of wall, the characteristics of Reynolds stress are identified through introducing turbulence-induced small-scale streamwise eddies above the flat plate. The positive Reynolds stress is theoretically verified. And such new interpretation illustrates that the generation of Reynolds stress, as well as fluctuating velocity, is intrinsically independent of the mean flow. But its specific sign would be determined by the mean flow due to the inertial forces. Other features,such as the intensity relationship among three components of fluctuating velocity, are also presented.

The specific sign of Reynolds shear stress in a turbulent boundary layer on a flat plate at zero incidence is a basic and classic feature before deducing the relation between the mean motion and the apparent stresses caused by the turbulent fluctuations. Generally, the Reynolds (shear) stress in a two-dimensional (2-D) boundary layer is defined as, whereis the fluid density andandare fluctuating velocity components along streamwise (x) and vertical (y) directions, respectively, as shown in Fig. 1. It has been given by a physical explanation to illustrate their occurrence in many literatures and textbooks [1-4]over several decades until now, as a traditional explanation, and also little investigated for the boundary-layer flow in a recent half century [5-7]. However, some questions are found out in such traditional explanation. It is very important because it reveals the intrinsic physical mechanism, such as the generation of Reynolds stress and its feature. Up to now, there are few published papers put the focus on solving them in recent several decades, as we know. Recently, the theory of vortex-induced vortex (VIVor), by introducing a vortex or vortex pair on or near the walls, is proposed to explain spacial characteristics of signs of resultant vorticity appeared in uniform and incompressible flow past a still bluff body [8]. According to the induced velocity fields, a new interpretation can be used more reasonably for such specific sign of Reynolds stress.

In order to clearly and correctly present the problem of specific sign of Reynolds stress, let us firstly review the traditional explanation [2]. In a turbulent stream, velocity components areu,v, andwalong with three own coordinatesx,y, andz, respectively. And a turbulent flow in mathematical terms is usually separated into a mean motion, denoted by the time-average of velocity, and, and into a fluctuation or eddying motion, denoted by its velocity of fluctuation, and. Then the timeaverages of the mixed products of velocity fluctuations, such as e.g.do, in fact differ from zero. The stress component, referred to as the Reynolds stress, can be interpreted as the transport ofx-momentum through a surface normal to they-axis. Considering, for example, a mean flow given bywith, as shown in Fig. 1,we can see that the mean productis different from zero: the particles which travel upwards in view of the turbulent fluctuation () arrive at a layeryfrom a region where a smaller mean velocityprevails. Since they do, on the whole, preserve their original velocity, they give rise to a negative componentin a layery. Conversely, the particles which arrive from above the layer () give rise to a positivein it. On the average,therefore, a positiveis “mostly” associated with a negativeand a negativeis “mostly” associated with a positive. We may thus expect that the time-averageis not only different from zero but also negative. The shearing stressis positive in this case, as shown in Fig. 2, and has the same sign as the relevant laminar shearing stress. This fact is also expressed by stating that there exists a correlation between the streamwise and vertical fluctuations of velocity at a given point.

From above analysis, there are some problems appeared as follows:

Question 1: Specific sign of Reynolds stress.

Fig. 1. Transport of momentum due to turbulent velocity fluctuation.

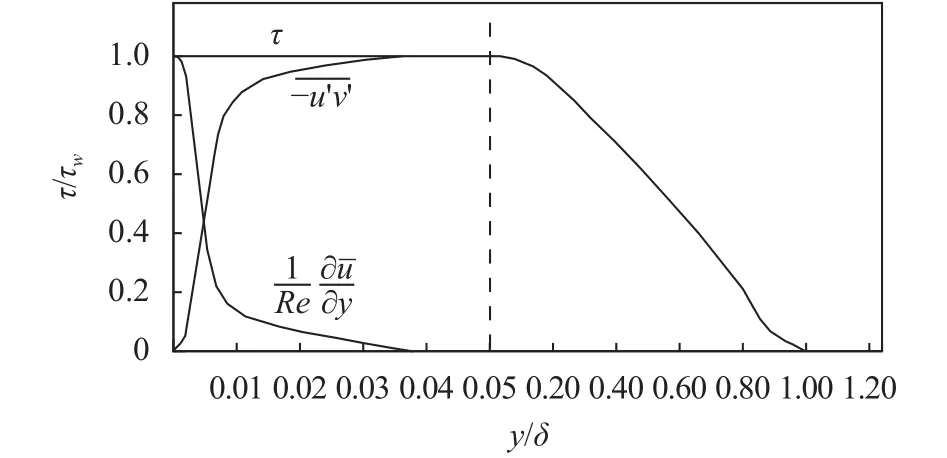
Fig. 2. Total stress scaled by, which is the shear stress at walls,non-dimensional Reynolds stress and viscous stressacross the boundary layer with the thickness in the flat plate at zero incidence without the pressure gradient (see Fig.22.14 in Ref. [1]).

A statement, the Reynolds stressis positive in the case of Fig. 1, is taken into account for further discussion in a different way under the basic assumption that the flow is incompressible. In a 2-D turbulent flow (only with velocity componentsand), the fluctuating components also satisfy the incompressible equation of continuity, i.e.. As shown in Fig. 1, given that only a fluctuation exists in a fluid element between top and middle square boxes, whenthen, we haveand. In such element, there is. However, it is already known that the turbulence is inherently a three-dimensional (3-D) unsteady fluid motion, as shown in Fig. 3. In a 3-D turbulent flow, through similar analysis, there is a problem: if given that a spanwise perturbationandwhenwould be positive and sodoes, due to the continuity equation. This analysis indicates that the spanwise fluctuationcould break the negative sign ofThere must be another means to solve this problem.

Question 2: Relationship between fluctuating and mean velocities.

As indicated by above traditional explanation, the streamwise fluctuating velocityis mainly determined by the difference of the time-averaged streamwise velocitybetween two successive layers along the vertical direction, not appeared as an independent part of decomposed turbulent motion. In other words, when the perturbed fluid element passes through, we haveis the vertical distance between such two layers anddenotes the fluid particle traveling upwards or downwards, respectively. Two direct deductions are naturally obtained. One isdisappeared theoretically in the uniform incoming flowor local flow region ofunder the assumption of isotropic turbulence, obviously inconsistent with the non-zero intensity of turbulence at the center of wind tunnel [2], as shown in Fig. 4. Another is its value would be gradually increased up to the maximum when the vertical distanceyapproaches the wall, still disagreed with the experimental measurements whatever for the turbulent boundary layer on a flat plate or a wind tunnel, as shown in Figs. 3 and 4. Furthermore, it is certainly confirmed that such explanation can not be applied for the appearance of vertical fluctuating velocityowning tois assumed to be appeared firstly along the stream.

Question 3: Intensity relationship among three components of fluctuating velocity.

Moreover, typically as shown in Fig. 3 or 4, also presented in recent work of Zhao et al. [10], it seems that there is an intensity relationship among these fluctuating velocity components, i.e., in the immediate neighborhood of the wall, which can not be verified in the traditional explanation.

Here the main aim is about to find out a new solution to answer above three questions through the analysis of velocity fields based on the theory of VIVor.

At first, in the turbulent flow, the Reynolds shearing stressexists not only in the turbulent boundary layer where the inertial forces are important, but also in the laminar sub-layer where the viscous forces dominate without any change of its specific sign, just as shown in Fig. 2. Only on the solid walls,for the non-slip boundary conditions of.Thereby, we can analyze such problem by the Stokes equation with negligible inertial forces in the laminar sub-layer at high Reynolds numbers.

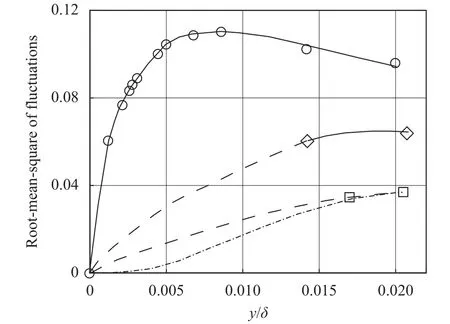
Fig. 3. Variation of the fluctuating turbulent velocity components in the boundary layer on a flat plate at zero incidence, as measured by Klebanoff [9], at a Reynolds number,where symbols,, and denotes non-dimensional measured values ofrespectively, dashed lines denote the variation from Klebanoff's viewpoint, and dash-dot line denotes the modified variation ofbased on the present study.

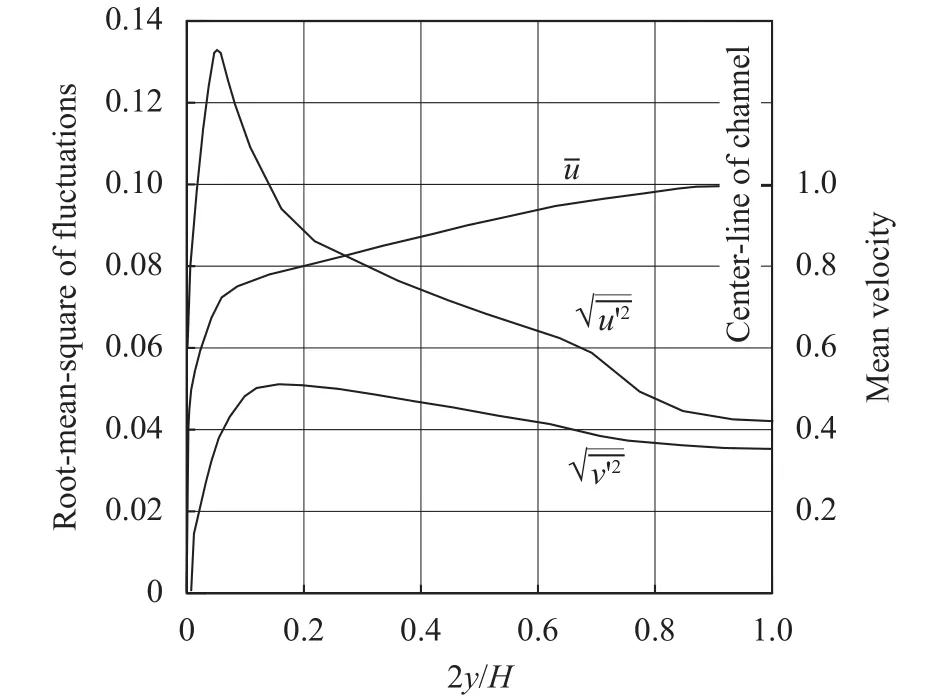
Fig. 4. Measurement of dimensionless fluctuating turbulent components, root-mean-square of streamwise fluctuationand vertical fluctuation and mean velocity in a wind tunnel (reported in Ref. [2], see Fig.18.3), where is the tunnel height.

Secondly, the induced velocity field,, resulted from the turbulence, is analyzed within a local spacial region and a quasi-steady time period without any change of fluctuating velocity sign. Only one spanwise wavelength of fluctuation is considered. The induced velocity componentsandin such local region are assumed to be almost uniformly distributed along the streamwisexdirection in present region. Such special distribution is associated with the eddy motion with small-scale streamwise vortex pair,. The streamwise vortex or vortex pair is not only almost uniformly distributed in the laminar sublayer but also in an approximate half period with same vorticity sign, such as a certain time periodorin Fig. 5. From this point, the induced velocity components,and, can be regarded as the result of Biot–Savart induction of such small-scale streamwise vortex or vortex pair caused by the turbulence within a certain time interval. The sketch of such small-scale turbulent flow is typically shown by the local flow above the upper surface of a flat plate at zero incidence in Fig. 6(a) or below the lower surface in Fig. 6(b).

On the other hand, the Reynolds stress or turbulence-induced streamwise vortex or vortex pair in the time intervalorcan be analyzed based on the definition of time-averaged value

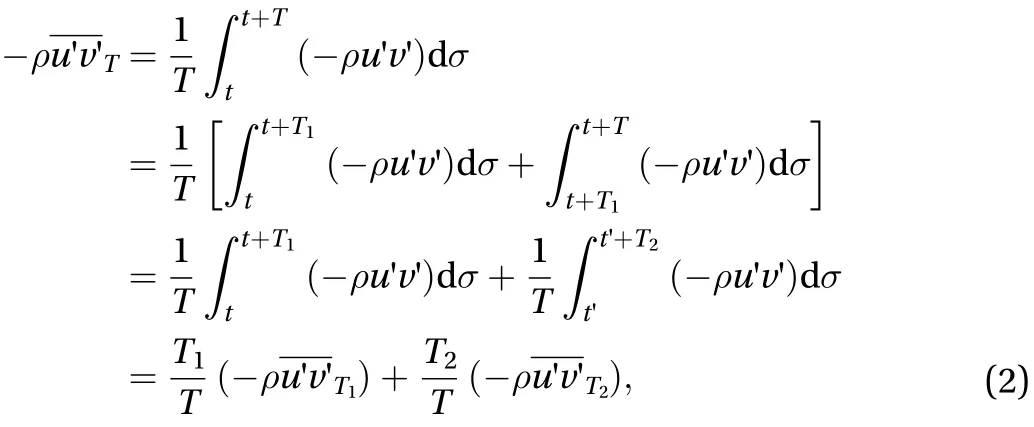
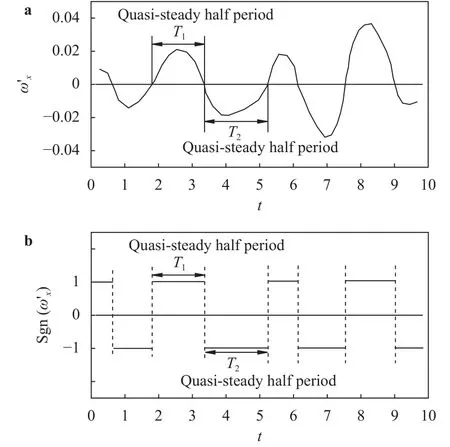
Fig. 5. Schematics of a time history of turbulence-induced streamwise vorticity at a certain position on or near the flat plate and b its sign varied along with the time.

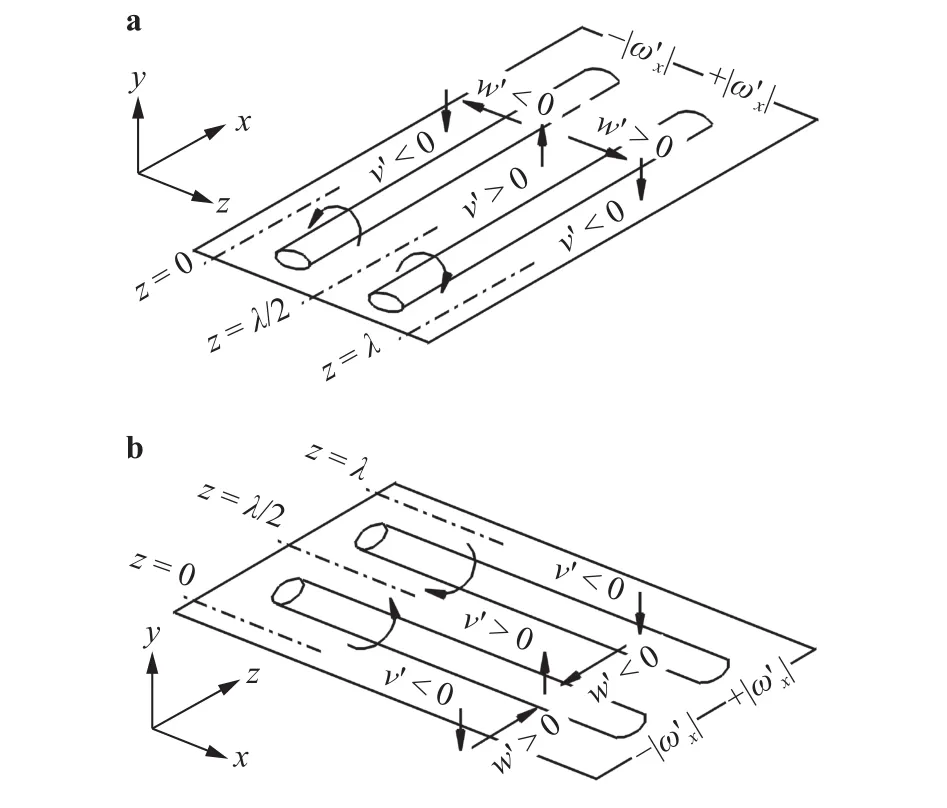
Fig. 6. Schematics of turbulence-induced streamwise vortex pairs with small-scale streamwise vorticity () and induced velocity field ( ) almost periodically varied along the spanwise direction on a upper and b lower surfaces of a flat plate at zero incidence.

Finally, the original point of local and inertial coordinate systemis taken as the start of above eddy motion. And thex-axis (streamwise) is always aligned with the local external flow,i.e. the downstream direction of streamwise velocity, they-axis (vertical) is the normal direction to the flat plate and thez-axis(spanwise) is the transverse parallel to wall. The small-scale eddies induced by the turbulent disturbance in the velocity field are assumed to be only evolved downstream in region ofand suppressed in region ofunder the effect of external flowwithin the region of, just as shown in Fig. 1. The physical mechanism is mainly attributed to the non-linear interaction between the external velocity fieldand induced vorticity field, i.e.in general vorticity equation. Even if the small-scale eddies evolve upstream temporally,such non-linear interaction would lead to these eddies convected downstream at last. The main reason is the turbulent perturbation just being temporal and unsteady, dislike the persistent and steady geometric disturbance [8].

Because of ignoring non-linear inertial forces, as a consequence, the principle of superposition of different velocity fields can be applied in solving the Stokes equation. Thus the local flow field in the laminar sub-layer can be divided into two parts. One is the 2-D external flow with mean velocity,, without any 3-D turbulent disturbance. Another is the resultant 3-D flow field with induced velocity.

Therefore, based on above assumptions and simplifications,the theory of VIVor [8] could be used to analyze the induced flow field in present case. For the incompressible flow with constant densityand kinematic viscosityof the fluid past the flat plate at zero incidence without consideration of any kind of nonconservative body forces and ignoring the energy transportation, the non-dimensional continuity and Stokes equations for induced velocity field in the laminar sub-layer are written out as follows

As shown in Fig. 6(a), the basic induced flow is investigated in the local region. An introduced streamwise vortex pair with opposite signs is started from, distributed uniformly along the +x-axis and periodically along thez-axis with the non-dimensional spanwise wavelength, and gradually disappeared far away from the flat plate. The induced velocity fields have following forms

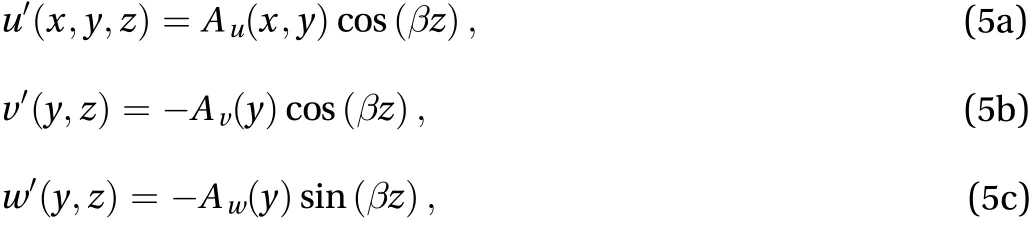
Substituting above Eq. (5) into the continuity equation,Eq. (3), we have the following relationship:with. And non-slip boundary conditions at walls request.

Therefore, exact solutions are obtained as a result of vortexinduced vortex, as reported in previous work [8]. In the present case, the intensity of induced streamwise vorticitydistributed on the wall is. Then we have the following solutions

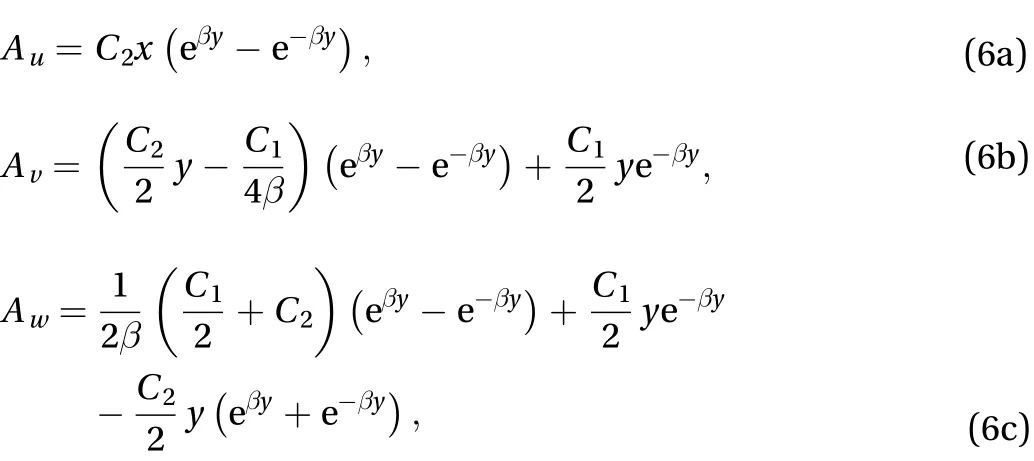
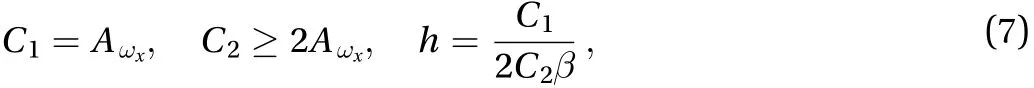
wherehis the effective height of above solutions in the immediate neighborhood of wall, i.e.. It at least shows that when the spanwise scale of small eddiesis reduced, the effective heighthis also reduced linearly and irrelevant to the strength of streamwise vorticity on the wall.

(1) Answer to Question 1: Specific sign of Reynolds stress

Consequently, according to the exact solutions, Eq. (6), we have the following proof as the new interpretation different from the traditional explanation in the specific sign of Reynolds stress.From Eqs. (5) and (6), the third sign law for streamwise and vertical components of induced velocity,and, respectively, by introducing the third sign variable,, as reported in Ref.[8], is obtained as follows

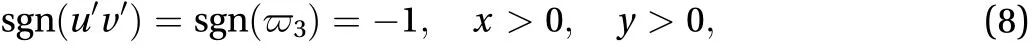
except some special positions, e.g.and, at which, and where sgn is the sign function. In addition,below the flat plate in region ofand, as shown in Fig.6(b), the third sign variable is always positive,[8].

As a result, in present special local region, we can draw the conclusion that the Reynolds stressis always positive theoretically based on the analysis of Eq. (8) in the external shear flow like Fig. 1, except some special positions with. The positive Reynolds stress is independent of the spacial distribution of induced spanwise velocity, the spanwise wavelengthand Reynolds number, indicating that such relationship is an intrinsic physical mechanisms in the turbulent boundary layer on the flat plate.

(2) Answer to Question 2: Relationship between fluctuating and mean velocities

Based on the above analysis and third sign law, we can clearly identify the relationship between fluctuating and mean velocities. First of all, the streamwise fluctuating velocity, as well as the Reynolds stress, is intrinsically generated by 3-D turbulence or turbulence-induced small-scale eddies, rather than the interaction between the turbulent fluctuation () and mean velocity () in the traditional explanation. And their appearance is irrelevant to the gradient of local mean flow,whatever for its profile withor. It is already known that the effect of inertial forces is mainly the convection and stretching of vorticity [11]. Therefore, as stated before, the effect ofis the determination of perturbed small-scale eddiesthrough the term, as well asthrough the term, convected and evolved along the downstream direction of local mean flow. Then the sign of Reynolds stress,as well as the sign of, is just followed by the downstream direction of mean flow, or a result of interaction between those smallscale eddies and external mean flow under the inertial effect.

Moreover, a hypothesis could be proposed here for brief discussion. The Reynolds stress with a positive sign in the boundary layer on a flat plate at zero incidence could be mainly attributed to small-scale eddies with a positive shearing stress firstly appeared in the laminar sub-layer due to the turbulence. These small-scale eddies are evolved into horseshoe and hairpin vortices, convected downstream and away from the wall under the inertial forces. Finally it leads to the whole turbulent boundary layer full of vortices with such positive shearing stress. It would be studied in future work. At least, it is already confirmed that the above third sign law foris also valid when the streamwise vortices leave the wall in previous work [8].

(3) Answer to Question 3: Intensity relationship among three components of fluctuating velocity

As shown in Fig. 7(a) as an example with, there are different features in variations of three amplitudes of induced velocity components in the local region.

Now let us check the intensity relationship among them. Figure 7(a) at least presents thatis certainly greater than. Or we can solve the problem through the analysis of Eq. (6) as follows

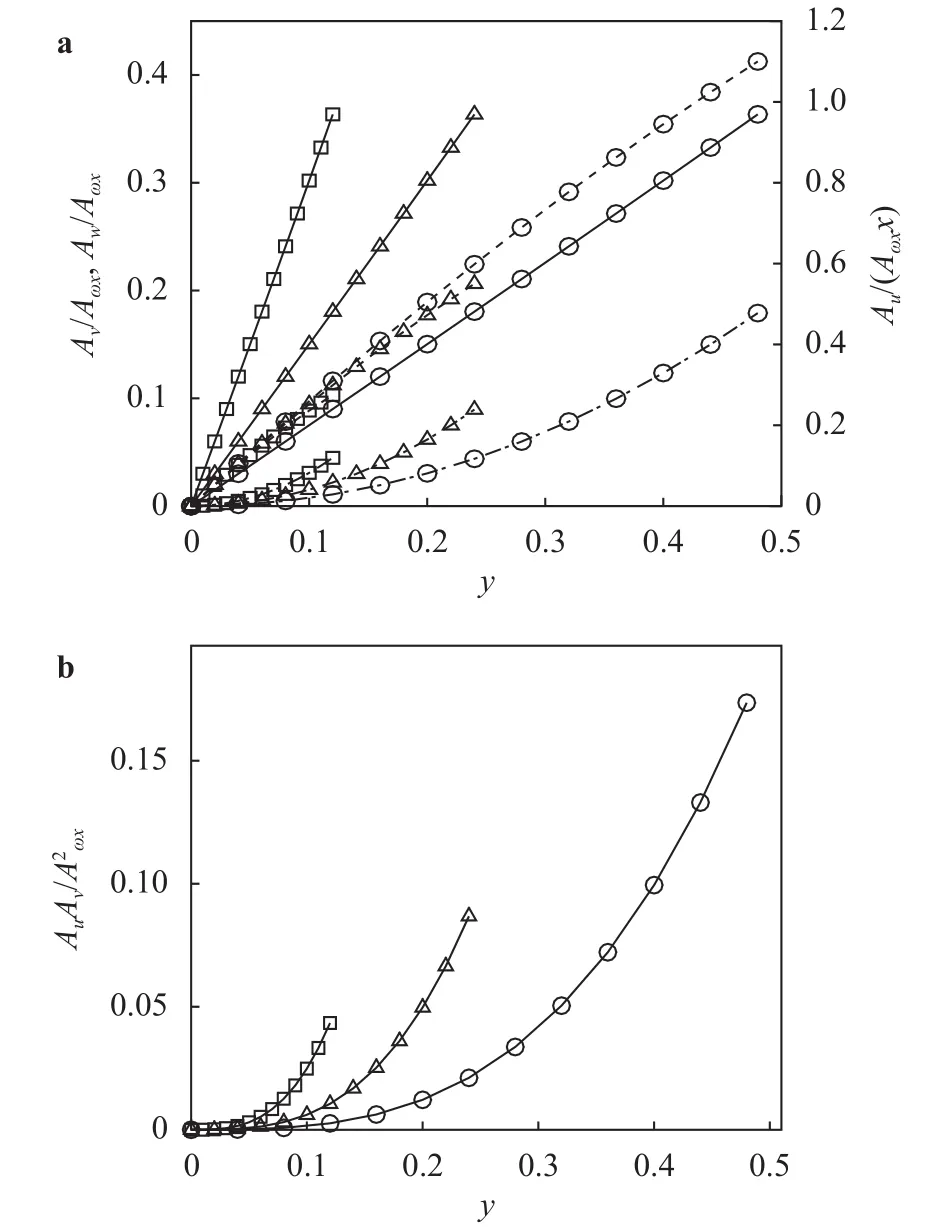
Fig. 7. Scaled amplitudes of a three components of fluctuation velocity, , and b turbulent shearing stress, , varied along the vertical position y with , where solid, dash-dot and dashed lines in a denote, respectively, while symbols,and denote the wavelength, and, respectively.

Here, it is also interestingly found out that there is the following relationship under the previous conditions:.

Meanwhile, the variation of amplitude of Reynolds stress,, as shown in Fig. 7(b), is also well agreed with the previous experimental measurements in Fig. 2. Moreover, if we take a first-order approximation ofby a power series expansion about, Eq. 6(a, b) provide the following behaviors

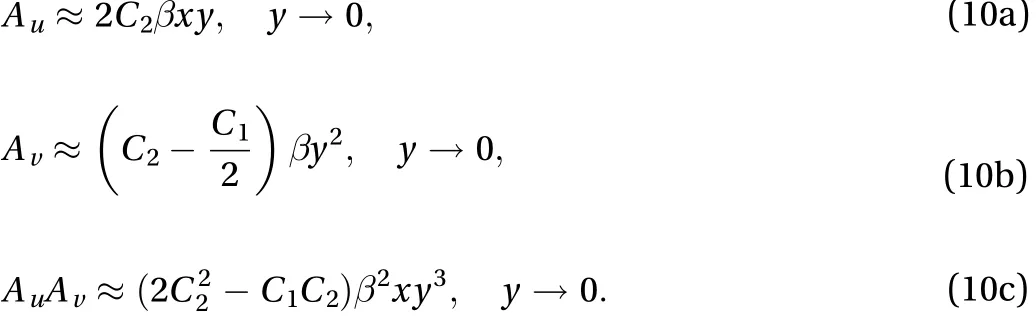
They are also exactly agreed with the previous results:and, and then[11].

Besides, by comparison with Figs. 4 and 7(a), the variation of amplitude ofnear the wall is different. From the point of continuity equation, Eq. (3),on the wall should be equal to zero becauseandare all zero on the smooth wall,just as shown in Fig. 7(a), rather than the non-zeroat wall in Fig. 4.

In the present paper, the specific sign of Reynolds stress in the boundary layer on a flat plate at zero incidence is firstly interpreted by the relation between the mean and fluctuating flows due to the transport of momentum. However, the theory of vortex-induced vortex proposed recently is also successfully to explain such character of Reynolds stress. The flow analysis is carried out by introducing small-scale streamwise vortices, as turbulent eddy motion, in the immediate neighborhood of the flat plate.

At first, it is theoretically confirmed that the Reynolds stress in present case is always positive, as indicated by the third sign law for streamwise and vertical components of fluctuating velocity. Such sign relationship is an intrinsic physical mechanism in the turbulent boundary layer, irrelevant to the distribution of spanwise fluctuating velocity, the spanwise wavelength of small eddies and Reynolds number.

Then such new interpretation illustrates that the generation of Reynolds stress, as well as the streamwise fluctuating velocity,is intrinsically independent of the mean flow. But its specific sign, or its evolution, would be determined by the mean flow due to the inertial forces.

Finally, the intensity relationship among three components of fluctuating velocity in the local flow region observed in experimental measurements,, is theoretically verified too.

Verily to say, it is hard to establish the universal representation of Reynolds stress because such stress is really and closely related to the local flow region and small-scale eddies with different spanwise wavelengths induced by the turbulence.

Acknowledgements

This work was financially supported by the Strategic Priority Research Program of the Chinese Academy of Science (Grant XDB22030101).