Vibration of two-dimensional hexagonal boron nitride
2018-02-13JianpengYiLifengWangYiqingZhang
Jianpeng Yi, Lifeng Wang*, Yiqing Zhang
State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
Keywords:Hexagonal boron nitride Molecular dynamics Natural frequency Electric field
A B S T R A C T The dynamic behavior of two-dimensional nanostructures is important to the future application of nano devices. The vibrational behaviors of single-layered hexagonal boron nitride (h-BN) are studied by molecular dynamics simulation and continuum plate model. The bending stiffness and Poisson's ratios of h-BN along zigzag direction and armchair direction are calculated. H-BN is softer compared with graphene. The continuum plate model can predict the vibration of h-BN with four edge-clamped boundary conditions well. The electric fields in different directions have obvious influence on the vibration of h-BN. The natural frequency of h-BN changes linearly with the electric field intensity along the polarization direction. The natural frequency of h-BN decreases with the increase of electric field intensity along both positive and negative nonpolarization direction. While the natural frequency of h-BN increases with the increase of electric field intensity along both positive and negative transverse electric field.
Two-dimensional nanostructures draw much attention due to their structural characteristics and potential applications.Hexagonal boron nitride (h-BN) not only has similar Young's modulus and strength as graphene [1], but also has strong oxidation resistance and thermal stability [2].H-BN is a semiconductor material with a wide band gap of 5.3-5.9 eV [3, 4] which can be changed by hydrogenation. Wu et al. [5] designed a resistive switching device based on the multilayerh-BN, which is expected to mimic the synaptic weight changes in neuromorphic systems. A linear humidity sensor was fabricated by using the composite materials of polyethylene oxide andh-BN, they found that it has good stability and sensitivity [6].H-BN is considered as one of the most ideal materials for synthesizing heterogeneous structures with graphene, transition metal sulfides and other two-dimensional materials, which has great potential in the fields of microelectronics, photoelectricity and detection in the future.
The mechanical properties and structure ofh-BN have been widely studied. Bosak et al. [7] investigated the elastic modulus of single-crystallineh-BN using inelastic X-ray scattering at room temperature. Their experimental results consist with the predictions ofab initiocalculations . Li et al. [8] measured the bending modulus of single-crystallineh-BN using three-point bending tests in an atomic force microscope. They suggested that the change of bending modulus with thickness was due to the layer distribution of stacking faults. Slotman and Fasolino [9]studied the structural properties of single-layeredh-BN by molecular dynamics (MD) simulations. They analyzed the height fluctuations and put forward that the bending modulus ofh-BN equals to 8.6518×10-20N·m at zero temperature which is lower compared with graphene. However, using different fitting parameters of Tersoff potential, Singh et al. [10] obtained the bending modulus ofh-BN is 1.3779×10-19N·m. Ansari et al. [11] investigated the influence of electric field on the mechanical properties by density functional theory calculation. Their results showed that the size and directions of electric field have great effects on Poisson's ratio and Young's modulus.
As the structure size reaches to nanometer scale, the size effect and quantum effect make the material possess different properties from the macroscopic one. So the dynamics of the nanostructure requires further study. Lopez-Suarez et al. investigated the nonlinear energy harvesting devices based onh-BN under compressive strain by performing ab initio calculations and solving a Langevin equation [12]. Chandra et al. [13] analyzed the effects of tube lengths and temperature on the vibrational spectrum of armchair-type BN nanotubes by MD simulation. Liu and Wang [14] studied the thermal vibration of carbon nanotubes by semi-quantum MD method. They found that the thermal vibrational spectrum obtained by semi-quantum MD is significantly smaller than that obtained by classical MD simulation. Jiang et al. [15] investigated the thermal vibration of singlewalled carbon nanotubes bridged on a silicon channel by establishing three-segment Timoshenko beam model and one-segment Timoshenko beam model with elastic boundaries. Their results of MD simulation showed that both models can predict the vibrational behaviors of single-walled carbon nanotubes well. Liu and Wang [16] studied the vibrational behaviors of zinc oxide nanowires by MD simulation and continuum beam model.They found that the natural frequency was significantly affected by the size effect and electric field. Zhang et al. [17] investigated the vibrational behaviors of monolayer black phosphorus using MD simulation and the orthotropic plate model.
The vibration of piezoelectric plate has potential application in the field of microelectromechanical manufacturing.H-BN possess obvious piezoelectric response because its sublattices are occupied by nitrogen atoms and boron atoms alternately,which breaks the reverse symmetry of the structure [18]. Based on the nonlocal theory and differential quadrature method, Ke et al. [19] studied the free vibration of rectangular piezoelectric plates. Liu et al. [20] investigated the buckling and post-buckling behaviors of piezoelectric nanoplate based on the nonlocal Mindlin plate model. Yamakov et al. [21] studied the piezoelectric properties of boron nitride nanotubes through introducing a strain-dependent potential term of dipole in the classical MD model. They pointed out that this model can take the triple symmetry of piezoelectric tensor ofh-BN into account based on the properties of interatomic potential and fitting parameters. Zhang and Meguid [22] analyzed the piezoelectric properties of the multi-walled boron nitride nanotubes by building an electric field force model based on the Tersoff potential using MD simulation. To our best knowledge, however, there is little research on the vibration of two-dimensionalh-BN. In this letter, the mechanical properties and vibration behavior ofh-BN are investigated by plate model and MD simulation.
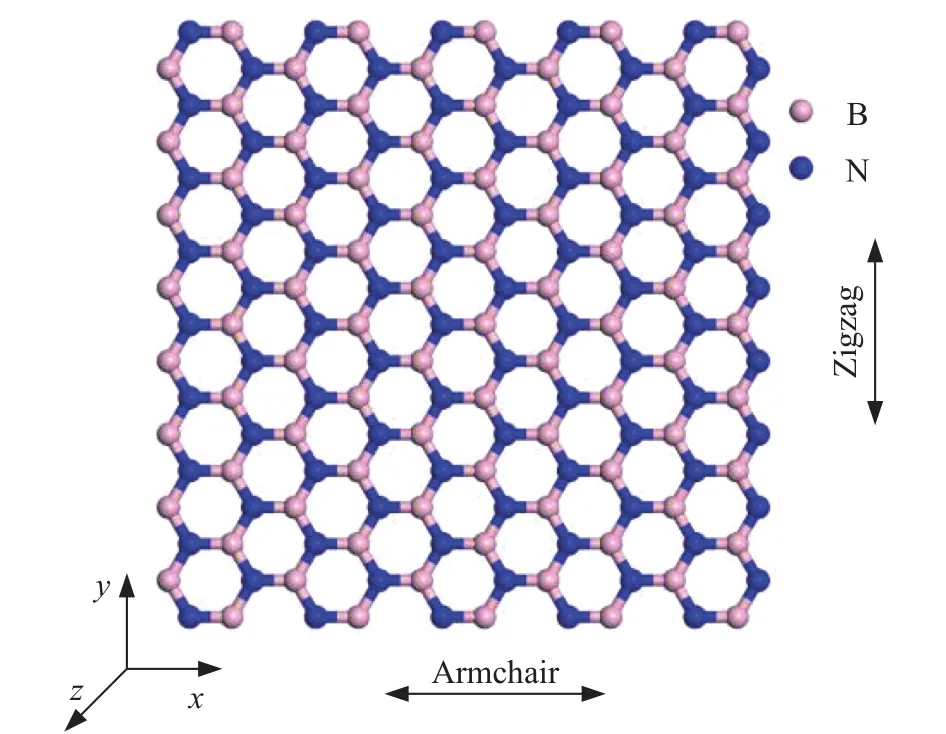
Fig. 1. Atomic structure of hexagonal boron nitride.
To study the vibration of two-dimensionalh-BN, the mechanical parameters of two-dimensionalh-BN should be obtained first. The atomic structure ofh-BN is shown in Fig. 1, in which nitrogen atoms represented by dark blue point and boron atoms represented by light gray one are arranged alternately. A rectangular cell ofh-BN with length and width along the armchair and zigzag direction is created.H-BN is a strictly two-dimensional structure. The thickness of monolayerh-BN is assumed to be 0.333 nm [23]. MD simulations are performed using LAMMPS[24] in this work. The Tersoff potential [25] used to describe the interatomic interaction can be written as
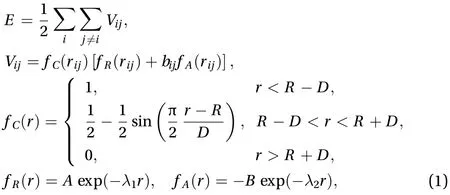
whererijis the interatomic distance,fCis a cutoff term to guarantee first neighbor interaction,fRis repulsive interaction andfAis attractive interaction.
Based on experimental research and simulation fitting, Sevik et al. [26] and Kinaci et al. [27] have proposed parameters of the Tersoff potential that satisfied the properties ofh-BN. They have well simulated the thermal conduction characteristics ofh-BN nanostructures. Many researches have studied the mechanical and structural properties ofh-BN through the modified Tersoff potential, which is in good agreement with the experimental results.
According to the energy difference of structural bending deformation, the bending stiffness ofh-BN is defined as

whereDis the bending stiffness ofh-BN,eis the bending strain energy per unit area. Here,κ=1/ris the curvature andris the radius of single-walled BN nanotubes. The single-walled BN nanotube can be obtained by crimping monolayerh-BN and they have the same geometrical parameter.
A series of single-walled BN nanotubes with different radiuses are sufficiently relaxed by MD simulations. Periodic boundary conditions are applied to eliminate the influence of dimensions and boundaries. As shown in Fig. 2, the bending stiffness of zigzag-type and armchair-typeh-BN atT=0 K are 1.4259×10-19N·m and 1.4195×10-19N·m respectively, which is consistent with the results obtained in paper [10] and significantly less than that of graphene at 2.8999×10-19N·m [28]. For simplicity, the bending stiffness ofh-BN is chosen as 1.42×10-19N·m.
The axial tension simulation ofh-BN with length of 15.0 nm and width of 14.9 nm is performed by MD simulation. The transverse strain and axial strain ofh-BN are calculated after full energy relaxation. The Poisson's ratio can be determined by the ratio between transverse strain and strain along stretch direction of theh-BN. Figure 3 shows that the average Poisson's ratio of zigzag-type and armchair-typeh-BN are 0.31 and 0.29, respectively. For simplicity, the Poisson's ratio is chosen as 0.3.
By analyzing the mechanical parameters ofh-BN obtained using MD simulations, single-layeredh-BN can be considered as an isotropic structure. The Kirchhoff plate model with four edgeclamped is established. The solution can be obtained by the finite element method (FEM). The free vibration equation of thin plate with bidirectional initial stress is
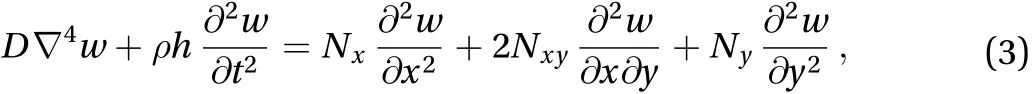
whereD,andhare bending stiffness, density and thickness,respectively.NxandNyare the initial stress alongx-axis andyaxis. Since the magnitude ofNxyis significantly smaller than that ofNxandNyin MD simulation, the effect ofNxycan be ignored by taken as zero.
The vibration amplitude of the thin plate is assumed as

The boundary condition with four edge-clamped is

The potential energy and kinetic energy of the thin plate can be expressed as
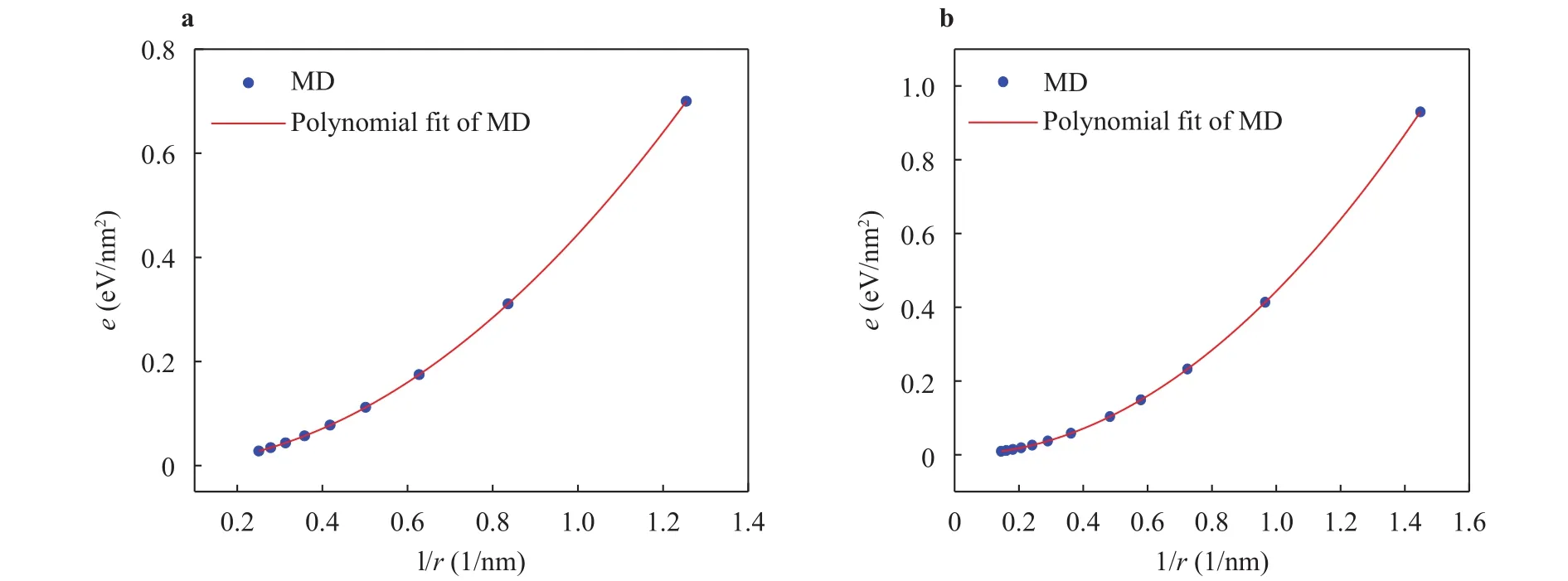
Fig. 2. Bending stiffness of h-BN: a zigzag type; b armchair type.
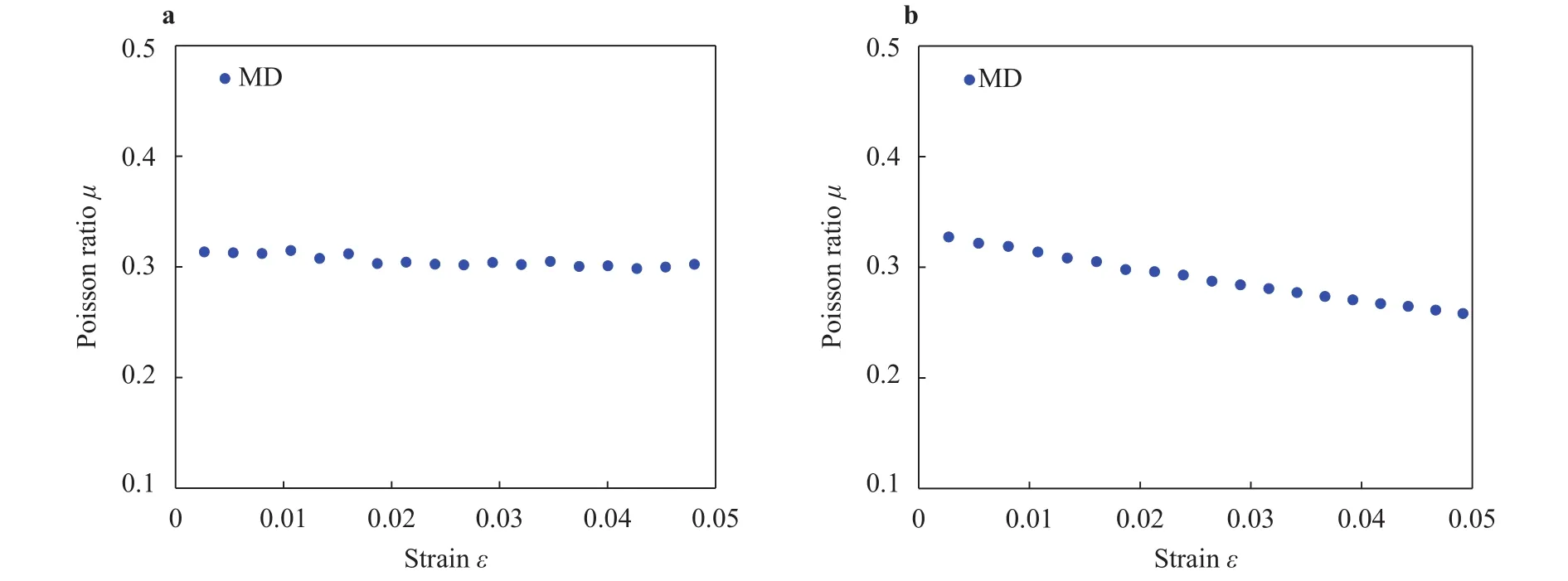
Fig. 3. Poisson's ratio of h-BN: a zigzag type; b armchair type.
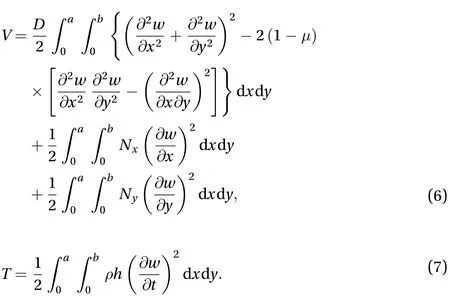
Substituting Eqs. (7) and (8) into the following variation equation

The displacement functionW(x,y) is expressed as
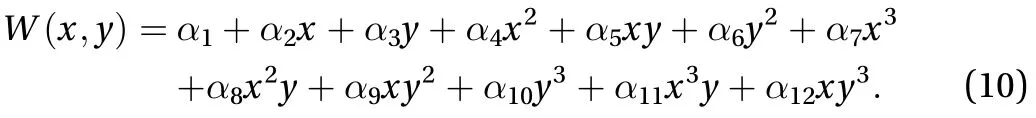
The node displacement of the element is expressed as
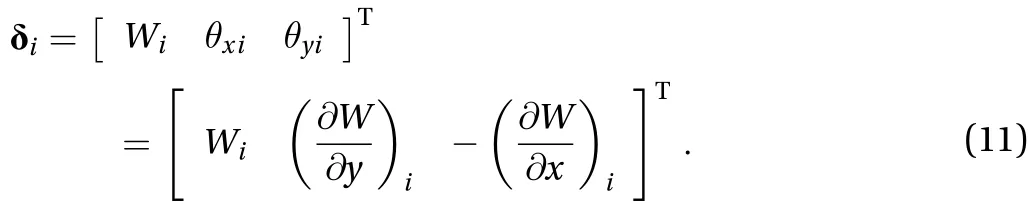
One can introduce the isoparametric coordinatesand,where,, 2aeand 2beare the length and width of rectangular element, respectively. The displacement function can be transformed as

The bending elastic matrix of thin plate is
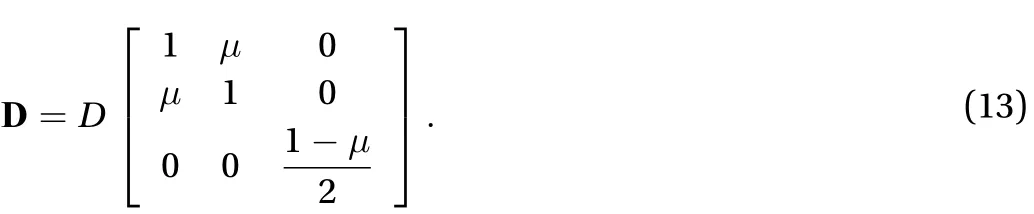
The element stiffness matrix can be obtained
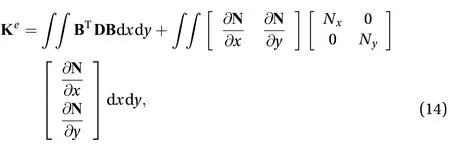
where the geometric matrix is
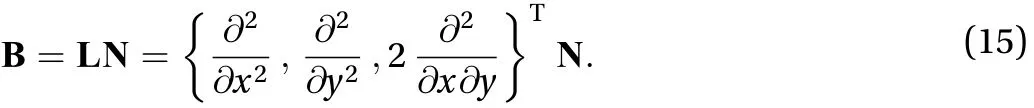
The element mass matrix can be obtained

Combining the element stiffness matrix Keand the element mass matrix Meinto the integral stiffness matrix K and the integral mass matrix M, one can obtain

The natural frequency of the Kirchhoff plate model with four edge-clamped can be obtained by Eq. (17).
MD simulation is performed to analyze the vibrational behaviors ofh-BN in canonical (NVT) ensemble, and the temperature of the system is controlled by Nose-Hoover thermostat. All simulation processes run 10 ns with time step set as 1 fs. Anh-BN model with length of 6.79 nm and width of 5.26 nm is established. The atoms of the outermost two layers are fixed. Simulations are carried out under temperatureT=30 K, 90 K, 150 K, 225 K and 300 K. It can be seen from Fig. 4 that the natural frequency ofh-BN increases slightly with the increase of temperature, which is mainly caused by the negative expansion coefficient ofh-BN [29]. The models with the width of 5.26 nm are es-tablished to study the influence of size on the natural frequency ofh-BN. Figure 5(a) shows that the natural frequency ofh-BN decreases with the increase of length. Similarly, as shown in Fig.5(b), the frequency of thermal vibration ofh-BN with length of 5.78 nm has the same tendency. From the comparison between MD and FEM in the Figs. 4 and 5, we can observe that the results via two methods are consistent with each other. It shows that the Kirchhoff plate model can predict the vibration of single-layeredh-BN well. In addition, the parameters obtained using MD simulations reflect the natural properties ofh-BN and are reliable to apply in the FEM.
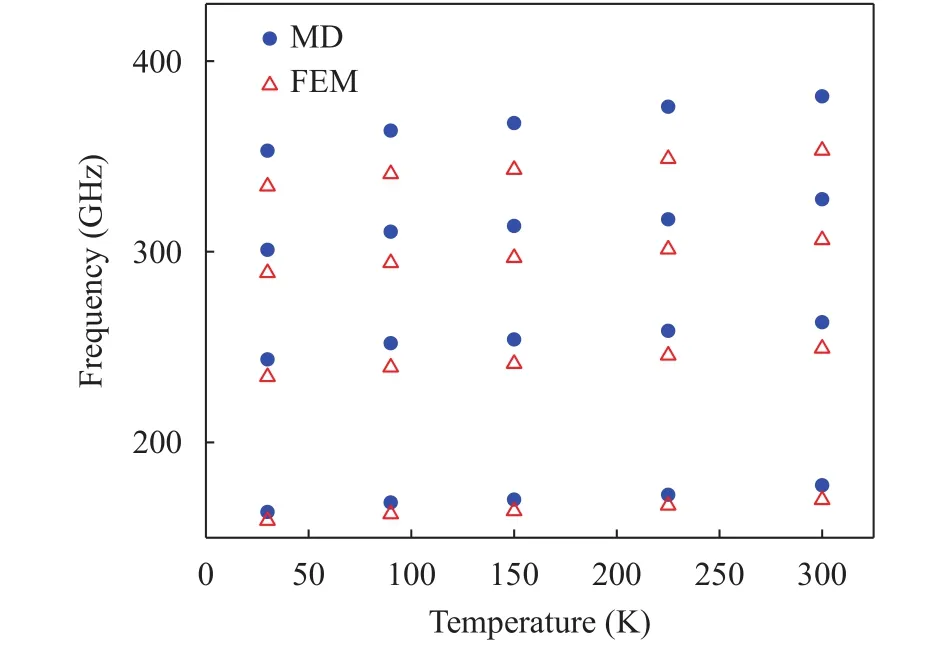
Fig. 4. Influence of temperature on the natural frequency.
H-BN has tensile piezoelectric properties along the polarization direction and shear piezoelectric properties along the nonpolarization direction. The ioniciwith charge ofqiis subjected to a forceFi=qiEin electric field [22], where the effective charge of boron ions and nitrogen ions are set as +2.6eand -2.6e[30], respectively. As shown in Fig. 6(a), when a positive electric field is applied, the compression deformation occurs. Inversely, tensile deformation occurs. The stress inxdirection decreases linearly with the increase of positive electric field. In Fig. 6(b), shear deformation occurs due to electric field in non-polarization direction. The stresses in bothxdirection andydirection increase with the raising of the intensity of electric field of both positive case and negative case, while the shear stress changes very small.
In order to analyze the effects of electric field on thermal vibration ofh-BN, anh-BN model with length of 8.53 nm and width of 5.26 nm is established. MD is performed usingNVTensemble and the temperature is set as 30 K. Figure 7(a) shows the directions of electric fields applied toh-BN model. In Fig. 7(b),the natural frequencies ofh-BN change linearly with the electric field intensity, when the in-plane electric field along the polarization direction (Ex) increases from -1.0 V/nm to 1.0 V/nm. Figure 7(c) shows that the natural frequencies ofh-BN decrease with the increase of electric field along non-polarization direction (Ey) of both positive case and negative case, while Fig. 7(d)shows that the natural frequencies ofh-BN increase with the increase of transverse electric field (Ez) of both positive case and negative case.

Fig. 5. Influence of size on the natural frequency: a as the length changes; b as the width changes.
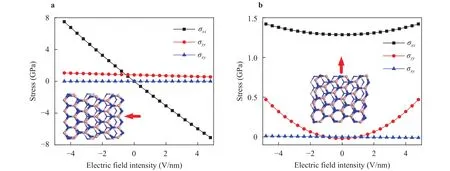
Fig. 6. Variation of stress under electric fields.
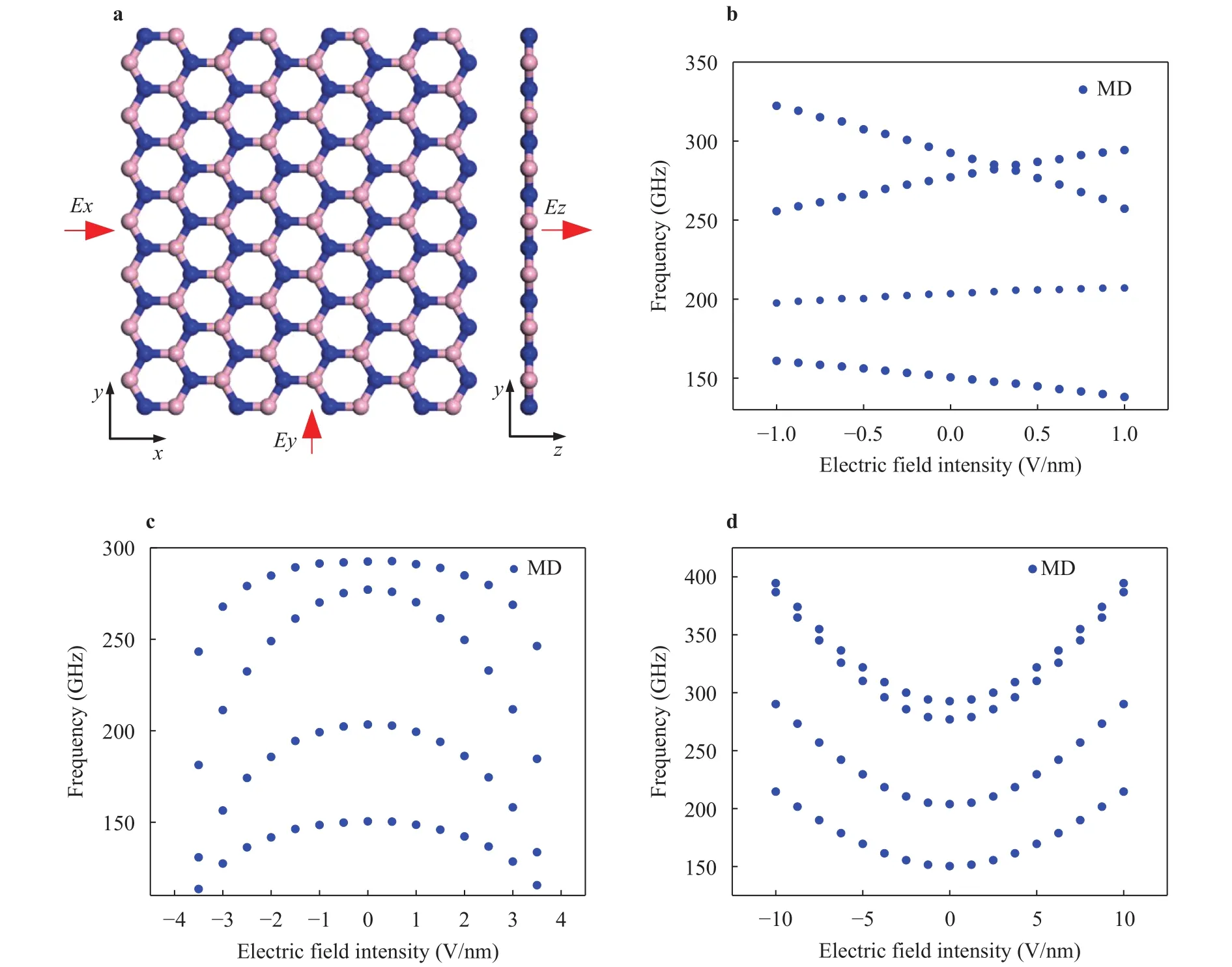
Fig. 7. Effects of the electric field intensity on the natural frequency: a direction of the electric field; b polarized direction (Ex); c non-polarization direction (Ey); d transverse direction (Ez).
In conclusion, the vibrational behaviors of monolayerh-BN are studied by MD simulation and continuum plate model. The results demonstrate that the bending stiffness and the Poisson's ratios ofh-BN have almost the same values on the armchair and zigzag direction.H-BN is softer compared with graphene. The?continuum plate model can predict the vibration ofh-BN with four edge-clamped boundary conditions well. The electric fields in different directions have obvious influence on the vibration ofh-BN. The natural frequencies ofh-BN change linearly with the electric field intensity along the polarization direction. The natural frequencies are no longer linear with the increase of nonpolarization electric field and transverse electric field.
Acknowledgements
This work was supported in part by the National Natural Science Foundation of China under Grants 11522217 and 11632003,in part by 333 Talents Program in Jiangsu Province, in part by the Natural Science Foundation of Jiangsu Province under Grant BK20171411, and in part by the Fundamental Research Funds for the Central Universities of China.
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Data-driven computing in elasticity via kernel regression
- The effects of mean sea level rise and strengthened winds on extreme sea levels in the Baltic Sea
- New interpretation of specific sign of Reynolds stress in the boundary layer on a flat plate
- An improved smoke-wire flow visualization technique using capacitor as power source
- Head-on collision between two hydroelastic solitary waves with Plotnikov-Toland's plate model
- Linear, nonlinear dynamics, and sensitivity analysis of a vibratory ring gyroscope
