Structure-preserving approach for infinite dimensional nonconservative system
2018-02-13WeipengHu
Weipeng Hu*
School of Civil Engineering and Architecture, Xi'an University of Technology, Xi'an 710048, China
Keywords:Structure-preserving approach Generalized multi-symplectic Hamiltonian Nonconservative system Non-smooth model
A B S T R A C T The current structure-preserving theory, including the symplectic method and the multisymplectic method, pays most attention on the conservative properties of the continuous systems because that the conservative properties of the conservative systems can be formulated in the mathematical form. But, the nonconservative characteristics are the nature of the systems existing in engineering. In this letter, the structure-preserving approach for the infinite dimensional nonconservative systems is proposed based on the generalized multi-symplectic method to broaden the application fields of the current structure-preserving idea. In the numerical examples,two nonconservative factors, including the strong excitation on the string and the impact on the cantilever, are considered respectively. The vibrations of the string and the cantilever are investigated by the structure-preserving approach and the good long-time numerical behaviors as well as the high numerical precision of which are illustrated by the numerical results presented.
The structure-preserving idea originated from the symplectic method proposed on the Proceeding of the Symposium on Differential Geometry and Differential Equations by Feng [1] in 1984. The main idea of the symplectic method is designing the difference scheme that can preserve the symplectic structure of the finite dimensional Hamiltonian dynamic system formulated in the following canonical form
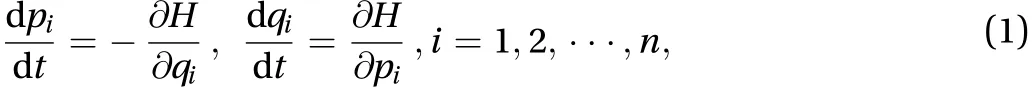
The canonical form Eq. (1) was considered in the early structure-preserving method because that it owns remarkable elegance and symmetry, which was first introduced by Hamilton in 1824 as a general mathematical scheme for problems of geometrical optics. This approach was then successfully applied by Hamilton himself in 1834 to an entirely different area—analytical dynamics.
Why did the symmetries of the dynamic systems be highly regarded in the structure-preserving approach? It has been proved that the symmetries of the dynamic behaviors for the mechanical systems are mapped to the symmetries of the Lagrangian function. For example, the translation invariance for the physical law resulting from the uniformity of the space is reflected as the translation invariance of the Lagrangian function respect to the generalized coordinates, which is the well-known momentum conservation law. The translation invariance for the physical law resulting from the uniformity of the time is reflected as the translation invariance of the Lagrangian function respect to the time, which is the well-known energy conservation law. The translation invariance for the physical law resulting from the isotropy of the space is reflected as the rotation invariance of the Lagrangian function respect to the generalized coordinates, which is the well-known angular momentum conservation law. The above examples imply that, one can deduce a series of important conservation laws from the symmetries of the dynamic models even though the dynamic models are too complex to obtain the analytical solutions of them. In addition, some new solutions of the dynamic models can be found from a known solution if the symmetries of the models are considered.For the numerical simulation, the most significant contribution of the symmetry is that, all the symmetries of a certain system are preserved and the simulation efficiency of the numerical method can be improved drastically when one of symmetries is preserved in the numerical simulation.
The mathematical description of the symplectic method withdraws the applications of which in the engineering. Thus,Zhong [2, 3] restated the symplectic method taking the spring oscillator as an example and introduced the symplectic method into computational mechanics. It has been proved that the symplectic method owns excellent long-time numerical stability for the finite dimensional conservative Hamiltonian system. But, for the infinite dimensional system, the local dynamic behaviors are more important and the associated symmetries cannot be preserved in the symplectic method framework. Thus, the multisymplectic theory was proposed by Bridges [4, 5] and Marsden et al. [6], in which, the space-time symplectic structure of the Hamiltonian partial differential equation (PDE) to improve the local structure-preserving characteristics [7] of the numerical method.
Both the symplectic method and the multi-symplectic method are based on the idealized conservative Hamiltonian systems.But, nonconservative factors almost exist in all mechanical system, some of which should not be neglected because that some important nonlinear characteristics of the mechanical system result from the nonconservative factors. Thus, for the infinite dimensional Hamiltonian system with the weak damping, the generalized multi-symplectic approach [8, 9] was proposed and some preliminary applications [10–14] were reported subsequently. In this letter, the structure-preserving method based on the generalized multi-symplectic theory will be introduced for the infinite dimensional nonconservative system briefly and the application on two simply examples will be presented.
It is needed to clarify that the limitation of the generalized multi-symplectic approach [8, 9] is the assumed tiny damping in the dynamic system. Actually, the structure-preserving method is an open framework idea that should be generalized to the system containing strong nonconservative factors.
The system containing strong nonconservative factors may own some conservation laws except for the conservation of the energy. For example, the mass of all nonconservative systems in the framework of the classic mechanics is a conserved quantity;the volume of the incompressible fluid is another conserved quantity; the momentum of the idealized collision system is also a conserved quantity. Although the contributions of preserving these conservation laws cannot be told now, it is an unquestioned fact that the employment of the structure-preserving idea in the simulation of nonconservative systems can improve the long-time numerical stability [10, 11, 13, 15]. Thus, it is necessary to broaden the structure-preserving theory to the infinite dimensional system with significant nonconservative factors in this letter.
Reconsider the Hamiltonian PDE with the weak damping in the first-order form [9]
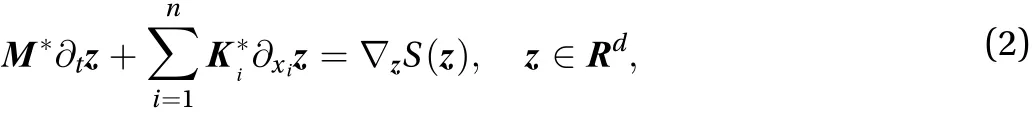
With the matrix decompositionandthe multi-symplectic residual can be obtained
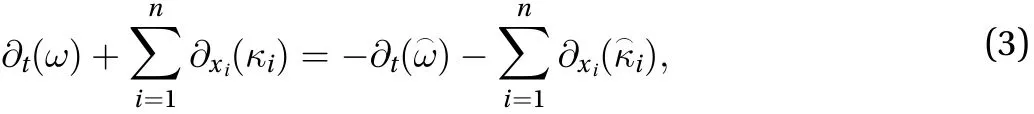
In my previous work [9], the generalized multi-symplectic integrator was defined as the difference scheme with the truncation error that is no less than the discrete value of the multi-symplectic residual in each time step to avoid the symmetry breaking problem of the Hamiltonian PDE with the weak damping.
In this letter, two examples with the strong nonconservative factors will be given to remove this limitation in the following numerical experiments.
The structure-preserving method for the excited string was first proposed in Ref. [16]. The vibration of the excited string will be reconsidered, which can be formulated as

The approximate symmetric form (Eq. (2)) withcan be obtained by defining the state variablewiththe quasi Hamiltonian functionthe matricesand
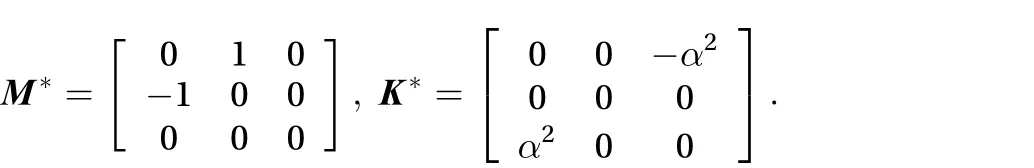
This form is not a standard multi-symplectic form because that the functionincludes time and space variables explicitly.
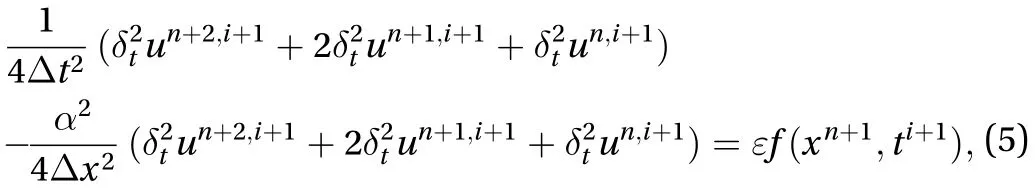
In the numerical simulations, the time step length and the space step length of the scheme (Eq. (5)) areandrespectively. The wave speed is fixed atthe length of the string is assumed as, the initial conditions and boundary conditions are given by
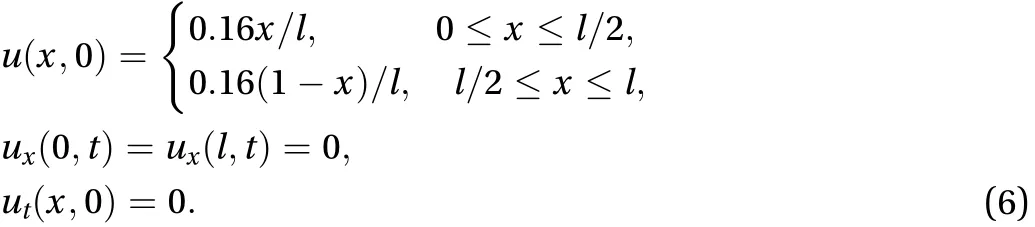
Simulation on the evolution of the string with the given excitation formulated asis proceed. Figure 1 shows the relative error of the total energy (the total energy of the beam isin the intervalbetween the numerical solution and the analytical solutionFrom Fig. 1, it can be found that the relative error of the total energy between the numerical results and the analytical solution is tiny and decreases with the time elapse,which implies that the scheme (Eq. (5)) can reproduce the energy evolution of the excited string well in a long time interval.
The impact on the structures is very common in engineering.As a special kind of excitation, the impact load results in the non-smooth dynamic model of the system. The analysis on the non-smooth model is a challenge for a long time. The structurepreserving method developed in my previous work [9] is just focusing on the local dynamic problem. Thus, the following dynamic model that describing the vibration of the cantilever subjected to an impact is considered

with the boundary conditions, whereis the Young's modulus,is the second moment of area,is the bending displacement,is the density,is the cross-sectional area,is the amplitude of the transverse impact load,is the impulse function acting on the positionis the length of the cantilever.
The Preissman Box scheme of the model (Eq. (7)) can be constructed
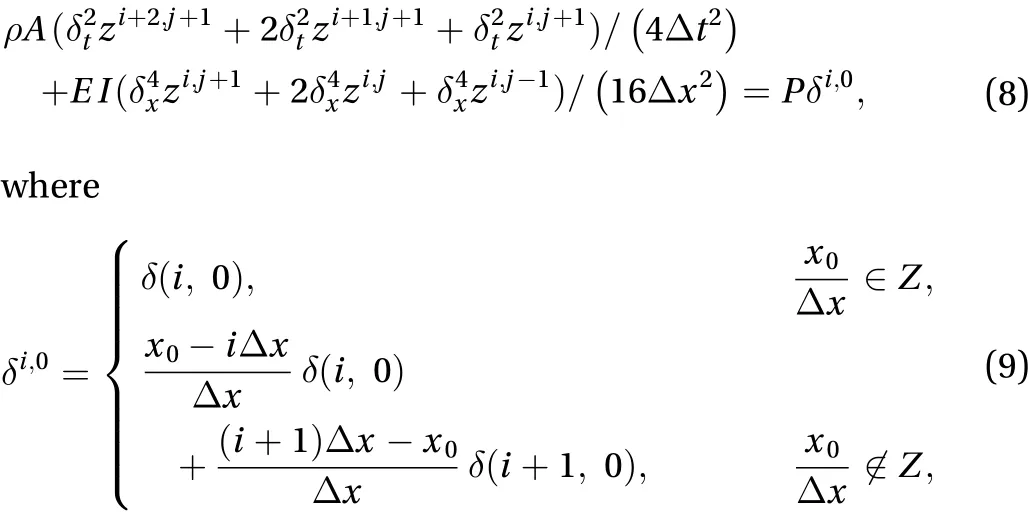
From Table 1, it can be found that the relative errors between numerical simulation results obtained by the scheme (Eq. (8))and those obtained by ABAQUS platform are tiny, which implies that the numerical results obtained employing the scheme(Eq. (8)) is reliable and the structure-preserving method can be used to simulate the non-smooth dynamic system.
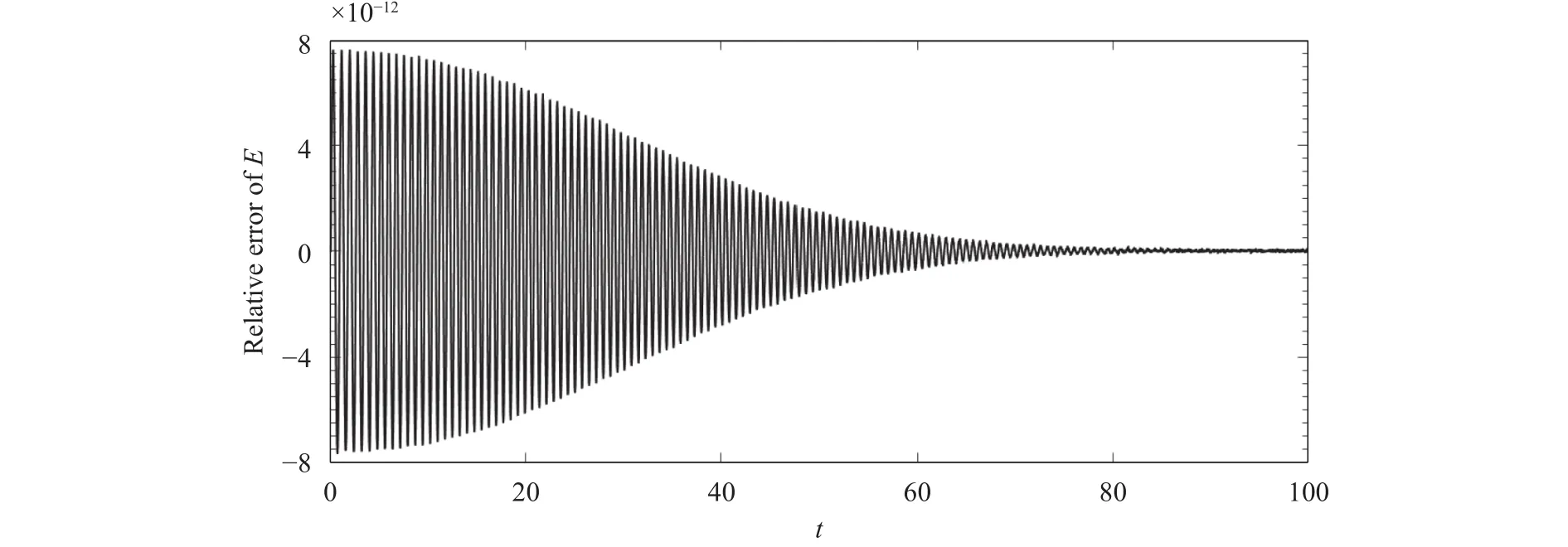
Fig. 1. Relative error of total energy between numerical solution and analytical solution.

Table 1 Relative errors between results obtained by shcheme and those obtained by ABAQUS platform.
As a developing theoretical framework, structure-preserving approach owns some excellent numerical behaviors, such as the well preservation property on the inherit characteristics of the dynamic systems and the significant long-time numerical stability. The current structure-preserving methods mostly focus on the conservative Hamiltonian system, regardless of finite dimensional or infinite dimensional, the reason of which is that the conservations of the system are accompanying with the symmetries of the Hamiltonian equation.
Recently, the generalized multi-symplectic method was proposed for the structure-preserving analysis on the infinite dimensional dynamic systems with the weak damping, which initiates the structure-preserving method for the infinite dimensional nonconservative system. In this letter, the limitation of the generalized multi-symplectic method, i.e., the strict requirement on the weak damping, is broken and the structure-preserving approach is developed for the dynamic systems with the strong excitation. From the numerical results on the two presented examples, it can be concluded that the structure-preserving approach for the infinite dimensional nonconservative system owns excellent longtime numerical behaviors and the high numerical precision.
Acknowledgements
The research was supported by the National Natural Science Foundation of China (Grant 11672241), the Seed Foundation of Qian Xuesen Laboratory of Space Technology, and the Open Foundation of State Key Laboratory of Structural Analysis of Industrial Equipment (Grant GZ1605). The author wishes to thank Prof. Zichen Deng of Northwestern Polytechnical University for several helpful discussions and suggestions.
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Data-driven computing in elasticity via kernel regression
- The effects of mean sea level rise and strengthened winds on extreme sea levels in the Baltic Sea
- New interpretation of specific sign of Reynolds stress in the boundary layer on a flat plate
- An improved smoke-wire flow visualization technique using capacitor as power source
- Head-on collision between two hydroelastic solitary waves with Plotnikov-Toland's plate model
- Linear, nonlinear dynamics, and sensitivity analysis of a vibratory ring gyroscope
