高强钢外伸式端板节点火灾性能试验与数值分析

2018-02-08武念铎罗永峰强旭红

东南大学学报（自然科学版） 2018年1期

武念铎罗永峰强旭红刘晓姜旭

(1同济大学土木工程学院, 上海 200092)(2上海宝冶工程技术有限公司, 上海 200941)

钢材的强度和刚度随温度升高而显著降低,550 ℃ 时,其强度和刚度将降至常温的一半[1],直接影响钢结构火灾时的承载安全性.梁柱端板连接是钢结构广泛采用的连接方式,其火灾下的力学性能对结构整体火灾下的力学性能有显著影响.近年来,高强钢结构在国内外已得到较多应用,故对高强钢端板连接节点火灾下力学性能进行深入研究非常必要且具有重要意义.

针对普通钢端板连接节点火灾下的力学性能,虽然国内外现有研究成果较多[2],但仍不能直接应用于工程实际,故我国和欧洲现行钢结构抗火设计规范[1,3]均未针对端板连接节点给出合理的抗火设计方法,仅以“与邻近构件的最大防火要求相同” 作为节点抗火设计原则.对于高强钢端板连接节点常温下的力学性能,Coelho[4]针对仅端板采用高强钢的齐平式和外伸式端板连接节点的试验研究表明,规范EN 1993-1-8[5]中基于普通钢端板连接节点力学性能提出的计算方法能够较为准确地预测高强钢端板连接节点的承载力,但高估了节点的初始转动刚度,对转动能力的预测也较为保守.孙飞飞等[6]对普通钢、仅端板采用高强钢Q690及端板和柱均采用高强钢Q690的齐平式端板连接节点进行试验研究,得到与Coelho[4]类似的结论,研究亦表明采用高强钢柱会削弱节点的转动能力.Qiang[7]对普通钢和仅端板采用高强钢的齐平式端板连接节点的力学性能进行了试验研究和数值分析,并提出采用薄高强钢端板替代厚普通钢端板的设计理念,但尚未给出具体的设计方法.由于针对高强钢端板连接节点常温下力学性能的研究有限,规范EN 1993-1-8[5]仅在原有普通钢材钢结构设计规范中增加补充条款EN 1993-1-12[8],将规范适用范围推广至S460～S700钢,但该规范仅将高强度结构钢材引入设计规范,而设计方法仍简单套用普通钢的方法,并明确指出目前缺乏高强钢的相关实验和研究依据.对于高强钢端板连接节点火灾下力学性能,仅Qiang[7]对普通钢和仅端板采用高强钢的齐平式端板连接节点的火灾下力学性能进行了试验研究和有限元分析.综上,现阶段针对高强钢端板连接节点火灾下力学性能的研究较少,文献[7]仅对端板采用高强钢的齐平式端板连接节点火灾下力学性能进行研究,而外伸式端板连接节点和齐平式端板连接节点的力学性能、失效模式及设计方法不同,同时文献[6]表明高强钢柱对节点常温下力学行为存在不利影响,故有必要对端板和柱均采用高强钢的外伸式端板连接节点火灾下力学性能进行深入研究.

为此,本文对Q690和Q960高强钢端板连接节点(端板和柱均采用高强钢)进行足尺模型高温550 ℃ 下的试验研究和有限元模拟分析,并将试验结果与采用规范EN 1993-1-8计算的结果进行对比,验证其对于高强钢端板连接节点的适用性.

1 试验

1.1 试件设计

以规范EN 1993-1-8[5]中组件法为理论依据,设计制作了3个高强钢端板连接节点,编号分别为Q690F1,Q960F1,Q960F2.Q690F1的梁、柱和端板均采用Q690钢,梁、柱截面尺寸分别为H300 mm×180 mm×10 mm×12 mm和H340 mm×200 mm×10 mm×12 mm.Q960F1和Q960F2的梁、柱和端板均采用Q960钢,梁、柱截面尺寸分别为H250 mm×180 mm×10 mm×12 mm和H300 mm×200 mm×10 mm×12 mm.试件的端板与梁端均采用12 mm角焊缝连接,端板与柱翼缘均采用10.9 级M27高强螺栓连接.为防止板件局部失稳,梁、柱内设加劲肋.端板上的螺栓布置和编号见图1.

(a) 试件

(b) Q690节点端板

1.2 材料性能

作者前期对S690,S960高强钢高温力学能进行了试验研究,得到其强度和刚度的高温折减系数[9-10].由于常温下S690,S960高强钢分别与Q690,Q960高强钢的力学性能相近、化学成分相似,故本文采用该折减系数乘以通过拉伸试验得到的Q690,Q960高强钢常温下的强度和刚度,获得Q690,Q960高强钢在高温550 ℃ 时的强度和刚度,结果见表1.550 ℃ 时高强螺栓的强度和刚度采用文献[11]中的试验结果(见表1).

表1 550 ℃ 钢材和螺栓力学性能 MPa

1.3 试验装置

试验装置示意图见图2.考虑到火灾条件下对梁施加拉力远比施加压力稳定,故将梁柱节点试件整体倒转放置.火灾试验过程中,试件在炉盖以下部分受火,而炉盖之上部分则处于常温环境.

图2 试验装置示意图

1.4 测点布置

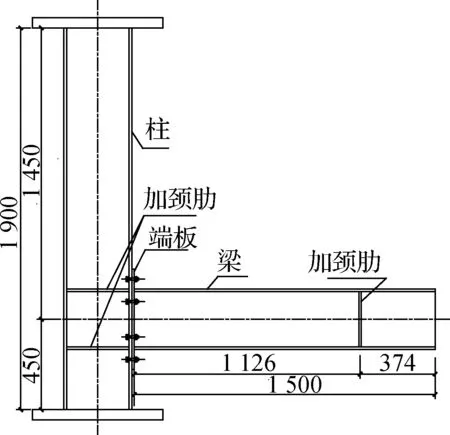
位移计布置示意图见图3.在梁翼缘布置3个竖向位移计DT1,DT2及DT3,测量梁的竖向位移.在柱翼缘布置2个竖向位移计DT4和DT5,测量柱翼缘竖向位移.在节点的端板布置1个竖向位移计DT6,测量端板的竖向位移.在柱翼缘布置2个水平位移计DT7和DT8,测量柱翼缘水平位移.

图3 位移计布置示意图(单位:mm)

1.5 加载制度

经常温下预加载,将仪器设备调试正常后,进行火灾试验.本文采用恒温加载的试验方法,即试件以恒定速率升至目标火灾温度550 ℃ 后对梁端施加荷载,直到试件破坏.升温速率取10 ℃ /min,该值同未保护的建筑结构在真实火灾作用下的升温速度[7]相当.加载期间采用位移控制,速率为 10 mm/min.

2 试验结果与分析

2.1 失效模式

Q690F1和Q960F1的破坏现象分别见图4和图5.由于Q960F1和Q960F2的破坏现象相同，故未列出Q960F2的破坏现象.由图可见，节点破坏后,受拉区的端板和螺栓存在明显的塑性变形,根据EN 1993-1-8[5]可知,节点的失效模式为端板和螺栓组合破坏,即失效模式2.根据EN 1993-1-8中组件法计算分析得到的失效模式也为失效模式2,故该方法可准确预测高强钢端板连接节点550 ℃ 时的失效模式.

(a) 节点

(b) 柱

(d) 端板正视

(e) 螺栓

(a) 节点

(b) 柱

(d) 端板正视

(e) 螺栓

为比较高强钢端板连接节点常温与火灾下力学性能的差异,作者前期对2个Q690和1个Q960高强钢端板连接节点常温下的力学性能进行了试验研究[12],试件编号分别为Q690A1,Q690A2,Q960A1.Q690A1的破坏现象见图6,Q690A2的破坏现象与其相同.Q960A1的破坏现象见图7.由图6和图7可见,节点破坏后,受拉区的端板和螺栓存在明显的塑性变形,根据EN 1993-1-8可知,节点常温下的失效模式为端板和螺栓组合破坏,即失效模式2,故节点常温下与火灾下的失效模式相同.值得注意的是,通过比较节点常温下和火灾下的破坏现象发现,火灾下节点变形更为明显,尤其是受拉区的螺栓,常温下表现为脆性破坏的高强螺栓在火灾下具有很大的拉伸变形能力,颈缩显著,为延性破坏.

(a) 节点

(b) 柱

(d) 端板正视

(e) 螺栓

(a) 节点

(b) 柱

(d) 端板正视

(e) 螺栓

2.2 弯矩-转角曲线

梁柱节点的力学性能一般采用M-θ曲线描述,其中M为节点所承受的弯矩,θ为节点转角,其计算公式分别为

M=PLload

(1)

θ=θb-θc

(2)

式中,P为荷载;Lload为荷载施加点至端板中面的距离;θb,θc分别为梁、柱转角.

θb的计算公式为

(3)

(4)

式中,δDTi为位移计DTi测得的位移;δbel,DTi为梁在DTi处的弹性位移;Eb为梁钢材的弹性模量;Ib为梁截面惯性矩;xDTi为位移计DTi距端板中面的距离.

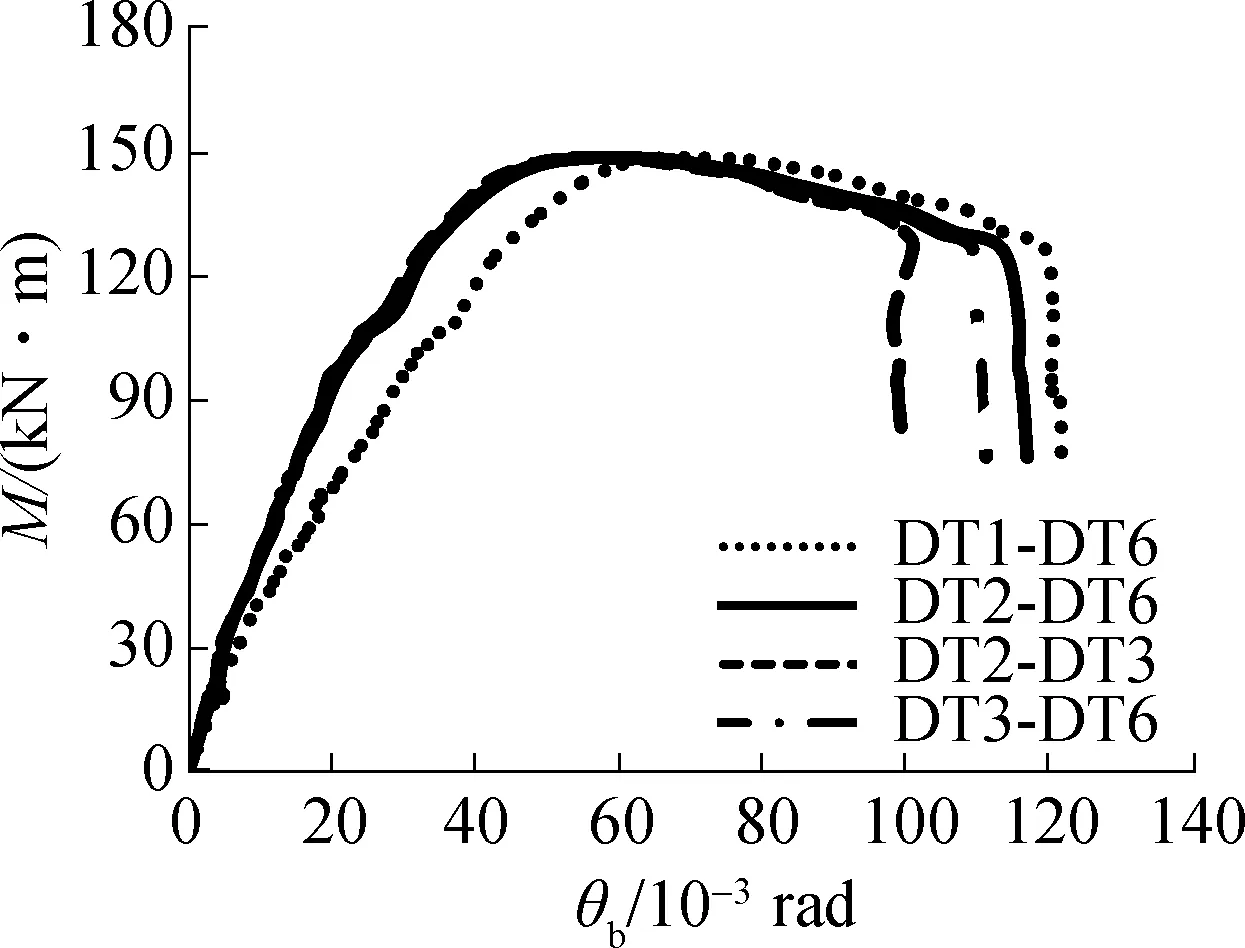
节点的M-θb曲线见图8.图中,曲线DTi-DTj表示通过位移计DTi和DTj测量得到的计算结果.由于试验中试件Q690F1和Q960F2的位移计DT3发生故障,未能采集到DT3的数据,故图8中并未列出二者采用DT3计算得到的M-θb曲线.

(a) Q690F1

(b) Q960F1

由图8(b)可见,曲线DT2-DT6,DT2-DT3及DT3-DT6基本一致,仅在曲线末端(即垂直下降段起点)有所偏差;曲线DT1-DT6与其他曲线偏差较大.在曲线末端,节点受力状态受材料性能、荷载偏心、加载设备应变能释放等因素影响,极不稳定,故各位移计在该点附近的测量值有所偏差,导致曲线DT2-DT6,DT2-DT3及DT3-DT6在垂直下降段的起点有所偏差.由于DT1靠近端板,在该区域式(4)不适用,故采用DT1和DT6的测量值计算θb时存在较大偏差.因此,后续分析中,θb采用DT2和DT6测量值的计算结果.

θc的计算公式为

(5)

(6)

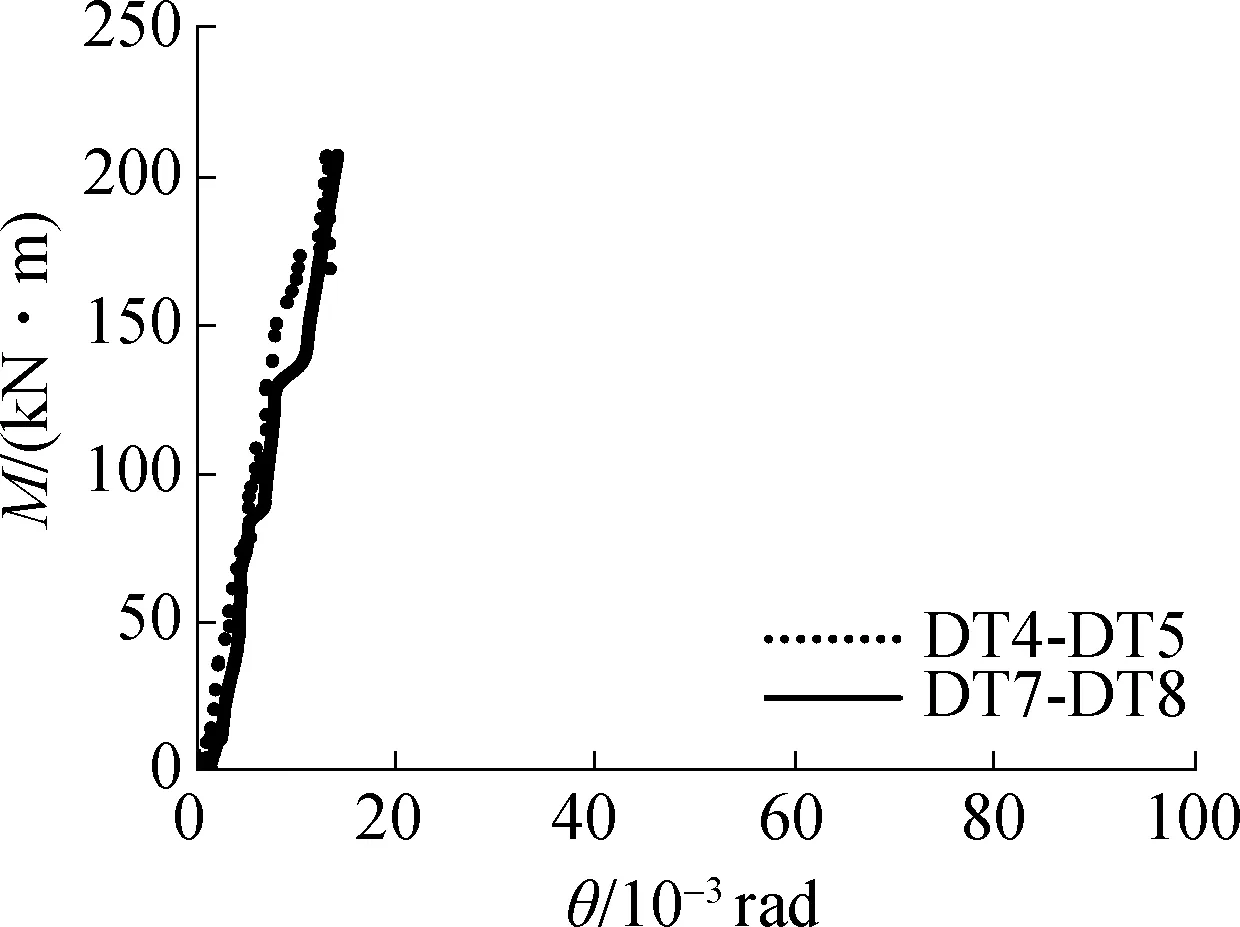
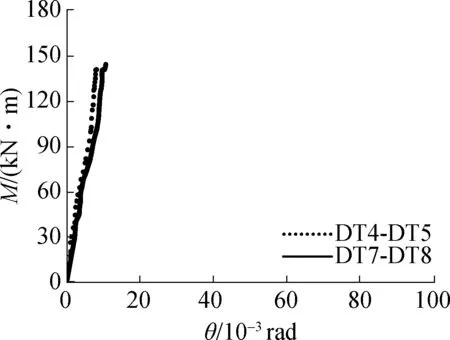
节点的M-θc曲线见图9.由图可见,各组数据吻合良好,后续分析中,θc采用DT4-DT5测量值的计算结果.由式(2)求得试件的转角θ,并绘出节点的M-θ曲线.图10为常温和火灾下试件的M-θ

(a) Q690F1

(b) Q960F1

曲线[12].依据此曲线,可得节点主要力学指标的试验值,包括初始转动刚度Kini、受弯承载力My、受弯承载力对应的转角θy、极限弯矩Mmax、极限弯矩对应的转角θmax,C点对应的横坐标值和极限转角Φc(见图11).

(a) Q690

(b) Q960

图11 节点主要力学指标

2.3 受弯承载力

本文采用EN 1993-1-8规范中建议的方法确定节点的受弯承载力试验值My,exp,根据组件法计算得到受弯承载力的理论值My,EC3.表2中列出了My,exp,My,EC3及二者比值.由表可见,节点的My,exp略大于My,EC3,但基本一致,故EN 1993-1-8规范中的组件法可较为准确地预测高强钢端板连接节点高温550 ℃ 下的承载力.

表3列出了试验得到的高温、常温[12]下节点的承载力平均值,二者比值即为节点高温下的承载力折减系数.550 ℃ 时,Q690和Q960高强钢端板连接节点的承载力分别为常温时的45%和46%.

表2 节点受弯承载力 kN·m

表3 节点承载力平均值和承载力折减系数

2.4 初始转动刚度

根据节点的M-θ曲线,得到初始转动刚度试验值Kini,exp, 按照EN 1993-1-8规范中的组件法计算得到节点的转动刚度理论值Kini,EC3.表4列出了Kini,exp,Kini,EC3及二者比值.由表可见,节点的初始转动刚度理论值均大于试验值.导致计算结果偏高的原因在于:① 组件法是在普通钢研究成果上提出的,本文研究的节点是高强钢,超出其建议的适用范围;② 节点域火灾温度场分布不均匀,导致火灾下节点域各处的材料力学性能有偏差;③ 组件法在计算节点初始转动刚度时忽略梁翼缘的抗拉刚度,本文试件则均采用高强钢,故梁截面尺寸较小,梁翼缘抗拉刚度不可忽略.

表4 节点初始转动刚度 kN·m/rad

表5列出试验得到的高温、常温[12]下节点的初始转动刚度平均值,二者比值即为节点高温下的初始转动刚度折减系数.由表可见,550 ℃ 时Q690和Q960高强钢端板连接节点的初始转动刚度分别为常温时的57%和65%.

表5 节点初始转动刚度平均值和初始转动刚度折减系数

2.5 转动能力

对于普通钢端板连接节点,文献[4]建议:Φc达到0.04～0.05 rad即可认为其具有足够的转动能力.Wilkinson等[13]认为,节点的塑性转角θp>0.03 rad时,在地震作用下节点不会先于构件破坏.其中,θp的计算公式为

θp=Φc-θe

(7)

(8)

EN 1993-1-8规范建议:若节点的受弯承载力由端板或柱翼缘控制,且柱翼缘或端板厚度t满足

(9)

则节点的转动能力满足要求.

对节点的M-θ曲线进行分析,并结合式(7)和(9),得到节点的Φc和θp(见表6).由表可知,Φc>0.05 rad,θp>0.03 rad,因此可认为节点的转动能力良好.

表6 节点转角 10-3 rad

根据EN 1993-1-8规范中关于保障节点转动能力的相关要求,Q690和Q960高强钢端板连接节点火灾下具备良好转动能力的前提分别是端板厚度t≤8.63 mm和t≤7.07 mm.本文试验结果表明,虽然节点的端板厚度12 mm超过EN 1993-1-8规范中的上限值,但节点的转动能力良好,故采用EN 1993-1-8规范中的相关要求对高强钢端板连接节点进行抗火设计偏于保守.

表7为试验得到的高温、常温[12]下节点的转动能力平均值,二者比值即为节点高温下的转动能力提高系数.由表可见,550 ℃ 时,Q690高强钢端板连接节点的转动能力为常温时的1.43倍,Q960则为1.66倍.

表7 节点转动能力平均值和转动能力提高系数

3 有限元数值分析

3.1 有限元模型

本文采用ABAQUS软件建立有限元模型.由于试件的几何尺寸、荷载及边界条件具有对称性,为节约计算时间,取1/2试件进行建模分析.节点的有限元模型见图12,模型采用八节点六面体线性减缩积分单元C3D8R.

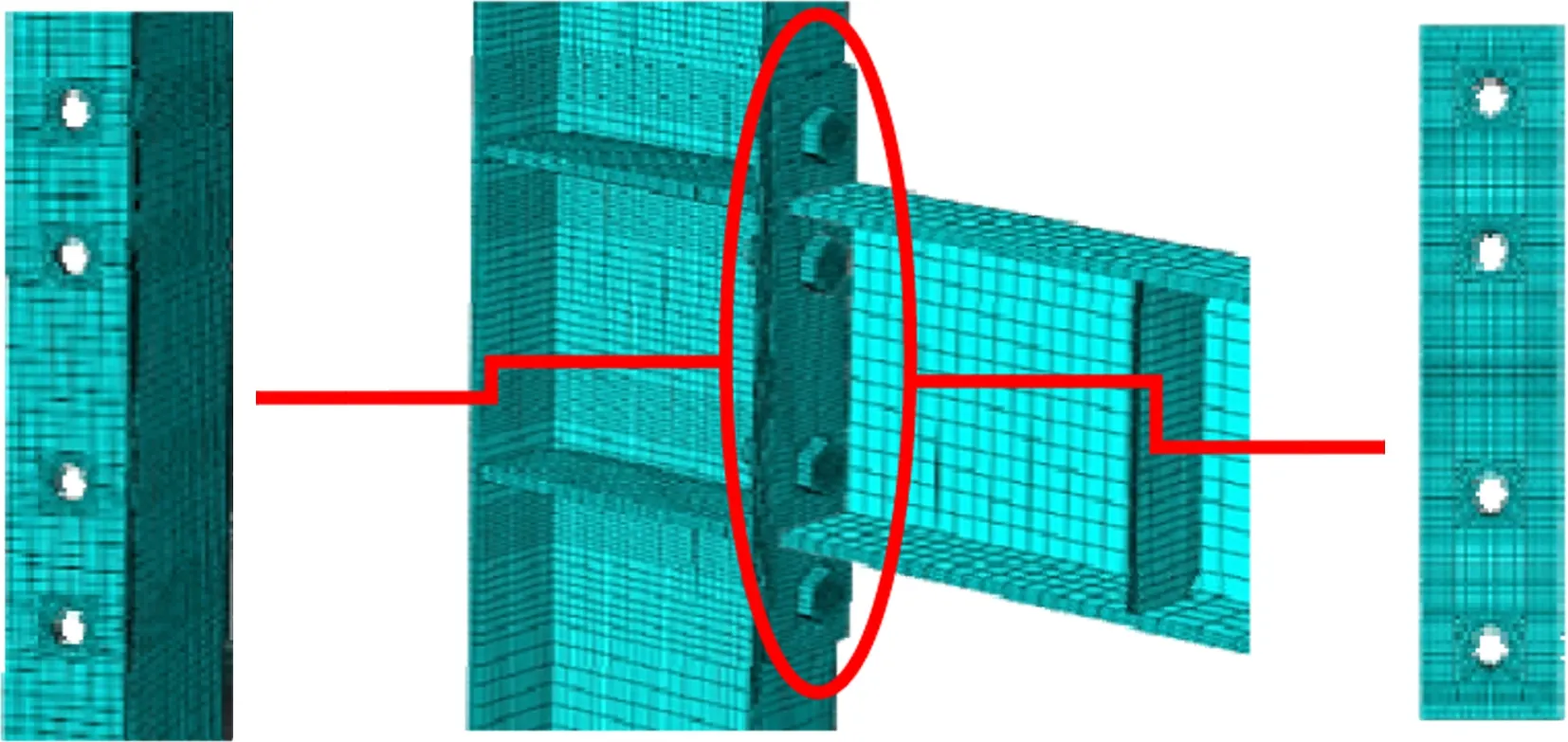
图12 网格划分

模型中的接触部件包括螺帽柱翼缘、螺杆螺孔、螺杆螺母、螺母端板及柱翼缘端板.接触对中面面接触的属性采用有限滑移.螺杆与螺母采用绑定约束模拟.为解决接触分析的收敛问题,分析过程包括以下5步:① 临时约束螺栓和端板的所有自由度,施加10 N的螺栓预紧力;② 释放螺栓和端板的临时约束;③ 固定螺栓长度;④ 将温度场设为550 ℃;⑤ 施加荷载进行计算.其中,步骤①～③用以保证接触关系的平稳建立,可有效解决接触分析的收敛问题[7].数值计算时考虑材料与几何双重非线性效应,节点各组件的失效准则采用文献[7]中的建议.

根据EN 1993-1-2[1]规范给出的考虑材料强化的应力应变关系,建立高强钢和高强螺栓的应力应变本构关系.本构关系中,材料的真实应力σtrue和真实应变εtrue分别为

εtrue=ln(1+εeng)

(10)

σtrue=σeng(1+εeng)

(11)

式中,σeng,εeng分别为材料的工程应力和应变,依据表1中的试验结果确定.文献[14]表明,采用上述方法模拟材料本构关系的有限元模型可准确模拟节点火灾下的力学性能.

3.2 有限元分析结果

3.2.1 失效模式

有限元模拟得到的各试件破坏形态与试验结果较为吻合.试验所得Q690F1的破坏形态与有限元模拟结果的对比图见图13.有限元模拟得到Q690F1的端板和螺栓的等效塑性应变云图与试验所得破坏形态的对比分别见图14和15,由图可见,二者较为吻合.

(a) 应力云图

(b) 试验

3.2.2 M-θ曲线

试验和有限元模拟得到的各节点的M-θ曲线见图16.由图可见,除下降段外,试验结果与有限元模拟结果吻合良好.由于有限元模型求解时采用完全牛顿法,无法模拟M-θ曲线的下降阶段,故无法得到Φc.

(a) 等效塑性应变云图

(b) 试验

(a) 螺栓1-1等效塑性应变云图

(b) 螺栓1-1试验结果

(d) 螺栓2-1试验结果

(a) Q690

(b) Q960

试验所得的节点极限承载力Mmax,exp、有限元模拟所得节点极限承载力Mmax,FEM及二者比值见表8.由表可见,二者最大偏差为7%.

表8 节点极限承载力对比 kN·m

综上,本文建立的有限元模型可较为合理、准确地模拟高强钢端板连接节点高温550 ℃ 下的力学行为.

4 结论

1) 高强钢端板连接节点高温550 ℃ 下的失效模式与常温时相同,均为端板和螺栓组合破坏,为延性破坏.但常温下为脆性破坏的高强螺栓在550 ℃ 下具有很大的拉伸变形能力、颈缩显著,为延性破坏.

2) 550 ℃ 时,Q690和Q960高强钢端板连接节点的承载力分别为常温时的45%和46%,初始转动刚度为常温时的57%和65%,但转动能力分别为常温时的1.43倍和1.66倍.

3) EN 1993-1-8规范中针对普通钢端板节点失效模式和节点受弯承载力的预测方法可直接用于预测高强钢端板连接节点550 ℃ 时的失效模式和受弯承载力,但针对普通钢端板节点初始转动刚度的预测方法高估了高强钢端板连接节点550 ℃ 时的初始转动刚度.550 ℃ 时,采用EN 1993-1-8规范中关于保障节点转动能力的相关要求对高强钢端板连接节点进行抗火设计偏于保守.

4) 有限元模型能准确模拟节点的失效模式和M-θ曲线,可作为后续参数分析的依据.

)

[1] European Committee for Standardization. EN 1993-1-2 Eurocode 3—Design of steel structures—Part 1-2: General rules-structural fire design [S]. Brussels: CEN, 2005: 45-46.

[2] Al-Jabri K S. Modelling and simulation of beam-to-column joints at elevated temperature: A review [J].JournaloftheFranklinInstitute, 2011,348(7):1695-1716. DOI:10.1016/j.jfranklin.2010.09.002.

[3] CECS 200:2006. 建筑钢结构防火技术规范[S]. 北京: 中国计划出版社,2006.

[4] Coelho A M G. Characterization of the bolted endplate beam-to-column steel connections [D]. Coimbra, Portugal: School of Structural Engineering of University of Coimbra, 2004.

[5] European Committee for Standardization. EN 1993-1-8 Eurocode 3—Design of steel structures—Part 1-8: Design of joints [S]. Brussels: CEN, 2005.

[6] 孙飞飞, 孙密,李国强, 等. Q690高强钢端板连接梁柱节点抗震性能试验研究[J]. 建筑结构学报, 2014, 35(4): 116-124.

Sun Feifei, Sun Mi, Li Guoqiang, et al. Experimental study on seismic behavior of high-strength steel beam-to-column end-plate connections [J].JournalofBuildingStructures, 2014,35(4): 116-124.(in Chinese)

[7] Qiang X. Behavior of high strength steel endplate connections in fire and after fire [D]. Delft: School of Civil Engineering and Geosciences of Delft University of Technology, 2013.

[8] European Committee for Standardization. EN 1993-1-12 Eurocode 3—Design of steel structures—Part 1-12: Additional rules for the extension of EN 1993 up to steel grade S700 [S]. Brussels:CEN, 2007.

[9] Qiang X, Bijlaard F S K, Kolstein H. Post-fire mechanical properties of high strength structural steels S460 and S690[J].EngineeringStructures, 2012,35: 1-10. DOI:10.1016/j.engstruct.2011.11.005.

[10] Qiang X, Bijlaard F S K, Kolstein H. Post-fire performance of very high strength steel S960[J].JournalofConstructionalSteelResearch, 2013,80: 235-242. DOI:10.1016/j.jcsr.2012.09.002.

[11] 李国强, 李明菲, 殷颖智, 等. 高温下高强度螺栓20MnTiB钢的材料性能试验研究[J]. 土木工程学报, 2001, 34(5): 100-104. DOI:10.3321/j.issn:1000-131X.2001.05.020.

Li Guoqiang, Li Mingfei, Yin Yingzhi, et al. Experimental studies on the behavior of high-strength bolts made of 20MnTiB steel at elevated temperatures[J].ChinaCivilEngineeringJournal, 2001,34(5): 100-104. DOI:10.3321/j.issn:1000-131X.2001.05.020.(in Chinese)

[12] 强旭红, 武念铎, 罗永峰, 等. 全高强钢端板节点火灾后性能试验[J]. 同济大学学报(自然科学版), 2017, 45(2): 173-179,194. DOI:10.11908/j.issn.0253-374x.2017.02.003.

Qiang Xuhong, Wu Nianduo, Luo Yongfeng, et al. Experimental research on post-fire behavior of full high strength steel endplate connections[J].JournalofTongjiUniversity(NaturalScience), 2017,45(2): 173-179,194. DOI:10.11908/j.issn.0253-374x.2017.02.003.(in Chinese)

[13] Wilkinson S, Hurdman G, Crowther A. A moment resisting connection for earthquake resistant structures[J].JournalofConstructionalSteelResearch, 2006,62(3): 295-302. DOI:10.1016/j.jcsr.2005.07.011.

[14] Gao Y, Yu H, Shi G. Resistance of flush endplate connections under tension and shear in fire[J].JournalofConstructionalSteelResearch, 2013,86: 195-205. DOI:10.1016/j.jcsr.2013.03.015.