基于FEM-DMF的耦合损耗因子预示精度分析

王 攀 陈 强 戴元伦 费庆国 张 鹏 李彦斌

(1东南大学土木工程学院, 南京 210096)(2东南大学空天机械动力学研究所, 南京 211189)(3中国船舶重工集团公司第701研究所, 武汉 430064)(4东南大学机械工程学院, 南京 211189)

统计能量分析[1](statistical energy analysis, SEA)能够很好地描述系统各组件的平均振动特性,是目前解决高频环境中复杂结构动力学问题的有效方法,已成功应用于航空航天、汽车、船舶等领域[2-4].应用统计能量分析对复杂结构进行高频动响应预示时,其重点在于确定统计能量分析参数[5],即子系统的模态密度、子系统的内损耗因子、子系统之间的耦合损耗因子.其中,耦合损耗因子表征子系统间的能量传递效率,是统计能量分析中的关键参数,其准确的获取直接影响到结构振动能量的预示精度.

目前,获取耦合损耗因子的常用方法有试验方法、波方法[6](wave method)、功率输入法(power injection method, PIM)等.对于部分工程实际结构,其耦合损耗因子常采用试验来获取,然而试验分析具有耗费大、试验条件与试验工况有限等缺点.波方法是获取耦合损耗因子的传统方法之一,但该方法仅适用于简单结构,如耦合梁、L型耦合板、T型耦合板等[7],对于复杂结构无法给出相应的理论解.PIM是获取结构耦合损耗因子的经典方法之一,国内外许多学者均对PIM开展了相关的研究.Mace等[8]通过有限元(finite element method,FEM)获取了系统的模态、质量矩阵和刚度矩阵,进而计算子系统的输入功率和振动能量,并结合PIM得到了能量影响系数矩阵中的各项参数;Bies等[9]利用PIM预示了2个板耦合结构的损耗因子矩阵;Lalor[10]对PIM进行了改进,将损耗因子矩阵分开求解,使得计算更加简便而且在一定程度上提高了预示精度;张鹏等[11]利用PIM研究了材料物性热效应对统计能量分析参数的影响;陈强等[12]基于FEM-PIM给出了一种热环境下适用于复杂结构的统计能量分析方法,并研究了热效应对统计能量分析参数的影响.目前,基于FEM-PIM预示的耦合损耗因子具有较高的精度,但采用该方法预示复杂结构耦合损耗因子时,需要利用结构的整体模态和所有节点的振型计算输入功率和振动能量,计算效率较低;且随着结构子系统数量的增加,损耗因子矩阵容易出现病态,计算稳定性较差.

双模态方程法(dual modal formulation, DMF)利用耦合边的模态阵型和子系统的其他模态参数,直接计算得到子系统间的耦合损耗因子,节省大量的计算时间,提高了计算效率;此外,对于结构阻尼不同的子系统,DMF方法也可以预示其子系统间的耦合损耗因子.Maxit等[13]通过对子系统解耦分析,利用DMF方法计算了耦合梁结构的耦合损耗因子;孔宪仁等[14]利用DMF方法估计了铝蜂窝夹层结构的耦合损耗因子.目前针对DMF方法的相关研究误差较大,较难应用于实际工程.

因此,本文基于FEM-DMF方法开展结构耦合损耗因子的预示精度及适用范围研究.以典型L型耦合板为研究对象,通过与FEM-PIM对比,深入研究了分析频带、子系统刚度比和结构阻尼对FEM-DMF方法预示耦合损耗因子精度的影响.以L型耦合加筋板为研究对象,验证了FEM-DMF方法在复杂结构中的适用性.

1 基于FEM-DMF的耦合损耗因子预示理论

DMF理论最初由Maxit等[15]提出,该方法用虚构的边界将系统切割成如图1所示的连续耦合的子系统,并对子系统在耦合边界上的边界条件进行近似;对于较“刚”子系统,假定其在耦合边界上处于自由状态,对于较“柔”子系统,假定其在耦合边界上处于固支状态;用位移模态描述较“刚”子系统,用应力模态描述较“柔”子系统.子系统1和子系统2间的模态功率流平衡方程可以写成类似于SEA功率平衡方程的形式,即

(1)

(2)

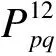
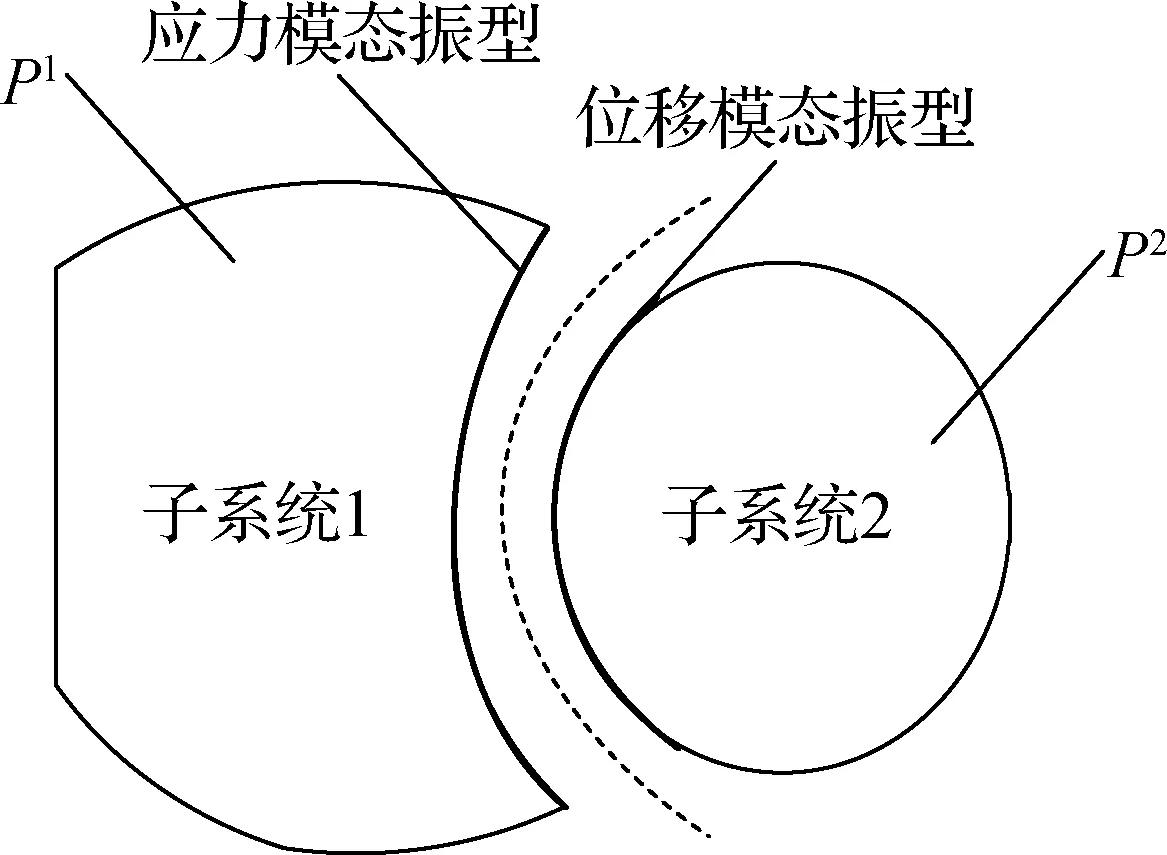
图1 连续耦合子系统示意图

模态耦合损耗因子可以通过子系统解耦后的模态来获得,其表达式为

(3)

(4)

通过结合有限元分析方法,子系统之间的耦合边界会被离散成若干节点.对于L型耦合板,依据DMF理论将其分为板1和板2,分析2个板的有限元模态振型,每个节点具有6个自由度,但在弯曲情况下,只有节点力第5个自由度(沿耦合边方向的弯矩)和节点位移第5个自由度是不为零.故板1的p模态和板2的q模态之间相互作用的计算式被简化为

(5)

子系统之间的模态功率流P12为所有单个模态之间功率流的总和,即

(6)

式中,N1和N2为频率带宽内的共振模态阶数.

假设任意子系统中,在模态阶数大于5的频段内所有共振模态的振动能量相等[16],即

(7)

(8)

将式(6)、(7)和(8)联立,得

(9)

式中,η12为子系统1对子系统2的耦合损耗因子,其表达式为

(10)

式中,ωc为1/3倍频程中心频率.

本文应用NASTRAN对各子系统进行模态分析,获取固有频率和模态振型;并基于FEM-DMF方法的理论,采用MATLAB编程实现结构耦合损耗因子预示的数值计算过程.

2 算例

首先,以L型耦合板为研究对象,分别研究了分析频带、子系统刚度比和结构阻尼对耦合损耗因子预示精度的影响;随后,以L型耦合加筋板为研究对象,研究了FEM-DMF方法在复杂结构耦合损耗因子预示中的适用性.为方便对比计算效率,本文所有计算均在同一台计算机上进行,其配置为英特尔酷睿i7-4770K处理器、内存32GB的台式电脑,Windows 7(64位)系统.

2.1 分析频带对耦合损耗因子预示精度影响

由于耦合损耗因子的预示理论中存在着模态能量均一化假设,故需要对基于FEM-DMF方法预示耦合损耗因子的有效频率范围进行研究.

L型耦合板几何模型如图2所示.板1和板2的材料属性均为:弹性模量E=200 GPa,密度ρ=7 800 kg/m3,泊松比v=0.3,阻尼损耗因子η=0.02.由于薄壁结构主要以弯曲模态为主,因此采用2D板单元建立其有限元模型,单元尺寸为10 mm.结构中的非耦合边简支,耦合边为自由状态.

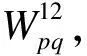
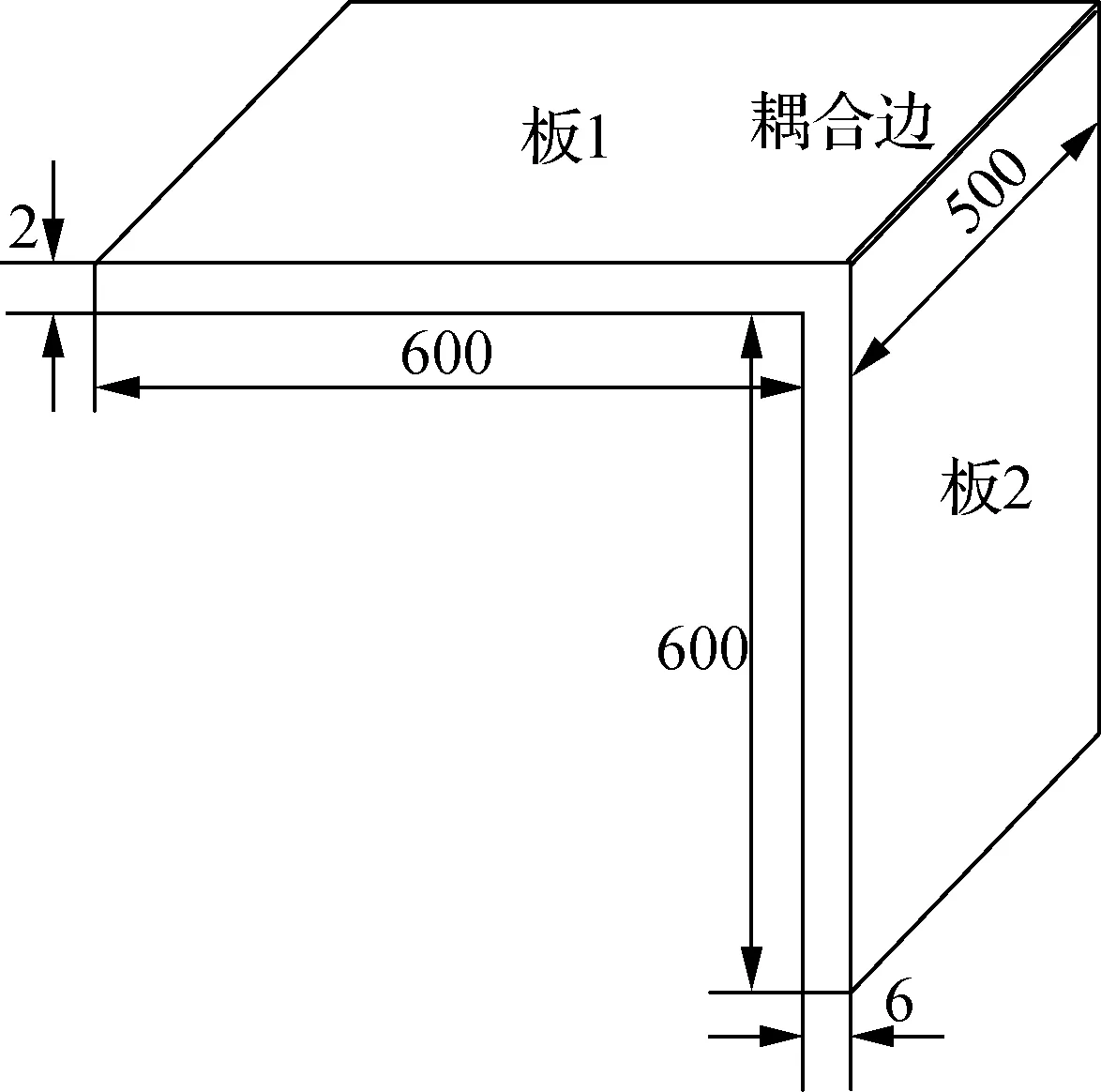
图2 L型耦合板(单位:mm)

为了满足模态能量均一化假设[16],即子系统在1/3倍频程频带内的模态阶数需大于5,对各子系统的模态进行分析,1/3倍频程频带内板1和板2的模态阶数如图3所示,虚线为板1和板2在研究频带内模态阶数均大于5的最低频率.由图3可知,在1.6 kHz以上各子系统的模态阶数均大于5,满足模态能量均一化假设,因此由FEM-DMF方法预示该耦合板的耦合损耗因子在1.6 kHz以上更接近真实值.

图3 1/3倍频程频带内板1和板2的模态数

将FEM-DMF方法预示的耦合损耗因子与采用FEM-PIM所得结果进行对比分析,如图4所示.分析可知,2种方法计算得到的耦合损耗因子变化趋势基本一致,耦合损耗因子均随着频率的升高而逐渐减小;在低于1.25 kHz的频段内,基于FEM-DMF方法计算得到的耦合损耗因子误差较大,这主要是由于L型耦合板在分析频段内模态阶数小于5,难以满足模态能量均一化假设.大于1.6 kHz的频段,2种方法的计算结果基本一致,且最大误差不超过1 dB,这说明对于上述L型耦合板结构,

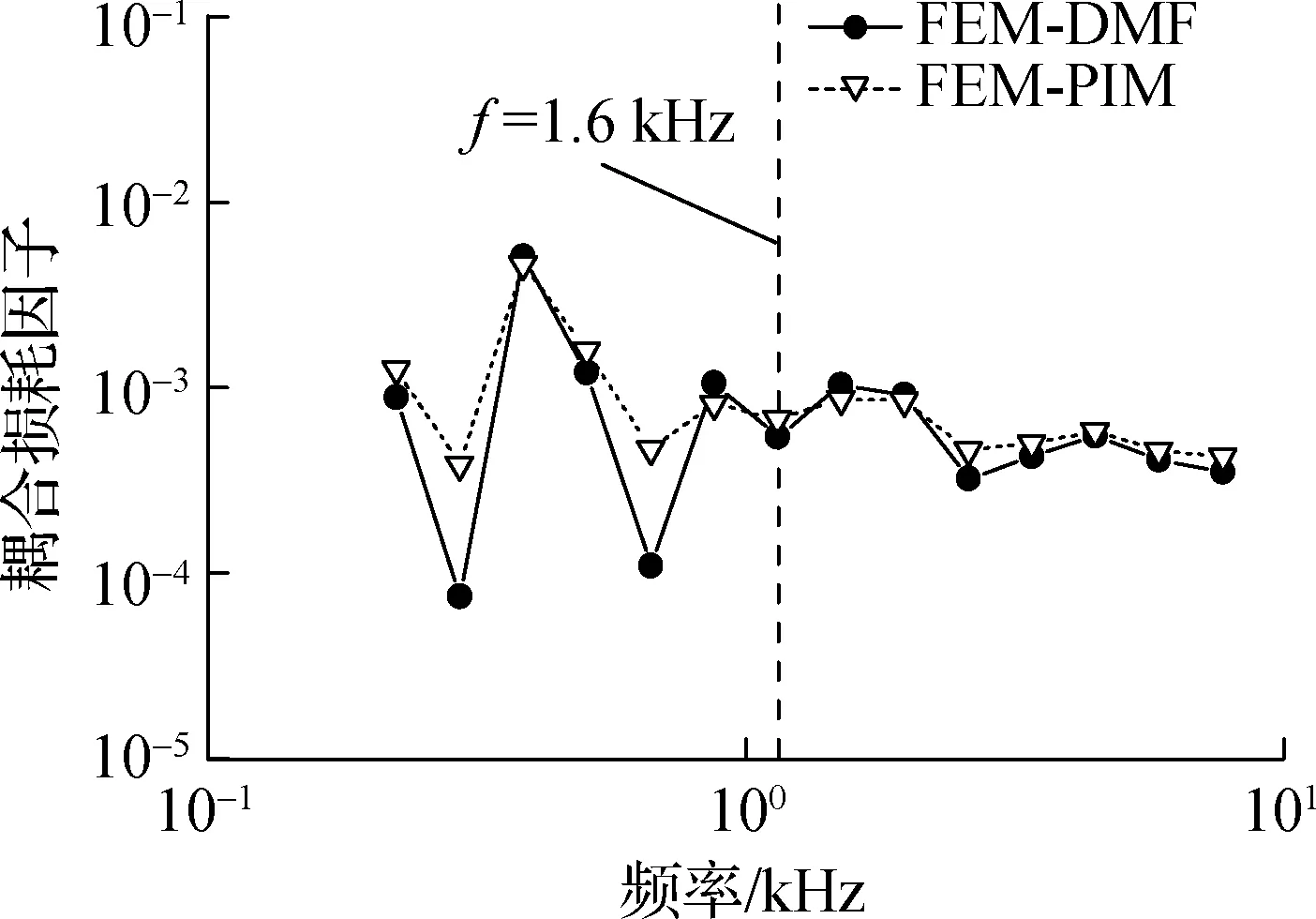
图4 耦合损耗因子

FEM-DMF方法能够较好地保证结构耦合损耗因子的预示精度.从计算效率方面看,FEM-DMF方法的运行程序时间约为15 min,而FEM-PIM需要约1.5 h,因而FEM-DMF方法具有更高的计算效率.

2.2 刚度比对耦合损耗因子预示精度影响

FEM-DMF方法是用虚构的边界将系统切割成连续耦合的子系统,并对子系统在耦合边上的边界条件进行近似;对于较“刚”子系统,假定其在耦合边界上处于自由状态;对于较“柔”子系统,假定其在耦合边界上处于固支状态.当L型耦合板子系统刚度比改变时,子系统在耦合边上的边界条件近似精度随之变化,进而影响耦合损耗因子的预示精度.因此,有必要研究子系统刚度比对耦合损耗因子预示精度的影响.

由于耦合板的材料属性相同,因此子系统的弯曲刚度比与板厚度比的3次方成正比,本文采用2个板厚度比(h2/h1)来表征子系统刚度比的变化,定义板1和板2的厚度分别为h1和h2,其中板1厚度h1=2 mm.计算子系统刚度比为1.0,3.4,8.0,27.0(板2厚度h2为2,3,4,6 mm)时L型耦合板的耦合损耗因子.由2.1节可知,FEM-PIM考虑了结构间的强耦合作用,其预示结果具有较高的精度,因此可采用FEM-PIM验证FEM-DMF方法预示结果的准确性.FEM-PIM和FEM-DMF方法的计算结果如图5所示,其中，虚线为板1和板2在频带内模态阶数均大于5的最低频率.

分析可知,随着刚度比增大,由FEM-DMF方法预示的耦合损耗因子逐渐接近FEM-PIM的耦合损耗因子.由此可知,刚度比的变化对FEM-DMF方法预测结果的准确性有较大影响,随着刚度比的增大预示结果更加准确.

为了更加直观地给出预示精度的临界值,本文计算多组刚度比下耦合板的耦合损耗因子,图6为中心频率为4 000和6 350 Hz频段内结构耦合损耗因子随着刚度比的变化曲线.分析可知,当刚度比小于8.0时,基于FEM-DMF方法计算得到的耦合损耗因子与FEM-PIM的耦合损耗因子相差较大.这主要是由于FEM-DMF方法是利用解耦后的子系统模态去描述其振动特性,当2个子系统刚度比接近1时,子系统间的刚度差异无法用位移和应力模态阵型去描述.而当刚度比大于8.0时,由FEM-DMF方法预示的耦合损耗因子与FEM-PIM的耦合损耗因子基本吻合.因此,刚度比越大,基于FEM-DMF方法的耦合损耗因子预示精度越高.

(b) 刚度比为3.4

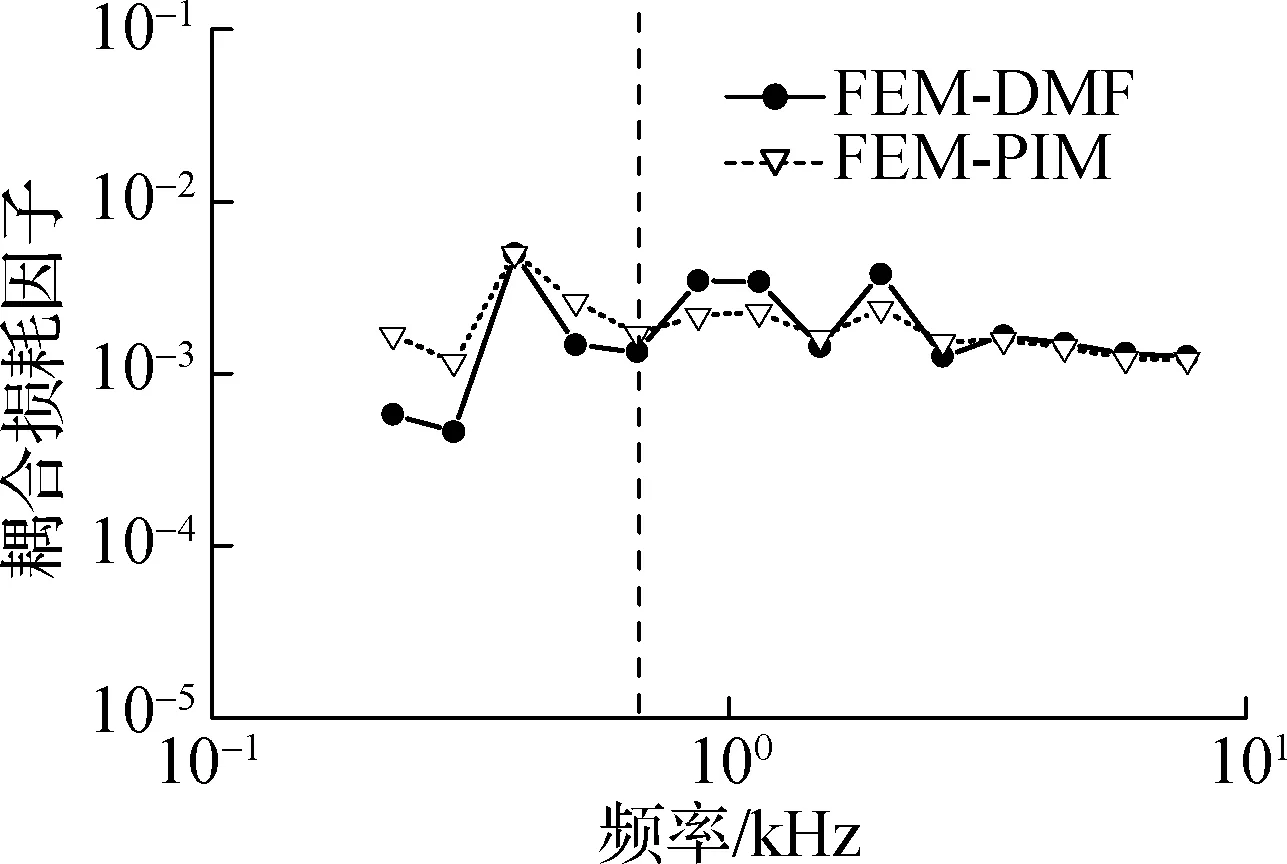
(c) 刚度比为8.0

(d) 刚度比为27.0

2.3 结构阻尼对耦合损耗因子预示精度影响

在实际工程中,不同结构通常具有不同的结构阻尼,为研究结构阻尼对耦合损耗因子预示精度的影响,开展L型耦合板在不同结构阻尼下的耦合损耗因子预示研究.图7(a)、图6(a)和图7(b)分别给出了结构阻尼为0.03,0.02和0.01时3 564～4 490 Hz频带(中心频率为4 000 Hz)内结构的耦合损耗因子,并利用FEM-PIM结果进行验证.为方便讨论分析,当FEM-DMF方法预示的耦合损耗因子与FEM-PIM的耦合损耗因子之间误差小于1 dB时,定义此时的刚度比δc为满足耦合损耗因子预示精度的临界刚度比.

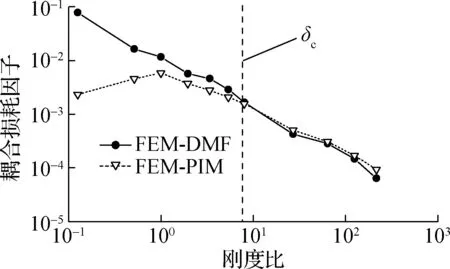
(a) 中心频率为4 000 Hz

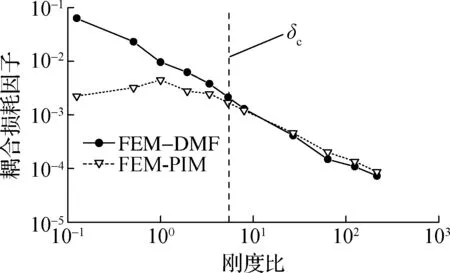
(b) 中心频率为6 350 Hz

(a) 结构阻尼为0.03

(b) 结构阻尼为0.01

图7不同结构阻尼下结构耦合损耗因子随刚度比的变化

计算结果表明:当结构阻尼为0.03时,临界刚度比为3;当结构阻尼为0.02时,临界刚度比为8;当结构阻尼为0.01时,临界刚度比为9.由此可见,在结构刚度比相同的条件下,FEM-DMF方法的预示精度随耦合板结构阻尼的增大而提高.

为更直观地给出L型耦合板的结构阻尼与临界刚度比之间的关系,计算结构阻尼分别为0.002,0.005,0.008,0.01,0.02,0.03的临界刚度比,计算结果如图8所示.分析可知,随着L型耦合板阻尼的增大,满足耦合损耗因子预示精度的临界刚度比减小.经典的波方法假设,当阻尼损耗因子相对于耦合损耗因子足够大时,阻尼损耗因子对耦合损耗因子的影响不大.当结构阻尼大于0.01时,结构阻尼与临界刚度比之间的关系曲线趋于平缓.结合图7(a)、图6(a)和图7(b)可以看出,若结构阻尼较大时,结构阻尼的改变对耦合损耗因子的影响较小,且主要发生在刚度比较小范围,在刚度比较大时对预示精度影响不大.

图8 结构阻尼与临界刚度比之间的关系曲线

2.4 复杂结构耦合损耗因子预示

为验证FEM-DMF方法在复杂结构中的适用性,以L型耦合加筋板(2个板夹角为90°)为研究对象,其几何模型如图9所示,利用FEM-DMF方法预示其耦合损耗因子.仅对厚度较薄的板1进行加筋处理,加筋方式为横纵交错,垂直耦合边方向筋条间距和平行耦合边方向筋条间距均为0.1 m.板1和板2的材料属性与2.1节L型耦合板相同,筋条材料参数与平板一致,筋条宽度为0.01 m，厚度为2 mm.

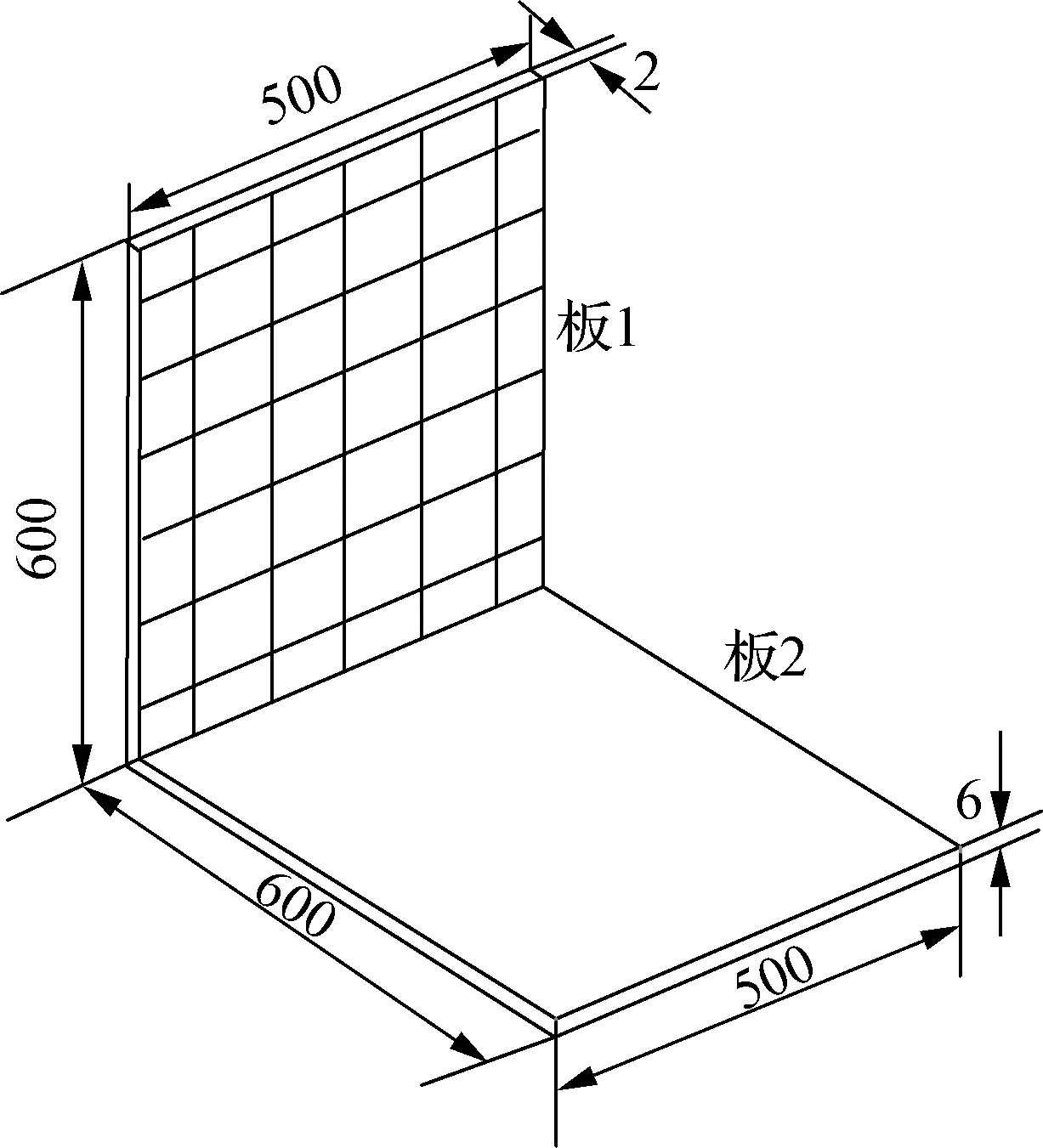
图9 L型耦合加筋板(单位:mm)

利用FEM-PIM对FEM-DMF方法预示的耦合损耗因子进行验证和分析,计算结果如图10所示,其中虚线为板1和板2在研究频带内模态阶数均大于5的最低频率.

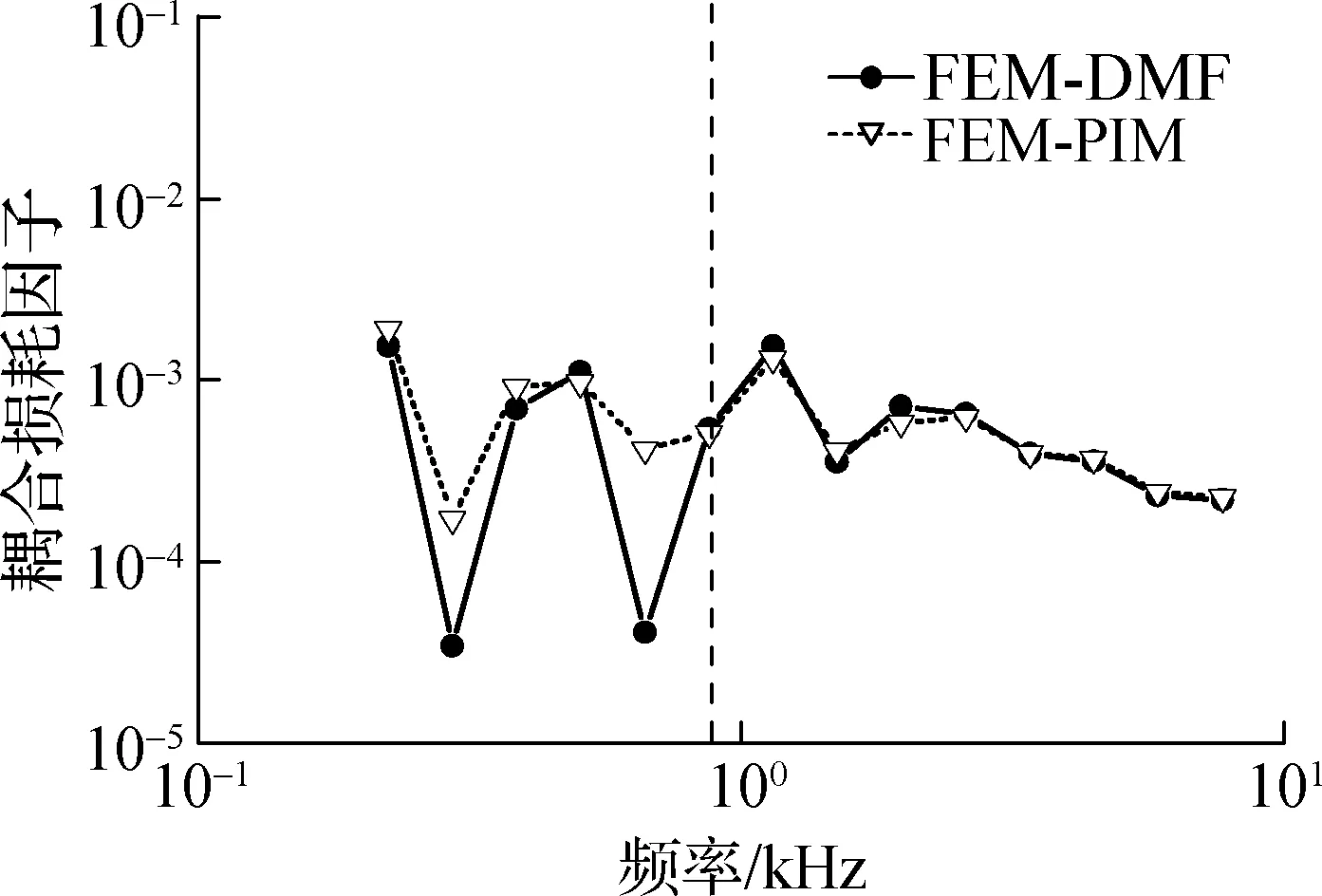
图10 耦合损耗因子

计算结果表明:FEM-DMF方法与FEM-PIM预示得到的耦合损耗因子变化趋势基本一致,在频率大于1.25 kHz频段内,二者的计算结果相差小于1 dB;在小于1.25 kHz频段,二者的计算结果相差较大,这主要是由于结构在频段内模态阶数小于5,未能满足模态能量均一化假设.从计算效率方面来看,FEM-DMF方法的运行程序时间约为15 min,而FEM-PIM需要约2 h.FEM-DMF方法的计算效率提高了87.5%.因此,FEM-DMF方法在其适用范围内能够高效准确地预示复杂结构的耦合损耗因子.

3 结论

1) 在满足模态能量均一化假设的频带内,随着L型耦合板的子系统刚度比和结构阻尼的增大,FEM-DMF方法的预示精度不断提高.

2) 在满足模态能量均一化假设的频带内,随着L型耦合板阻尼的增大,满足耦合损耗因子预示精度的临界刚度比逐渐减小.当结构阻尼为0.01时,临界刚度比为9,基于FEM-DMF方法预示的耦合损耗因子误差小于1 dB.

3) 对于L型耦合加筋板,在满足模态能量均一化假设的频带内,基于FEM-DMF方法预示的耦合损耗因子误差小于1 dB.而与FEM-PIM相比,FEM-DMF方法的计算效率提高了87.5%,从而说明FEM-DMF方法在其适用范围内能够准确高效地预示复杂结构的耦合损耗因子.

)

[1] Lyon R H, Dejong R G.Theoryandapplicationofstatisticalenergyanalysis[M]. London: Butterworth-Heinemann, 1995: 3-16.

[2] 张婧雯, 孟光, 游进, 等. 基于统计能量法的声场-结构耦合模型高频振动隔振分析[J]. 振动与冲击, 2009, 28(12): 19-22. DOI:10.3969/j.issn.1000-3835.2009.12.006.

Zhang Jingwen, Meng Guang, You Jin, et al. Analysis on high frequency vibration isolation of coupled sound cavity-structure model based on statistical energy method [J].JournalofVibrationandShock, 2009,28(12): 19-22. DOI:10.3969/j.issn.1000-3835.2009.12.006. (in Chinese)

[3] 马兴瑞, 韩增尧, 邹元杰, 等. 航天器力学环境分析与条件设计研究进展[J]. 宇航学报, 2012, 33(1): 1-12. DOI:10.3873/j.issn.1000-1328.2012.01.001.

Ma Xingrui, Han Zengyao, Zou Yuanjie, et al. Review and assessment of spacecraft mechanical environment analysis and specification determination [J].JournalofAstronautics, 2012,33(1): 1-12. DOI:10.3873/j.issn.1000-1328.2012.01.001. (in Chinese)

[4] 张娟, 李天匀, 朱翔, 等. 基于AutoSEA2的船舶典型动力源辐射噪声分析[J]. 船舶力学, 2008, 12(5): 819-823. DOI:10.3969/j.issn.1007-7294.2008.05.021.

Zhang Juan, Li Tianyun, Zhu Xiang, et al. Analysis of sound radiation induced by typical engine in the ship on the basis of AutoSEA2 [J].JournalofShipMechanics, 2008,12(5): 819-823. DOI:10.3969/j.issn.1007-7294.2008.05.021. (in Chinese)

[5] 向树红, 王大钧, 于丹, 等. 统计能量分析参数的综合确定方法及应用[J]. 振动工程学报, 2004, 17(4): 477-482. DOI:10.3969/j.issn.1004-4523.2004.04.021.

Xiang Shuhong, Wang Dajun, Yu Dan, et al. Comprehensive method of statistical energy analysis parameters determination and its applications [J].JournalofVibrationEngineering, 2004,17(4): 477-482. DOI:10.3969/j.issn.1004-4523.2004.04.021. (in Chinese)

[6] 江民圣, 牛军川, 郑建华, 等. L型耦合板结构能量传递系数特性的研究[J]. 振动与冲击, 2015, 34(17): 131-136. DOI:10.13465/j.cnki.jvs.2015.17.022.

Jiang Minsheng, Niu Junchuan, Zheng Jianhua, et al. Energy transfer coefficients’ features of L-shaped coupled plates [J].JournalofVibrationandShock, 2015,34(17): 131-136. DOI:10.13465/j.cnki.jvs.2015.17.022. (in Chinese)

[7] Pankaj A C, Sridhar S, Murigendrappa S M. A comparison of different methods for determination of coupling factor and velocity response of coupled plates [J].JournalofVibroengineering, 2013,15(4): 1885-1896.

[8] Mace B R, Shorter P J. Energy flow models from finite element analysis [J].JournalofSoundandVibration, 2000,233(3): 369-389. DOI:10.1006/jsvi.1999.2812.

[9] Bies D A, Hamid S. In situ determination of loss and coupling loss factors by the power injection method [J].JournalofSoundandVibration, 1980,70(2): 187-204. DOI:10.1016/0022-460x(80)90595-7.

[10] Lalor N. The experimental determination of vibrational energy balance in complex structures [C]//StressandVibration:RecentDevelopmentsinMeasurementandAnalysis. London: International Society for Optics and Photonics, 1989: 302-314.

[11] 张鹏, 费庆国, 李彦斌, 等. 材料物性热效应对统计能量分析参数的影响[J]. 振动与冲击, 2016, 35(24): 73-78. DOI:10.13465/j.cnki.jvs.2016.24.012.

Zhang Peng, Fei Qingguo, Li Yanbin, et al. Effect of temperature-dependent material property on statistical energy analysis parameters [J].JournalofVibrationandShock, 2016,35(24): 73-78. DOI:10.13465/j.cnki.jvs.2016.24.012. (in Chinese)

[12] 陈强, 张鹏, 李彦斌, 等. 基于FEM-PIM计及热效应的统计能量分析[J]. 航空动力学报, 2017, 32(6): 1366-1374.

Chen Qiang, Zhang Peng, Li Yanbin, et al. Statistical energy analysis under thermal environment based on FEM-PIM [J].JournalofAerospacePower, 2017,32(6): 1366-1374. (in Chinese)

[13] Maxit L, Guyader J L. Estimation of SEA coupling loss factors using a dual formulation and FEM modal information Part 2: Numerical applications [J].JournalofSoundandVibration, 2001,239(5): 931-948. DOI:10.1006/jsvi.2000.3193.

[14] 孔宪仁, 王英诚, 张红亮. 基于DFM/FEM铝蜂窝夹层结构耦合损耗因子预测[J]. 振动与冲击, 2016, 35(1): 125-131. DOI:10.13465/j.cnki.jvs.2016.01.021.

Kong Xianren, Wang Yingcheng, Zhang Hongliang. Coupling loss factors estimation of aluminum honeycomb sandwich structures using DFM/FEM [J].JournalofVibrationandShock, 2016,35(1): 125-131. DOI:10.13465/j.cnki.jvs.2016.01.021. (in Chinese)

[15] Maxit L, Guyader J L. Estimation of SEA coupling loss factors using a dual formulation and FEM modal information. Part 1: Theory [J].JournalofSoundandVibration, 2001,239(5): 907-930. DOI:10.1006/jsvi.2000.3192.

[16] 姚德源, 王其政. 统计能量分析原理及其应用 [M]. 北京: 北京理工大学出版社, 1995: 2-7.