基于模糊层次分析法的高速切削速度优选研究*

张世伟，汪永超，袁 彪

(四川大学 制造科学与工程学院，成都 610065)

0 引言

随着工业现代化的快速发展，零件的形状越来越复杂，精度要求越来越高，高速切削也就变得越来越重要。高速切削已成为21世纪机械制造业一场具有深远影响的技术革命[1]。切削速度是切削用量三要素之一，切削速度与切削力的关系决定了切削过程中所消耗的功率和加工工艺系统的变形，同时，切削力还直接影响切削热的产生，并进一步影响刀具的磨损、破损、刀具耐用度等，对加工精度和加工质量有着直接的影响。文献[2]指出，在切削速度较低的情况下，切削力随转速的增加而升高，但达到某一临界速度值后，随着转速继续增大，切向切削分力反而下降。由此，如何达到高速切削的低成本、高效率、低消耗、高质量取决于切削速度的选择。

目前，对切削速度的选择研究比较有限，M.Alberti[3]以及K.Wu[4]等人主要从高速切削参数的优化进行了研究，没有更进一步对切削速度的选择进行深入的研究，牛印宝等采用层次分析法和灰色关联分析法以绿色制造为准则对切削速度进行选择[5],郭建英等基于刀-屑摩擦与切削速度关联模型的切削力数值分析进行选择[6]。前者的研究没有考虑层次分析方法的收敛性，后者没有综合考虑各个指标对切削速度的影响。而模糊层次分析法在多目标单指标的优化选择中取得了大量成果，例如：王化吉等人运用模糊层次分析法对汽车操纵稳定性进行分析评价[7]，李磊等人运用模糊层次分析法对机械材料选择进行分析优化[8]，很少有人将这种方法运用在高速切削速度的优选研究中。所以，本文在前人研究的基础上，将模糊层次分析法运用到高速切削速度的选择上来，就高速切削最优切削速度与最短加工时间，最低生产成本，最少能源消耗，最好加工质量和最轻环境污染这一问题建立数学模型，基于模糊层次分析法对模型进行分析和求解。

1 建立指标优化体系

在满足生产工艺需求的条件下，切削速度的选择范围很广，不同的切削速度需要的加工时间，加工成本，能源消耗，加工质量和环境污染都不同，因此，在高速切削加工时，选择切削速度要综合考虑多个决策因素，然后对各个可选的切削速度进行分析、对比和决策，找出最佳切削速度，使得高速切削加工过程的总体效果最好。

首先建立一套指标决策优化体系，本文从加工时间、加工成本、加工质量、能源消耗、环境污染5个方面进行综合评价，同时，各评价目标自身又包含影响因素子集，故需继续划分。如图1所示。

图1 切削速度优选层次结构模型

2 模糊层次分析法(FAHP)

层次分析法[9](AHP)是由美国著名的运筹学家SAATY 教授于20世纪70年代中期提出的一种定性和定量相结合、系统化的、层次化的分析方法。模糊层次分析法(FAHP)是将模糊理论与传统层次分析法相结合、充分考虑人思考的模糊性的一种理论方法。目前，模糊层次分析法分为两大类，一类是基于模糊数的模糊层次分析法，另一类是基于模糊一致矩阵的模糊层次分析法。本文选用一种基于三角模糊数互补判断矩阵的方法，来确定高速切削最优切削速度评价指标的权重系数。

2.1 建立模糊判断矩阵

模糊判断矩阵建立的基础是矩阵中元素的标度方法。在使用 FAHP构造判断矩阵时，所给出的判断常常是以区间数或模糊数的形式表示。由于三角模糊数[10]既包含区间的概念，又通过中值体现指标间相互比较的最可能关系。经过同专家人员的交流，发现三角模糊数的这一特点能够较好地体现主观评价人员对于指标间重要关系的理解。因此，本文选用基于三角模糊数的FAHP标度方法，将模糊判断矩阵中的元素以三角模糊数来表示。三角模糊数用(l,m,u)来表示，l和u为其上界值和下界值，m为其中值。在本文应用此概念建立的模糊判断矩阵中，三角模糊数的中值表示两指标比较最可能的重要程度关系，模糊数上下界表示两指标相对重要程度关系范围，中值的选取依据表 1所示的模糊标度。在建立模糊判断矩阵的过程中，根据专家的经验首先确定三角模糊数的中值，再确定其上下界值，从而确定两指标的相对重要程度。比如，比较优化层K1，K2，……，Kn相对于目标层V两两之间的重要性，可以得到一个K=(kij)n×n三角模糊互补判断矩阵。该矩阵具有如下性质：

(1)kij+kji=1,kij>0,i,j∈N

(2)kij=(klij,kmij,kuij),kji=(klji,kmji,kuji),klij+kuji=

kmij+kmji=kuij+klji=1且klij≥kmij≥kuij>0，i,j∈N

表1 模糊标度值及其含义

2.2 模糊互补判断矩阵一致性检验及调整

对于模糊判断矩阵K=(kij)n×n,若对任意k有:

kij=kik-kjk+0.5，1≤k≤n

(1)

(2)

通过以上公式变换调整可得模糊互补一致判断矩阵R=(rij)n×n。

2.3 层次各指标权重值确定

根据徐泽水[12]三角模糊数互补判断矩阵的一种排序方法给出的权重值计算方法进行计算，求出各子指标三角模糊数权重向量。

(3)

2.4 层次总排序确定最终方案

层次总排序是将各层次相关联指标的权重值相乘得到的,需从上到下逐层进行排序直至最低层次素。如假设层次结构有n个层次(目标层为第一层),则各层次(不包含目标层)的层次总排序权重为:

W=W(n)W(n-1)…W(2)

(4)

2.5 各方案得分确定

根据各方案的子指标值得分可建立矩阵RT

S=1000W·RT= (V1,V2,…,Vn)

(5)

Vop=maxVi,i=1,2,…,n

(6)

其中，S为方案得分向量,Vn是各方案对应的得分，所以，最佳方案是根据最高得分值Vop确定的。

3 案例分析

某加工中心计划加工一批航空发动机涡轮叶片，既要保证加工质量，又要按期保质完成，同时，由于加工中心设备昂贵，如果切削速度选的不合适容易造成刀具磨损甚至折断。为了科学有效的完成此项工作，通过查阅资料获得切削速度范围为450～520m/min,结合加工中心经验，有4种方案可供选择，因此，需要评定出最佳切削速度。

3.1 模糊评价

依据丰富经验的机加师傅按照十分制打分方法对4种切削速度的主观评测综合评价结果如表2所示。

表2 最佳切削速度主观评价模糊层次结构及评分

3.2 建立模糊判断矩阵

根据三角模糊互补判断矩阵构建方法根据表1的模糊标度，构造各指标两两比较的判断矩阵，如表3～表7所示。

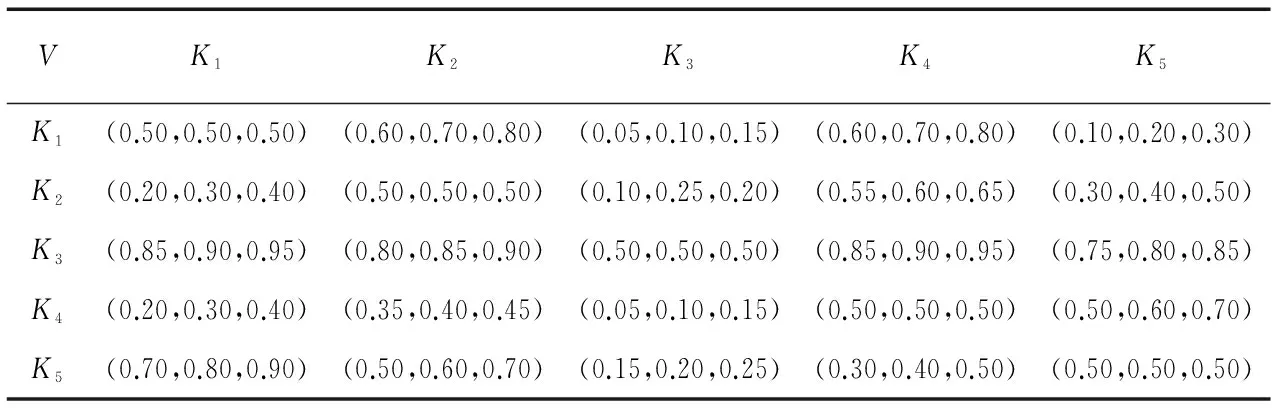
表3 最佳切削速度各指标判断矩阵

表4 加工时间各指标判断矩阵

表5 加工成本各指标判断矩阵

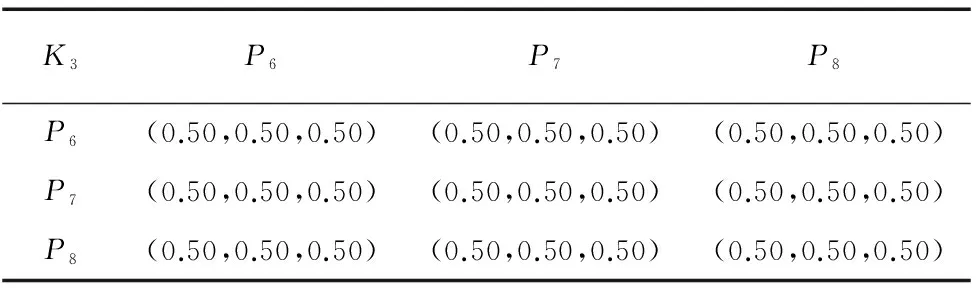
表6 加工质量各指标判断矩阵

表7 环境污染各指标判断矩阵

3.3 计算各指标权重值

按照公式(3)计算各子指标的权重值ωi(i∈N)，可得出:

优化层指标权重值：

ω2=(0.124,0.230,0.376,0.122,0.157)

底层指标权重值：

ω3=(0.65,0.35,0.55,0.25,0.20,
0.33,0.32,0.35,1.00,0.67,0.33)

3.4 层次总权重值

根据指标层和子指标层的层次单排序结果按照公式(4)可得到各层次的层次总权重值,如表8所示。

3.5 子指标评价打分

子指标值得分的确定和指标值得分的确定方法是一样的,唯一不同的是指标的判断矩阵是各指标互相比较得到的,根据各子指标总权重值确定子指标得分，分值表如表9所示。

3.6 各方案得分确定

根据各方案的子指标值得分可建立矩阵RT,根据公式(5)和子指标总权重值计算得：

W=ω3.ω2=(0.081,0.043,0.127,0.058,0.046,
0.121,0.117,0.128,0.122,0.105,0.052)

S=1000W·RT=(58.29,69.49,80.68,74.12)

表8 各层次指标权重

表9 子指标得分

显然V3得分最高，可确定为4种可选速度中的最佳切削速度。通过实验证明，四种可选切削速度的加工综合效益以V3为最优，而在案例实际工作中，论文所选出的切削速度在加工过程也取得了理想的效益，因此，验证了所提出方法的可行性和有效性。

4 结论

本文主要是解决了在高速切削加工航空高密零件时手册规定的切削速度范围内选出最佳切削速度提出一种方法。论文分析了影响切削速度的影响因素，基于模糊层次分析法建立了一种两级结构的多目标优化模型，并采用三角模糊数建立判断矩阵，使决策者更加具体化合理化的做出决定，避免主观评价模糊性带来的不利影响，实践证明基于模糊层次分析法的评价模型和评价算法用于高速切削加工中切削速度的优选是实用的，因此也证明了使用该方法用于切削速度优选是可行的和有效的。

[1] 张宁菊.高速切削机床的关键技术[J].机床与液压,2005(11):20-21,113.

[2] 刘战强,万熠,艾兴.高速铣削中切削力的研究[J].中国机械工程,2003,14(9):734-736.

[3] M Alberti, J Ciurana, M Casadesus. A system for optimising cutting parameters when planning milling operations in high-speed machining[J].Journal of Materials Processing Technology,2005(1):23-30.

[4] K Wu,Ning He,W H Liao,et al. Optimization of Cutting Parameters in High Speed Milling of Thin-Walled Structure Components[J].Key Engineering Materials,2003(7):809-811.

[5] 牛印宝,汪永超,王宇,等.面向绿色制造的切削速度优化选择研究[J].机床与液压,2014,42(23):42-45.

[6] 郭建英,吕明.基于刀-屑摩擦与切削速度关联模型的切削力数值分析[J].制造技术与机床,2014(5):75-79.

[7] 王化吉,宗长富,管欣,等.基于模糊层次分析法的汽车操纵稳定性主观评价指标权重确定方法[J].机械工程学报,2011,47(24):83-90.

[8] 李磊,汪永超,唐雨,等.基于模糊层次分析法的机械材料选择[J]. 组合机床与自动化加工技术,2015(11):8-12.

[9] 张吉军.模糊层次分析法[J].模糊系统与数学,2000(2):80-88.

[10] 徐泽水.模糊互补判断矩阵排序的一种算法[J].系统工程学报,2001,16(4):311-314.

[11] 王晓燕,胡付飞,郑耀辉,等.基于模糊层次分析法的刀具优选技术研究[J].组合机床与自动化加工技术,2016(1):29-32.

[12] 徐泽水. 三角模糊数互补判断矩阵的一种排序方法[J].模糊系统与数学,2002(1):47-50.