基于半径约束的空间圆弧位姿视觉检测算法*
2018-01-29刘凌云吴岳敏李慧玲
刘凌云,罗 敏,吴岳敏,李慧玲,马 彬
(湖北汽车工业学院 电气工程系,湖北 十堰 442002)
0 引言
空间圆弧在图像处理中是一种特征明显且容易识别的形状,而机械零部件的基本特征孔、平面正交即可形成空间圆或圆弧,因此通过对机械零部件上空间圆弧的视觉位姿检测,间接获取机械零部件的空间位置和姿态,在机器人视觉定位、目标跟踪、视觉避障中具有广泛的应用。目前针对空间圆弧的视觉位姿检测的研究,主要可以分为两类,一类是对空间圆弧上特征点在不同图像中图像点进行匹配的立体匹配算法[1-3],通常计算复杂度较大且所需硬件成本较高;另一类是针对单个圆特征,利用其它约束条件进行空间圆姿态信息计算并消除二义性[4-8],如邢德奎等[5]提出使用同心圆目标快速、准确地获取圆心点在图像中的准确的投影点位置;魏振忠[6]提出了一种基于空间角度约束以消除空间圆姿态二义性的方法。
而对于大多数机械零部件而言,其特征平面与特征孔正交所形成的为一个或多个单一的空间圆或圆弧,而非同心圆,且空间圆或圆弧的半径为确定值。因此对同一平面内半径已知的多个空间圆或圆弧进行视觉位姿测量具有一定的工程实用价值。这里提出一种以位于同一平面内不同心的两个半径已知的圆互为约束,并借助于空间圆弧到虚拟像机中影像的映射数学模型,通过参数交叉迭代、分层搜索的优化算法求取空间圆弧位姿的检测方法。
1 空间圆在虚拟像机中的映射数学模型
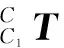
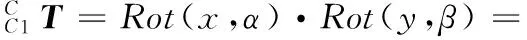
(1)
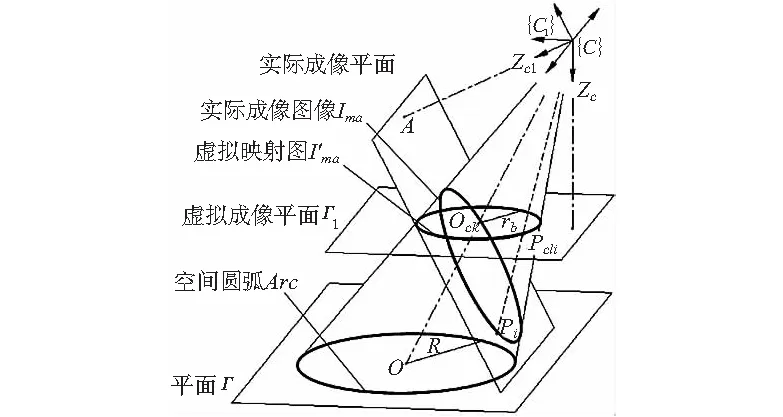
图1 空间圆弧在虚拟像机中成像数学模型

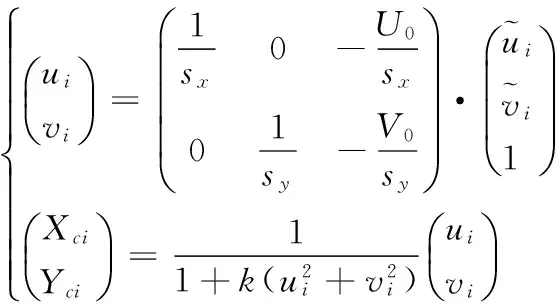
(2)

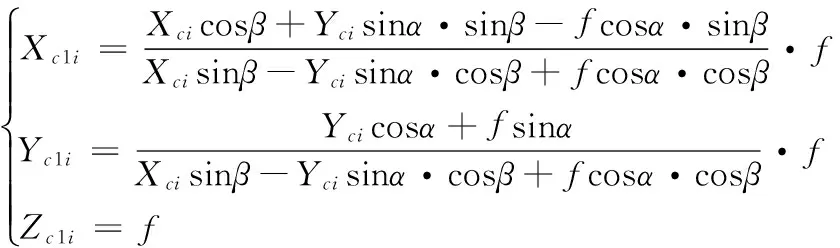
(3)
由射影几何原理[9]可知,虚拟映射点pc1i也是实际空间圆弧Arc上的点在虚拟摄像机{C1}中的影像,且当虚拟成像平面Γ1与空间圆弧Arc所在平面Γ平行(令此时α=αb、β=βb)时,虚拟映射点序列pc1i正好位于同一圆弧上。此时虚拟成像平面Γ1的法向量在坐标系{C}中的描述Cl即为圆弧Arc的姿态描述,虚拟映射点序列pc1i所构成圆的圆心即为实际空间圆圆心的图像点。
2 虚拟摄像机最佳姿态参数的求取
为了借助于虚拟成像平面Γ1与空间平面Γ平行关系求取空间圆弧Arc的位姿,本文提出了对虚拟映射序列点pc1i进行圆拟合,并构造拟合圆的圆度误差函数[10],以圆度误差最小为目标,在有效搜索范围内对姿态参数α、β进行优化,从而得到虚拟摄像机姿态的最佳值αb、βb。
2.1 α、β有效搜索范围的确定
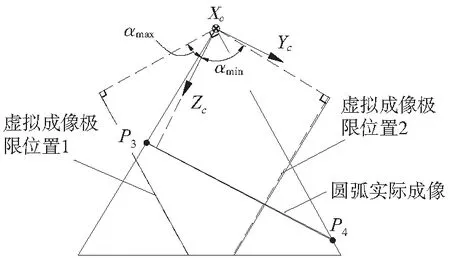
图2 α角度极限范围的确定
当虚拟成像平面分别平行于过P3或P4的射线时对应的α转角即为其极限角度αmin、αmax,即满足关系式(4):

(4)
同理可以求出姿态参数β的极限角度βmin、βmax满足关系式(5):
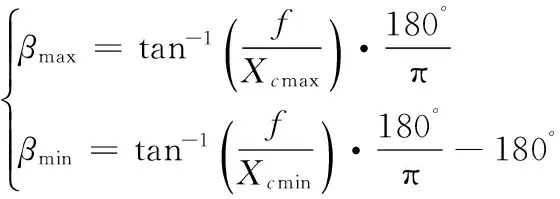
(5)
2.2 α、β交叉迭代分层搜索算法
对于单峰值范围内α、β最佳值的搜索,为了提高寻优速度,减小计算负荷,文中提出了一种采用α、β交叉迭代的分层搜索策略。假设初始步距为S0,每层步距成等比减小,等比系数0 (6) 再根据公式(4)、公式(5)计算姿态参数α、β的初始搜索范围(αmin,αmax)、(βmin,βmax)后,则取初始最佳姿态βb=βmin或βmax,依次完成步骤①~⑤,迭代求取位姿参数α、β的最佳值。 ①令β=βb,当α在(αmin,αmax)范围内以S0为步距进行等间距取样的过程中,根据公式(3)依次求取虚拟映射点pc1i的坐标(Xc1i,Yc1i,Zc1i);对虚拟映射点pc1i进行圆拟合,并求取圆度ej(其中j=1,2,3…M;M为α的取样数),将圆度ej中的极大值e1所对应的α值设为αb; ②令α=αb,当β在(βmin,βmax)范围内以初始步距S0进行等间距取样的过程中,重复步骤①,并将系列拟合圆中圆度极大值e2所对应的β值设为βb; ③当|e2-e1|>ε(ε为某一极小值)时返回步骤①; ④分层搜索次数m++;当m>N2时,跳到步骤⑤,否则取步距Sm=qm·S0,搜索范围αmin=αb-S0*q(m-1),αmax=αb+S0*q(m-1),βmin=βb-S0*q(m-1),βmax=βb+S0*q(m-1),返回步骤①; ⑤获取最佳姿态参数αb、βb,并将该姿态下所对应的拟合圆半径rk设置为rb、圆心ock的坐标设为(c1Xob,c1Yob,f)T。 当α、β姿态参数分别取最佳姿态参数αb、βb时,即空间圆弧Arc所在平面Γ与虚拟成像平面Γ1处于平行状态时,圆弧Arc的姿态可由虚拟摄像机坐标系{C1}的Z轴单位主矢量在摄像机坐标系{C}中的描述Cl来比表示。由公式(1)可知: (7) (8) 图3 遍历搜索时圆弧影像圆度与姿态参数的关系曲线 采用α、β交叉迭代运算前,首先利用分层搜索算法[11]将圆度函数的两个峰值区域分割开来,然后在圆度函数单峰值区域1、2内分别采用交叉迭代搜索,圆度极大值Fm、最佳姿态参数αb、βb与迭代次数的关系曲线如图4所示(步距S=0.16°时),由关系曲线可知该交叉迭代算法具有较强的收敛性,经过少量几次交叉迭代,圆度最大值、最佳姿态参数αb、βb即达到稳定值,从而有效的缩少了搜索范围。 (a) 区域1内迭代搜索时 (b) 区域2内迭代搜索时图4 圆度最大值与交叉迭代参数的关系曲线 取初始步距S=4°、步距等比系数q=0.2,在圆度函数的两个单峰值区域对姿态参数α、β分别采用交叉迭代分层搜索,获得的实验数据如表1中所示。 即经过三次分层,缩小范围进行搜索,姿态参数α、β的检测精度可达到±0.16°,耗时仅为46.6s。若采用全范围遍历搜索或交叉迭代搜索算法达到同样的测量精度,计算机CPU所需的时间开销分别为184.5s和72.8s。 将两组最佳姿态参数Arfa_b、Beita_b分别代入公式(7)、公式(8)可获得圆弧Arc的姿态描述及圆心位置坐标的两种解,如表2所示。 由表2可知,解2所求位姿数据与理论值相比,位置度误差为0.0227mm,角度误差为0.0683°,误差来源主要为搜索过程中步距误差和计算舍入误差。 表1 α、β交叉迭代分层搜索实验数据 续表 表2 求取的圆弧Arc最佳位姿信息数据表 为了消除空间圆姿态检测的二义性问题,可充分利用待检测对象同一表面多孔的特点,以两个不同心的圆或圆弧互为约束,应用上述算法正确获取空间圆或圆弧所在平面的正确姿态。如某汽车零件上平面的两孔A、B直径均为φ8.246mm,孔间距19.023mm,图5为实际采集的该零件图像。 (a) 实际采集图像 (b) A、B圆弧轮廓上特征点提取图5 圆弧位姿检测实测图像及处理 分别对A、B两孔进行子像素轮廓提取后等间距采样获取圆弧上图像点序列。采用与仿真实验中相同的摄像机内参进行实物验证。针对两组图像点序列分别应用文中所述圆弧位姿视觉检测算法(取检测精度Acc<0.1°),求取A、B两孔姿态信息,并针对姿态公共解求取两孔圆心的位置信息,如表3中所示。 另外改变工件的位置和姿态进行多次测量,所获得的A、B孔孔间距测量误差均小于0.08mm,姿态公共解的相对误差均小于0.2°。 表3 孔A、B位姿检测数据表 由此可见,采用上述算法求取空间圆的位姿信息具有较好的精度,也证实了该算法对于消除空间圆姿态二义性是切实可行的。另外,除了包括摄像机内部参数的标定误差、特征轮廓提取误差及计算误差外,位姿检测误差主要来源还包括分层搜索时最终采用的步距。步距越小,检测精度越高,CPU时间开销也越大。 本文提出了一种在已知摄像机内部参数的情况下,仅通过对同一平面内不同心的多个圆或圆弧的一次成像,实现空间圆所在平面的姿态检测,若空间圆的半径已知,可实现空间圆圆心位置的检测。和传统的空间圆弧位姿检测算法相比,本文提出的空间圆弧位姿检测算法不需要复杂的数学计算,收敛性强,且在圆弧识别、抗遮挡等方面具有明显优势,并能准确获取空间圆弧在摄像机坐标系中的位姿信息。该检测算法特别适合于同一表面具有多孔特征的对象的位姿检测或孔间距检测。 [1] HEIKKIL A J, SILVEN O. A four-step camera calibration procedure with implicit image correction[C].IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 1997:1106-1112. [2]周富强,张广军,江洁.空间圆几何参数的非接触高精度测量方法[J].仪器仪表学报,2004,25(5):604-607. [3]单宝华,袁文厅,刘洋.一种基于实心圆靶标的立体视觉系统标定方法[J].光学学报,2016,36(9):0915001. [4]KIM J S,GURDJOS P.Geometric and algebraic constraints of projected concentric circles and their applications to camera calibration[J].IEEE Trans Pattern Analysis and Machine Intelligence, 2005,27(4):637-642. [5]邢德奎,达飞鹏,张虎. 圆形目标精密定位方法的研究与应用[J].仪器仪表学报,2009,30(12):2593-2598. [6]魏振忠,赵征,张广军. 空间圆姿态识别二义性的角度约束消除[J]. 光学精密工程,2010, 18(3) :685-691. [7]陈新禹,马孜,胡英,等.视觉测量中圆形标记点的高精度定位[J]. 光电子.激光, 2013,24(8):1524-1528. [8]刘子腾,白瑞林,王秀平.视觉标定中圆心投影点精确定位[J].激光与光电子学进展,2015,52(9):091001. [9]何春华,张雪飞,胡迎春.基于改进Sobel算子的边缘检测算法的研究[J]. 光学技术,2012,38(3):323-327. [10]陈天飞,赵吉宾,王银灵,等.基于射影变换圆阵靶标中心像点的计算[J].仪器仪表学报,2015,36(4): 895-902. [11]郑静娜,李红玉,郑斯文,等. 利用回溯搜索优化算法(BSA) 测量圆度误差[J].辽宁大学学报(自然科学版),2015,42(4):320-324. [12]刘凌云,钱新恩,罗敏.确定对象单目视觉位姿检测算法的研究[J].中国机械工程,2010,21(23):2825-2829. [13] 夏仁波,刘伟军,赵吉宾,等.基于圆形标志点的全自动相机标定方法[J].仪器仪表学报,2009,30(2):368-373. [14]徐鹏,汪建业,王燕儒.摄像机标定中靶标圆心像点坐标的精确计算[J].红外与激光工程,2011,40(7): 1342-1346. [15]韩建栋,杨红菊.三维视觉测量中圆中心投影误差分析方法[J].计算机科学,2010,37(12):247-249. [16]李占利,刘梅,孙瑜.摄影测量中圆形目标中心像点计算方法研究[J].仪器仪表学报,2011,32(10):2235-2241.3 空间几何圆位姿参数的求取
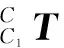
4 仿真验证实验
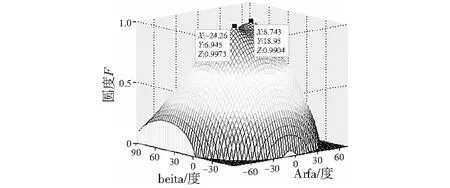
4.1 交叉迭代次数对检测精度影响的仿真实验
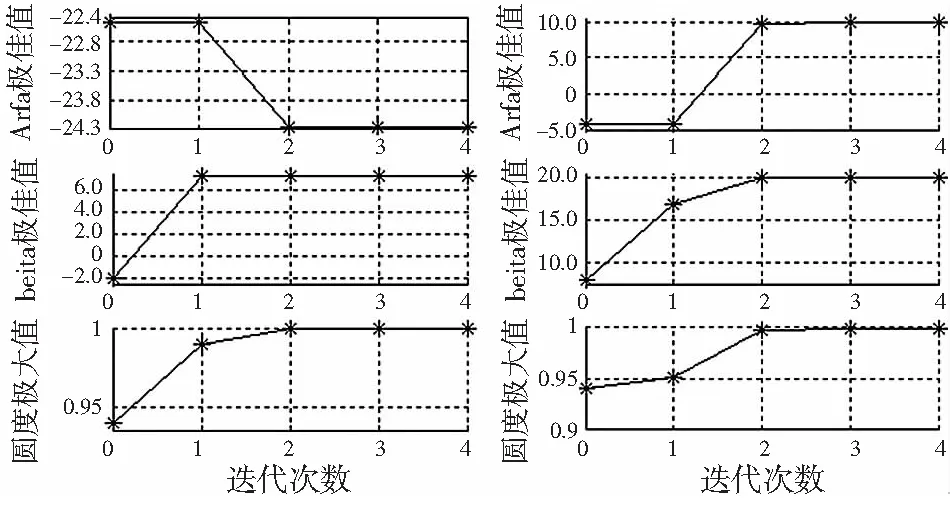
4.2 交叉迭代分层搜索效果的仿真实验

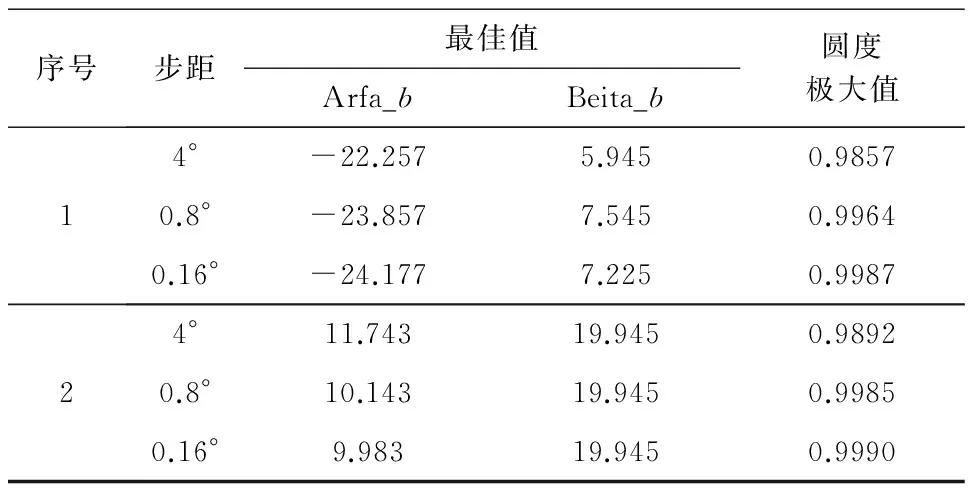

4.3 实物实验


5 结论
