一种新型滑模观测器的永磁同步电机无位置传感器控制

王丽华，王苏洲

( 南京工业大学 电气工程与控制科学学院 ，南京 211816)

0 引言

永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)因其具有效率高、功率大和动态响应快等优点得到了广泛的应用[1]。常规的电机控制法多使用位置传感器直接对转子的位置或者是转速信号进行检测，导致电机体积变大和生产成本增加，所以在PMSM控制中对于无位置传感器控制方法的研究意义重大。如今国内外许多研究人员对无位置传感器控制技术进行了深入研究，其中主流的方法主要有状态观测器法、神经网络控制法、自适应控制法和滑模观测器法等[2]。其中，滑模观测器凭其鲁棒性强、算法简单、动态响应较快以及实现容易等优势，逐渐得到青睐[3]。但是以往滑模观测器主要使用开关函数，在切换过程中由于函数不连续的开关特性导致观测器中的状态估计值出现严重的“抖振”现象。文献[4]将边界层引入到滑模控制中，使用连续的Sigmoid函数取代开关sgn函数，边界层外仍采用滑模控制，虽然此法可以在一定程度上减弱“抖振”，但是边界层的取值过小或是控制量过大，致使滑模观测器的鲁棒性无法得到保证。文献[5]使用线性化的函数代替非线性控制，虽降低切换控制影响，提高了系统的稳态和动态性能，但其设计复杂，计算量过大。文献[6]提出了一款具有变截比频率的低通滤波器，通过对获得的电机反电动势进行滤波处理，但是在消除抖振的同时，也将使被观测量相位滞后以及幅值减小。

本文在对传统滑模观测器进行改进的基础上，提出了一种基于新型滑模观测器的PMSM无位置传感器控制法。将混合非奇异终端滑模面应用到传统的线性滑模面上，同时也设计出滑模控制律，有效的削弱了滑模控制器中存在的“抖振”，利用Lyapunov理论对所设计的新型滑模观测器进行稳定性证明。仿真结果表明本文设计的新型滑模观测器可以准确的估算出电机的转子位置和转速。

1 永磁同步电机传统滑模观测器

根据PMSM数学模型分析各个物理量间的关系，是对其进行无传感器控制的前提。在静态坐标系(α-β)下，永磁同步电机的数学模型可表示如下[7]：

(1)

其中，Rs表示电机的定子电阻，L表示电机的定子电感，iα和iβ表示定子电流，uα和uβ表示定子的电压，eα和eβ表示反电动势大小。

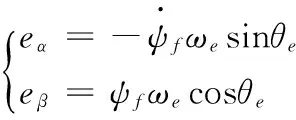
(2)

其中，ωe=pnωr/2表示电机的电角度速度；ψf表示永磁同步电机的磁链；θe表示电机的转子电角度。

电机转子的速度和位置相关的数据包含在电机的反电动势中，通过设计滑模观测器观测电机反电动势，可以对电机转子位置与速度大小进行估计。在静态坐标系下永磁同步电机的数学表达式可如下：

(3)

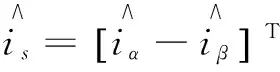
(4)

(5)

(6)

由式(6)可得符号函数式不连续的变化量，存在大量的高频扰动，所以要想获得平滑的反电动势信号需要对其进行低通滤波，经过处理以后得到的反电动势估计表达式为[8]：

(7)

其中，

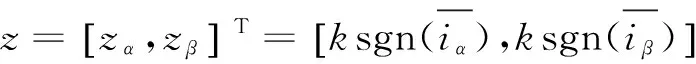
(8)

(9)

在低通滤波器的作用下，随着转速的变大将会导致反电动势的幅值衰减，因此必须对电机转速进行补偿。采用的低通滤波器表达式如下：

(10)

根据式(2)可推算出转速和转子位置的估算方程为(11)和式(12)：

(11)

(12)

同样，在低通滤波器作用下，也会导致反电动势的相位之后，必须对表达式(12)转角估计值进行补偿。补偿后的转角值表示如下：

(13)

其中，ωcutoff=1/τ表示截止频率。

通过以上对常规滑模观测器设计过程的介绍，为了解决“抖振”问题通常引入低通滤波器，导致系统相位之后，虽然进行了补偿，但是使得系统的复杂程度增加，降低了系统观测的准确度。

2 新型滑模观测器的设计与优化

2.1 新型滑模观测器的构建与稳定性分析

针对永磁电机无位置传感器控制中存在的电机转速和位置估算误差较大的问题，本文设计了一种新型二阶滑模观测器，它不仅能消除滑模“抖振”现象，而且由于不采用滤波器，避免了相位滞后[9]。二阶滑模观测器系统如图1所示。

图1 新型二阶滑模状态观测器系统框图

模观测器的设计可用方程表示为:

(14)

(15)

本文将混合非奇异终端滑模面应用到传统的线性滑模面上，设计了表达式(16)所示的滑模切换面：

(16)

其中，S=[Sα，Sβ]T，k表示积分增益系数。

根据表达式(15)可知电机误差状态系统，选择式(16)为滑模面，滑模观测器的控制律设计如式(17)～式(19)所示，那么电机定子电流误差将会收敛为0。

z=zeq+zsw

(17)

(18)

(19)

其中，sgn(s)=[sgn(sα),sgn(sβ)]T；η=ε+ξ；

利用Lyapunov方法证明所设计滑模观测器的稳定性，定义函数为：

(20)

对式(20)进行求导可得：

(21)

(22)

由式(15)、式(17)～式(19)可得到下面的表达式:

(23)

则：

(24)

将表达式(24)代入表达式(22)，可得:

(25)

(26)

当系统收敛时，反电动势可表达如下：

(27)

(28)

所以电机转子位置可由如下计算得出：

(29)

(30)

2.2 转子位置与速度数据的获取

在分析滑模控制基础理论后，根据本文设计的控制律(19)，二阶滑模切换面S在一定的时间内将会收敛于平衡点，对滑模切换面的表达式(16)进行修改：

(31)

es=-z

(32)

从表达式(32)通过观测滑模控制律能够获得反电动势的数据信息。与表达式(6)相比，传统的滑模观测器的反电动势数据信息存在不连续的符号函数中，虽然新型滑模控制律同样存在符号函数，但是积分器已经对该符号进行了滤波处理，有效的抑制了抖振。所以，转子位置可以通过计算观测到的反电动势信息获得，不再需要进行低通滤波处理，也解决了传统滑模观测器相位滞后的问题[10]。

图2 转子的位置与速度跟踪算法结构图

通过对图2算法分析可得：

(33)

(34)

此时图2的跟踪算法等效于图3的锁相环结构。采用PI对转子位置误差Δθre进行调节后可得到估算转速，再对估算转速进行积分可以获得估算转子位置。当估算的转子位置比实际转子位置偏小时，那么位置误差将会增大，经过PI调节后的转速也会偏大，进而调节的转子位置偏差也会逐渐偏大，最终使其与实际转子位置相接近；相反，若果估算转子位置比实际位置大，分析相似。

图3 锁相环结构框图

3 永磁同步电机无位置控制的仿真模型与实验结果分析

建立了控制系统模型进行仿真分析，并以TI公司TMS320F2812作为控制芯片进行实物系统搭建，控制系统整体结构如图4所示。仿真设置的电机参数如表1所示。

表1电机参数的设置

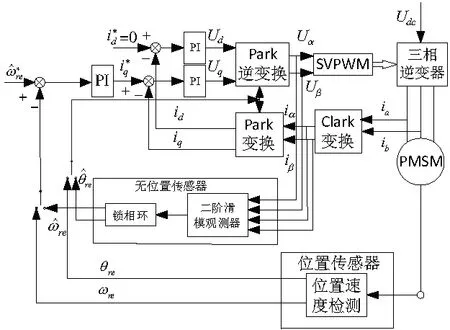
图4 控制系统整体结构

图5是传统滑模观测器与改进后的滑模观测器的仿真对比结果。图6为电机反电势波形仿真对比。图7是电机转子位置估计仿真，图8为电机转速估计仿真。图9是电机给定转速从200r/min增加至500r/min时两种滑模观测器电机转速估计值与实际测量值对比实验结果；图10为电机给定转速500r/min稳态运行过程中，两种滑模观测器转子位置估计值与实际转子位置对比曲线。

(a)传统观测器定子电流

(b)新型观测器定子电流图5 传统观测器与改进后的观测器的定子电流波形仿真对比

(a)传统滑膜观测器估计的反电势波形

(b)新型滑膜观测器估计的反电势波形图6 传统观测器与改进后的观测器的估计反电势波形仿真对比

(a)传统观测器转子位置估计

(b)新型观测器转子位置估计图7 传统观测器与改进后的观测器电机转子位置仿真对比

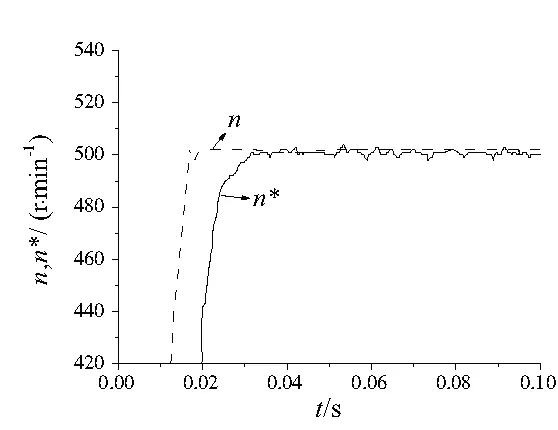
(a)传统观测器速度估计

(b)新型观测器速度估计图8 传统观测器与改进后的观测器电机速度估计仿真对比

(a)传统观测器转子位置估计

(b)新型观测器转子位置估计图9 常规观测器与新型观测器转子位置估计实验波形

(a)传统观测器速度估计

(b)新型观测器速度估计图10 常规观测器与新型观测器电机速度估计实验波形

根据上述仿真对比结果可以得到如下结论:

(1) 图5为突加负载时传统观测器与新型观测器下控制系统的三相定子电流波形，从图5b中可以看出，在0.15s左右新型观测器的定子电流过度比图5a中常规观测器更加平稳，当系统稳定运行时，可以实现

电流波形的正弦化。

(2)从图6中传统观测器与改进后观测器的电机反电动势波形看出，传统滑模观测器反电动势波形中存在严重的“抖振”和高频干扰信号；但是改进后的滑模观测器能够解决滑模中存在的“抖振”问题。

(3)从图7和图9可以得出传统滑模观测器估计的转子位置较实际转子位置稍微滞后一些，两者之间有一定的误差；而新型滑模观测器将混合非奇异终端滑模面应用到传统的线性滑模面上，避免因使用低通滤波引起的相位滞后问题，实现了快速跟踪实际转子位置，使得稳态误差减小。

(4)从图8和图10可以得出传统滑模观测器转速估计波动很大，精度相对较低；而新型观测器由于将锁相功能的转子位置跟踪算法应用到二阶滑模中，使得估计转速的波动减小，精度更加准确，稳态性也得到改善。

4 结论

本文在分析传统的滑模观测器的基础上，提出了一种新型二阶滑模观测器。通过在传统线性滑模面基础上引入了混合非奇异终端滑模面，同时设计了滑模控制律，简化了传统滑模观测器，减少了滤波环节和相位补偿环节，确保了观测器的稳定并有效抑制滑模固有的抖振现象。同时采用李雅普诺夫稳定性理论对所设计的滑模观测器进行稳定性分析，得到电动机转速估算表达式，避免了扩展反电动势的观测。仿真分析和试验研究结果表明设计的滑模观测器，实现了对永磁同步电机的位置和速度的较高精度的估计。

[1] 崔雪萌.内置切向式永磁同步发电机电磁设计及分析[D].哈尔滨：哈尔滨理工大学，2015.

[2] 杨奔,刘景林,卫丽超.基于优化的滑模观测器永磁同步电机无位置传感器控制研究[J].微电机,2015(11): 52-57.

[3] 郭孔辉,纪云峰,庄晔,等.分布式驱动电动车降阶滑模状态观测器设计[J]. 科学技术与工程,2014(20): 121-125.

[4] Chen M S, Hwang Y R, Tomizuka M. A state-dependent boundarylayer design for sliding Automatic Control[J].IEEE Transactions on Automatic Control, 2002, 47(10): 1677-1681.

[5] 姬亚飞.基于滑模观测器的永磁同步电机无传感器速度估计的研究[D].天津:天津大学，2011 .

[6] Ha Q P，Nguyen Q H，Rye D C, et al. Fuzzy sliding-mode controllers with applications[J].IEEE Transactions on IndustrialElectronics, 2001, 48(1): 38-41.

[7] Shyu h h, Lai C h, Tsai Y W, et al. A newly robust controller design for the position control of permanent-magnet synchronous motor[J].IEEE Transaction on Industrial Electronics, 2002, 49(3): 558-565.

[8] Lai C h, Shyu IL h. A novel motor drive design for incremental motion system via sliding-mode control method[J]. IEEE Transaction on Industrial Electronics, 2005, 52(2): 499-507.

[9] Wai R J. Total sliding-mode controller for PM synchronous servo motor drive using recurrent fuzzy neural nettvor [J].IEEE Transactions on Industrial Electronics, 2001, 48(5): 926-944.

[10] 张希，陈宗祥，潘俊民.水磁直线同步电机的固定边界层滑模控制[J].中国电机工程学报,2006, 26(22): 115-121.