基于扩展任务的双臂机器人位姿优化*
2018-01-29房灵申赵明扬朱思俊
郭 鹏,房灵申,赵明扬,朱思俊
(1.中国科学院沈阳自动化研究所 机器人学国家重点实验室,沈阳 110016;2.中国科学院沈阳自动化研究所 扬州工程技术研究中心,江苏 扬州 225127;3.中国科学院大学,北京 100049)
0 引言
随着工业生产系统对机器人工作站的灵活性和自动化程度的要求不断提高,双臂系统作为一种更先进的自动化系统,渐渐成为了学术和工业界的热点研究问题[1]。
在机器人学领域,利用冗余机械臂的特性结合特定的机器人性能指标[15]来提高其在执行任务过程中的灵活性需要用户自己设计或修改机器人的逆解算法[2-3],但是一般来说,大多数工业机器人厂商并不提供给用户修改权限,所以在不修改机器人逆解算法的前提下进行位姿优化成为一个必要的研究课题,Maria等在文献[4]首先提出一种通用的冗余机械臂的位姿优化方法并给出了详细的证明,该方法能够将用户自己选择的机器人性能指标作为优化目标,实现冗余机械臂的位姿优化,在任务冗余的喷涂[5]和钻孔操作[6]这两种案例下已得到验证,它们选用的优化指标分别为单臂动力学可操作性度和单臂运动学可操作度。由于双机器人系统在执行一些协调操作任务时的也可认为是冗余机器人,故也可以利用该通用方法对其进行位姿优化,文献[7]即是采用双臂机器人运动学可操作度作为优化指标一使用双臂系统的相对雅克比矩阵来构造。
本文的主要研究内容是将文献[7]的优化目标进行更改,利用基于各向同性指标[8]对双工业机械臂系统进行位姿优化。为了最大程度地接近实际情况,采用成熟的机器人逆解算法,故利用ABB RobotStudio软件进行仿真。
1 主从双臂机器人的运动学及优化问题描述
在 ABB公司开发的RobotStudio机器人仿真环境中,使用两台ABB IRB140型号的工业机械臂,它们的DH参数如表1所示。
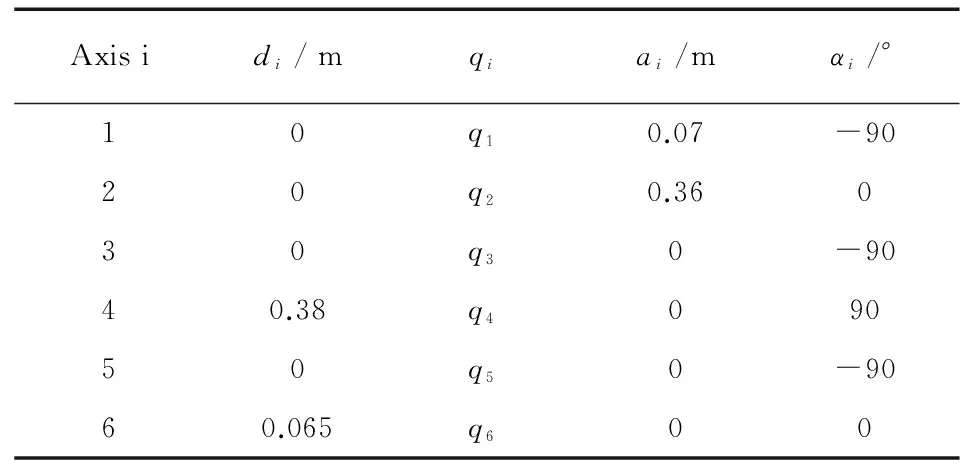
表1 ABB机器人DH参数
1.1 主从双臂系统的运动学
双臂机器人出现冗余特性的一个情形为:用户在描述一个双机械臂协调操作任务时,只对两机械臂末端坐标系的相对位置和姿态作出规定,而对单个机械臂的末端的位姿信息不作约束限定。
为了建立双臂机器人系统的运动学模型,将单臂关节空间扩展为包含两只机械臂的关节空间表达式:
(1)
图1表示了主从机械臂系统的运动链,令W∈SE(3)和T∈SE(3)分别表示主机械臂和从机械臂在某一瞬时的位姿,协调操作任务可以认为是从机械臂相对于主机械臂的位姿变化,所以定义R=W-1T(R∈SE(3))来描述相对运动。当主机械臂的运动和从机械臂相对于主机械臂的运动被确定之后,双臂系统的运动即被完整地描述出来了,如式(2)和式(3)所示:
(2)
(3)
其中,x表示从机械臂相对于主机械臂的相对位姿描述,y表示主机械臂的位姿描述,其中下标r表示相对(relative),l表示主动(leader),ρ,θ,φ分别表示三个欧拉角(ZYZ),f(q)和h(q)表示相对运动和主机械臂的正向运动学表达式。
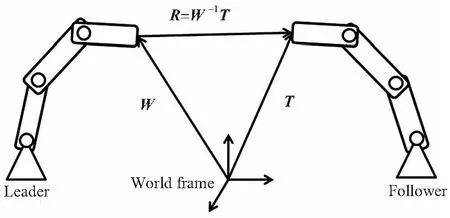
图1 双臂系统的运动链示意图
1.2 通用位姿优化方法的问题描述
如上所述,如果双臂系统在完成协调操作任务时只需考虑两机械臂的相对运动x,而对主机械臂和从机械臂的位置不作约束,此时,由于主机械臂的位置和姿态对协调操作任务没有影响,所以可以任意设置,这就出现了冗余的情形。文献[2]提出的通用优化方法本质上将主机械臂的位姿(y)作为扩展任务,通过约束它来实现对两只手臂的位姿优化。
现设μ(q)为可微的目标优化函数,N为任务雅克比矩阵的零空间的一个基,所以优化问题的数学描述为下式:
minμ(q) subject tox-f(q)=0
(4)
通过简单证明[10]可得(4)式的解为:
(5)
由已知的冗余机械臂逆运动学算法技术可知,如果用户想要优化目标函数μ(q),就需要修改或重新设计机器人逆运动学算法。目前大部分的工业机器人厂商并不会开放给用户足够的权限来修改其控制器内部的算法。所以本文利用这种在不修改和重新设计逆运动学算法[2]的前提下来对双臂机器人系统的位姿进行优化。
文献[2]中提出并证明的基于扩展任务的位姿优化方法可简述为:设n为机器人系统的自由度的数目,k为任务空间的维度,在一个可使任务雅克比矩阵Js非奇异的区域,且存在一个可微的函数h(·):Rn→Rn-k,令增广矩阵JA[3,9]:
(6)
是非奇异的。设σ(q)=0为一个在机械臂运动过程中需要强化的可积分的约束。那么总存在一个可微的函数p(·):Rk→Rn-k,使逆解算法(7)可以求得对约束σ(q)=0强化的解。
(7)
需要指出的是,上述方法表面上使用的仍然是增广雅克比矩阵,但是经过证明也可以使用任何逆运动学算法,例如经典的转置雅克比矩阵甚至是封闭的解析解[2-4]。
图2表示通用姿态优化方法的总体框架图,其中指令x为用户输入到机器人逆运动学算法的任务指令,而扩展任务指令y依赖变量x,由y=-p(x)求得。
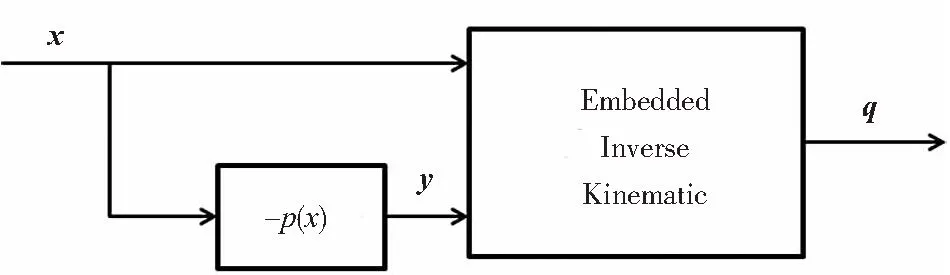
图2 冗余系统的求解框图
优化目标函数μ(q)的选取决定了双臂系统在执行任务过程中体现的运动性能。机器人运动灵活性指标可以量化地表示机器人灵活性和位形的优劣,不同的灵巧性指标针对不同的机器人的性能。经典的灵巧性能指标有可操作度和条件数两种,条件数反映了机械臂末端的速度转化能力的“均匀性”,条件数越小,反映了机械臂末端向操作空间各个方向的速度转化能力分布越均匀[15]。
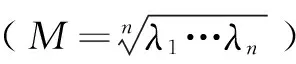
研究表明,将两个机械臂的指标相乘得到的新指标可兼顾到两只机械臂的运动性能[10]。对于工业机械臂的构型来说,前三个关节对整体的机械臂系统的运动灵巧性起到决定性的作用,故在确定优化目标函数的时候,只考虑两只机械臂的前三个关节,如式(8)所示,下称“双臂机器人各向同性指标(DAIM)”。
(8)
将式(8)代入式(5)中可将目标优化函数转化为可积约束,再使用函数拟合的方法求出y=-p(x),最后按照如图3所示的运动学结构对机器人进行编程,就可以达到使用现有的工业机器人的控制器(ABB自带的逆解算法)来优化用户所要求的性能指标(双臂机器人各向同性指标)的目的。这种编程方式与普通的工业机器人编程不同之处是,在确定主机械臂位姿指令的时候调用了函数-p(x)。
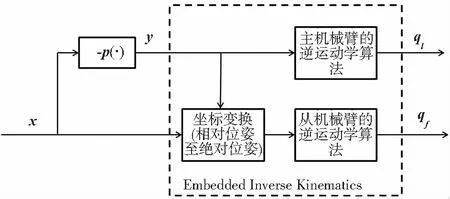
图3 双工业机械臂系统的控制结构框图
2 基于蒙特卡洛方法采样关节值
由于无法以解析方法求得方程-p(x)的表达式,故利用方程拟合的方式来求解,具体步骤为:
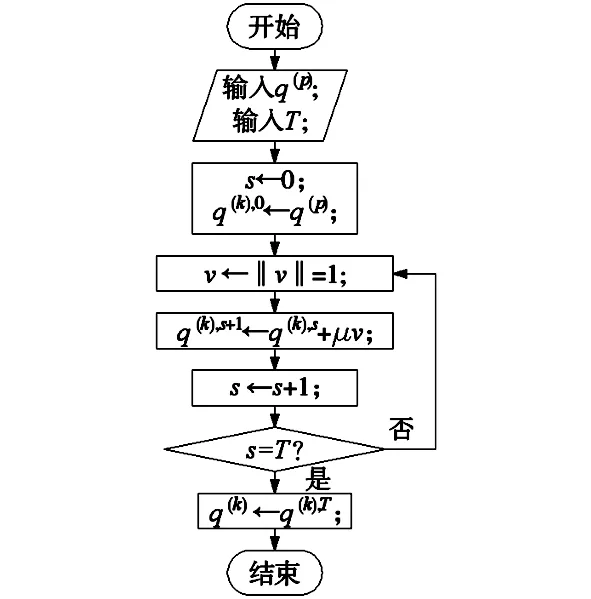
(1)利用蒙特卡洛方法采样出流形σ(q)=0附近的关节值序列q。本文使用与文献[2-5]相同的采样算法,见下述的Hit-and-Run算法及图4和图5所示。
(2)将采样得到的q值代入式(2),式(3)中求解两机械臂的相对位姿值x和主机械臂的位姿值y。
(3)将函数的非线性拟合转化为最小二乘问题,利用优化算法如贪心算法来进行求解。
设预先选定的函数模型序列和系数序列分别为式(9)和式(10),函数p(x) 的求解问题最终可以转化为式(11)所示。
(9)
(10)
(11)
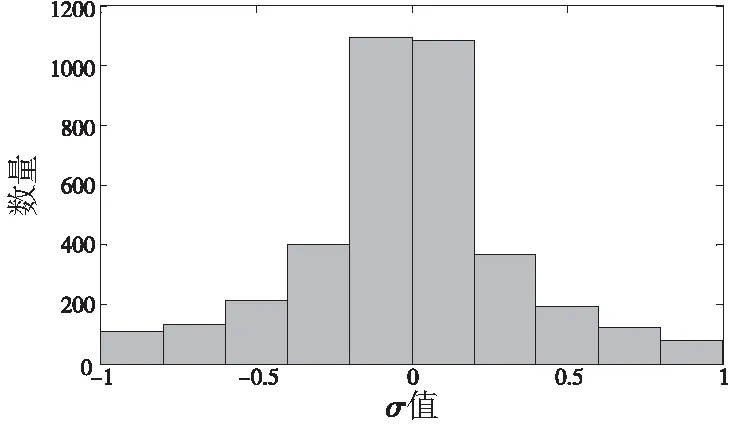
首先,在数学软件Matlab编写采样程序,采样足够多的关节空间q值序列,利用改进的Hit-and-Run[5-8,13]算法在流形σ(q)=0邻域生成一个伪均匀分布D={|σ(q)|<ε},如图5所示,该图表示了采样算法在生成关节点的过程的示意图。
Hit-and-Run伪代码如下所示:
假设已经采样得到k-1 step1:选择跳转次数T≫1; step2:设q(p)为在已经生成的(p=1,…,k-1)个q值中任意挑选的一个值,并将其作为起点; step3:设s←0,q(k),0←q(p); step4:生成一个随机方向v,且‖v‖=1。 step5:设现在生成以q(k),s为起点沿方向v生成下一个点q(k),s+1=q(k),s+μv(经过多次试验μ=2较合适); step6:设s←s+1; step7:若s=T,设q(k)←q(k),T,否则回到step4; step8:returnq(k); 上述的伪代码可用图4的流程图表示。 图4 Hit-and-Run 算法的流程图 图5 Hit-and-Run算法示意图(T=4) 图6 σ 值的分布 根据上节叙述的求解步骤,第2步骤为利用采样得到的关节空间求出x,y。之后第3步骤为对扩展任务y与x的关系进行拟合,即求式(9)和式(11)的向量,最终确定式y=-p(x)。 挑选合适的模型函数,可以快速拟合并提高精度,研究表明将改进的傅里叶序列作为模型函数[14],可以达到快速拟合的效果,表2和表3列举了选择的模型函数(式(9))。利用综合优化分析软件1stopt,调用麦夸特算法(Leverberg -Marquardt)求解,以位移2mm 角度6°为收敛判断标准,确定式(10)表示的系数和常数项c′,最终可求得函数的形式: 表2 主机械臂位置的模型函数 表3 主机械臂姿态的模型函数 表4 系数值结果 RobotStudio是ABB公司开发的具有强大功能的机器人仿真环境,它提供了同ABB机器人实体产品相同的逆解算法。在RobotStudio环境中建立双工业机械臂工作站,利用提供的虚拟示教器结合上述扩展任务拟合公式进行编程。现设定双臂协作任务算例:从机械臂末端沿主臂末端Z轴直线运动(0~100mm)。如式(2)所示,x表示从机械臂(follower)相对于主机械臂(leader)的位置和姿态,在任务路径中共插值5个点即: 对机械臂进行编程。 从机械臂(follower)的程序摘要为: …… MoveJ x1……Wobj:=Leader; MoveJ x2……Wobj:=Leader; MoveJ x3……Wobj:=Leader; MoveJ x4……Wobj:=Leader; MoveJ x5……Wobj:=Leader; …… 主机械臂(leader)的程序摘要为: …… MoveJ func(x1)……; MoveJ func(x2)……; MoveJ func(x3)……; MoveJ func(x4)……; MoveJ func(x5)……; …… 上述从机械臂的指令中: (1)MoveJxi:表示将机械臂的末端移至xi变量所表示的位置和姿态; (2)变量xi:表示双臂协作任务描述的中间路径点。如上述,所设的算例为相对线性运动,现在在路径中都插值5个中间路径点(x1-x5); (3)Wobj:= Leader:表示机械臂末端的参考坐标系为主机械臂的末端。 (4)func()表示函数y=-p(x)。 程序运行时的机械臂的运行过程如图7所示,它们显示了双臂系统在利用了扩展任务的拟合公式(y=-p(x))对机器人编程后的位形随时间的变化过程。首先设置两只机械臂的初始位置(t=0s)为操作性能较劣的位形,随着时间的进行,两只机械臂沿着xi路径点指示的位姿运动,调用的是ABB机械臂自带的逆解算法。 图7 双臂系统执行相对直线任务时运行的位形随时间变化 对于工业机械臂的构型,使其在工作中远离肘关节奇点和肩关节奇点[11],具有很重要的现实意义,它是机械臂能够灵活运动的一个重要因素。观察图7仅从外形的视角可以看出,基于扩展任务关系对机器人编程可使两机械臂都远离两种奇异位形,这体现出了双臂各向同性指标的优化效果和拟合公式的有效性。 图7仅是从外形的角度上观察机械臂的位形。如1.2节所述机器人性能指标(如可操作度、条件数、各向同性指标等)的一个重要功能是可以量化地表示机械臂的操作性能。图7和图8绘制的曲线图表示了双臂的性能指标的值随时间的变化过程。 图8绘制的是本文所选用的优化项“双臂各向同性指标(DAIM)”的值随时间的变化情况,可以看出该值在双臂系统运行时相对初始位置(t=0s)会变大,这说明基于扩展任务的优化方法可以优化DAIM指标的数值。 为了进一步验证两只机械臂确实均处于“速度分布均匀”的位形,现绘制两只机械臂的经典性能指标—条件数—随时间的变化情况如图9所示,可以看出两只机械臂的条件数均会出现变小的趋势,这印证了“双臂各向同性指标”的优化效果同条件数是类似的。 图8 双臂各向同性值随时间的变化 图9 两只机械臂条件数随时间的变化 本文对最近提出的一种通用冗余机械臂位姿优化方法进行了扩展研究,改变了优化指标,将乘积形式的“双臂各向同性指标”作为优化目标,然后对优化问题进行了数学描述,编写采样算法,得到大量的关节空间值的样本,最终拟合出扩展任务(主机械臂的位姿)和相对位姿的数学关系式,利用该关系式在仿真环境RobotStudio对双臂系统进行编程,观察双臂的运行时的位形变化,为了量化显示位形的优化,绘制了性能指标的数值随时间的变化情况。 结果表明: (1)将各向同性指标作为优化项后,基于蒙特卡洛的采样算法对优化函数采样能够在最优位姿附近得到大量的有效的关节值。 (2)根据扩展任务关系式对机器人编程会使两只机械臂在运行的过程中都处于远离轴关节奇点和肩关节奇点,DAIM的值会有增大趋势,条件数的值会有减 小,这显示了本文使用的基于扩展任务的位姿优化方法结合“双臂各向同性指标”的优化效果的有效性。 [1] Smith C. Dual arm manipulation-A survey[J]. Robotics and Autonomous Systems, 2012,60(10):1340-1353. [2] Jamisola R S, R G Roberts. A more compact expression of relative Jacobian based on individual manipulator Jacobians[J]. Robotics and Autonomous Systems, 2015,63: 158-164. [3] Baillieul. J. Kinematic programming alternatives for redundant manipulators. in Proceedings[C]. IEEE International Conference on Robotics and Automation,Boston: IEEE, 1985: 25-28. [4] Zanchettin A M, P Rocco. A General User-Oriented Framework for Holonomic Redundancy Resolution in Robotic Manipulators Using Task Augmentation[J]. IEEE Transactions on Robotics, 2012,28(2): 514-521. [5] Zanchettin A M. Exploiting task redundancy in industrial manipulators during drilling operations[C].IEEE International Conference on Robotics and Automation(ICRA). Shanghai: IEEE, 2011: 128-133. [6] Zanchettin A. On the Use of Functional Redundancy in Industrial Robotic Manipulators for Optimal Spray Painting[C]. IFAC World Congress 2011. Milano, Italy,2011: 11495-11500. [7] Zanchettin A M, P Rocco. Dual-arm redundancy resolution based on null-space dynamically-scaled posture optimization[C].IEEE International Conference on Robotics and Automation (ICRA) SaintPaul: IEEE, 2012:311-316. [8] Jin-Oh Kim,P K Khosla. Dexterity measures for design and control of manipulators[J]. IEEE International Workshop on Intelligent Robots and Systems,1991(2):759-763. [9] O Egeland.Task-space tracking with redundant manipulator[J].IEEE journal on robotic and automation, 2003,3: 471-475. [10] Seraji H. Kinematic functions for redundancy resolution using configuration control[P]. US Patent: 5294873,1994-03-15. [11] 梁新荣. 机器人协调控制及其关节结构优化[J]. 五邑大学学报(自然科学版), 1999,13(1): 42-48. [12] Siciliano.Robotics: Modelling, Planning and Control[M]. London: Springer, 2009. [13] M Chen , B Schmeiser.General hit-and-run Monte Carlo sampling for evaluating multidimensional integrals[J]. Operations Research Letters,1996,19(4):161-169. [14] D Huybrechs,S Olver. Rapid function approximation by modified Fourier series[C]. Proceedings of Highly Oscillatory Problems, Cambridge : Cambridge University Press 2009:51-71. [15] 谢碧云, 赵京. 机器人运动灵活性问题研究概述[J].机械科学与技术, 2011,30(8):1386-1393.

3 扩展任务关系式拟合结果


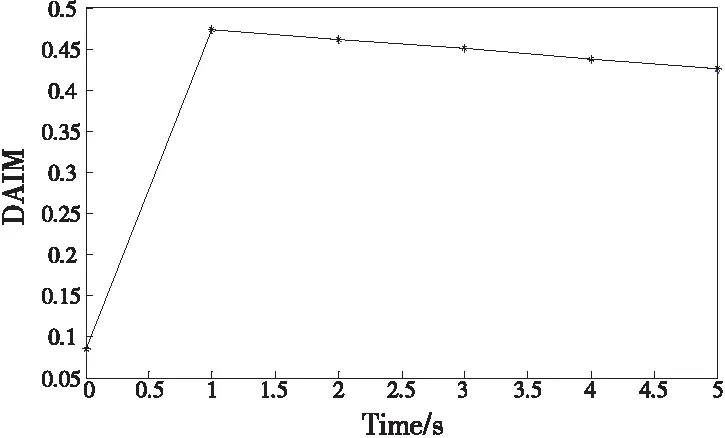
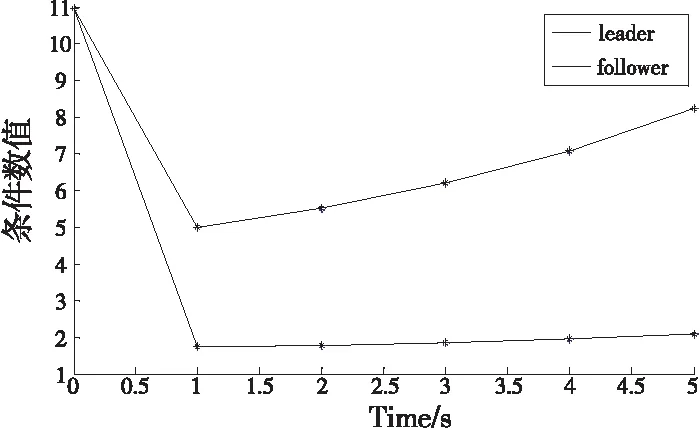
4 基于RobotStudio的仿真结果
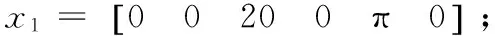

5 结论
