例析高考中的复合最值问题

浙江省金华市第六中学 (321000) 虞 懿

在最值问题中，常常会遇到最大值和最小值相互嵌套在一起的问题，我们称之为复合最值问题．本文采撷几道高考中出现过的复合最值问题并予以深度解析，旨在探索题型规律，归纳求解策略．

策略1数形结合

数形结合是一种重要的数学方法，在处理基本函数的复合最值问题时有广泛的应用，可分别作出几个基本函数的图像，由图像直接求出函数的最值．

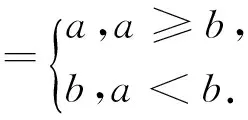
图1

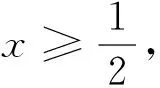
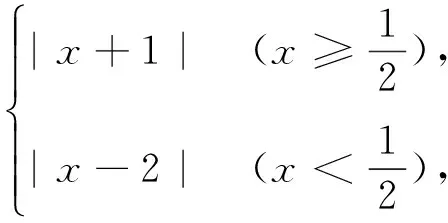
例2 (2009年高考海南、宁夏卷理12)用min{a,b,c}表示a,b,c三个数中的最小值．设f(x)=min{2x,x+2,10-x}(x≥0),则f(x)的最大值为( ).

(A)4 (B)5 (C)6 (D)7

图2

解析：画出y=2x,y=x+2,y=10-x的图像，如图2所示，当0≤x≤2时，f(x)=2x；当2≤x≤4时，f(x)=x+2；当x>4时，f(x)=10-x．所以fmax(x)=f(4)=6，故选C．

例3 (2013年高考辽宁卷理11)已知函数f(x)=x2-2(a+2)x+a2,g(x)=-x2+2(a-2)x-a2+8．设H1(x)=max{f(x),g(x)},H2(x)=

min{f(x),g(x)},(max{p,q}表示p,q中的较大值，min{p,q}表示p,q中的较小值)，记H1(x)的最小值为A,H2(x)的最大值为B,则A-B=( ).

(A)16 (B)-16

(C)a2-2a-16 (D)a2+2a-16

解析：由题意知当f(x)=g(x)时，即x2-2(a+2)x+a2=-x2+2(a-2)x-a2+8，整理得x2-2ax+a2-4=0，所以x=a+2或x=a-2，所以H1(x)=max{f(x),g(x)}=

H2(x)=min{f(x),g(x)}=

结合图形(略)可知，A=H1(x)min=-4a-4,B=H2(x)max=12-4a，则A-B=-16，故选B．

策略2分类讨论

复合最值问题一般包含内外两个层次,当内层关系看不清楚又不宜直接入手时,进行分类讨论是一种行之有效的办法．

例4 (2015年高考浙江卷理18)已知函数f(x)=x2+ax+b(a,b∈R),记M(a,b)是|f(x)|在区间[-1,1]上的最大值．证明：当|a|≥2时，M(a,b)≥2．

当a≥2时，由f(1)-f(-1)=2a≥4，得max{f(1),f(-1)}≥2，M(a,b)≥2；当a≤-2时，由f(-1)-f(1)=-2a≥4，得max{f(-1),

-f(1)}≥2，M(a,b)≥2.

综上，当|a|≥2时，M(a,b)≥2．

评注：分类讨论的最大优点在于各个击破，通过分类讨论使得一些本来困难的求解过程变得简洁明了．

例5 (2015年高考湖北卷文17)a为实数，函数f(x)=|x2-ax|在区间[0,1]上的最大值记为g(a)．当a= 时，g(a)的值最小．

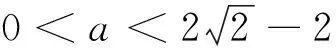
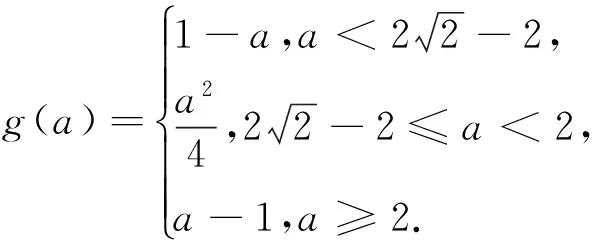
评注：将含绝对值的二次函数在区间上的最值问题和分段函数的最值问题融合在一起，运用分类讨论的思想将含绝对值问题转化为分段函数的问题，充分体现了分类讨论和化归转化的数学思想，能较好地考查知识综合能力.其解题的关键是运用分类讨论求出g(a)的表达式和分段函数在区间上的最值求法.

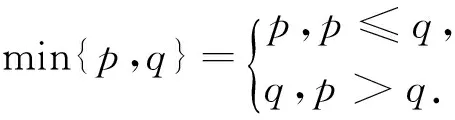
解析：(Ⅱ)(ⅰ)设函数f(x)=2|x-1|，g(x)=x2-2ax+4a-2，则f(x)min=f(1)=0，g(x)min=g(a)=-a2+4a-2，所以，由F(x)的定义知m(a)=min{f(1),g(a)}，即

(ⅱ)当0≤x≤2时，F(x)≤f(x)≤max{f(0),f(2)}=2=F(2)；当2≤x≤6时，F(x)≤g(x)≤max{g(2),g(6)}=max{2,34-8a}=max{F(2),F(6)}．

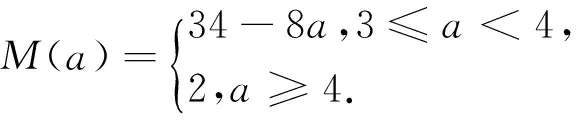
评析：(Ⅱ)(ⅰ)先求函数f(x)=2|x-1|，g(x)=x2-2ax+4a-2的最小值，再根据F(x)的定义可得F(x)的最小值m(a)；(ⅱ)分别对0≤x≤2和2≤x≤6两种情况讨论F(x)的最大值，进而可得F(x)在区间[0,6]上的最大值M(a)．

后记：高考数学试题在解题方法上强调“通性通法”，这也是近些年高考数学命题的重要出发点．具体表现为数学解题方法的常规化和大众化，数学解题方法避开生僻的解题技巧和独门技巧，提倡通性通法的解题理念．高考数学试题的解题方法多种多样，以“通法”为主，既包括了常规的解题思路又囊括了精妙简单的解题方法．可以通过对高考试题解题方法的研究来逐步培养学生在数学领域的学习兴趣，提高学生的数学解题能力．