用叠加模式将数学史融入数学教学——以“一元二次方程求解”为例

南京师范大学教师教育学院 (210024) 朱大龙

以HPM视角来进行数学教材设计和课堂教学，日益受到教育界关注.近期在德国汉堡大学举行的第十三届国际数学教育大会中第25个研究专题强调，要认识数学史在数学课堂和教学中的作用[1].

根据汪晓勤教授的划分，数学史融入到数学教学的方式主要可分为四种“附加式”、“复制式”、“顺应式”、“重构式”.“附加式”是指在教学中，介绍数学故事，数学家图片或介绍数学符号、概念的来源的方法. 其可以使教学更加有趣、生动，但过于浅显，不能挖出知识的内涵. “重构式”是指在教学中借鉴或重构知识的发生，发展的历史，采用发生法进行教学的方法[2]. 其使教学顺乎知识的发展规律，可以使学生再创造式的学习新知识，但重构难度大，缺少直观性，易使课堂枯燥.现今，我国中学教材对于数学史以历史故事或历史题目为主的“附加式”融入居多，而对于从知识的历史源头，“重构式”这种高层次的融入，明显不足[3].如若将它们结合起来，在“附加式”中融入“重构式”，必然会使教学更优化.本文以一元二次方程求解教学片断及分析为例，探讨“附加-重构”叠加模式的运用.

1.西方一元二次方程的解的发展史

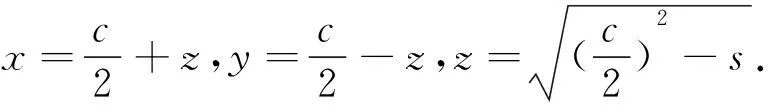
2.教学片段及分析

2.1教学片断 1 由史引入，数形结合

师：在古巴比伦这个国家，当时很多人认为一块长方形的田的面积只与它的周长有关，于是有一些商人就靠农民认知的错误来占农民的便宜，比如他们把4×6的一块田来当成2×8的价格来买，当时的书记员想办法解决这个问题[5].

师：长方形面积和什么有关？

生(全体)：长和宽.

师：正方形的面积呢？

生(全体)：一边的长(也有人回答周长).

师：怎么能使面积由周长确定了呢？

生1：把它变成正方形.

教学片断分析:“附加式”的情境设置.情境是知识赖以产生意义的背景，是认知学习的来源，通过数学史设置情境，能让学生体会到原汁原味的数学文化.从相对轻松的历史趣事上开始一节课的内容，在一节课的开始便能吸引学生的注意力；让学生融入到历史情境中，激发学生探索发现的兴趣；但学生还不能一下子找出问题的解决方法，教师要根据学生的认知规律和历史发展，设置问题，由浅入深、由表及里，引导学生将现实的历史故事抽象成几何图形问题，再将几何图形联系到一元二次方程，自然而然的在数与形中发现求解方法.为重构搭建起数学史的桥梁.

2.2 教学片断2 化长为方，由形得解

师：长方形长y米，宽x米，长宽之差为2米，面积为15平方米，(在黑板上画出图形)，是否可以写出哪些方程？

生2：y-x=2,xy=15.

生3：可化成一元二次方程(x+2)·x=15.

师：画出图1.根据图形怎么可以化长为方？

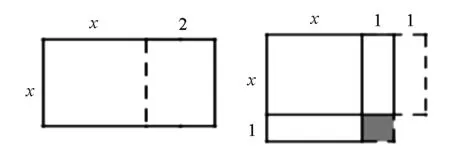
图1 图2

生4：可以用割补法(得到图2).

师：割补后的正方形面积怎么表示？

生5：(x+1)2.

师：用等式表示正方形面积和长方形面积的关系？

生(全体)：(x+1)2=15+12.

师：仔细观察这个方程，有什么发现？

生6：可以用直接开方法解出x.

生7：得出(x+2)·x=15的解.

教学片断分析:承接“附加式”的情境进行重构.学生学习配方法解方程，最困难的地方是如何设计教学，再现配方法的发现过程.此教学片断通过设疑，问答的方式，引导学生发现解法.避免了传统教学直接给出方程，让学生探究如何解方程，这种脱离历史和生活的教学方法.而是让学生在解决化长为方的历史问题中，偶然地得出了方程的解.从而引发思考是如何得到的解，回头重视整个过程，发现一元二次方程可以表示成长方形，进而通过割补得到一个完全平方公式，得出解.在数学史的发展中，很多理论的发现恰恰是偶然的，而让学生经历这种偶然，从而进行思考总结自己的这个偶然发现，恰恰是当今教学中需要的重构学习的一种方式.

2.3 教学片断 3 类比探究，由形归数

师：观察求解过程，有什么发现？是否有更简单的方法？(板书出过程，如下).

x2+2x-15=0⟹(x+2)·x=15⟹(x+1)2=15+12⟹x2+2x+12=15+12.

生8：与原方程相比，等号两边加上了小正方形的面积，凑成了完全平方的形式.

师：是否可以得出一般的求解方法.

生9：首先将常数移到等式右边，然后等式两边各加上一次项系数一半的平方，等式左边可化成完全平方，最后直接开平方求出x.

教学片断分析:反思重构过程，总结升华.最初的偶然的发现往往是不够完美的，在经过最初发现的惊喜过后，要做的便是回顾、验证、分析、总结，进一步完善自己的发现.在学生通过化长为方发现求方程的解，经过短暂的兴奋，喜悦之后，教师通过引导，激发学生进一步思考，分析，对比之前求解的思路，让学生最终发现简便，一般的求解方法.

3叠加模式解析

数学史融入数学教学是个综合的过程，需要发掘出丰富的数学史料，而后将其融入教材，最后再由教师进行加工运用到教学中.其中如何发掘更多史料，如何将数学史融入教材需要数学史专家、数学教育专家、教材编写人员通过不断的探索，实践来获得，这是一个漫长的过程.但让教师运用和加工现有的史料和教材，如上案例中，使数学史“附加-重构”叠加式融入教学中，可以找到一个普遍的教学设计步骤.

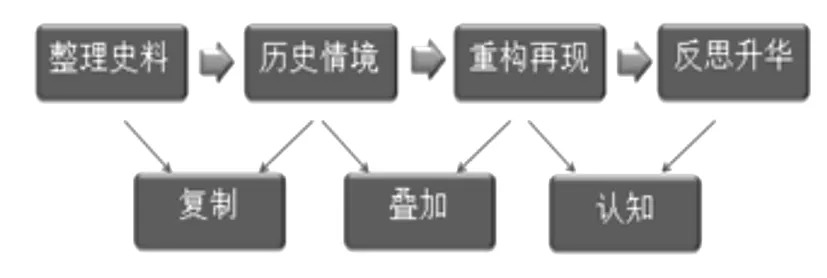
图3

整理史料：在对某一个知识的讲解，你希望融入数学史时，你需要大量搜索与它有关的历史资料，不能仅仅满足教材上提供的一些历史资料.在材料的选取上需要做到两点：1、思考你需要设置什么样的情境，哪些材料具有代表性适合放入情境中.之后在相关历史材料中，提炼出对你符合要求的历史材料，为情境设置做准备；2、明确知识是如何产生发展的.整理出一条主 “脉络”，为重构做准备.

历史情境：以数学史料创设的情境，就是呈现给学生刺激性数学历史，引起学生学习数学的兴趣，感受数学的文化，激起学生的好奇心、发现欲，产生认知冲突，诱发质疑猜想，唤醒强烈的问题意识，从而使其发现和提出数学问题，解决数学问题[5]．利用已整理好的史料，根据课程需要达到的效果，直接引用或适当改编史料，设置一个有历史，有故事，有启发的情境为重构做准备.故事情境是为了文化的显性表现，重构则是为了文化的隐性再创造.

重构再现：根据情境中产生的问题，引导学生按照整理史料环节所制定知识的历史 “脉络”(引导的方法可多样化，可通过启发、游戏、实践等方式)重构对于这部分知识的发现过程.上述教学片断中，以通过对古巴比伦的卖田为情境，让学生探讨化长为方的问题，通过教师的巧妙引导，让学生探究求解过程，实现重构.

反思升华：在让学生重现了历史发展的过程后，一定要让学生自己总结在这一过程中发现了什么，怎么发现的，有什么启发.从而发掘出其中的数学思想，体味数学的文化，巩固新建构的认识.

4.反思总结

本节课主要通过附加式和重构式将数学史融入数学教学.整体上看，从由数到形，化长为方；到由形到数，解出方程；最后归纳总结整个过程，再现了解一元二次方程的历史发展过程，属于重构式.从局部看，利用数学史中的一个历史故事作为情境设置，属于附加式.历史故事作为情境，可以让学生再次回到历史创造环境氛围中去，仿佛身临其境.而后为了解决情境中的问题，教师通过设疑，提示，引导学生重回历史发展之路，探索重构一元二次方程的解.

数学史中包含着丰富的教学素材和思想养料，包含着不同时空，各个数学家的探索精神和创新思维[6]，如果全然抛弃这些历史素材，数学课堂就变成了一个“模仿作坊”，学生学习到的只是单调的定理，公式，学到的只是一具数学的躯壳，没有灵魂的数学.自然，学生无法体会到历史中数学家的思维之妙，也不能感受多元文化.“附加-重构”叠加式融入数学史，这一模式，既有“附加”让学生直观体会到数学的历史、文化，又有“重构”让学生再创造式的探索发现知识，体会到数学家们精妙的思想，感受数学的魅力.

[1]徐斌艳.2016年相聚在第十三届国际数学教育大会[J].中学数学月刊，2016，(6):1-3.

[2]汪晓勤.数学史与数学教育[J].教育研究与评论，2014，(1)：8-14.

[3]刘超.人教版初中、高中数学教材中数学史的调查分析[J] .基础教育，2011，(8-2)：99-105.

[4]VICTOR J . KATZ.数学史通论(第二版)[M] .高等教育出版社，1980.28-31.

[5]吕传汉，汪秉彝.再论中小学“数学情境与提出问题”的数学学习[J].数学教育学报，2002，(4)：73-76.

[6]汪晓勤.20世纪中叶以前的正弦定理历史[J].数学通报，2016，(1)：1-5.